电厂燃煤虚拟采样及发热量均值不确定度评定

刘福国 国钦光，殷炳毅，王守恩

(1.国网山东省电力公司电力科学研究院，山东 济南 250003；2.山东电力研究院，山东 济南 250003；3.华电潍坊发电有限公司，山东 潍坊 261000)

1 引 言

检测发电机组效率时，锅炉燃煤发热量还无法连续测量，只能通过采集入炉煤样品，在实验室化验分析得到[1]。用少量样品煤的化验数据表示检测周期内入炉煤发热量，其不确定性来自样品采集和实验室分析等2个环节[2]，采样环节引起的不确定度占95%以上[3]。文献[4]研究了锅炉采样样品煤发热量的概率分布特性，对单个样品发热量的不确定度进行了评定。在实际生产中，机组效率常用供电煤耗表示，电厂日常供电煤耗检测周期有时长达1个月、1个季度甚至1年。检测周期内的燃煤发热量一般采用多个样品煤发热量的平均值[5]。因此，多次采样样品发热量均值的不确定度评定对机组效率检测具有重要意义。

μx=μ

(1)

(2)

当总体N为正态分布或样本容量n>30时，样本均值的抽样分布可作为正态分布，正态分布的参数μx、σx根据式(1)、式(2)计算，故可对n个样品发热量均值的不确定度进行评定。

但当总体N为非正态分布且样本容量n<30时，样本均值的抽样分布为非正态分布，此时，如何对n个样品发热量均值的不确定度进行评定，是本文要解决的问题。

2 虚拟采样及发热量均值不确定度

非正态总体N通常来自实际采样实验，为已知数据。要对n个样品发热量均值的不确定度进行评定，首先获取样本均值的抽样样本，传统方法[9]是从总体的N个发热量中随机抽取一个容量为n的样本，计算该样本均值，采用同样方式进行多次抽样，得到样本均值的抽样样本，利用该样本对均值的不确定度进行评定。从总体的N个发热量中抽取容量为n的样本，重复抽样总计可得到Nn个样本，因此样本均值抽样样本的最大容量为Nn。

获得样本均值的抽样样本的另一种方法是基于蒙特卡洛法[10，11]的随机采样实验，与传统抽样方法相比，随机采样试验获得的虚拟样本容量是任意的，采用随机采样试验对n个样品发热量均值的不确定度进行评定的步骤为：

(1) 计算总体N的发热量概率密度。

(2) 将总体N发热量概率密度表示成多项式函数。

(3) 建立虚拟采样系统。按照总体N的概率密度产生随机数，作为虚拟采样样品的发热量。这种利用给定概率密度函数进行随机样抽的系统，看作是样品发热量的虚拟采样系统。

(4) 利用虚拟采样系统进行n次采样，得到n个虚拟样品的发热量数据，计算发热量的平均值，得到第1个发热量均值；采用同样的方法得到m个发热量均值，作为发热量均值的抽样样本。

(5) 计算发热量均值样本的平均值、标准差及概率密度分布，在给定置信概率下求取包含系数，得到n个样品发热量均值扩展不确定度。

以某电厂锅炉为例，对入炉煤发热量均值不确定度进行评定。

2.1 样本N的获得

表1为某电厂2017年5～7月入炉煤实际采样试验样本N，该样本包含276个样品煤的发热量[12]。这些发热量数据既包含实验室化验分析引起的不确定性，又包含采制样本环节引起的不确定性。研究表明，实验室分析环节引起的不确定度约为0.05 MJ/kg[13～15]，而采制样本环节引起的不确定度为0.5～2.5 MJ/kg[2，4，12]。因此，忽略实验室分析环节的不确定度，可认为表1中发热量数据的不确定性是由采制样本引起的。利用表1的数据对n次采样发热量均值的不确定度进行评定。

表1给出的样本平均值μN=19.686 MJ/kg，标准差σN=0.933 MJ/kg。

表1 总体样本N的发热量Tab.1 Calorific value of sample N MJ/kg

2.2 样本N的概率密度函数

总样本N中，发热量最小值为16.894 MJ/kg，最大值为21.217 MJ/kg。将此区间等分成若干个子区间，统计每个子区间内的样品个数，计算落入区间的概率，概率密度是概率的变化率。利用Matlab统计工具箱中的hist函数可以统计落入每个子区间内的样品数，利用ksdensity函数可以对样本N的概率密度进行核心平滑估计[16]。由图1给出的通过区间统计得到的概率密度的直方图以及概率密度平滑估计可以看出，样本发热量不服从正态分布。概率密度平滑估计结果可用8阶多项式函数f表示为：

图1 总体样本N的概率密度Fig.1 Probability density of population sample N

(3)

对于总体样本N，式(3)所示的多项式函数由分段函数f1和f2组成，在不同区间上，函数f1和f2的系数见表2。

表2 多项式函数f的系数Tab.2 Coefficient of polynomial function f

2.3 虚拟采样

根据概率密度函数式(3)，采用挑选抽样方法产生发热量样本，这种方法由冯·诺依曼在1951年提出[17]。如图2所示，当已知概率密度函数f(Q)时，利用挑选抽样法产生发热量随机数的主要步骤为：

(1) 在发热量取值区间[a，b]内，产生均匀随机数Q。

Q=(b-a)r1+a

(4)

式中：r1为区间[0，1]均匀随机数，r1∈[0，1]。

(2) 在[0，fmax]区间内，产生均匀随机数f。

f=r2fmax

(5)

式中：r2为区间[0，1]均匀随机数，r2∈[0，1]；fmax为函数f(Q)在区间[a，b]上的最大值。

(3) 当f≤f(Q)时，接受Q为所选的随机数，否则，返回第(1)步，重新抽取1对(Q，f)。

根据图2，挑选样抽法的几何解释为：随机选取位于矩形abcd内的点(Q，f)，选择位于曲线f(Q)下面的点，它们对应的发热量Q服从概率密度为f(Q)的分布。

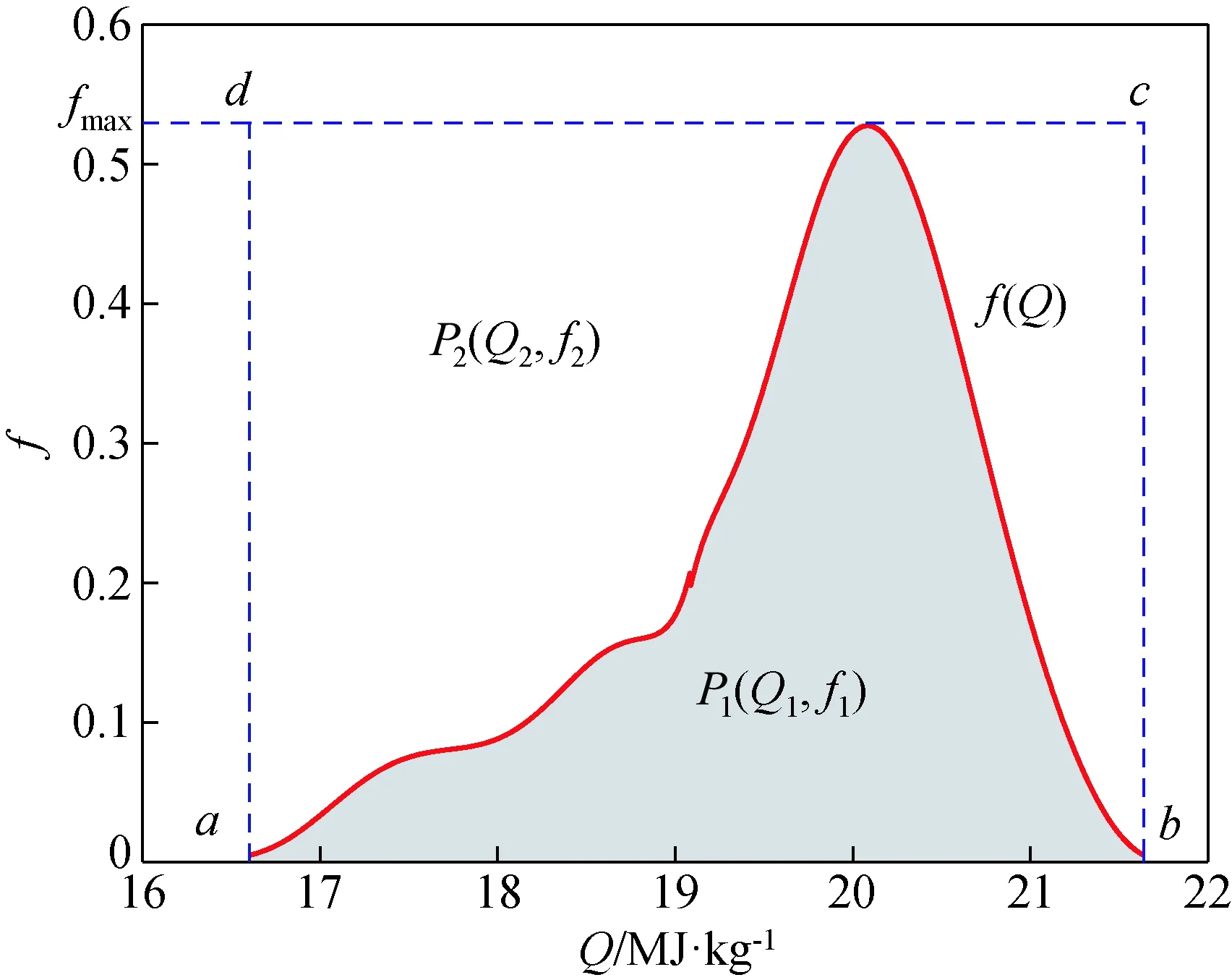
图2 根据给定概率密度函数f(Q)产生随机数QFig.2 Generating random numbers Q based on a given probability density function f(Q)

2.4 均值样本的获得及评定

要对n次采样发热量均值的不确定度进行评定，首先利用第2.3节的虚拟采样技术获得均值样本。按式(3)给定的概率密度函数，产生n个发热量随机数，计算它们的平均值，作为发热量均值的第1个采样数据。用相同方式得到m个发热量均值的采样数据，作为发热量均值样本。

取n=4和n=50，采用虚拟采样方法分别得到发热量均值样本，样本容量m取为m=10 000。对样本进行统计计算，n=4时，样本平均值μ4=19.689 MJ/kg，标准差σ4=0.480 MJ/kg；n=50时，样本平均值μ50=19.689 MJ/kg，标准差σ50=0.135 MJ/kg。利用ksdensity函数对2个样本的概率密度进行核心平滑估计，n=4时，结果见图3，其概率密度可拟合成式(3)所示的多项式函数f(Q)，限于篇幅，这里不再给出多项式系数；n=50时，区间统计得到的概率密度直方图以及函数ksdensity的平滑估计结果见图4，发热量均值样本非常接近正态分布，图4中还给出了正态分布N(19.686，0.1352)的概率密度，可以看出，它和平滑估计结果吻合良好。

图3 n=4时发热量平均值的概率密度分布Fig.3 Probabilistic density distribution of the mean calorific value at n=4

图4 n=50时发热量平均值的概率密度分布与正态分布的对比Fig.4 Comparison of probability density of average calorific value with normal distribution at n=50

如图3，对n=4时发热量均值的不确定度进行评定，就是求给定的置信概率ε下的包含因子k，根据置信概率的定义[18]得到关于包含因子k的方程如式(6)。

求解式(6)，可得到包含因子k。求解时取置信概率ε=0.95，式(6)中μ4=19.689，σ4=0.480。采用迭代法求解式(6)，得到k=1.934。因此，n=4时发热量均值的扩展不确定度为kσ4=0.928 MJ/kg，此时发热量均值结果可表示为19.689±0.928 MJ/kg。

(6)

根据虚拟采样方法，同样可对n=50时发热量均值的不确定度进行评定。利用Matlab的jbtest函数对n=50时发热量均值样本进行正态性检验[19]。结果表明，均值样本服从正态分布，置信概率ε=0.95对应的包含因子k=1.96[20,21]，发热量均值的扩展不确定度为kσ50=0.265 MJ/kg。因此，n=50时发热量均值的采样化验结果可表示为19.689±0.265 MJ/kg。

3 结 论

(1) 在发电机组效率检测时，锅炉燃煤多次采样样品发热量均值的不确定度评定对于机组效率检测具有重要意义。

(2) 已知燃煤发热量样本，要对n个样品发热量均值的不确定度进行评定，当发热量样本正态分布或n>30时，则n个样品发热量均值服从正态分布，该正态分布的参数、根据式(1)和式(2)计算，据此可对n个样品发热量均值的不确定度进行评定。

(3) 当发热量样本不服从正态分布且n<30时，要对n个样品发热量均值的不确定度进行评定，可采用挑选样抽法进行虚拟采样，得到n个样品发热量的均值样本，然后根据该均值样本的概率密度分布对发热量均值的不确定度评定。

(4) 采用虚拟采样均值样本对n个样品发热量均值的不确定度评定结果与根据中心极限定理得到的结论一致。