多重分形去趋势波动分析及改进决策树在电能质量分析中的应用

张淑清，张 赟，刘海涛，胡 皓，李 华， 姚玉永，刘 勇，王 涛

(1.燕山大学 电气工程学院，河北 秦皇岛 066004；2.东北大学 信息科学与工程学院，辽宁 沈阳 110004；3.国网冀北电力有限公司唐山供电公司，河北 唐山 063000)

1 引 言

经济社会的不断发展，各种新型电气设备的使用，产生了大量的非线性负荷和冲击性负荷。这些非线性负载的使用不可避免地造成电网的幅值和频率发生偏差，造成电能质量(power quality)的下降，不仅影响日常生活还会造成巨大的经济损失甚至电力事故。电能质量信号具有非线性和非平稳性的特点。目前电能质量扰动信号的分类识别方法主要为小波变换、S变换、EMD分解、HHT变换等时频域分析法[1～4]。

多重分形去趋势波动分析(multifractal detrended fluctuation analysis,MFDFA)是在DFA基础上提出的一种非线性时间序列的分析方法，可以有效消除干扰趋势，估计多重分形谱[5]。文献[6]采用MFDFA方法对风电厂时间序列进行分析，实验表明风速变化与多重分形参数有一定的关联性，有效判断风速的变化趋势。文献[7]针对非线性的脉冲信号，提出多重分形消除趋势波动分析和PSO-SVM的方法，有效识别了4种脉冲信号。文献[8]提出了基于多重分形降趋波动分析法的谐振接地系统故障选线新判据，仿真结果表明该判据抗噪能力强，计算速度快,克服了消弧线圈和故障条件等因素对故障选线的影响。文献[9]针对齿轮箱故障诊断提出了一种基于多重分形的趋势波动分析和改进的K均值集群的方法。文献[10]针对EEG信号使用MFDFA方法提取了4个特征集，用作支持向量机和k-最近邻分类器的输入，实验证明所提出的MFDFA辅助特征提取方法获得较高的分类精度。目前，MFDFA方法广泛应用于股票交易数据[11]、机械振动信号[12]、电力系统故障选线[13]、人体脑电信号[14]等。

决策树是由一种自上而下的递归算法，广泛应用于数据的预测，挖掘与分类。其核心算法最早是由Quinlan提出的ID3算法。C4.5是在ID3算法的基础上进行的改进，以信息增益率代替ID3算法中的信息增益作为属性选择判断条件[15]。由于计算信息增益率过程中大部分为对数运算，C4.5运算时间长，效率低。基于麦克劳林公式对C4.5算法改进的决策树模型，将计算过程中的对数运算简化，提高了运算效率[16]。

本文提出一种基于MFDFA和麦克劳林公式改进决策树的电能质量分析方法。首先通过分析证明了电能信号具有多重分形特性，然后计算信号的多重分形谱参数，从中选取3个参数(hqmax、αmin、α0)和信号能量E共4个参数作为信号的特征矩阵，最后，通过改进决策树实现对不同类型扰动信号的识别。

通过实验及对比分析验证了MFDFA方法的优越性：首先向信号中添加不同信噪比的白噪声，证明了该方法具有较好的抗噪性；然后与总体平均经验模式分解(ensemble empirical mode decomposition,EEMD)、希尔伯特-黄变换(Hilbert-Huang transform,HHT)和双树复小波变换(dual-tree complex wavelet transform,DTCWT)三种常见特征提取方法[17]进行对比实验，用改进的决策树分别对上述提取的特征向量进行分类识别，结果证明，用本文方法提取的特征向量进行分类其精度优于其它方法。

2 电能质量信号的多重分形特征

2.1 多重分形去趋势波动分析

多重分形去趋势波动分析可以有效消除干扰趋势，估计多重分形谱，多重分形去趋势波动分析思路是：

(1) 设非线性时间序列信号xk，构造信号的离散时间序列Yi：

(1)

(2) 将时间序列Yi划分为互不重叠的N个小区间，每个小区间包含s个数据。考虑到Yi的长度N不一定整除s，造成剩余一段数据剩余，因此再次从数据的反方向以相同的长度s将时间序列分成互不重叠的N段数据，这样一共得到2N段数据。

(3) 使用最小二乘法拟合法计算每段数据的局部趋势，确定每一段数据的均方误差F2(v,s)：

当v=1,2,…,N时，

(2)

当v=N+1,…,2N时，

(3)

式中：yv(i)是第v段数据的拟合多项式，多项式yv(i)的阶数m越大趋势消除的效果越好，相应的计算时间也会相应增加。当m=1，2，3，…时，分别记为mfdfa1，mfdfa2，mfdfa3，…，通常m+2≤s≤N/4。

(4) 设波动函数Fq(s)阶数为q，则：

(4)

一般来说q可以取非零的实数，当q=2时，MFDFA退化成DFA算法。

(5) 如果离散时间序列信号xk存在自相似性，则q阶波动函数Fq(s)和时间尺度s之间满足幂律关系：

Fq(s)∝sh(q)

(5)

式中：h(q)为广义Hurst指数，定义q～h(q)为广义Hurst指数谱，其中：

(6)

h(q)的值随着q值的改变而发生变化时，即q～h(q)表现为非线性函数，则时间序列展现出多重分形特征。

对于离散时间序列的广义Hurst指数h(q)，多重分形理论中的质量指数τ(q)和分形维数D(q)之间满足：

τ(q)=qh(q)-1

(7)

(8)

通过Legendre变换，得到奇异指数α和多重分形谱f(α)：

α=τ(q)′=h(q)+qh(q)′

(9)

f(α)=qα-τ(q)=q[α-h(q)]+1

(10)

多重分形谱宽度Δα=αmax-αmin，反应了整个结构概率分布的不均匀程度，αmax是最大概率子集，αmin是最小概率子集，可以用来描述信号的多重分形强度。分形维数差ΔDq=Dqmax-Dqmin，ΔDq反映了最大波动与最小波动的频率比，Dqmax是最大波动点集的分形维数，Dqmin是最小波动点集的分形维数，ΔDq值的大小表示电能扰动信号中波动最平稳的子集个数与波动最剧烈的子集个数的比例。

2.2 电能质量信号的多重分形特征的发现

本文首先对电压暂降(sag)、电压暂升(swell)、暂态振荡(transient oscillation)、谐波(harmonic)、闪变(flicker)、脉冲(transient pulse)等6种电能质量信号进行多重分形特征分析，证明电能质量信号具有多重分形特征。根据国家标准技术委员会及相关行业标委会制定的电能质量国家标准[18]，6种电能质量信号的扰动模型及具体参数设置如表1所示，信号扰动发生的幅值、起始时间和持续时间由Matlab随机产生。

表1 电能质量扰动模型Tab.1 Power quality disturbance model

根据MFDFA算法的原理可以发现，广义Hurst指数h(q)，质量指数τ(q)，奇异指数α和多重分形谱f(α)四个参数可以描述信号的多重分形特性。

根据式(6)计算广义Hurst指数h(q)，当h(q)的值随着q值的改变而发生变化时，即q～h(q)曲线表现为一个非线性函数，则时间序列展现出多重分形特征。图1给出了的广义Hurst指数，根据广义Hurst理论，当q>0.5时，时间序列时长程相关；当q<0.5时，时间序列时短程相关。从图中可以看出，每一种电能质量信号的h(q)均大于0.5，因此可以确定电能质量信号是一个长程相关的时间序列。

根据MFDFA算法的原理可以发现，广义Hurst指数h(q)，质量指数τ(q)，奇异指数α和多重分形谱f(α)四个参数可以描述信号的多重分形特性。

根据式(6)计算广义Hurst指数h(q)，当h(q)的值随着q值的改变而发生变化时，即q～h(q)曲线表现为一个非线性函数，则时间序列展现出多重分形特征。图1给出了的广义Hurst指数，根据广义Hurst理论，当q>0.5时，时间序列时长程相关；当q<0.5时，时间序列时短程相关。从图中可以看出，每一种电能质量信号的h(q)均大于0.5，因此可以确定电能质量信号是一个长程相关的时间序列。

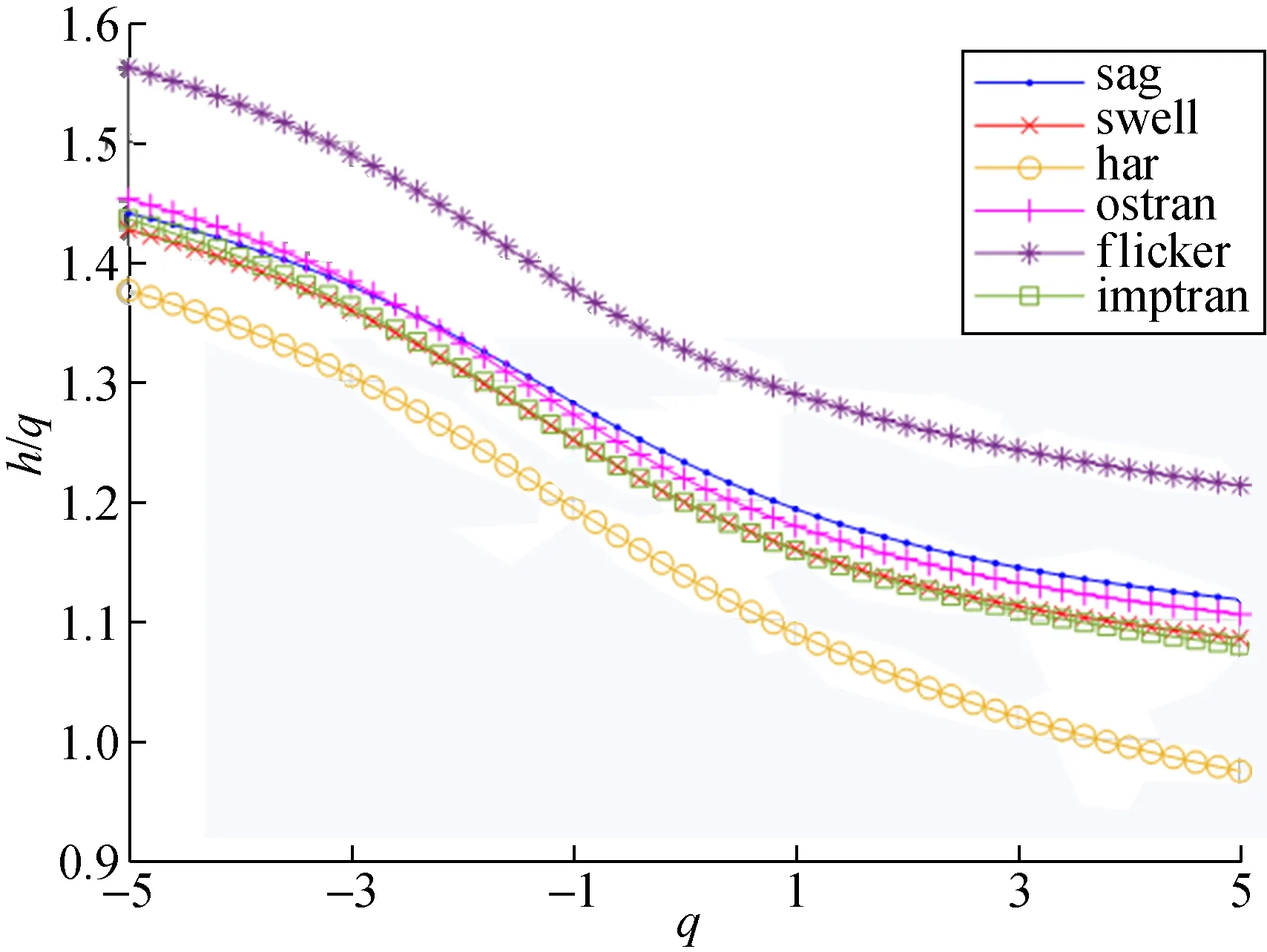
图1 广义Hurst指数h(q)Fig.1 Generalized Hurst index h(q)

根据式(7)计算信号的标度指数τ(q)，判断多重分形特性。当τ(q)为一条直线时，表明信号函数是单分形的，若τ(q)表现出非线性，则表明信号函数是多重分形的。对电能质量信号进行分析，得到τ(q)随q的变化曲线，如图2所示。从图中可看出τ(q)～q之间存在明显的非线性关系，这表明了电能质量信号具有多重分形性质。

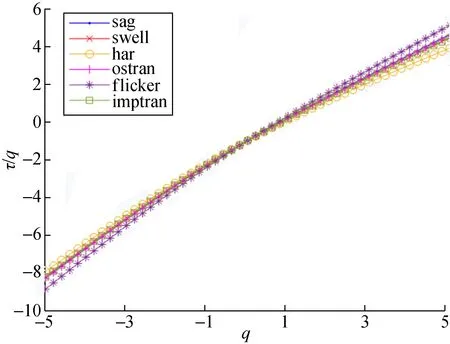
图2 标度指数τ(q)Fig.2 Scale index τ(q)

根据式(9)和式(10)可以得到信号的奇异指数α和多重分形谱f(α)。如果时间序列是多重分形特性的，α～f(α)曲线是一个单峰钟形。图3给出了6种电能质量扰动信号的多重分形谱图，图中曲线反映了奇异指数和分形维数的关系。从图3中，可以明显看出电能信号是具有多重分形特征的。

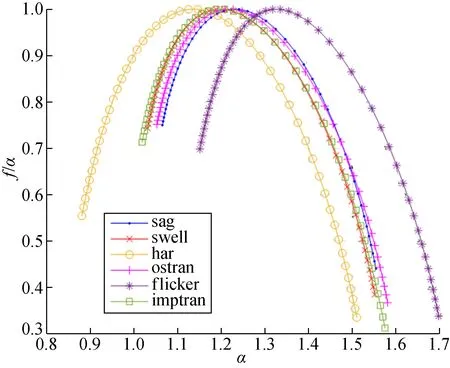
图3 多重分形谱图Fig.3 Multifractal spectrum

3 信号的多重分形特征提取

信号经多重分形分析，计算出4个分形参数Hurst指数h(q)、尺度指数τ(q)，奇异指数α和多重分形谱f(α)，如图1至图3所示。从图中可以看出不同类型的信号间的h(q)、f(α)和α三个参数有着明显区别，可以从中选取能表征信号特征的参数。下面就以电压暂降信号(sag)为例说明基于多重分形参数的特征提取过程。

图4和图5是某一电压暂降信号(sag)的多重分形谱f(α)和Hurst指数h(q)。图4中α～f(α)曲线中3个点是起始点，终止点和最高点，它们对应的奇异指数分别为αmin、αmax、α0。图5中q～h(q)曲线中3个点分别是q=-5，q=0，q=5时的广义Hurst指数hqmax、hq0、hqmin。

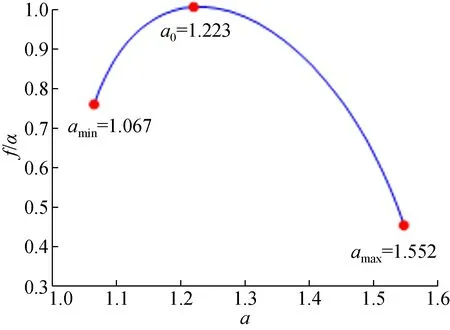
图4 sag信号的多重分形谱Fig.4 Multifractal spectrum of sag signal

图5 sag信号的广义Hurst指数Fig.5 Generalized Hurst index of sag signal

选取广义Hurst指数的最大值hqmax，多重分形谱的奇异指数的最小值αmin，多重分形谱最高点处对应的奇异指数α0；另外考虑到电能质量信号发生扰动时，其幅值大小会发生改变，信号所包含的能量值也会受到影响，因此可以用信号的能量值E作为其中一个特征量。其计算公式如下。

(11)

4 基于改进决策树的分类识别方法

C4.5以信息增益率作为属性选择判断条件，同时增加了同步剪枝的操作，增强了决策树模型的有效性。但计算信息增益率过程中大部分为对数运算，为提高运算效率，本文使用麦克劳林公式改进的决策树作为分类器。

4.1 C4.5决策树算法

对于一个随机变量S=[S1，S2，…，Si]，其中i=1,2,…,m，假设X是有m个不同属性的样本集，容量为n，每一类为Ci(i=1，2，…，m)，设Xi是每一类中的一个样本，定义样本分类所需的信息熵(也称期望信息)为：

(12)

对样本集X按照属性A划分为v个不同的类型，划分后的新的信息熵为：

(13)

原信息熵与划分后得到的新信息熵，二者间的差即为信息增益，

Gain(A)=Info(X)-InfoA(X)

(14)

信息增益进行规范化操作所需的参考分裂信息定义为：

(15)

信息增益率的计算方式为：

(16)

4.2 麦克劳林公式改进的C4.5决策树算法

从C4.5算法原理中不难发现，求取信息增益率的运算包含大量的对数计算，为减少计算时间，使用麦克劳林公式改进信息增益率的计算方式，转化成非对数的运算。式(12)中的信息熵转化为：

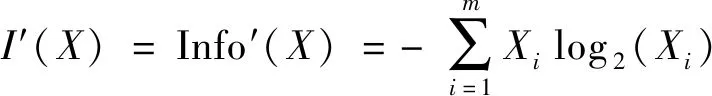
(17)

将ln(ni/n)用麦克劳林公式展开，得到：

(18)

式(17)由此可以简化为：

(19)

此时，式(13)中的新信息熵和式(15)中的分裂信息的计算式更新为：

(20)

(21)

改进后的信息增益率为：

(22)

式中：Gain′(A)=I′(X)-E′(A)，根据计算出信息增益率，生成决策树模型，利用if-then规则实现数据的有序划分。

5 实验及性能分析

本文采用的数据包括电压暂降、电压暂升、暂态振荡、谐波、闪变、脉冲等6种电能质量扰动信号。每种类型均通过MATLAB仿真实现，每种信号随机仿真100组，采样频率 5 000 Hz，信号长度为8 000点。

5.1 抗噪性能分析

将MFDFA方法分析得到的电能质量扰动信号的特征向量矩阵，作为输入数据由决策树分类器进行扰动识别，在随机仿真的100组电能质量扰动信号中，选取前70组作为训练样本，后30组作为测试样本。记电压暂降为标签1，电压暂升为标签2，暂态振荡为标签3，谐波为标签4，闪变为标签5，脉冲为标签6。

为了说明MFDFA方法的抗噪性能，用麦克劳林公式改进的C4.5决策树算法分别对测试集信号无噪声的条件下和加入噪声条件下的信号进行分类实验，得到图6和图7。图6是对无噪声信号进行分类的结果，图7是对加入不同程度高斯白噪声的信号进行分类的结果。

图6 无噪声测试集信号的MFDFA分类结果Fig.6 Classification results of the MFDFA to the test set signals without noise

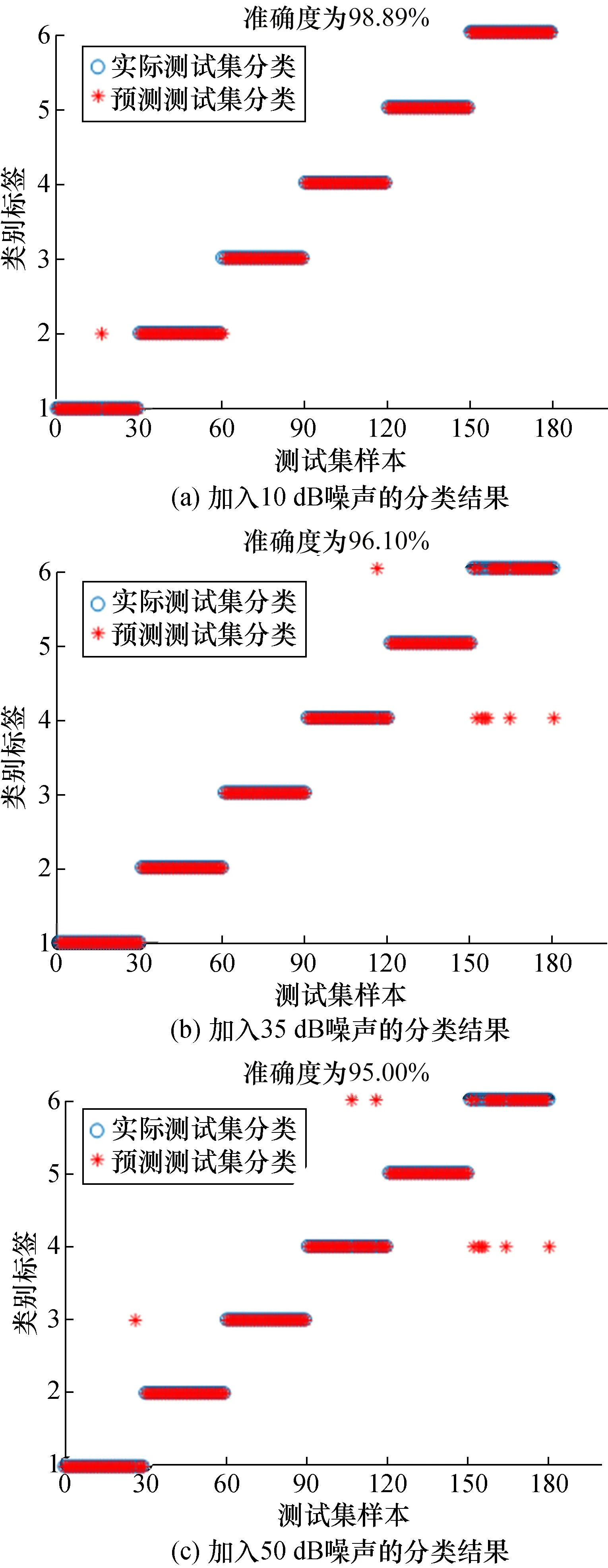
图7 加入噪声的测试集信号的MFDFA分类结果Fig.7 Classification results of the MFDFA to the test set signals added with noises

通过图6和图7的效果表明，利用MFDFA方法对无噪声测试集信号分类准确度达到100%、对加入噪声后的测试集信号分类准确度仍然较高(加入10 dB噪声的分类准确度为98.89%，加入35 dB噪声的分类准确度为96.10%，加入50 dB噪声的分类准确度为95.00%)。因此，MFDFA方法对无噪声和加噪声这两种情形分类准确性都比较高，证明了本文方法受噪声影响小，具有较好的抗噪性。

5.2 特征提取实验对比分析

使用DTCWT，HHT，EEMD三种常见的时频分析方法对上述电能扰动信号进行特征提取。以谐波信号(har)为例说明，图8是谐波信号的五层复小波分解结果图，图9是对谐波信号HHT变换后得到的高中低频分量，图10是经过EEMD变换后的各层IMF分量。

图8 谐波信号DTCWT分析Fig.8 Harmonic signal DTCWT analysis

图9 谐波信号的HHT分析Fig.9 Harmonic signal HHT analysis

图10 谐波信号的EEMD分解图Fig.10 Harmonic signal EEMD analysis

采用决策树对上述3种方法的分解结果进行分类，其中，决策树参数设置均与上文一致。表1为4种方法的分类准确度，可以看出由MFDFA方法提取出的特征量其分类精度高于其他3种方法。

从表2和图11中可以看出，4种特征提取方法中，MFDFA方法的识别准确率是最高的，其它3种方法由高到低依次是DTCWT、HHT和EEMD。

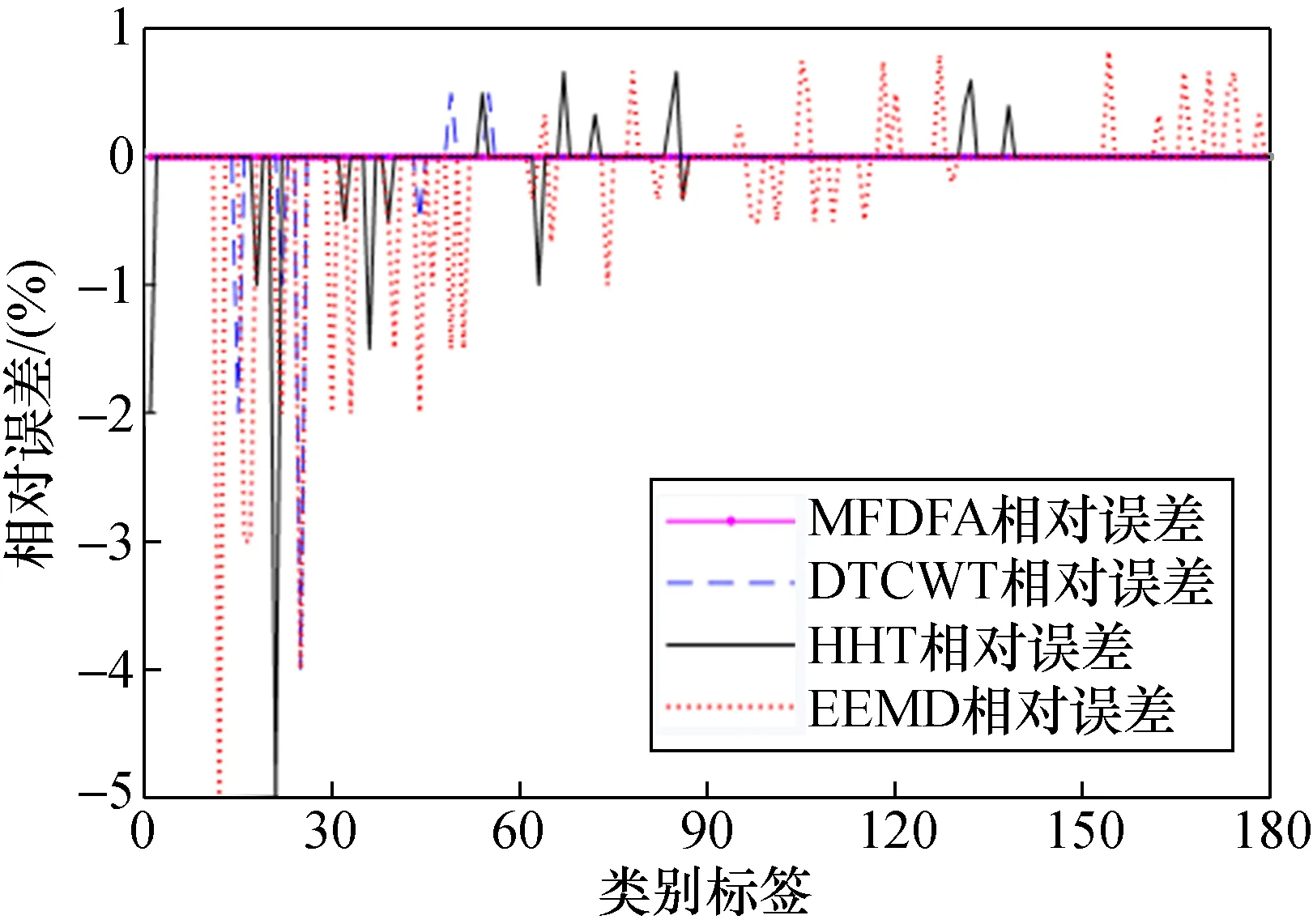
图11 不同方法的误差曲线Fig.11 Error curve for different methods

表2 不同算法的分类结果Tab.2 Classification results of different methods

表3给出了4种方法在信噪比为0、10、35、50 dB时的分类准确度，可以看出MFDFA方法提取的特征量识别率、抗噪性均优于其他3种方法。

表3 不同信噪比下的分类准确度Tab.3 Classification accuracy under different SND

6 结 论

本文首先证明了电能质量信号具有多重分形特征。据此提出利用多重分形去趋势波动分析方法提取3个分形参数，与信号能量共同作为特征向量，使用改进决策树作为分类器识别了6种常见的电能质量扰动信号。通过仿真实验验证，该方法在无噪声的情况下可以精确识别6种扰动信号，在有噪声的情况下该方法的分类准确度可达95%,表明了该方法具有较好的抗噪性能。通过与DTCWT、HHT和EEMD三种方法进行对比实验，结果表明本文所提方法表现出更好的识别结果，是一种电能质量扰动分析有效的新方法。