统计软件R 在数理统计教学中的探索与应用
王丽丽 赵 娟
(合肥学院<人工智能与大数据学院数学与统计系,安徽 合肥 230601)
0 引言
数理统计是理工科院校数学与统计专业的必修专业课,是一门从随机数据中获取信息、发现规律并指导决策的科学。 数理统计以概率论为基础,研究大量随机现象的统计规律, 其主要内容有参数估计、假设检验、方差分析和回归分析。由于计算机的应用,数理统计在自然科学、工程技术、管理科学及人文社会科学中的应用越来越广泛和深入,而传统的“理论+推导+例题讲解” 的上课方式已经无法满足数理统计的教学要求。 随着大数据时代的到来,计算机技术的普及和各种统计软件的广泛应用,减少数理统计教学中复杂理论知识的讲解和繁复的证明,着重介绍模型的应用背景和应用实例, 并介绍一款统计软件工具,力争每个实例都能以算法实现,就显得尤为重要了。
统计软件R 是以一种S 语言的扩展实现作图和数据分析的系统,是一个优秀的统计计算和可视化的软件。 相对于目前广泛使用的商业统计SAS、SPSS 软件而言,统计软件R 最大的特点是:开源,版本更新快,有大量的用于各种任务的库。 尤其是有许多使用统计软件R 的各领域的学者源源不断地提供最新和最前沿的开源软件包可供使用。本文着重介绍统计软件R 在数理统计教学中的探索与应用。
1 统计软件R
1.1 R 软件的下载及安装
用户可根据自己计算机所用的操作系统, 从R 官方网站或其遍及各国的CRAN 镜像站点选择对应的版本下载。目前R 最新版文件命名形式已统一为R-x.x.xwin.exe,直接运行,并选择安装目录及选装内容即可。
R 是一种解释型语言,输入的指令可以直接被执行。在提示符后可以以交互式的行命令方式一个个地输入指令,也可以创建一个脚本文件并以此方式运行所写的脚本文件。许多扩展的、新的开发包可以在“程序包”选单选择安装加载。
1.2 与统计计算有关的常用函数
常用函数:max(),min(),which.max(),which.min(),length(),sum(),prod(),mean(),median(),var(),cov(),cor(),std(),quantile(),summary(),rev(),sort(),order(),rank()常与统计函数联用的两个重要的函数:apply(),sweep()
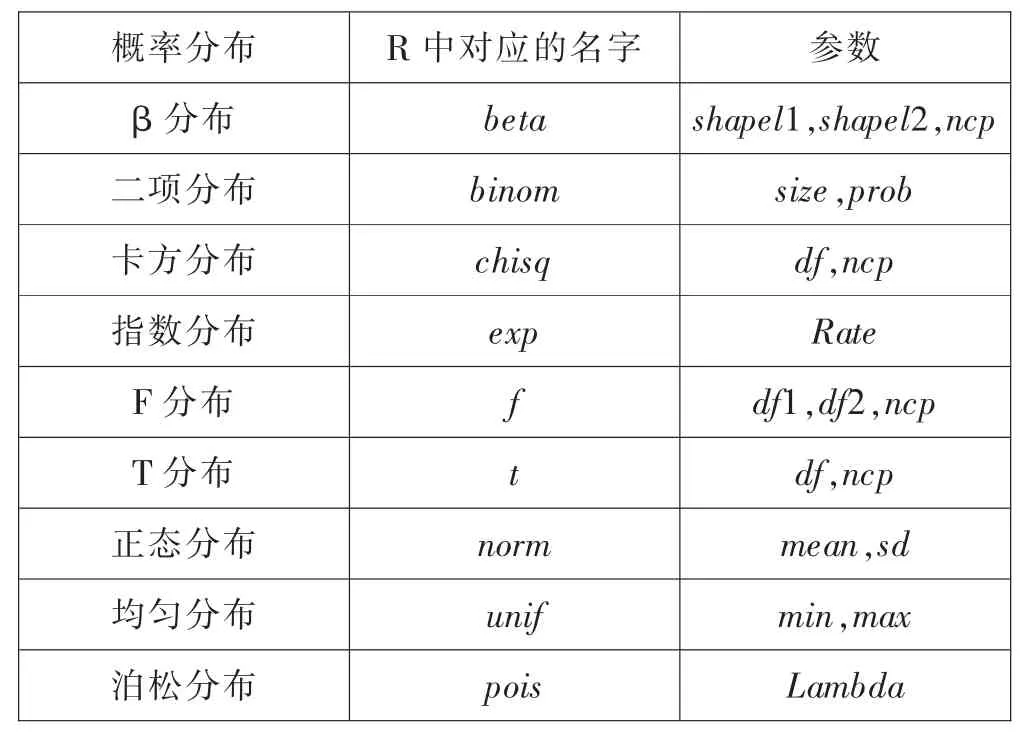
表1 R 中常用的分布函数
R 软件在统计分析时为处理方便准确,提供了更为细致的有关概率函数。 这些函数包括四类:d(密度函数),p(分布函数),q(分位数函数),r(随机数生成函数)。
2 R 在数理统计教学中的探索与应用举例
2.1 抽样分布中的应用实例及R 语言实现
数理统计第一章主要介绍基本概念理论,包括常见统计量如样本均值、方差、样本矩的计算;散点图、饼图、直方图、盒装图、茎叶图等的绘制;抽样分布、经验分布函数等的直观展示。 R 具有便捷的数据可视化系统,除了常规的图形之外,还可作出美观、个性化的图案,如小提琴图,脸谱图等。 在上课过程中,结合学生参加全国大学生市场调查与分析大赛的题目和调查问卷收集的数据,作出脸谱图,引起了学生极大的兴趣。 附R-语言程序及执行结果如下:


图1 脸谱图
在脸谱图中,脸的长度、宽度、脸型及嘴的高度、宽度分别代表着品牌的高端、性价比高、安全可靠、智能及方便。
2.2 参数估计中的应用实例及R 语言实现
数理统计第二章主要介绍的是参数估计,包括点估计中的矩估计和极大似然估计、区间估计、估计量的评价标准和克拉默-拉奥不等式。
例:已知某人分别搭乘公共汽车和地铁上班所需的时间数据,假设其服从正态分布。假设分别有65 分钟和58 分钟可用,问应选取哪种交通工具上班?
解:输入数据,R-语言程序及计算结果如下:

时间限制 65 时 P(x<=65)的估计:乘公汽 0.7233102;乘地铁0.7699699
时间限制 58 时 P(x<=58)的估计:乘公汽 0.5295298;乘地铁0.1969957
所以,假设有65 分钟可用,应乘地铁上班;假设有58 分钟可用,应乘公交车上班。
2.3 假设检验中的应用实例及R 语言实现
数理统计第三章主要介绍的是假设检验。假设检验是统计推断的一个重要方面,包括参数假设检验和非参数假设检验。
例:厂家A、B、C 是生产某一产品的知名企业,在过去的一年里,它们的市场占有率分别是15%、35%、25%。 厂家A 为了提高市场占有率,对该产品进行了改进。 现进行抽样调查,对销售出的200 件调查的结果如表2 所示:

表2 厂商销售量数据
依据调查数据对该产品的市场占有率是否发生变化做出判断,以便为厂家A 下一步的决策提供依据(显著性水平0.05)
解: 设 p1,p2,p3分别为厂家 A、B、C 的市场占有率, 现进行非参数假设检验:H0∶p1=0.15,p2=0.35,p3=0.25 R-语言程序及计算结果如下:

所以,不拒绝H0,即现有数据不拒绝“市场占有率未变”这一论断。
2.4 回归分析中的应用实例及R 语言实现
数理统计第四章介绍的是两种非常重要的统计方法:方差分析和回归分析。
例:某企业逐年用于技术改造资金x(单位:万元)与产品销售利润的增加额y(单位:万元)资料如下:

表3 某企业技术改造投入与销售利润数据
若使利润增加额以95%的概率在100 万~150 万元之间,利用一元线性回归预测,技术改造资金应在何范围内?
解:①建立一元回归方程;②预测。R-语言程序及计算结果如下:


通过观察t 检验和F 检验的p 值,可判断自变量和整个模型都是显著的。 技术改造资金应在38.87万~42.89 万之间,才能使利润增加额以95%的概率在100 万~150 万之间。
3 结论
数理统计是一门应用性非常强的学科,在近几年的教学过程中, 我们突出了数理统计基本思想的介绍,适当略去了复杂的公式推导和定理证明。 着重介绍统计方法和模型的应用背景和应用实例,并引入统计软件R,力争每个实例都能以算法实现,以期全面改善教学效果。
通过两个学期的教学实践,我们发现使用R 软件后, 学生摆脱了烦琐的计算,R 强大的互动性极大地激发了学生的学习兴趣。 未来,我们将进一步探索R在教学中的应用,使学生能够在领会各种统计方法的基本思想的基础上,自觉地、得心应手地借助R 软件来解决遇到的各种实际问题。

