一种基于差分进化的正弦余弦算法

刘小娟，王联国

甘肃农业大学信息科学技术学院，兰州 730070

正弦余弦算法（Sine cosine algorithm，简称SCA）是2016年由澳大利亚学者Seyedali Mirjalili提出的一种新型仿自然优化算法[1].该算法通过创建多个随机候选解，利用正余弦数学模型来求解优化问题，具有结构简单、参数少、易于实现的特点，但也存在优化精度低、容易陷入局部极值、收敛速度慢等问题.

近年以来，许多学者与研究人员对SCA进行了相关的研究与改进.其中，文献[2]通过分析转换参数，设计出转换参数抛物线函数递减和指数函数递减两种正弦余弦算法，并以协同过滤推荐算法中相似度函数的计算为应用对象，验证了改进指数函数递减正弦余弦算法的可行性和有效性；文献[3]通过引入惯性权重和反向学习策略，在提高算法收敛精度的同时加快了其收敛速度；文献[4]结合正弦余弦参数和候选解惯性权重提出了一种改进的正弦余弦算法，通过仿真实验说明了改进算法的有效性；文献[5]提出了一种基于改进正弦余弦算法的光谱特征峰识别定位方法，实验表明该方法在识别率等多方面均有显著提高；文献[6]提出了一种基于精英混沌搜索策略的交替正余弦算法，并将基于该策略的改进算法与反向学习算法交替执行以增强其探索能力，降低了算法时间复杂度并提高了收敛速度；文献[7]通过引入精英反向学习策略，并利用个体的反思学习能力对正弦余弦算法进行改进，提高了算法的寻优精度；文献[8]提出了一种基于非线性转换参数和随机差分变异策略的正弦余弦算法，并利用该算法优化神经网络参数以解决经典分类问题；文献[9]通过混沌策略和反向学习策略提出了一种基于改进正余弦算法的多阈值图像分割方法，对比实验结果表明该算法运行时间较短，分割精度较高，鲁棒性较强；文献[10]提出了一种以交叉策略改进的全局优化正弦余弦算法，并应用于图像分割中的多阈值分割；文献[11]提出了一种基于反向学习的自适应混合正弦余弦算法，并验证了该算法求解实际全局优化问题的有效性；文献[12]提出了一种新颖的混合BPSOSCA特征选择方法并进行聚类分析，与其它竞争方法相比该方法具有更优的性能；文献[13]提出了一种基于Riesz分数阶导数变异策略的正余弦算法，通过拟反向学习策略、反向学习策略和Riesz分数阶变异策略增强种群的全局探索能力并提高算法的收敛速度；文献[14]提出了一种用于文本分类的改进正弦余弦算法，避免了算法的早熟收敛；文献[15]提出了一种融合最优邻域和二次插值策略的改进正弦余弦算法，协调了算法的全局探索与局部开发能力；文献[16]提出了一种改进的正余弦算法，利用正交学习、多种群机制和贪婪选择机制，提高了算法的优化性能；文献[17]提出了一种用于全局优化和约束实际工程问题的多策略正余弦优化算法，将Cauchy突变算子、混沌局部搜索机制、基于反向学习策略等多种机制与基于差分进化的两种算子（变异和交叉）相结合，有效避免了算法陷入局部最优；文献[18]提出了一种基于带Lévy飞行的正余弦频带选择方法，实验结果表明所提出的频带选择方法在频带子集的选择上优于其它先进的分类方法，具有较高的分类精度.

为了更好地平衡算法的探索和开发能力，并使SCA既能从局部极值的邻域跳转到全局最优解的邻域，又能在全局最优解的邻域内进行高精度搜索，本文借鉴文献[19-21]中智能优化算法的混合方法，将差分进化算法与正弦余弦算法进行混合，提出了一种基于差分进化的正弦余弦（Sine cosine algorithm based on differential evolution，SCADE）算法.算法主要做了以下5方面的改进：（1）按非线性方式调整参数r1，并使每个个体采用相同的参数r1、r2、r3和r4，提高算法的搜索能力和收敛速度；（2）通过差分进化策略(包括交叉、变异、选择），充分利用全局最优个体的引导作用和种群中其它个体的信息，平衡算法的全局探索能力和局部开发能力；（3）利用侦察蜂策略，对个体适应度值连续nlim次没有进步的个体随机初始化，以增加种群多样性，提高全局探索能力；（4）利用全局最优个体变异策略，在最优解附近进行精细搜索，增强算法的开发能力，提高优化精度；（5）按固定迭代间隔，交替执行差分进化策略和全局最优个体变异策略.最后，对23个测试函数进行仿真实验，将SCADE算法与其它改进算法进行比较，验证SCADE算法的有效性.

1 正弦余弦算法

1.1 正弦余弦算法原理

SCA利用正弦函数和余弦函数的数学性质，通过自适应改变正弦函数和余弦函数的振幅来平衡算法在搜索过程中的全局探索和局部开发能力，并最终找到全局最优解.

设Xi=(xi1,xi2,···,xiN)为第i(i=1, 2,···,M) 个个体，N表示搜索空间的维度，M为种群规模，Pg=(pg1,pg2,···,pgN)为全局最优个体.在搜索过程中，第i个个体的第j维按式（1）进行位置更新.

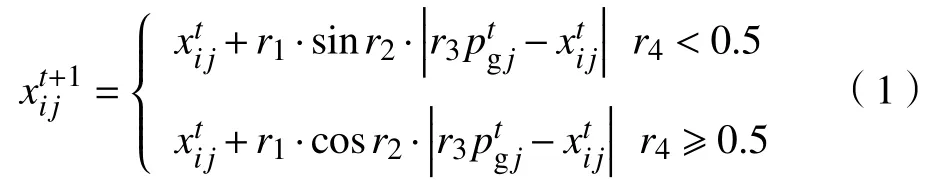
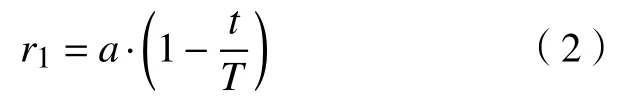
式中，T为最大迭代次数，a为常数，一般取值为2.

1.2 正弦余弦算法分析

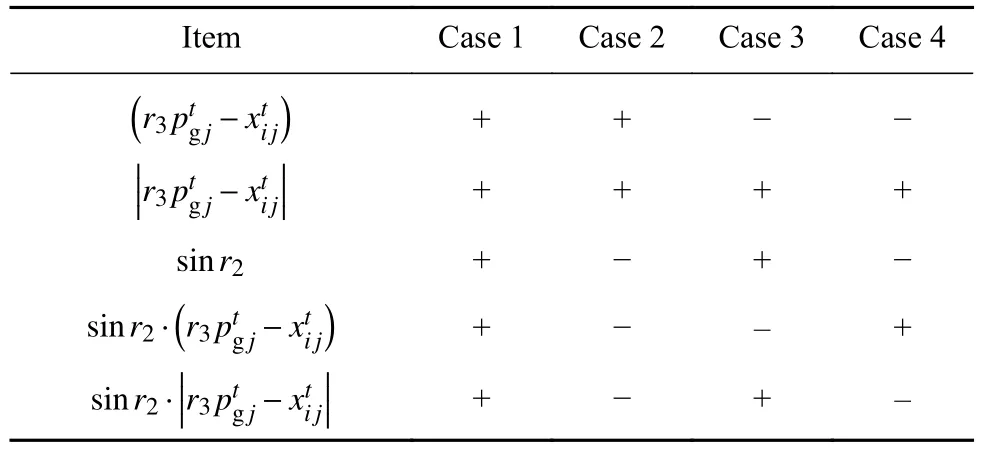
表1 sinr2的符号对2种分项符号的影响Table 1 Effect of the sign of sin r2 on the signs of two itemized items

（2）算法的收敛速度较慢.SCA按式（1）更新个体后，个体直接进入下一代，因此可以保持种群多样性，有利于全局探索，但算法收敛速度较慢，因此可以采用贪婪选择策略，使较优个体进入下一代，提高算法的收敛速度.然而，这却增加了算法陷入局部最优的可能性，故可采用侦察蜂算子，对较差个体进行随机初始化.

（3）第i个个体按式（1）更新时，只利用了全局最优个体Pg和第i个个体自身的信息，使第i个个体快速向全局最优个体Pg靠拢，容易造成算法陷入局部最优.

2 基于差分进化的正弦余弦算法

2.1 参数调整策略

2.1.1 按非线性方式调整参数r1

按非线性方式调整参数r1，调整策略见式（3）.通过改变参数r1的线性递减方式，使算法在迭代前期，SCA全局探索能力最强；在迭代中期，算法逐步从全局探索向局部开发阶段过渡；到迭代后期，r1非线性递减加快，使算法局部开发能力增强.

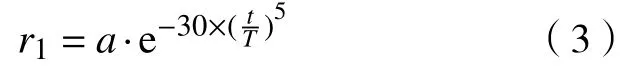
2.1.2 每个个体采用相同的参数r1、r2、r3和r4

在每次迭代中，每个个体的所有维度采用相同的参数r1、r2、r3和r4，使每个个体所有维度以相同方式与比例进行搜索，降低算法的随机性，提高算法的搜索能力和收敛速度.

2.2 差分进化策略

2.2.1 差分变异操作

差分变异利用父代种群中的多个个体的线下组合生成变异个体Vi=(vi1,vi2,vi3,···,viN)，在改进算法中利用式（4）生成变异个体Vi.

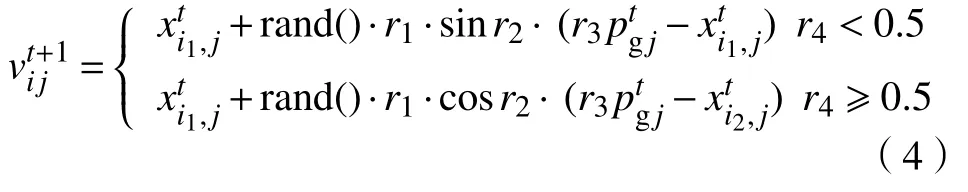
式中，rand()为[0, 1]上的随机数，i1和i2是在当前种群中随机选择的2个个体，并且i1≠i2≠i.该变异操作既利用了全局最优个体Pg，又利用了种群中其它个体的信息，较好地平衡了算法的全局探索能力和局部开发能力，防止算法陷入局部最优.

2.2.2 交叉操作

交叉操作通过变异个体Vi=(vi1,vi2,···,viN)和Xi的各维度分量的随机重组产生交叉个体Ui=(ui1,ui2,···,uiN)，提高种群多样性，Ui按式（5）产生.

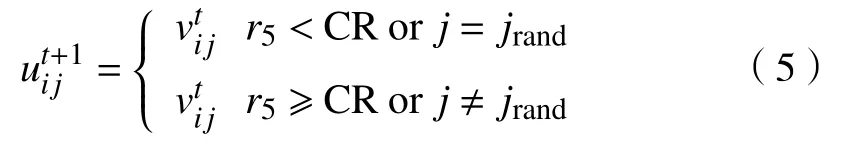
式中，CR为交叉概率常数，r5为[0, 1]上的随机数，jrand∈{1, 2,···,N}为随机选择的维度索引，它保证Ui至少要从Vi中获得一个元素，以确保有新的个体产生.

2.2.3 选择操作

采用贪婪选择策略，根据Xi和交叉个体Ui的适应度值f(·)来选择较优个体进入下一代.对于最小化问题，其选择操作按式（6）进行.

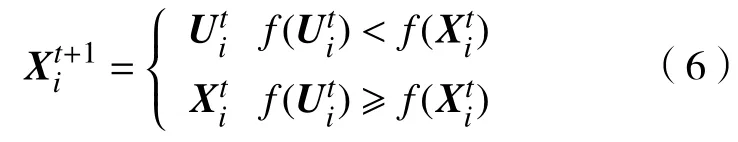
2.3 侦察蜂策略

采用了贪婪选择策略，加快了算法的收敛速度，但随着迭代的进行，算法收敛于全局最优解和局部最优解.为了防止算法陷入局部最优，采用人工蜂群（ABC）算法中的侦察蜂算子，对个体适应度值连续nlim次没有进步的个体随机初始化，以增加种群多样性，提高全局探索能力.

2.4 全局最优个体变异策略

以提高算法优化精度和收敛速度为目标，对全局最优个体Pg按式（7）和（8）进行高斯变异操作，生成新个体，如果的适应度值优于Pg，则用替代P.g

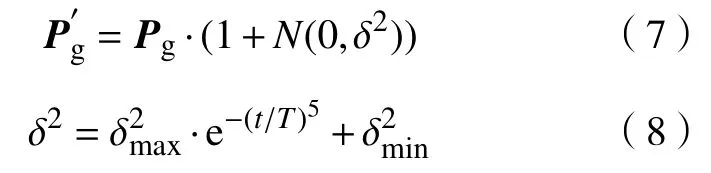
式中，δ2为方差，按式（8）产生，δ2max和δ2min分别为方差变化的最大值和最小值.这种处理使算法在迭代搜索前期注重全局探索，而在迭代搜索后期主要进行局部开发，这在一定程度上提高了算法的优化精度.

为了减少算法时间复杂度，每隔h次迭代，执行kmax次小规模的全局最优个体变异策略.一般情况下，满足kmax≤M.

2.5 算法步骤及流程

SCADE算法的步骤如下：

步骤1：随机产生种群M个个体，设置当前迭代次数t，最大迭代次数T，交叉概率常数CR，方差变化的最大值δ2max和最小值δ2min，执行全局最优个体变异策略的迭代间隔h和迭代次数kmax；

步骤2：计算每个个体的适应度，并找出全局最优个体Pg；

步骤 3：计算r1；

步骤 4：当tmodh==0时，按式（7）和（8）执行kmax次小规模的全局最优个体变异策略，转向步骤8，否则转向步骤5；

步骤 5：按式（4）～（6）更新每个个体；

步骤6：更新全局最优个体Pg；

步骤7：执行侦察蜂策略；

步骤8：终止条件是否满足？若满足，停止迭代并输出全局最优解，否则转向步骤3.

SCADE算法对应的流程图如图1所示.

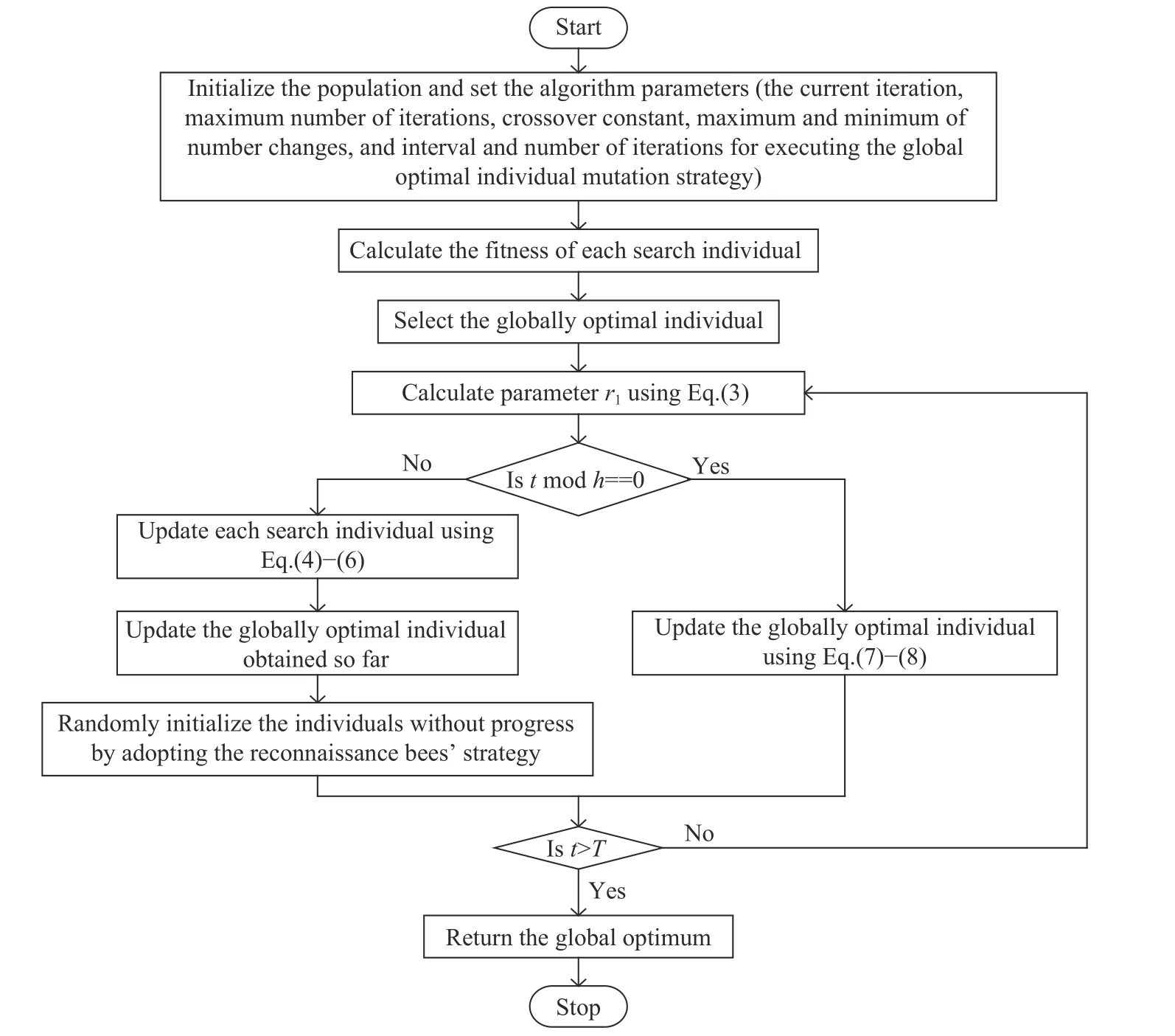
图1 SCADE算法流程图Fig.1 Flowchart of the proposed SCADE algorithm

2.6 算法时间复杂度分析

SCADE算法的时间复杂度主要由差分进化、侦察蜂策略和全局最优个体变异策略3部分组成.假设种群规模为M，问题维度为N，最大迭代次数为T，每隔h次迭代，交叉概率常数CR，执行kmax次小规模的全局最优个体变异策略，当种群中每个个体适应度值连续nlim次没有进步时，在解空间中随机产生一个新个体进行替换，则SCADE算法的时间复杂度为：

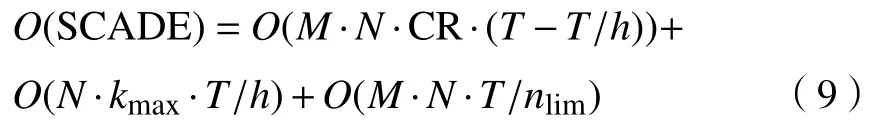
SCA的算法时间复杂度为：

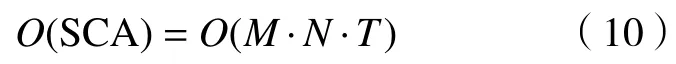
3 仿真实验

3.1 实验设计

实验环境配置为：操作系统Windows 8.1，处理器Intel_Core_i3-4150_CPU_@_3.50 GHz，内存4G，编程语言Microsoft Visual C++ 6.0.本文选取文献[1, 22]中的23个基准测试函数（函数表达式详见文献），以求函数最小值为例进行仿真实验以评价SCADE算法的优化性能.其中，F1～F7为单峰函数，F8～F13为多峰函数，F14～F23为固定维度多峰函数.各算法设置的具体参数见表2.其中，PSO中Vmax和W分别为微粒的飞行最大速度和惯性加权系数，DE中F为常量因子，m-SCA中JR为跃变率，COSCA中pr 为选择比例，astart和aend分别为控制参数a的初始值和最终值.最终测试结果采用独立运行30次后的平均值，实验结果如表3、表4和图2所示.

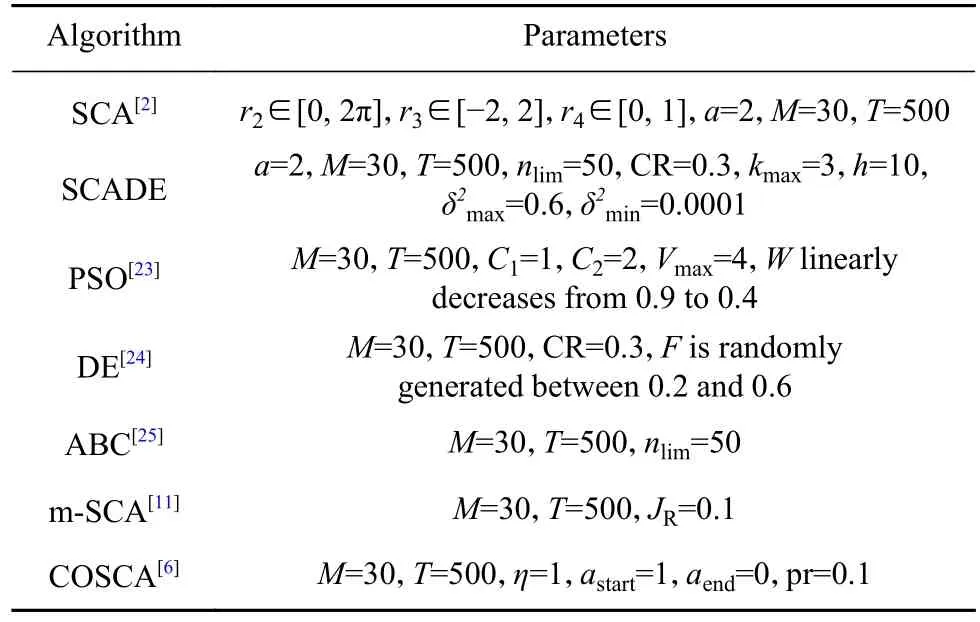
表2 各算法设置的具体参数表Table 2 Specific parameters set by each algorithm

3.2 评价标准

通过算法找到的平均最优值、中值、最优值、最差值、标准差、平均运行时间和收敛曲线图等7个方面评价算法的性能.其中平均最优值反映算法的优化精度，中值、最优值和最差值反映可行解的质量，标准差反映算法的稳定性，平均运行时间反映算法执行的时间代价，收敛曲线图反映算法的收敛情况.

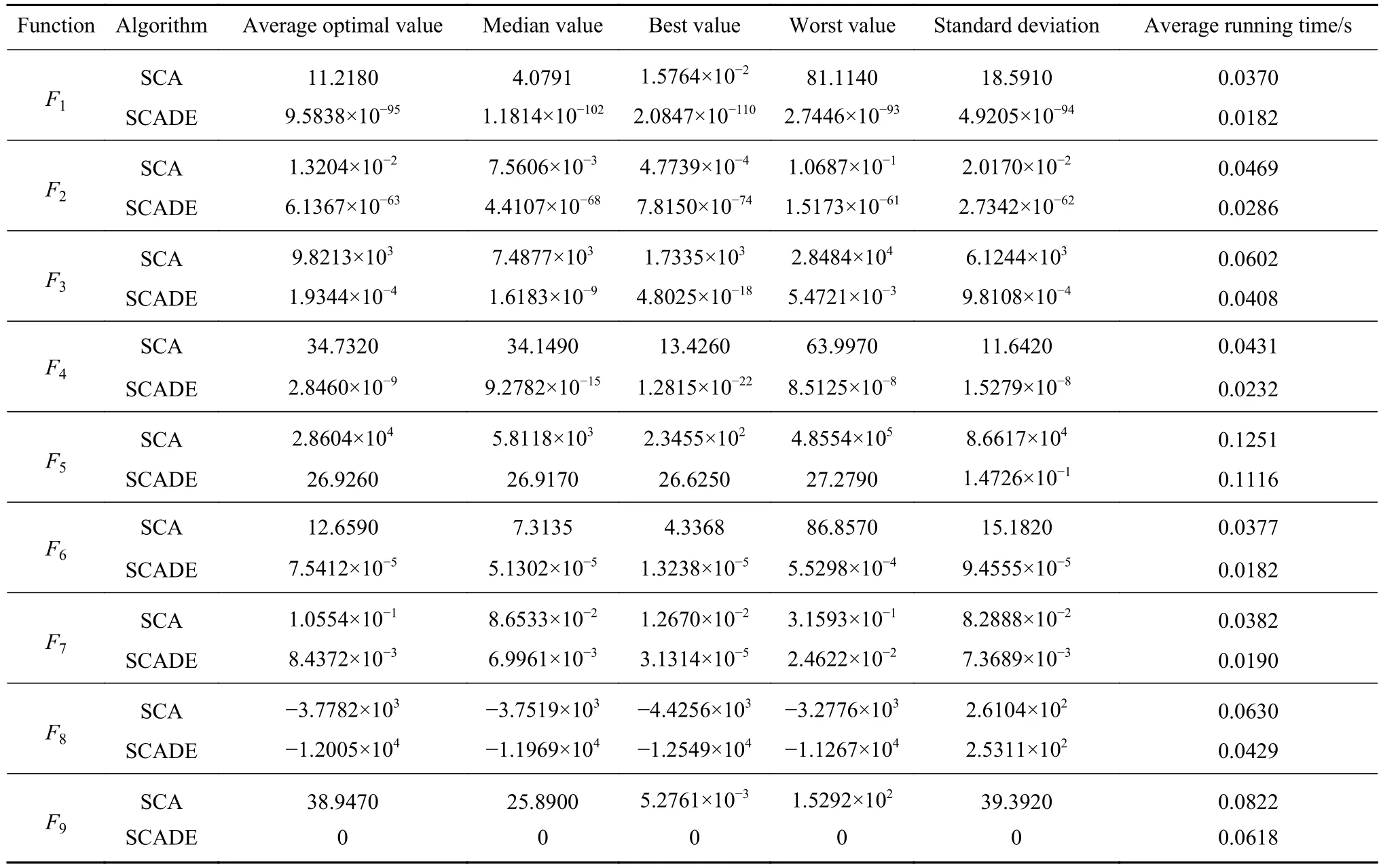
表3 SCADE与基本SCA的实验结果Table 3 Experimental results of SCADE and basic SCA

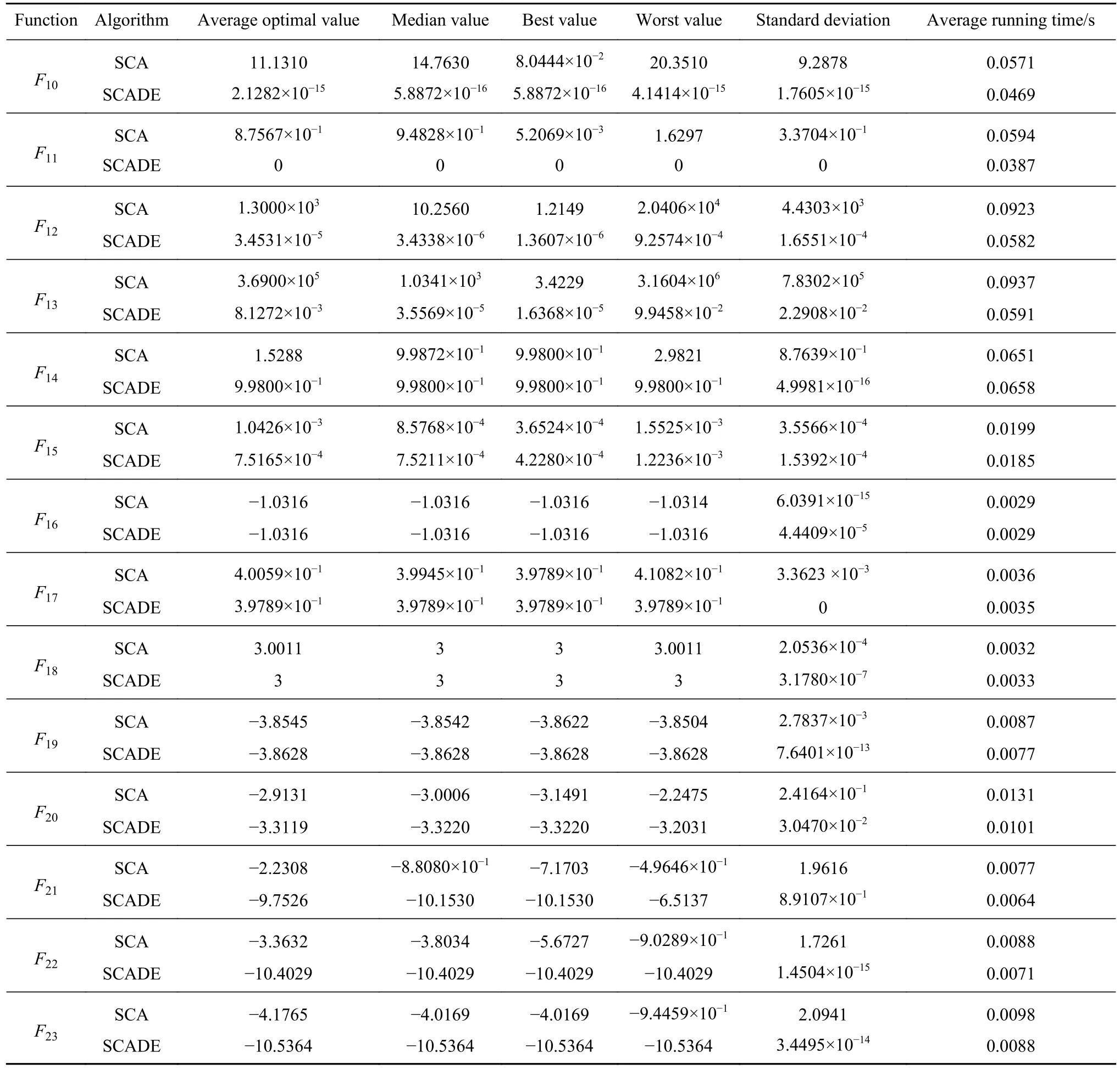
表3 (续)Table 3 (Continued)

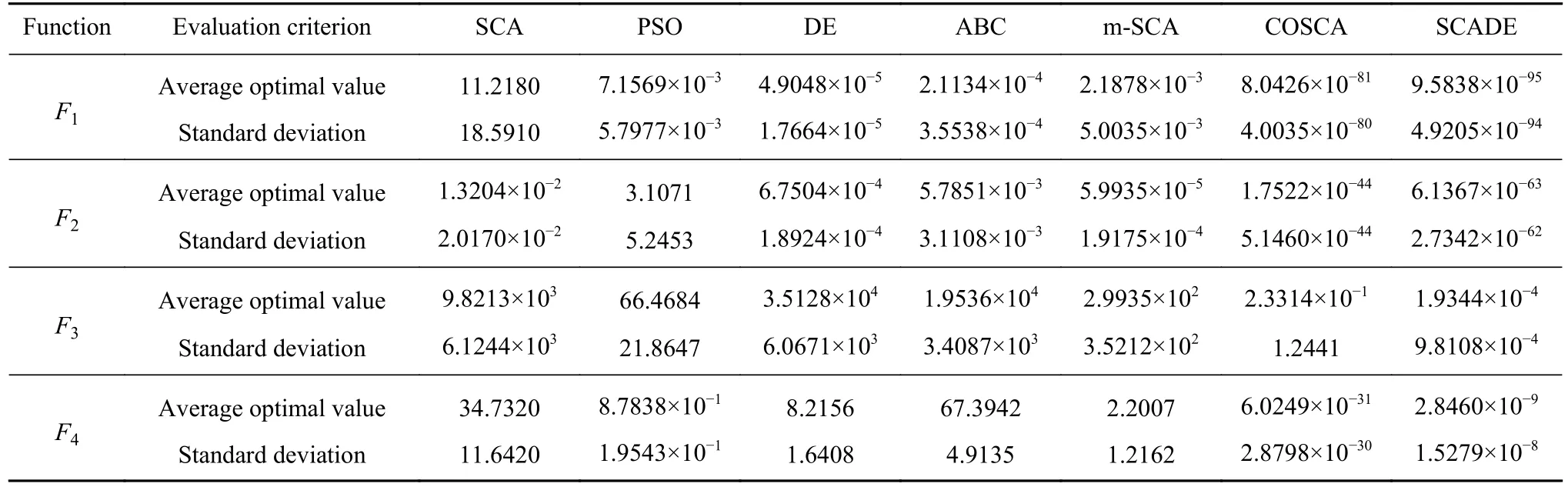
表4 SCADE与SCA改进算法及其它智能优化算法的性能比较Table 4 Performance comparison of SCADE with modified SCA and other algorithms

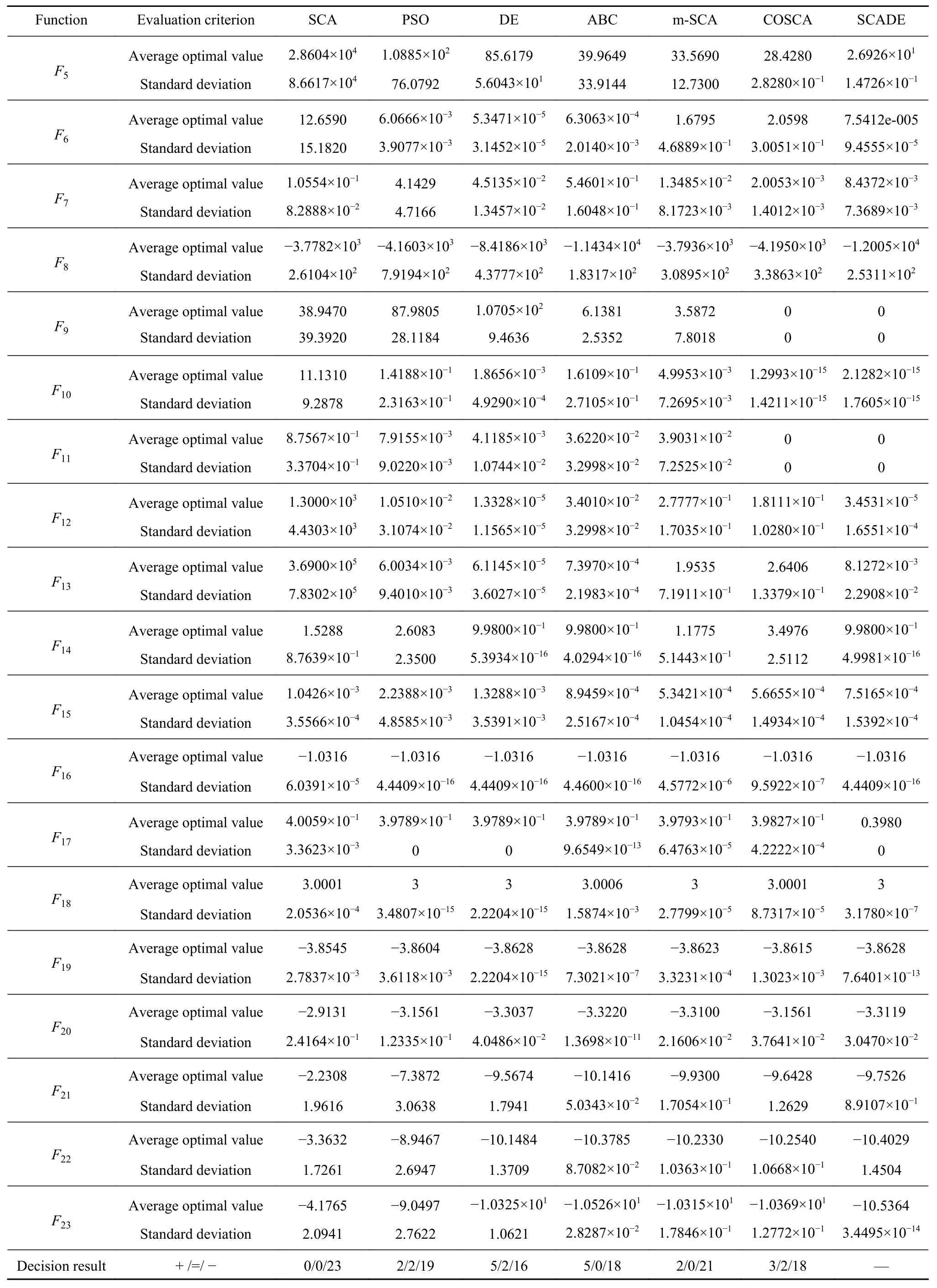
表4 (续)Table 4 (Continued)

3.3 SCADE 与基本 SCA的性能比较

为了测试改进算法SCADE相比基本SCA的寻优性能，2种算法参数设置见表2，并采用相同的函数最大评价次数15000.表3列出了改进算法SCADE与基本SCA的测试结果对比情况.

由表3可以看出：在算法获得的平均最优值和标准差方面，SCADE对函数F16、F18和F19的优化结果中的平均最优值与SCA相当，标准差优于SCA，但对其余的20个测试函数，所获得的优化结果明显优于SCA，而且优化精度较高；在算法获得的中值、最优值和最差值方面，SCADE对函数F15、F16、F17和F18的优化结果与SCA相当，在其余测试函数上所获得的优化结果仍明显优于SCA，表明SCADE获得的可行解质量较高；在算法获得的运行时间方面，相比SCA，SCADE除了函数F14、F16和F18稍长或相等外，在其余测试函数上运行时间最短，这是因为SCADE中去掉了绝对值运算符，采用了差分进化策略，只对部分维度进行更新，减少了计算量，从而缩短了算法的运行时间.

3.4 SCADE 与 SCA 改进算法及其它智能优化算法的性能比较

为进一步测试改进算法的性能，将SCADE与SCA改进算法及其它智能优化算法PSO、DE、ABC、m-SCA、COSCA进行比较.参数设置同上文，函数最大评价次数仍保持一致.另外，采用显著性水平为5%的Wilcoxon秩和检验以评价算法的寻优性能.

3.4.1 优化精度分析

表4列出了改进算法SCADE与上述算法在23个测试函数上的平均最优值、标准差及秩和检验决策结果（+ /=/-）.其中，决策结果“+ /=/ -”分别表示通过Wilcoxon秩和检验后对比算法“优于/相当/逊于”SCADE算法的函数个数.

由表4可以看出：SCADE在12个测试函数上获得的优化结果优于其它对比算法，且在多峰函数F9、F11、F14、F16、F17、F18、F19、F22和F23上均已取得理论最优值.同时，从秩和检验结果可知，SCADE在23个测试函数上的结果优于SCA，在19个测试函数上的结果优于PSO，在16个测试函数上的结果优于DE，在18个测试函数上的结果优于ABC，在21个测试函数上的结果优于m-SCA，在18个测试函数上的结果优于COSCA.

3.4.2 收敛性分析

图2是7种算法在部分测试函数中运行30次后得到平均最优值收敛曲线图.除了图2（c）和（f）外，其余函数收敛曲线图的纵坐标为函数平均最优值的对数值，横坐标为迭代次数.

从图中可以看出：在单峰测试函数中，对于F2，相比其它6种算法，SCADE收敛速度明显加快，同时优化精度最高，并且相比基本SCA达到了60次方数量级的优化效果.对于F5，SCADE与COSCA的收敛趋势一致，但SCADE收敛速度更快，得到的解较好；在多峰测试函数中，对寻优难度较大的F8而言，在迭代前期，SCADE收敛速度高于基本SCA、DE、PSO、m-SCA和COSCA，但在迭代中期，SCADE的收敛速度显著加快，并且在迭代次数约350次时开始收敛直到趋向全局最优解.对具有许多局部极小值的F10而言，在迭代次数小于150次时，SCADE和COSCA的收敛趋势基本一致，并且收敛速度大于其它6种对比算法，当迭代次数大于150次时，SCADE同COSCA以相等的收敛速度和优化精度不断收敛；在固定维度的多峰测试函数中，对于F14，相比其它5种算法，SCADE同ABC收敛趋势和优化精度基本一致，且好于DE、PSO以及SCA的改进算法m-SCA和COSCA.对于F23，相比其它6种算法，SCADE前期的收敛速度略低于ABC和DE，但当迭代次数达到400次左右时，SCADE能优于PSO、m-SCA和COSCA达到其理论最优值.

综上所述，相比基本SCA、SCA改进算法及其它智能优化算法，本文提出的算法SCADE收敛性较好，优化精度更高，稳定性和鲁棒性更强.

3.5 重要参数分析

3.5.1 连续次数nlim

在ABC算法的侦察峰策略中，连续次数nlim的选取对算法性能的影响显得尤为重要.一般而言，nlim的设置不能太小[26].因此，选取不同峰型、具有代表性的3个测试函数，通过仿真实验分析不同取值的nlim对SCADE性能的影响.仿真实验中，考虑到算法的最大迭代次数为500，故在范围[0, 100]内设置不同间隔的nlim值，其它参数设置见表2，同时用显著性水平为5%的Friedman检验反映实验结果的差异性.表5列出了不同nlim的值对SCADE性能影响的实验结果，影响指标包含平均最优值、标准差、排序及Friedman检验的概率值P.从表5可以看出，除测试函数F2外，其它函数的Friedman检验概率值P均小于0.05，这说明不同的nlim设置下实验结果存在一定的差异性.根据表中函数结果显示，当nlim等于50时算法性能最优，故本文设置参数nlim的值为50.

3.5.2 交叉概率常数CR

交叉概率常数CR在SCADE算法中起关键作用.通过仿真实验分析不同取值的交叉概率常数CR对SCADE性能的影响.在[0.1, 0.5]范围内以0.1的间距设置CR的值，测试函数及其它参数设置见表2，表6列出了不同取值的CR对SCADE的性能影响.由表6可见，除测试函数F2外，其余函数的Friedman检验概率值P均小于0.05，这说明在不同的CR设置下，实验结果仍存在差异性.同时，表中函数结果显示，当CR等于0.3时算法性能最好，故本文设置参数CR的值为0.3.

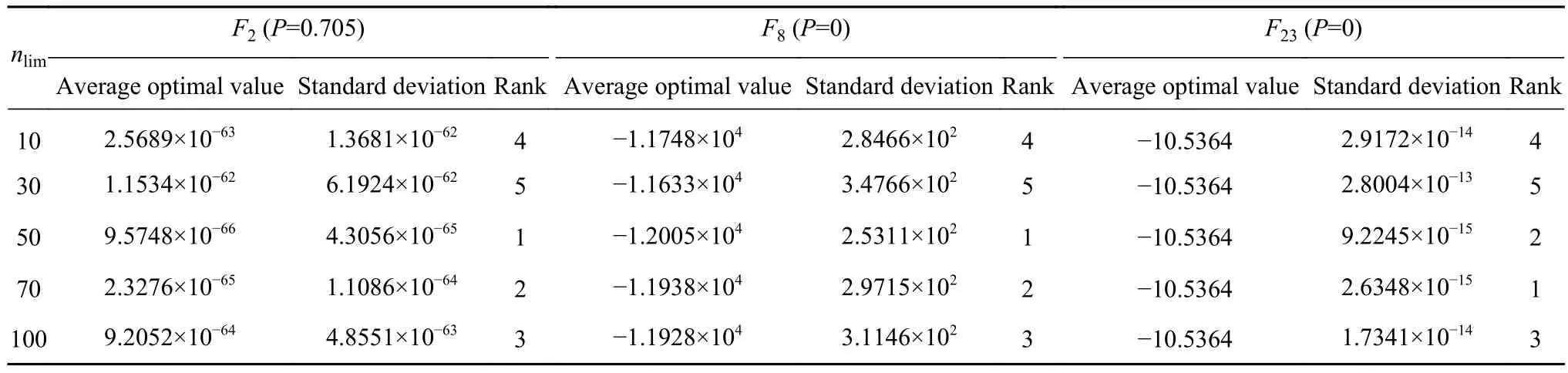
表5 nlim对SCADE的性能影响Table 5 Influence of nlim on the SCADE performance

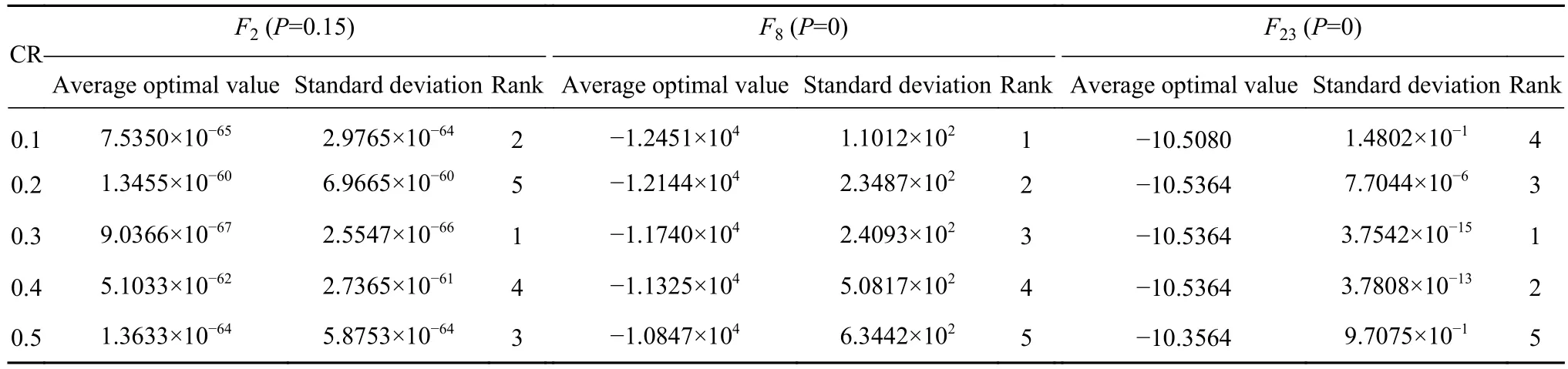
表6 CR对SCADE的性能影响Table 6 Influence of CR on the SCADE performance

3.5.3 迭代间隔h

为提高算法的优化精度，每隔h次迭代，执行小规模的全局最优个体变异策略.在[5, 25]范围内以5的间距设置h的值并进行实验，测试函数及其它参数设置同见表2.表7列出了不同取值的h对SCADE性能的影响.表中所有函数的Friedman检验概率值P均小于0.05，同样说明不同的h设置下实验结果存在差异性.另外，表中测试函数结果显示，h等于10时算法寻优效果较好.

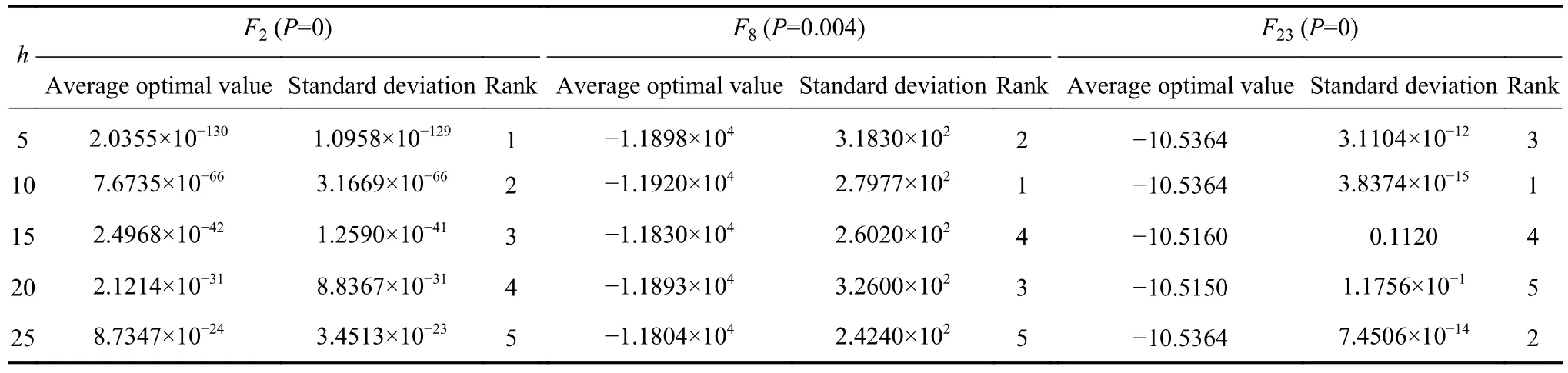
表7 h对SCADE的性能影响Table 7 Influence of h on the SCADE performance

4 结论

针对SCA在优化部分高维函数问题时的缺陷，提出了一种基于差分进化的正弦余弦（SCADE）算法.本文所做的主要工作总结为：（1）通过去掉SCA位置更新公式中的绝对值，降低算法的计算复杂度；（2）通过参数调整策略，提高算法的搜索能力和收敛速度；（3）通过交替执行差分进化策略和全局最优个体变异策略，较好地平衡算法的全局探索能力和局部搜索能力；（4）通过利用侦察蜂策略，增加种群多样性，并提高全局探索能力；（5）通过选取有代表性的不同峰型测试函数进行Friedman检验，反映出连续次数、交叉概率常数和迭代间隔的特定取值对SCADE算法性能影响较敏感；（6）通过23个测试函数的仿真实验，并与其它改进算法进行比较，结果表明SCADE算法具有较高的优化性能.最后，下一步的工作将是研究如何运用SCADE算法解决实际优化问题.