旋转曲面关于积分第一中值定理中ξ 的变化趋势
2021-01-04 08:31:50方绍威喻晓
上饶师范学院学报 2020年6期
方绍威,喻晓
(上饶师范学院 数学与计算机科学院,江西 上饶334001)
1 引言及主要结论
众所周知,积分中值定理在分析数学中扮演着重要角色,具体叙述如下:
定理A[1](积分第一中值定理):若函数f(x)在闭区间[a,b]上连续,则在积分区间[a,b]上至少存在一个点ξ,使下式成立:

定理B[1](推广的积分第一中值定理):如果函数f(x)、g(x)在闭区间[a,b]上可积,且g(x)在[a,b]上不变号,f(x)连续,则在积分区间上至少存在一个点ξ,使下式成立:关于中值定理渐近性的研究,在一元函数的情况下,文献[2]已经对其做了充分的讨论,其主要结论如下:
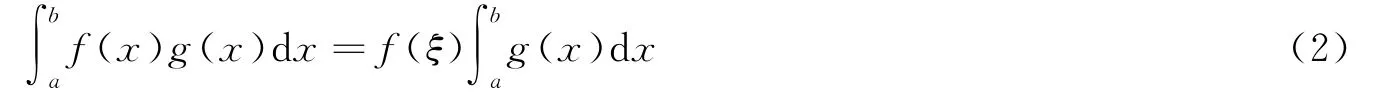
定理C[2]设η 是区间[a,b]中某点,存在实数a >0,β ≥0,A,B≠0,I,如果:

本文主要研究对象为xoz平面上的函数z(x)-f(x)g(x)绕z轴旋转一周后形成旋转曲面z(x,y)=
设上述旋转曲面在定义域x2+y2≤r2上的积分为V1,接下来对V1作近似估计。
对上式化简并使用定理B有:
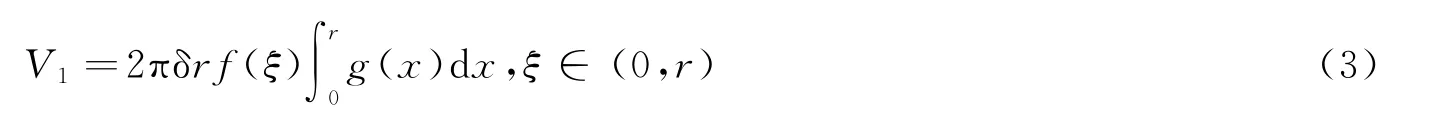
本文即是对(3)式中ξ点渐近规律的一个探讨。现主要结论如下:
定理1设函数f(x)、g(x)满足:

2 本文主要引理
引理1[3]曲线为平面光滑曲线,绕直线l:Ax+By+C=0一周所成旋转体的体积的积分公式为:
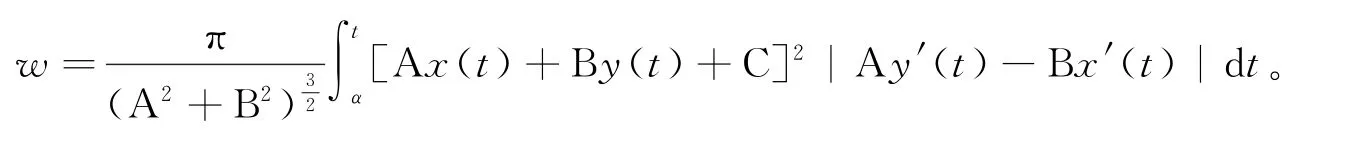
3 定理1的证明
设xoz平面上的函数z(x)=f(x)g(x)绕z轴旋转一周后的旋转体体积为V2,根据引理1得:
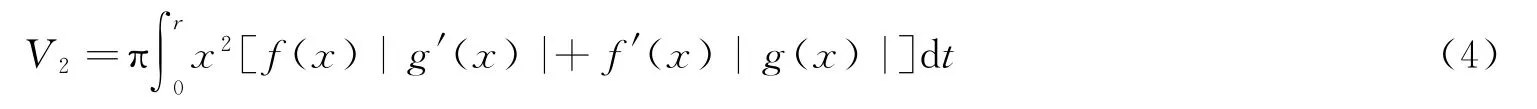
由于(3)式的V1计算的是旋转曲面对xoy平面所求积分的体积,以及(4)式的V2所计算的是旋转曲面上方旋转体的体积,于是有:V1+V2=πr2f(η)g(η)。
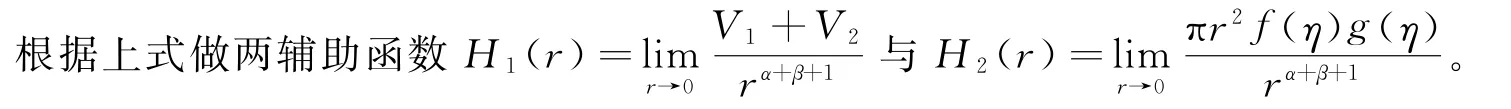
易得:

下面开始计算H1(r):

使用洛必达法则可化简为:
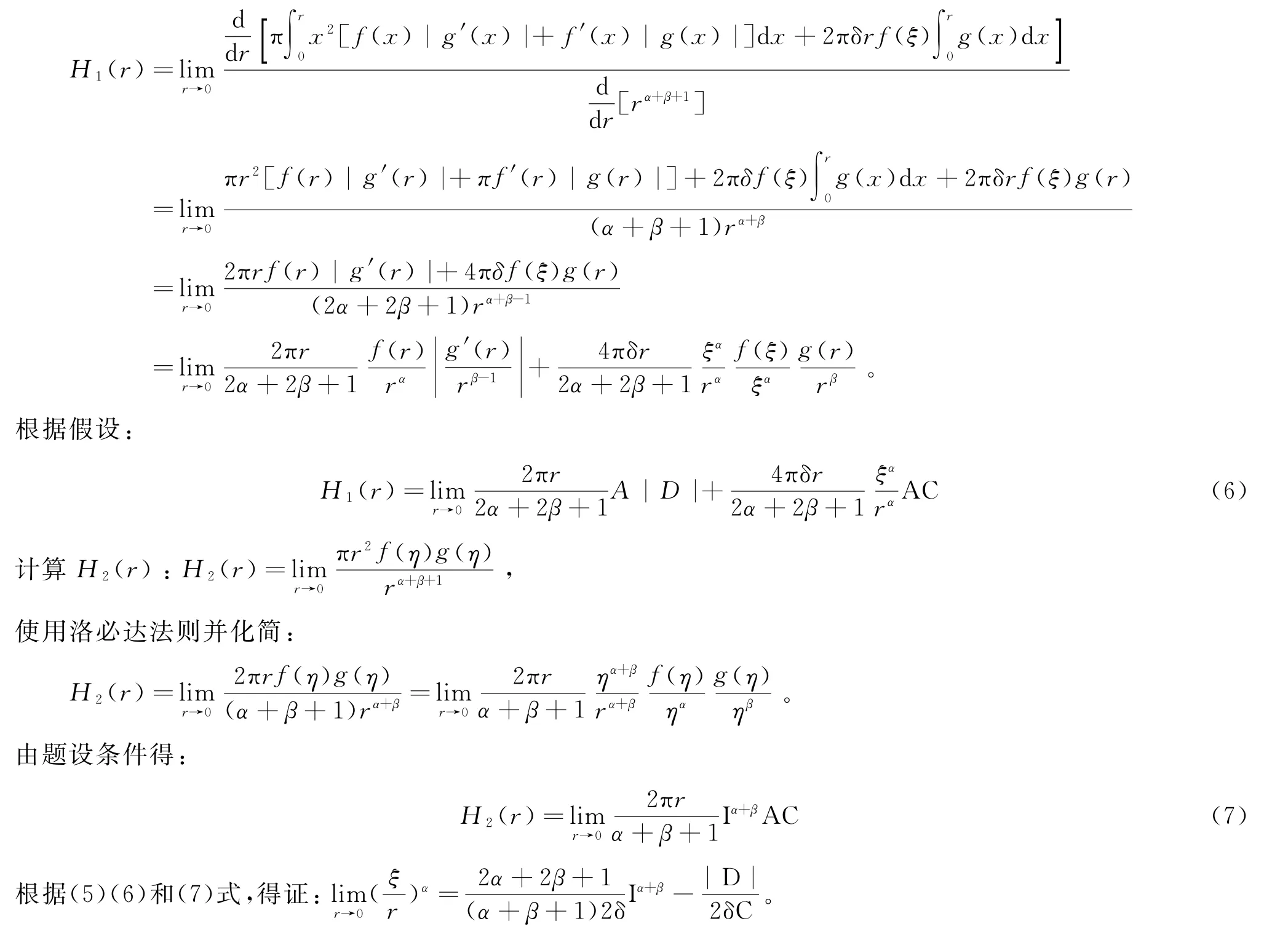
猜你喜欢
小学生学习指导(高年级)(2022年10期)2022-11-04 06:20:50
高师理科学刊(2020年12期)2020-03-15 09:55:44
数学年刊A辑(中文版)(2019年1期)2019-01-31 02:35:28
数学物理学报(2018年5期)2018-11-16 05:49:44
新教育时代·教师版(2018年18期)2018-07-21 11:00:06
中学生数理化·七年级数学人教版(2017年3期)2018-01-20 12:45:54
数学学习与研究(2016年23期)2017-03-15 16:31:23
中学生数理化·七年级数学人教版(2017年12期)2017-02-15 09:56:01
中学生数理化·七年级数学人教版(2017年12期)2017-02-15 09:56:01
考试周刊(2016年82期)2016-11-01 13:00:24

