2020年全国高考数学一卷(理)20题解法赏析

陈志年

(安徽省合肥市肥西中学 231200)

2020年全国高考数学一卷(理)20题是一道解析几何题，其中第二问是证明直线过定点.虽然是一类常见常考的题型，但是解决起来有一定的难度.难点在于：引进一个参数，思路简单，可运算量大，要求运算流畅、准确；引进多个参数，最后涉及到参数的消去与保留，要求思维灵活、缜密.下面给出该题的多种解法及评析，欣赏一题多解的妙趣；领略难点突破的秘诀.

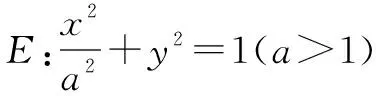
(1)求E的方程；(2)证明：直线CD过定点.

评析本解法两次将直线方程代入椭圆方程得到关于x的一元二次方程,有一定的运算量，要求零失误;利用韦达定理求得C、D的坐标，是一个技巧;写出直线CD的方程还需要化简整理，方能得到所要证的结论.

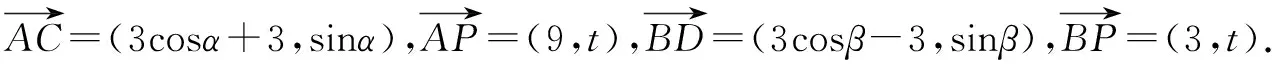
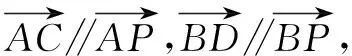
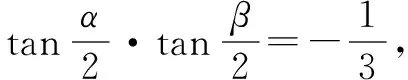
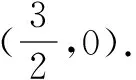
评析本解法利用椭圆的参数方程设点的坐标，减少了参数的个数；整个解答过程中，利用了多个三角公式，如：同角三角函数基本关系公式，两角和与差公式，二倍角公式及通过角的变换推导的“和差化积”公式等，可以说三角公式的运用得到了极致.

解法3由(1)知A(-3,0),B(3,0).设P(6,t)，根据对称性直线CD所过定点在x轴上.

消去m得 -(n2-9)(y1+y2)+3n(n-3)y1-n(n+3)y2=0，

当t=0时，直线CD的方程为y=0.

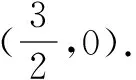
根据对称性直线CD所过定点在x轴上.

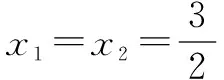
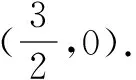
评析本解法引进更多的参数，利用C、D在椭圆上，我们首先消去y1和y2，得到4x1x2-15(x1+x2)+36=0，至此应用韦达定理解答显而易见，水到渠成.解析几何中，设而不求、加强韦达定理的应用是解答问题的重要方法.