山东省高考22题
——一个圆锥曲线性质的推广
2021-01-04 13:23苏凡文
数理化解题研究 2020年31期
苏凡文
(山东省泰安宁阳一中 271400)
(1)求C的方程;
(2)点M,N在C上,且AM⊥AN,AD⊥MN,D为垂足.证明:存在定点Q,使得|DQ|为定值.

(2)①直线MN不垂直于x轴时,设
MN:y=kx+m,M(x1,y1),N(x2,y2).
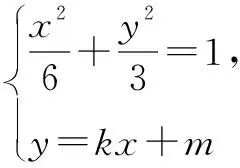
消去y可得(2k2+1)x2+4kmx+2m2-6=0.

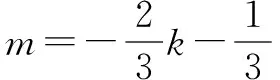
m=1-2k时,MN:y=k(x-2)+1,直线MN过定点A(2,1),舍.
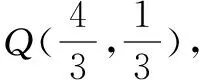

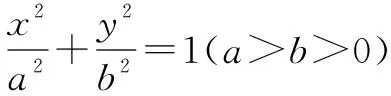

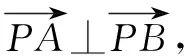
联立直线AB与椭圆方程得
(b2+k2a2)x2+2kma2x+(m2a2-a2b2)=0,
由韦达定理有


又A、B都在直线AB上,则有
y1=kx1+m,y2=kx2+m,
两式相加得

两式相乘得
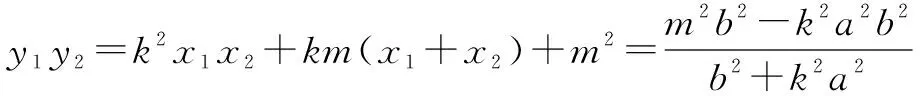
将②③④⑤代入①得

因P不在直线AB上,则kx0+m-y0≠0,所以有a2(kx0+m+y0)=b2(y0-m+kx0),
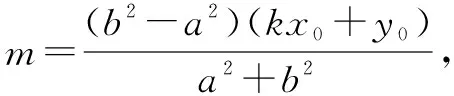

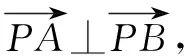


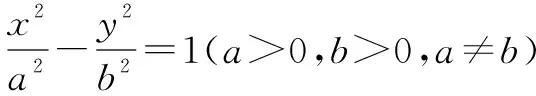

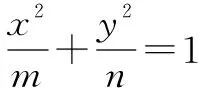
推广六点P(x0,y0)为抛物线y2=2px(p>0)上任意一点,过点P作PA⊥PB,PA、PB与抛物线分别交于异于点P的点A、B,则直线AB过定点(x0+2p,-y0).
猜你喜欢
中学生数理化(高中版.高二数学)(2022年1期)2022-04-26
新世纪智能(教师)(2021年2期)2021-11-05
数学小灵通·3-4年级(2021年5期)2021-07-16
中学数学杂志(高中版)(2021年2期)2021-06-02
中学数学杂志(高中版)(2021年3期)2021-05-10
河北理科教学研究(2020年4期)2020-03-09
电子制作(2018年10期)2018-08-04
电子制作(2018年12期)2018-08-01
中学数学杂志(2015年9期)2015-01-01
今日中学生(初三版)(2013年6期)2013-07-30

