2019年北京卷文科第19题的推广与变式

刘才华

(山东省泰安市宁阳第一中学 271400)

章建跃先生在《数学教育心理学》中提到:变式就是变更对象的非本质特征的表现形式，变更观察事物的角度或方法，以突出事物的本质特征，突出那些隐蔽的本质特征.这就要求教师在教学过程中，善于“借题发挥”， 一题多变，“以少胜多”,引导学生从不同的角度出发，对题目本身进行相应地理解以及挖掘，这对于提升学生的逻辑推理和数学运算等核心素养有着极大的帮助.下面对2019年北京市文科第19题进行推广与变式，供教学参考.

(1)求椭圆C的方程；

(2)设O为原点，直线l:y=kx+t(t≠1)与椭圆C交于两个不同点P,Q，直线AP与x轴交于点M，直线AQ与x轴交于点N.若|OM|·|ON|=2，求证：直线l经过定点.

将试题推广到一般的椭圆，我们得到如下

如果将命题1的条件和结论互换，我们得到如下

证明设P(x1,y1)，由椭圆的对称性得Q(-x1,-y1).

若将命题1中椭圆的上顶点换为右顶点，我们得到如下:

如果将命题3的条件和结论互换，我们得到如下:

仿照命题2的证明过程给出命题4的证明，过程从略.

若将命题3中的椭圆改为双曲线，我们得到如下:

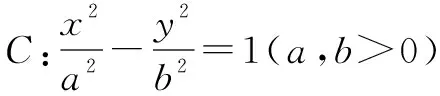
如果将命题5的条件和结论互换，我们得到如下:

仿照命题3、4的证明过程给出命题5、6的证明，过程从略.

如果将命题1中的椭圆改为圆，我们得到如下

命题7 设O为原点，直线l:y=kx+t(t≠b)与圆x2+y2=R2(R>0)交于两个不同点P,Q，A(0,R)为圆C与y轴的交点，直线AP与x轴交于点M，直线AQ与x轴交于点N.若|OM|·|ON|=R2，则直线l经过定点O.

如果将命题7的条件和结论互换，我们得到如下:

命题8 设O为原点，直线l:y=kx与圆x2+y2=R2(R>0)交于两个不同点P,Q，A(0,R)为圆C与y轴的交点，直线AP与x轴交于点M，直线AQ与x轴交于点N，则|OM|·|ON|=R2.

仿照命题1、2的证明过程给出命题7、8的证明，过程从略.