高考备考中天体运动问题的常考题型与解析(下)

李红红

(河北省邯郸市第四中学 056107)

在高三的复习备考中，可以将天体运动归纳为以下几种单知识点模型，通过对单知识点的深入理解来提高解决综合问题的能力.

模型一 星表模型

与环绕模型不同的是，星表模型主要研究星球表面上的物体随星球一起自转的运动.在这种模型下，又分为两种不同的情况，一是如果忽略星球自转因素的影响，则星球表面上物体所受的重力大小就等于星球对物体的万有引力的大小；二是如果不能忽略星球自转因素的影响，星球表面上物体随星球自转所需要的向心力由万有引力与星球表面对物体的支持力的合力来提供.

基本规律：星球表面物体绕星球一起自转，圆心在自转轴上.

图1

题型一：计算星球的质量及密度

例1 假设地球可视为质量均匀分布的球体，已知地球表面重力加速度在两极的大小为g0，在赤道的大小为g，地球自转的周期为T，引力常量为G.地球的密度为( ).

例2 在某行星和地球表面以相同的速率分别竖直上抛一个物体，它们各自返回抛出点的时间之比为1∶2，已知地球半径约为该行星半径的4倍，地球的质量为M，由此可知，该行星的质量为( ).

题型二：计算星球内部某处重力加速度

此题型源于2012年新课标卷的选择题，由星球表面的研究转移到到了星球内部的研究，或者可以认为由大家熟悉地研究“天上”转为研究“地下”；当然在转移研究的过程中，需要增加一个条件，那就是：已知质量分布均匀的球壳对壳内物体的引力为零.

图2

解答此题型的关键是根据题中的条件，将对星球内部某点重力加速度的求解，等效为一个新的星球表面重力加速度的求解.即：同一星球中心的不同半径的两个星球表面重力加速度的研究.所使用的基本公式均为：万有引力大小等于重力大小.以图2为例，星球表面A点与星球内部B点的重力加速度分别相当于半径为R和半径为r的星球表面重力加速度.

例3 (2012年新课标卷)假设地球是一半径为R、质量分布均匀的球体.一矿井深度为d.已知质量分布均匀的球壳对壳内物体的引力为零.矿井底部和地面处的重力加速度大小之比为( ).

特殊模型双星系统及多星系统

题型一 双星系统

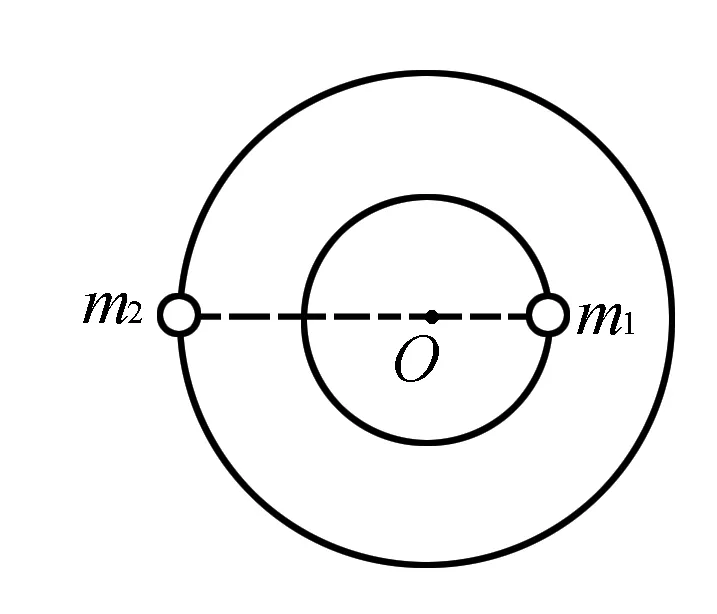
图3

双星系统：如图3，由两颗相距较近的恒星组成，每个恒星的线度远小于两个星体之间的距离，而且双星系统一般远离其他天体，在相互之间的万有引力作用下，绕连线上的O点做周期相同的匀速圆周运动.

基本规律：两星体间的万有引力提供向心力，且两星体公转周期和角速度都相等；

例4 双星系统是由两颗恒星组成的，在两者间的万有引力相互作用下绕其连线上的某一点做匀速圆周运动．研究发现，双星系统在演化过程中，两星的某些参量会发生变化．若某双星系统中两星运动周期为T，经过一段时间后，两星的总质量变为原来的m倍，两星的距离变为原来的n倍，则此时圆周运动的周期为( ).

解析双星靠相互间的万有引力提供向心力，具有相同的角速度，对两星列式：

题型二 多星系统

三星(或四星)系统：由三颗(或四颗)相距较近的恒星组成，在万有引力的作用下形成不同的稳定结构，绕其中某一星体或绕某一点做匀速圆周运动.

基本规律：所研究星体的万有引力的合力提供向心力；除中央星体外，各星体的角速度或公转周期相等，而各星体所受万有引力的合力因其在稳定结构中所处位置的不同会有所不同.

稳定的三星系统的存在形式：

①三颗质量相等的星体位于同一直线上，两颗环绕星围绕中央星在同一半径为R的圆形轨道上做匀速圆周运动，如图4甲所示；(注：图4甲中中央星体所受合力为0)

②三颗质量相等均为m的星体位于等边三角形的三个顶点上，均绕等边三角形的中心O做匀速圆周运动，如图4乙所示；

稳定的四星系统的存在形式：

③四颗质量相等的星体位于正方形的四个顶点上，沿外接正方形的圆形轨道运动，如图4丙所示；

④三颗星体始终位于正三角形的三个顶点上，另一颗位于正三角形的中心O点，外围三颗星体绕O点做匀速圆周运动，如图4丁所示；(注：图4丁中处于O点的星体所受合力为0)

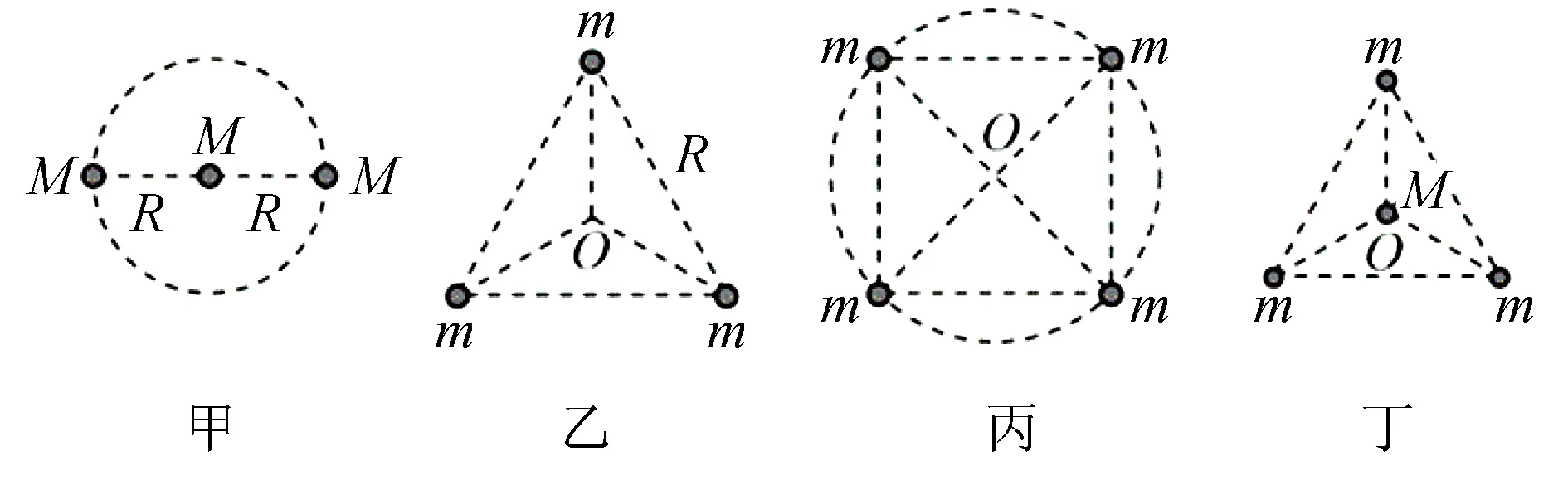
图4

同理可推知：稳定的五星或六星等多星系统的稳定存在形式.

例5 宇宙中有这样一种三星系统，系统由两个质量为m的小星体和一个质量为M的大星体组成，两个小星体围绕大星体在同一圆形轨道上运行，轨道半径为r，关于该三星系统的说法中正确的是( ).

A.在稳定运行情况下，大星体提供两小星体做圆周运动的向心力；

C.在稳定运行情况下，大星体应在两小星体轨道的中心，两小星体在大星体相对的两侧；

答案为C.

例6 由三颗星体构成的系统，叫作三星系统．有这样一种简单的三星系统：质量刚好都相同的三个星体a、b、c在三者相互之间的万有引力作用下，分别位于等边三角形的三个顶点上，绕某一共同的圆心O在三角形所在的平面内做相同周期的圆周运动，若三个星体的质量均为m，三角形的边长为a，万有引力常量为G，则下列说法正确的是( ).

A.三个星体做圆周运动的半径为a；

思维提炼

图5

从图5的“金三角”中，我们可以看到：环绕模型和双星模型用的是同样的研究思路①，即天体的运动形式为圆周运动，天体所受的万有引力提供向心力；而星表模型则主要是思路②，在不考虑星体自转的情况下，赤道上的物体所受的重力与万有引力大小相等；可见思路①主要研究“天上”的运动问题，思路②主要研究“地表或地下”的运动问题；而连接“天上”和“地表或地下”的桥梁就是“黄金代换式”.所以，对于天体运动问题的备考，我们都可以从上述的“金三角”中寻得模型及思路，使不同情境下的天体问题快速得到解决.