高中数学解题中圆锥曲线参数方程的应用研究

汤池武

(江苏省南京市宁海中学 210024)

高中数学圆锥曲线主要包括椭圆、双曲线、抛物线，三种曲线均对应有相关的参数方程.授课中做好参数方程知识讲解，使学生深入理解，并围绕具体例题讲解，使学生感受到应用参数方程解题的便利，养成使用参数方程解题的良好习惯，以获得事半功倍的解题效果，为其数学成绩的提升奠定基础.

一、椭圆参数方程在解题中的应用

分析该题目使用椭圆标准方程设出P点的坐标进行求解计算繁琐，容易出错.而使用椭圆参数方程，则可大大简化解题过程，提高解题效率.

在涉及到椭圆上点的问题时，可引导学生首先考虑采用参数方程进行解答，尽可能地少走弯路，如此才能更好地提高解题水平与效率.

二、双曲线参数方程在解题中的应用

分析题目中M为双曲线上任意一点，可考虑采用双曲线的参数方程进行求解.

解设M(asecφ，btanφ)，

所以平行四边形MAOB的面积

从中不难看出无论M点的位置如何，平行四边形的面积为定值.

该题目从常规思路解题计算量较大，另辟蹊径，采用参数方程可降低计算的繁琐度，实现快速求解，因此，日常教学中要求学生多加练习，积累双曲线参数方程解题的思路与技巧.

三、抛物线参数方程在解题中的应用

分析要求解抛物线的方程只需要求解出p的值即可.结合已知条件可考虑采用抛物线的参数方程进行解答.

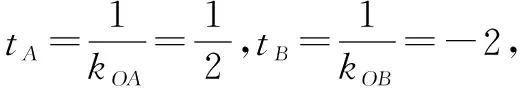
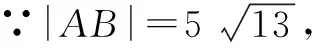
∴抛物线的标准方程为y2=4x.

运用抛物线参数方程经过简单的计算便可求出结果，因此，高中数学教学中，应注重做好学生学习引导，结合题干实际，灵活应用抛物线参数方程解题，不断提高解题效率.

圆锥曲线题型复杂多变，解题方法多种多样，尤其针对一些看似较为复杂的习题，应用参数方程求解往往柳暗花明，迅速得出结果，可很好地增强学生自信，因此，授课中为学生深入讲解圆锥曲线参数方程，使其搞清楚标准方程和参数方程的内在关联.同时，认真讲解相关例题，讲解参数方程具体应用，使其准确把握相关应用注意事项，促进其解题能力的明显提升.