不定期船连续航次燃油补给与航速优化集成调度模型
王春娟,陈 超
(山东交通学院国际商学院,山东威海264200)
0 引 言
不定期船运输在国际海上货运系统中占有重要地位.合理选择加油港、确定加油量和优化航段航速,对不定期船连续多个航次运营,不仅有利于降低运营成本、提高运营收益,还有助于控制运营时间、提高运营效率,从而提升船舶运营的整体质量.
与定期船航线不同,不定期船运营是一类航线涉及范围广、航次随机性大、航次衔接要求高的海上运输形式.近年来,随着海上远期运输合约的增加,不定期船运营规划涵盖的航次越来越多,在面对船用燃油价格持续高位、港口间燃油价格参差不齐时,船舶航次调度面临的问题也越来越复杂.加油港选择、加油量确定、载货量确定、航速设定等主要决策问题,不仅相互作用、相互耦合、相互制衡,共同决定着本航次的运营效益和效率,而且还连带影响和决定着后续航次的运营质量.如加油量与载货量,受船舶载货能力限制,对航次载货收益与耗油费用的效益悖反;如航段航速与燃油油价,对航次耗时成本与油耗费用的效用平衡.如加油港与加油量,受油价差异影响,对可能绕航加油产生的当下费用与后续获利的效益平衡.显然,解决这些问题不仅给不定期船的运营调度决策提出更高的要求,同时也提出严峻的挑战.
国内外学者关于不定期船运营调度的研究主要为:在燃油补给方面,贾鹏等[1]提出连续航次租船运营的燃油补给问题,构建以连续多航次收益最大为目标,以补给港和补给量为决策变量,基于燃油价格预测的非线性规划模型;MENG Q.等[2]研究了港口燃油价格不同情况下,货物选择对航次路径与燃油补给影响的联合优化问题.在航次航速方面,俞超等[3]、WEN M.等[4]、WANG C.等[5]分别就时间要求、算法设计、环境要求进行了研究.在综合调度方面,VILHELMSEN C.等[6]加入时间间隔限制的航次分离要求约束,研究经济航速下不定期船的路径优化、货物调度和燃油补给的集成调度问题;NORSTAD I.等[7]以总收益最大为目标,以每个航段的航速为决策变量,建立基于航速优化下的不定期船路径和调度模型.
与上述研究不同,本文关注不定期船连续航次运营调度面临的加油港选择、加油量确定、航段航速优化等诸多综合问题.针对这些问题的相互影响、相互作用、相互耦合关系,以及效益悖反和效应平衡关系,提出不定期船的连续航次燃油补给与航速优化集成调度问题,并将该问题视为一类非线性整数规划与效益悖反优化的复合问题.鉴于问题的属性和特点,提出集成调度、同步优化的解决思路,并创新地运用多重嵌套期望平均值处理技术与非线性整数规划建模方法,构建一个连续多个航次的船舶燃油补给与航段航速优化集成调度模型,开发设计了求解该模型的同步优化算法,并通过案例应用和对比分析,验证本文构建模型和算法的有效性、实用性和优越性.
1 问题描述
所谓不定期船连续航次运营调度,是指依据运输合同在规划与计划上确定运输任务与指派船舶后,在运作上对影响船舶运营效益与效率主要因素进行的决策活动.在船舶一个航次接着一个航次执行任务的过程中,航次路径构成通常为一个预备航段加上一个或多个载货航段.在此过程中,为提高船舶连续多航次运营的整体效益和效率,调度决策需要面对诸多影响因素.首先,选择加油港,补给低价燃油.加油港选择原则是,油价越低,越优先选择;加油港选择范围,不限于货物装卸港,可包含航线周边其他油价较低港口;这可能影响航次行驶路径,需要整体对比选择.其次,确定加油量.通常油价越低,加油量应越多,这样不仅可满足本航次需要,还可惠及后续航次;油价越高,加油量应越少,只限满足航次或航段需要即可;然而,受船舶载货能力限制,加油量过多,虽然利于降低船舶燃油费用,但也会减少船舶实载货量,降低航次收益.解决好这种收益与成本的悖反关系,需要对实货量与加油量进行约束.再次是,优化航速.油价较低时,航速可高一点,有利缩短航次时间,降低航次耗时成本,但航速较高,会加大燃油消耗,增加航次油耗费用;协调好航次耗时成本与耗油费用之间的平衡效应,需要构建航速与它们的反向增减函数进行制约.最后,确定船上存油价格.多个连续航次后船上的存油价格,已是多次剩油价格与加油价格的混合嵌套期望价格,准确确定存油价格将直接影响航段航速优化.因此,综合考虑以上决策内容间的相互作用、效益悖反和效应平衡关系,选取补给港口、补给油量、实载货量、航段航速为决策变量,以计划期内多个连续航次整体利润最大为目标函数,构建不定期船连续航次船舶燃油补给与航次航速集成调度模型.
2 模 型
2.1 模型假设
(1)各运输任务在时间上依次排序,不考虑受载期限制.
(2)不考虑船舶主机等要求的必备存油量下限.
(3)每个航次承运的货量可保证船舶满载,实载货量以船长宣载为准.
(4)船舶在任意港口的加油时间可忽略不计.
2.2 油价确定
关于船舶剩油价格核算,已有文献多采用上一次加油的油价进行计算[2].而产业界主要采用灵活的库存成本核算法.本文应用多重期望平均值处理技术进行核算.具体建模如下.
假设i,j为备选加油港编号;Rf(i,j)为i→j航段耗油的油价;Qf(i)、Rfr(i)为在i港舱内剩油量与油价;Qb(i)、Rfb(i)为在i港的加油量与油价.
那么,船舶在第1航段(1港→2港)消耗燃油的价格为
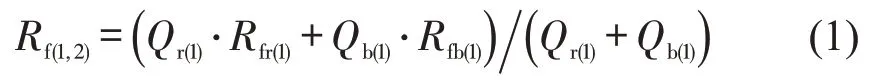
船舶抵达第2港后,船上剩油油价与第1航段消耗的油价相等,即Rfr(2)=Rf(1,2).
在第2航段(2港→3港)消耗燃油的价格为
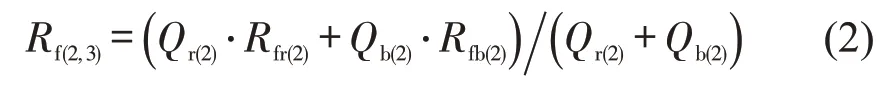
即

由此推导各航段船舶消耗的燃油价格为

船舶在i港的剩油价格等于船舶在i-1 →i航段的油舱内燃油价格,即

2.3 模型构建
设P为连续航次总利润;Ri,j为第i港至第j港运价;Xi,j为第i港至第j港船舶实载货量;Di,j为i→j航段的距离;Chr为船舶日租金;Npd为装卸港(不含绕航挂靠加油港)数量;Cprt为船舶在港使费;Vi,j为i→j航段平均航速;Qf(i,j)为i→j航段日耗油量;Yi为船舶在第i港加油量;Qfcap为船舶油舱总容量;QShcap为船舶载重吨;Vser为船舶服务航速;Qser为服务航速对应的日耗油量;Zk为0-1整数变量,k为路径方案;Xi,j、Yi、Zk、Vi,j为决策变量,则计划期内不定期船连续航次燃油补给与航速优化集成调度模型为

目标函数:式(6)表示连续航次总利润最大,各项分别为连续航次总收益、船舶租金总成本、燃油总成本和船舶在港使费总成本.约束条件:式(7)为燃油消耗量与速度关系函数,式(8)和式(9)表示各航段船舶燃油价格,式(10)为船舶在i港舱内剩余油量,式(11)为船舶油舱容积约束,式(12)为不超载约束,式(13)保证每次燃油补给量至少满足下一航段需要,式(14)为变量0-1整数约束,式(15)为船舶租金与载货能力关系函数,式(16)为非负约束.
3 实例分析
3.1 算例说明
某一航运公司现有一艘170 000 Mt(DWT)的散货船,油舱容量为5 000 Mt,服务航速为14.9 kn.在某一计划期内已签有3 单运输合同,分别为:①装→②卸、③装→④卸、⑤装→⑥卸,航线周边有可选加油港①'与②'.计划起始时,该船位于①港.连续航次路径如图1所示.
考虑可选加油港,此连续航次共有4种挂港方案,分别为:
方案1非绕航加油,即①→②→③→④→⑤→⑥.
方案2绕航①'港加油,即①→①'→②→③→④→⑤→⑥.
方案3绕航②'港加油,即①→②→②'→③→④→⑤→⑥.
方案4绕航①'港和②'港加油,即①→①'→②→②'→③→④→⑤→⑥.
分别对以上方案的备选加油港口进行顺序编号.以方案4为例,挂靠港口按照图2中1~8的顺序进行编号.
据安徽省水利工作会议消息,淮水北调工程已获安徽省内立项批准。淮水北调工程属南水北调东线安徽配套工程,也是皖北地区规模最大的跨区域调水工程。该工程自蚌埠五河站从淮河干流抽水,经淮北市濉溪县黄桥闸向北至宿州市萧县岱山口闸,调水线路总长266km,估算投资10.3亿元,主要保障淮北、宿州两市工农业生产用水。前期工作目前正加快推进,计划2012年4月底前完成可行性研究报告编制工作及部分泵站单体工程的初步设计,并报安徽省发改委批准,力争上半年开工建设。
3.2 基础数据
图3为各港口间海上距离与货运价格.设在①港时,船舱存油150 Mt,油价为450 USD/Mt,船舶租金为15 000 USD/d,各港口的港口使费均为40 000 USD.各港口燃油价格如表1所示.

图1 连续航次示意图Fig.1 Diagram of consecutive voyages

图2 备选加油港编号Fig.2 Numbers of alternative refueling ports

图3 各港间海上距离与货运价格Fig.3 Distances and freight rates between ports

表1 各港口燃油价格Table 1 Fuel prices at each port
3.3 算例结果及分析
(1)航线路径优化.
建立模型,利用LINGO 软件优化求解,对比4种方案的总收益、航段航速及燃油补给情况,如图4所示.
由图4可知,相比非绕航加油方案1、单独绕航方案2和方案3,方案4的总利润最大,最大可高出5.41×104USD.各方案优化的加油港和相应的加油量如图5所示.可见,为实现连续多个航次总利润最大,采用合理的燃油补给策略,不仅要考虑运输任务的装卸港口,还要考虑航线周边油价较低的港口,调整航线的最终行驶路径.同时,燃油补给决策还将影响船舶的航段航速与实载货量,使运营成本与整体收益达到有效平衡,具体如表2所示.
为进一步分析港口燃油价格、船舶租金、绕航距离及航段航速等因素变动对连续多个航次的总体效益影响作用关系,进行下列单项实验.

图4 优化的总利润对比Fig.4 Comparison of optimized total profits

图5 优化的加油港和加油量Fig.5 Optimized refueling port and volume

表2 优化方案各航段的航速与载货量对比Table 2 Comparison of speeds and cargo volume on each voyage of optimized schemes
(2)绕航加油港油价对优化结果的影响.
保持其他参数不变,调整备选加油港油价,测试油价变化对优化结果的影响,以①'港为例,结果如表3所示.

表3 绕航加油港油价变化对优化结果的影响Table 3 Influences on optimization results of oil price fluctuation
表3结果显示:当①'港油价增加40 USD 时,方案3 获得的连续航次总利润最大;当①'港油价减少60 USD 时,最优挂港方案为方案2;同时,备选加油港①'港的油价波动时,航次①→②的优化载货量发生变化,最优连续航次总利润也随之变化.可见,备选加油港油价波动变化将直接影响挂港顺序、加油港口与加油量、航段航速、实载货量等决策因素.
(3)船舶租金对优化结果的影响.
保持其他参数不变,调整船舶租金,测试船舶租金增减对优化结构的影响,结果如表4所示.
由表4可知:船舶租金越高,连续航次总利润越小;当船舶租金增加到50 000 USD时,方案3的连续航次总利润最大,即当船舶租金高到一定程度时,船舶将减少绕航加油;同时,船舶租金增加,各航段的优化航速都相应增加,导致船舶储备燃油量增加,最大载货量减少.由此可见,船舶租金波动将直接影响连续航次最大总利润,航次实载 货量和航段航速,以及加油港和船舶行驶路径.

表4 船舶租金变化对优化结果的影响Table 4 Influences on optimization results of changes of ship charter rates
(4)绕航加油航距对优化结果的影响.
在保持其他参数不变的条件下,调整可选加油港①'港与①港的距离,测试绕航加油距离变化对优化结果的影响,结果如表5所示.

表5 可选加油港航距对优化结果的影响Table 5 Influences on optimization results of distance changes to an optional refueling port
表5结果显示:当可选加油港①'与装货港①的距离增加90 n mile 及以上时,连续航次总利润最大下的最优方案为方案3;当此距离减少90 n mile 时,最优挂港方案为方案4;当此距离减少180 n mile 时,最优挂港顺序与减少90 n mile相同,但最大利润增加,①→①'航段的优化航速也有所增加,加油港口和加油量也相应发生变化.可见,绕航加油的航距不仅影响连续航次的总利润,同时影响相应的航段航速及燃油补给策略.
(5)经济航速与优化航速对比.
在调度实践中,航运企业通常采用经济航速指挥船舶运营.保持其他参数不变,取经济航速v=11 kn/h,测试经济航速与优化航速对优化结果的影响.表6为本文提出的优化航速与经济航速对比结果.

表6 优化航速与经济航速对优化结果的影响Table 6 Influences on optimization results of optimized speed VS economic speed
当选择经济航速时,连续航次总利润明显下降,与优化航速下连续航次总利润相比,降低了5.5×104USD.同时,加油量和载货量也受到相应影响,但选择的加油港口与最优挂港顺序保持不变.可见,本文构建的集成调度模型对航运生产实践具有一定的实用决策与指导作用.
4 结 论
针对国际船用燃油价格持续高企、不同港口燃油价格严重分化对不定期船运营产生的影响,本文构建集成调度模型.通过案例应用对比分析,研究结果表明,选择不同的燃油补给港和确定不同的燃油补给量,可有效平衡船舶实载货量与补给油量,实现多个连续航次的收益与成本控制;不同燃油价格下的航段航速优化,能有效平衡航次油耗成本与时间成本,从而实现不定期船多个航次的整体利润最大化.可见,本文提出不定期船连续航次燃油补给与航速优化集成调度问题具有一定理论研究价值.构建的集成调度模型能为不定期船连续多个航次航线运营提供决策参考.考虑到不定期船连续航次增加的动态性,未来可以研究滚动状态下不定期船连续航次燃油补给与航速优化集成调度问题.

