基于驾驶负荷的山区二级公路纵坡路段驾驶舒适度评价研究

胡立伟，殷秀芬，张苏航，范仔健，郭 治

(昆明理工大学交通工程学院，昆明650500)

0 引 言

随着西部大开发战略实施及脱贫攻坚行动向纵深发展，政府项目集中实现区域交通公平，山区公路里程不断增加.云贵山区由于地形地貌复杂，部分公路纵面起伏较大，易引发交通事故.研究发现，交通事故的产生是多因素协同作用的结果，驾驶员因素占主要原因.驾驶员在山区公路纵坡路段行车时，需集中精力、不断修正车速，适应道路线形不断变化，在此过程驾驶负荷不断变化.

国内外学者围绕驾驶负荷进行了大量研究，Maesden 等[1]指出，驾驶员生理指标可以准确反映技术人员的工作量，有效评估个人的驾驶负担.Chung[2]、Xuejian Kang[3]等利用脑电图(Electroencephalogram，EEG)分析研究驾驶员的驾驶负担；林声[4]、胡江碧[5]等将驾驶负荷用于研究高速公路，建立不同的驾驶负荷模型.关于山区公路驾驶负荷的研究较少，阎莹等[6]通过驾驶人在不同坡度和弯坡组合段的实车试验，分析下坡路段纵坡坡度与车速、心率关系并以此建立回归模型；徐进等[7]通过对山区复杂公路开展自然驾驶实验，研究分析汽车驾驶人心率增长率与加(减)速度、公路纵面线形参数的相关关系.

综上，现有研究主要基于心生理特征、操纵行为等研究高速公路驾驶工作负荷，关于山区低等级公路驾驶负荷的研究较少；且大多研究只分析相关关系，难以反映驾驶员驾驶舒适度.本文选取云南省文都二级公路，分析驾驶负荷与各参数间的关系，建立模型并分析驾驶舒适度阈值.

1 数据采集

1.1 实验道路

选择云南省文都山区公路作为研究对象，试验路段为双向2车道，沥青混凝土路面的山区二级公路，设计时速40 km/h，平均纵坡坡度4.2%，极限值7%.其中，K0～K97.334段，全长97.334 km，弯多坡急，地势险要，事故频发.考虑外界条件，如道路状况、气候条件等均会对试验产生一定干扰，为最大化保证试验准确性，排除天气、超车、会车等干扰，选择文都山区公路K70+000～K90+380 典型路段进行实车试验，路段标志标线清晰，视距良好，车流量适中.试验天气多云，温度适宜，光线良好，路面干燥，共试验4 d.表1为试验路段基本参数.

表1 试验路段基本情况参数Table 1 Basic information of test section

1.2 实验人员

为保证实验数据有效性和可靠性，减少驾驶员差异性对实验的影响，招募驾驶员并初步筛选，尽可能避免焦虑、激进型驾驶员.最终选取年龄25～40 岁，驾龄为5年及以上的男性驾驶员15 名.被试驾驶员驾驶技能熟练，驾驶习惯良好，身体机能正常，被试前一天生理状态较好.

1.3 实验设备

试验车型选用大众朗逸，车内装有行车记录仪用以记录试验全过程；心率检测仪采用MP150生理记录仪，此外，选用V-BOX数据采集系统用以测量车速及行驶距离.

1.4 数据采集

对试验路段进行反复试验，每个驾驶员以平均车速35 km/h进行试验，间断试验7次，往返1次约75 min，每次试验后休息15 min.15 名驾驶员同时开始测试，分4 d 完成，每天试验约3 h.采集上、下坡路段各105组数据，数据分析及建模使用上坡路段87 组数据，下坡路段85 组，其余数据用于模型验证.采集数据如下：

(1)速度数据.持续采集车速，考虑实际山区公路等级普遍较低，地形复杂，车速变化较频繁，行驶条件较差，速度难以反应真实行驶状态，本文选用加(减)速度指标.

(2)生理信号数据.采集驾驶员生理信号数据(心率).

(3)纵坡路段特征参数数据.

2 山区二级公路纵坡路段驾驶负荷表征研究

2.1 驾驶负荷表征

本文从驾驶员视角入手，以行车时驾驶员的心率增长率表征驾驶负荷.其中，心率增长率以最小心率为基准，其为纵坡路段驾驶员行车过程中平静状态下所测得.驾驶负荷值越高表明驾驶员越紧张，驾驶越不舒适，反之亦然.驾驶负荷计算公式为

式中：HHRI为纵坡路段行车过程中驾驶员的心率增长率(驾驶负荷)；HRmax为纵坡路段驾驶途中驾驶员心率最大值(次/min)；HRmin为纵坡路段驾驶途中驾驶员心率最小值(次/min).

2.2 驾驶负荷水平划分

利用SPSS 对上坡、下坡路段实测得到的心率增长率HHRI、纵坡路段车辆加(减)速度a、纵坡路段坡度i、坡长l指标进行多元正态分布检验，输出结果如表2所示.

表2 路段数据正态性检验Table 2 Normality test of section data

因数据样本数n＜100，故选用Shapiro-Wilk统计量.分析正态性检验结果的显著性值可知，纵坡路段各项数据均满足正态检验(显著性值大于0.05).

Cafiso 等[8]研究表明，当一个安全评价指标满足正态分布时，则表明该指标的第50、第85分位值可用于划分路段安全水平的阈值.本文借鉴此方法，利用心率增长率HHRI指标第50和第85分位值划分驾驶负荷水平及驾驶舒适度，如表3所示.

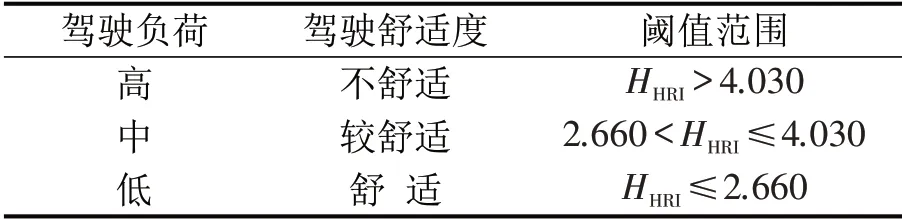
表3 驾驶负荷水平划分表Table 3 Division of driving load level

3 相关性分析

3.1 纵坡路段关键指标对驾驶负荷的影响

将坡度、坡长及加(减)速度分别与心率增长率指标进行回归分析，并对比分析三者对驾驶负荷影响的显著性.

(1)上坡路段.

①对加速度ac与驾驶负荷曲线进行拟合发现，线性回归R2较高，F检验值最大，拟合最优，表达式为

②同理，坡度i与驾驶负荷二次曲线关系拟合表达式为

③坡长l与驾驶负荷线性回归拟合表达式为

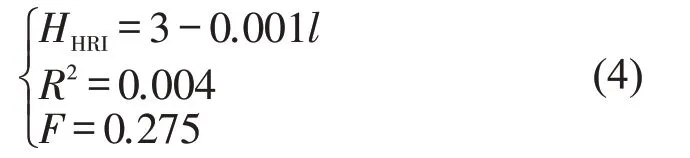
(2)下坡路段.

①减速度ab与驾驶负荷线性回归拟合较好，表达式为

②坡度i与驾驶负荷二次曲线关系拟合表达式为

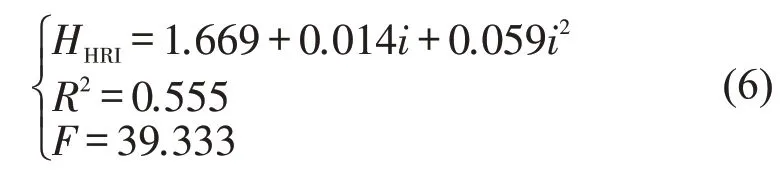
③坡长l与驾驶负荷线性回归拟合表达式为

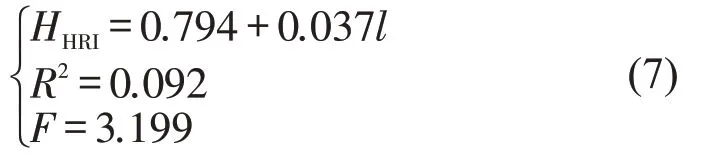
分析式(2)～式(7)可知，坡度i对纵坡路段驾驶负荷为显著变量，上坡坡度产生显著正向影响，下坡坡度产生显著负向影响；加(减)速度a对上、下坡路段驾驶负荷皆会产生显著正向影响；坡长l对上、下坡路段驾驶负荷的影响均很小，进一步对坡长与驾驶负荷相关关系进行分析.

3.2 纵坡坡长与驾驶负荷相关关系分析

(1)基于坡度阈值的山区二级公路纵坡坡长对驾驶负荷影响(二维影响关系分析).

根据文都山区公路道路设计资料，公路坡度在1%～7%，集中在4%左右，故将坡度分为低于等于4%和高于4%两组，以有效避免因坡度变化太大造成影响.

①坡度i≤4%.

在此坡度范围内，根据测试仪器收集的驾驶员心率数据，计算在实验纵坡路段行驶时的驾驶负荷值.当坡度i≤4%时，上、下坡路段坡长与驾驶负荷的相关关系如图1所示.

图1 坡度i≤4% 时坡长与驾驶负荷相关关系Fig.1 Correlation between slope length and driving load when i≤4%

②坡度i＞4%.

在测试路段，当纵坡坡度大于4%时，驾驶相对困难，行车风险较高.坡度i＞4%时，上、下坡路段坡长与驾驶负荷相关关系如图2所示.

图2 坡度i＞4% 时坡长与驾驶负荷相关关系Fig.2 Correlation between slope length and driving load when i＞4%

分析图1和图2可知：当坡度i≤4%时，无论上坡还是下坡，坡长与驾驶负荷都仅存在弱相关性；当坡度i＞4%时，坡长与驾驶负荷相关性有所增加，但仍呈弱相关，即坡长增加，驾驶员心率变化趋势较弱.此外，下坡路段坡长对驾驶负荷影响较上坡更大，这可能是因为下坡路段行车，驾驶员需频繁制动，驾驶操纵量增加，负荷增大.故驾驶员在下坡路段行车时更应谨慎行驶.

(2)坡度与坡长组合指标对驾驶负荷的影响(三维影响关系分析).

①上坡路段.

图3为上坡路段坡度、坡长组合与驾驶负荷关系.

图3 上坡路段坡度、坡长组合与驾驶负荷关系Fig.3 Relationship between slope,slope length and driving load of uphill section

分析图3可知，整体来看：随坡长增加，驾驶负荷有轻微增加的趋势，但相较坡度而言，该趋势较小.此外，当坡长l在100～200 m，坡度i在4%～7%范围内，驾驶负荷较高；当坡长为150 m，坡度为6.03%时，驾驶负荷增幅最大，这可能是因为在受限行车条件下，随着坡度增大，车辆行驶阻力增加，驾驶人为保持车辆行驶稳定性，需持续施加脚操纵量，使驾驶负荷增大.

②下坡路段.

图4为下坡路段坡度、坡长组合与驾驶负荷关系.

图4 下坡路段坡度、坡长组合与驾驶负荷关系Fig.4 Relationship between slope,slope length and driving load in downhill section

分析图4可知，整体来看：在坡长100～200 m，坡度4%～7%范围内，驾驶负荷较高；随着坡度不断降低，受益于纵断面线形指标改善，驾驶负荷有较明显的下降态势.

对比分析上、下坡路段坡度坡长组合与驾驶负荷关系，下坡坡长对驾驶负荷影响更大，但与坡长相比，驾驶员对坡度变化更加敏感.综上，驾驶员在山区公路纵坡路段行车时，坡长变化对驾驶负荷产生一定影响，总体来看坡长增加会引发驾驶负荷增大，但这种影响不明显，故本文忽略坡长影响，构建纵坡路段驾驶负荷模型为

4 山区二级公路纵坡路段驾驶舒适度评价

以山区公路纵坡路段坡度及加(减)速度为自变量，以心率增长率为因变量，表征驾驶负荷，采用多元线性回归分别建立上、下坡路段驾驶负荷模型.

4.1 上坡路段驾驶舒适度评价

(1)上坡路段驾驶负荷模型.

上坡路段驾驶负荷参数估计结果如表4所示.

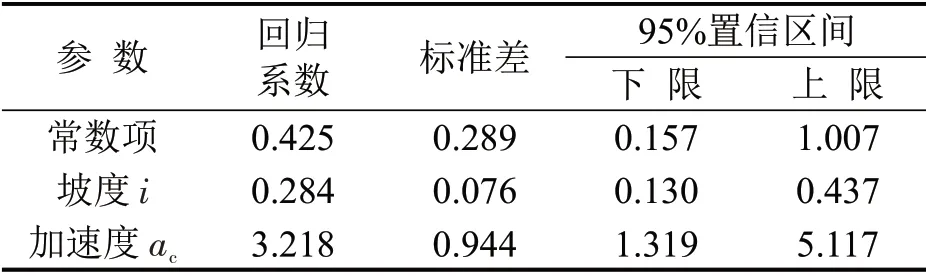
表4 上坡路段驾驶负荷参数估计结果Table 4 Parameter estimation results of driving load on uphill section

上坡路段驾驶负荷模型最终解释度R2为0.609，即加速度、坡度可以较好地解释驾驶负荷变化.上坡路段驾驶负荷模型为

(2)上坡路段驾驶舒适度阈值分析.

根据表3，绘制山区公路上坡路段加速度、坡度与驾驶舒适度关系，如图5所示.

图5 上坡路段驾驶舒适度Fig.5 Driving load comfort on uphill section

4.2 下坡路段驾驶舒适度评价

(1)下坡路段驾驶负荷模型.

表5为下坡路段驾驶负荷参数估计结果.

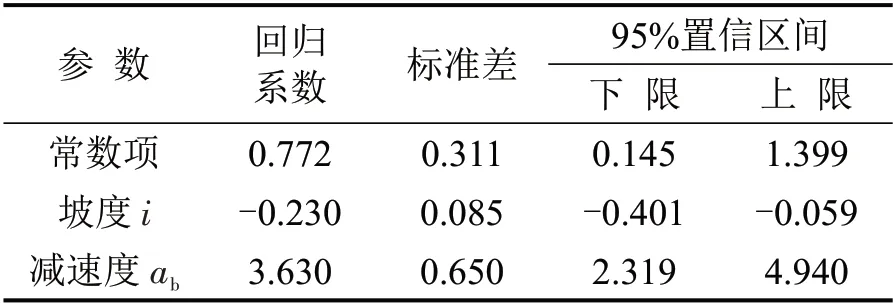
表5 下坡路段驾驶负荷参数估计结果Table 5 Parameter estimation results of heart rate growth rate in downhill section

下坡路段驾驶负荷模型最终解释度R2为0.738，即减速度、坡度可以解释驾驶负荷73.8%的变化原因.下坡路段的驾驶负荷模型为

(2)下坡路段驾驶舒适度阈值分析.

同理，下坡路段坡度、减速度与驾驶舒适度关系如图6所示.

图6 下坡路段驾驶舒适度Fig.6 Comfort of driving load on downhill section

对比分析上、下坡路段驾驶负荷舒适度发现，坡度相同时，下坡路段驾驶员产生不舒适感的可能性更大，行车危险性更大.

5 实例应用分析

5.1 模型验证

对比分析试验实测驾驶负荷数据及计算数据，验证模型合理性.数据分为计算组和试验组，试验组数据不包括建模所用数据.筛选样本数据上坡18组，下坡20组.对比上、下坡路段实测驾驶负荷及模型计算值，如图7和图8所示.

由图7和图8可知：模型精度较高，可较好地反映实际山区公路纵坡路段行车过程中驾驶负荷变化情况，此外，下坡路段模型精度要高于上坡路段.

图7 上坡路段实测驾驶负荷与模型计算值Fig.7 Comparison of measured data and model calculation data of uphill section

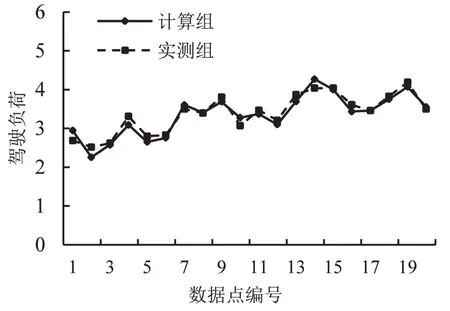
图8 下坡路段实测驾驶负荷与模型计算值Fig.8 Comparison of measured data and model calculation data of downhill section

5.2 驾驶舒适度阈值验证

以文都公路K84+520～K90+380 段为例，全长5.86 km，考虑篇幅，本文仅对下坡路段驾驶负荷舒适度阈值分析验证.筛选下坡路段数据如表6所示.同时根据云南省公安厅交通警察总队提供的2017—2019年云南文都山区二级公路K84+520～K90+380路段交通事故分布如表7所示，结合本文对下坡路段驾驶舒适度的阈值划分，评价K84+520～K90+380路段驾驶舒适度情况.

表6 山区公路下坡路段数据Table 6 Data of downhill section of highway in mountainous area

整理分析2017—2019年云南文都山区二级公路K84+520～K90+380 路段交通事故资料，共23起.结合图6下坡路段驾驶舒适度图分析可知：下坡路段坡度达到最大(7%)时，减速度需小于0.46 m/s2才能保证驾驶舒适度在较舒适范围内；否则驾驶负荷增大，易引发交通事故.纵坡路段坡度与加(减)速度值的增加会引发驾驶负荷升高，同时验证了基于驾驶负荷对山区公路纵坡路段驾驶舒适度划分阈值的客观性与合理性.

6 结 论

本文基于实车试验，划分驾驶负荷舒适度，分析山区二级公路纵坡路段坡度、坡长及加(减)速度对驾驶负荷的影响，坡度及加(减)速度对驾驶负荷影响均显著，而坡长影响较小，据此进一步通过控制坡度阈值分析坡长对驾驶负荷的影响及坡度坡长组合共同对驾驶负荷的影响，构建山区二级公路纵坡路段驾驶负荷模型并进行驾驶舒适度阈值划分，结合实例验证了基于驾驶负荷对山区公路纵坡路段驾驶员驾驶舒适度评价的合理性，可为实际工程应用提供一定参考.

表7 山区公路下坡路段事故分布数据Table 7 Traffic accident distribution data of downhill section of mountain highway

本文构建纵坡路段驾驶负荷模型时，仅考虑了坡度坡长及加(减)速度3个指标，下一步研究中将加入其他道路特征参数及车辆运行特征参数.