考虑居住区位的公共交通出行行为分析模型

钟异莹，陈 坚*,2，邵毅明，李 睿

(1.重庆交通大学交通运输学院，重庆400074；2.重庆大学建筑城规学院，重庆400044)

0 引 言

随着我国城市化进程的快速发展，城市人口与日俱增，城市居住空间发生着巨大变化，从而对人们出行活动产生一定影响.近年来，城市交通需求持续高于供给，导致交通拥堵日益严重，呈现出空间上向中、小城市漫延，时间上向平峰扩张的趋势.优先发展公共交通已成为社会各界的普遍共识，探索不同居住区位下的公共交通出行方式选择影响机理，是城市规划、社会、交通等多学科研究的重要课题.

许多学者构建土地利用属性、社会经济属性、家庭属性与出行行为之间的定量分析模型，其中，居住空间区位与出行行为相互作用机理研究主要集中在两个方面：一是土地利用与交通一体化研究，二是基于活动导向的出行需求分析.前者聚焦于居住地或工作地的位置与交通出行选择间的一体化，即土地利用与交通需求之间的关系，忽略选择行为过程中的影响因素分析；后者强调个人活动或居住区的微观因素对出行决策行为的潜在影响.WANG 等[1]指出居住环境决定社会环境，从而对人际交往和活动出行行为产生巨大影响；吴娇蓉等[2]建立个体行为MNL 模型，研究居住区公共设施的规划布局对居民出行偏好的影响；NURLAELA等[3]在行为分析框架内刻画居住在公共交通附近的居民选择行为和出行方式之间的多维关系；COEVERING 等[4]利用潜变量模型解释出行者根据居住环境与出行态度调整出行决策的过程；ETMINANI-GHASRODASHTI 等[5]利用结构方程模型分析不同居住区位下居民出行选择的差异性.既有研究中，探讨个体水平上的居住区位与出行相关变量之间结构关系，强调个体间的差异性，验证不同社会经济属性对个人出行选择的影响，忽略了数据存在嵌套结构的特点，有群体特征属性但只能在个体水平测量的变量并不能通过群体直接得到，需要通过聚集居民个体评价分数才能形成，因此，个体水平与群体水平变量结构关系的差异性亟待进一步验证.

本文基于计划行为理论和群体动力学理论，从出行者个体心理层面和居住社区层面两个维度分析出行决策行为，构建考虑居住区位的公共交通出行多水平结构方程模型，为优化居民出行结构提供理论依据.

1 影响变量选取

1.1 变量选取

多水平结构方程模型(Multilevel Structural Equation Model，MSEM)分析包含组内模型和组间模型的拟合，需要构建个体(组内)水平和组群(组间)水平潜变量.为探讨不同层面上居住区位对公共交通出行行为的影响，基于计划行为理论，选取个体水平潜变量为：行为态度、主观规范、知觉行为控制、行为意向和居住区位.组群水平潜变量指组内不变、组间可变的变量，为解释组间变异，构造行为态度、居住区位、行为意向的组群水平潜变量.变量定义和说明如表1所示.

表1 变量描述Table 1 Description of variables

1.2 研究假设

计划行为理论中，个人对事物的信念、人格特质等外部因素决定行为态度、主观规范及知觉行为控制，而行为态度、主观规范及知觉行为控制将影响行为意向.基于计划行为理论，在个体水平上提出假设：行为态度、主观规范及知觉行为控制之间存在相互影响关系，行为态度、主观规范及知觉行为控制对行为意向均有正向的直接影响.

居住区位与出行选择行为的相关研究中，居住区位对行为态度、主观规范及行为意向造成不同程度的影响，VOS 等[6]认为，居住在郊区的出行者比居住在城市中心的出行者的出行态度积极；尹超英等[7]验证了居住地的空间建成环境越完善，居民选择公共交通通勤的可能性越高.在居民个体水平上提出假设：居住区位对行为态度、主观规范、知觉行为控制及行为意向均有正向的直接影响.

群体动力理论认为，一个人的行为，是个体内在需要和环境外力相互作用的结果，用于论述群体中的各种力量对个体的作用和影响.本文认为，出行者的出行行为是其出行内在需求(行为态度)与客观出行条件(居住区位)相互作用的结果.在社区水平假设：行为态度与居住区位间存在相互影响作用关系，行为态度对行为意向有正向的直接影响，居住区位对行为意向有正向的直接影响.模型框架如图1所示：下标W 表示组内变量，下标B表示组间变量，+表示正向影响；部分变量间存在双向的交互影响，用双向箭线表示.研究假设如表2所示，不作假设验证.

图1 模型框架Fig.1 Model framework

表2 研究假设Table 2 Research hypothesis

2 模型构建

2.1 数学模型

MSEM通过各构念多指标测量并以潜聚合方式形成高水平构念的设置，可以视作结构方程模型(Structural Equation Modeling，SEM)的拓展，为体现组群水平随机效应，允许某些系数矩阵在不同组群之间变化.基于变量选取与模型假设，构建考虑居住区位的公共交通出行多水平结构方程模型，包括：测量模型、组内结构模型、组间结构模型3部分.

(1)测量模型.

式中：i为个体指标；j为组群标记；Yij为16×1 维观测变量向量；vj为16×1维的截距向量；λj为16×5维对5个潜变量的因子载荷矩阵；ηij为5个潜变量的5×1维向量；Kj为5个外生协变量Xij对16个观测变量Yij回归斜率构成的16×5维矩阵；Xij是5个观测协变量构成的5×1维向量；εij为16×1维残差向量，假定服从均值为0，协方差矩阵为的多元正态分布.

(2)组内结构模型.

式中：αj为5×1维截距项向量；Bj为组内潜变量之间关系的5×5 维结构回归系数矩阵；Γj为组内潜变量对外生变量回归斜率系数的5×5 维矩阵；ζij为5×1 维潜变量回归残差向量，假定服从均值为0、协方差矩阵为Ψ的多元正态分布.

(3)组间结构模型.

式中：ηj为组间3个潜变量的3×1维向量；μ为3×1维截距项向量；β为组间潜变量之间关系的3×3维结构回归系数矩阵；γ为组间潜变量对外生变量回归斜率系数的3×3维矩阵；Xj为组间3个观测协变量构成的3×1维向量；ζj为3×1维潜变量回归残差向量，假定服从均值为0、协方差矩阵为Ψ的多元正态分布.

MSEM中，矩阵和Ψ中元素假定不随组群变化，含有模型参数的矩阵，包括：vj、αj、λj、Kj、Bj、Γj，即可以固定，也可以在组间变化.

2.2 分析步骤

(1)确定分组变量.包括：个体层面与组层面的潜变量及其测量变量，将受试者分成若干组，确定分组数量.

(2)数据检验.计算分组情况下各变量的组内一致性ICC(1)、组间一致性ICC(2)和共识程度rwg，检验哪些变量存在组群效应.

(3)根据步骤(1)、步骤(2)的分组与变量选择结果，提出研究假设，构建不同水平上的模型框架，确定各变量间的关系.

(4)利用Mplus 做MSEM 分析.包括：路径系数或载荷系数的显著性，各参数与预设模型的关系是否合理，各拟合指数是否通过，根据MI 指数调整模型至最优.

(5)模型解释.根据输出结果结合问卷题项进行解释，探索各变量间的相互作用发生在组内还是组间.

3 实例分析

3.1 数据检验

以重庆市主城区居民为研究对象，选取龙湖两江新宸、渝能国际、民心家园等不同区位，不同规模的30个居住区，于2019年6月进行调查.主要通过街道办下发问卷，进行随机调查和交叉控制配额抽样调查，回收有效问卷3 107份(每个社区平均100 份左右).被访者包含不同社会经济属性类型居民，样本整体上具有较好的代表性.问卷共设计21个题项，涉及居住区位、主观规范、行为态度、行为意向、知觉行为控制，问卷回答采用李克特5级量表形式，按“非常同意”“同意”“一般”“不同意”“非常不同意”分别赋值5～1分.

为检验变量是否存在组群效应，计算所有变量的ICC(1)、ICC(2)和rwg值，其中，主观规范、知觉行为控制未通过检验，居住区位、行为态度、行为意向对应测量变量的检验值如表3所示.

ICC(1)值均大于0.059，表明题项在个体间有一定程度的相关，即变量存在足够显著的组间差异；ICC(2)值均大于标准值0.700，表明同一个社区内居民评价均值作为社区特征的评价具有可信性；rwg值均大于经验值0.700，表明可以将居民个体评估分数聚集到社区水平.因此，通过聚集居民个体评估的居住区位、行为态度、行为意向分数在社区内部具有高度的一致性，3 个潜变量存在组群效应，适合做多水平分析.

表3 变量检验指标值Table 3 Test indexs value of variables

3.2 模型评价与修正

利用Mplus 计算模型，模型拟合采用MLR 方法进行参数估计，结果如表4所示.

所有测量变量的载荷系数均大于0.600，显著性检验均达到0.010，平均方差抽取量均大于标准值0.500，组合信度均大于标准值0.600，表明居住区位、行为态度、主观规范、知觉行为控制、行为意向5个潜变量的测量变量选取合理，各测量变量个体水平上和社区水平上均能够较好的反映潜变量构念，且社区水平的测量效果优于个体水平.

假设可以通过各潜变量之间的标准化路径系数值进行验证，其中，“知觉行为控制←居住区位”的路径系数较小，临界比值小于标准值1.960，显著性检验未通过，表明该路径不显著，H7 不成立.其余8 条路径显著，对应假设因果关系成立.假设验证结果如表5所示.

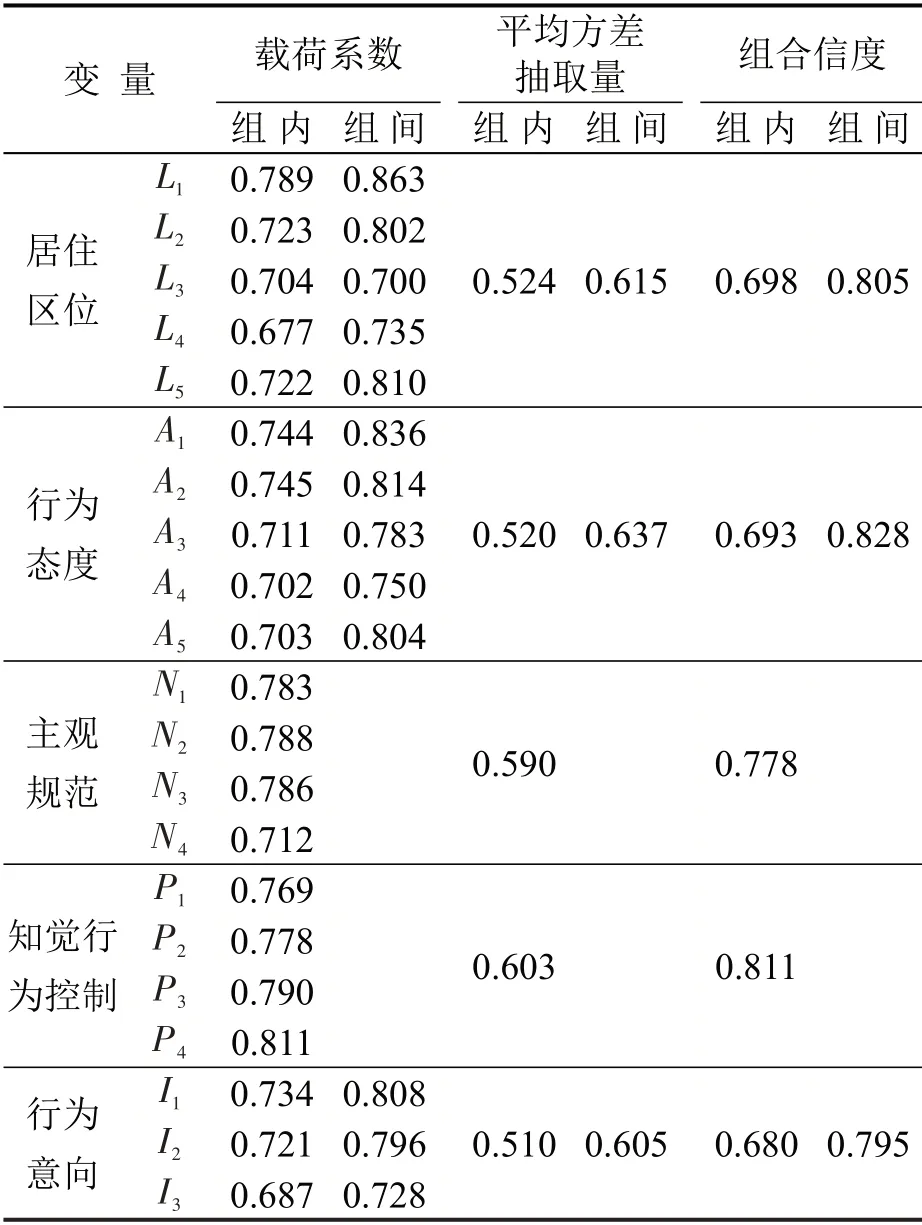
表4 模型参数估计Table 4 Model parameters estimation

表5 假设验证结果Table 5 Results of hypothesis test

删除不显著路径，重新拟合模型后各项参数均通过检验，调整后拟合指标CFI、TLI大于标准值0.900，RMSEA、SRMR-Within、SRMR-Between 均小于标准值0.080，模型在个体、社区水平上拟合效果均良好，结果如图2所示，其中，变量间连线上的数字表示路径系数.

图2 模型结果Fig.2 Model results

3.3 模型解释

对比单水平和多水平结构方程模型参数发现，某些变量的显著性有所不同.“行为意向←行为态度”路径系数表现为社区水平大于单水平大于个体水平，行为态度无论在何种情况下均对行为意向有正向的显著影响，且在社区水平上表现的最明显；“行为意向←居住区位”路径在社区水平上最为显著；“行为意向←主观规范”路径在个体水平上比单水平模型的显著性更高；其余的路径系数相差不大.从输出的拟合指数来看，MSEM拟合情况要优于SEM，但是组间模型拟合相对较差，模型参数对比如表6所示.

表6 模型参数对比Table 6 Comparison of model parameters

SEM与MSEM中不同变量对行为意向的影响效应存在一定差异，如表7所示.

表7 影响效应对比Table 7 Comparison of influence effects

SEM中，居住区位对行为意向直接影响最小，但其是唯一对行为意向有间接影响的变量，总效应值最大，各影响变量总效应由大到小依次为：居住区位、行为态度、知觉行为控制、主观规范.MSEM 组内方程中，仅有居住区位对行为意向有间接影响，各影响变量总效应由大到小依次为：居住区位、主观规范、行为态度、知觉行为控制.MSEM 组间方程中，仅有居住区位与行为态度对行为意向有直接影响，无间接影响，其中，影响效应为行为态度大于居住区位.

4 结 论

本文以居民公共交通出行选择为研究对象，基于计划行为理论构建个体层面包含心理影响因素的理论框架，结合群体动力理论提出社区层面的群体选择行为关系模型，深入探索居住区位对公共交通出行选择行为的影响机理，得出以下结论：

(1)在居民公共交通出行选择研究中，将居住区位与出行心理影响因素纳入模型是必要的.

(2)在建构理论模型时，关键的问题之一是在某个水平上概念之间的关系是否能够在另一个水平上复制，当研究变量数据存在嵌套结构时，单水平模型便不再适用于该问题的研究.多水平结构方程模型克服了传统单水平模型只能对独立个体分析的局限性，分别从个体水平和社区水平对公共交通出行选择影响进行分析，得到社区水平上的变量测量效果优于个体水平.

(3)模型着重分析了个体与群体间的差异，但没有对不同群体作对比，后续可针对不同群体间的出行决策规律做进一步研究.