一道中考题的解法探究

摘要：在数学的学习中，学生分析问题和解决问题的能力是十分重要的。教师在日常的解题教学中，应注重引导学生如何思考。对于有多种解法的题进行方法归纳，一题多解有利于培养学生从不同的角度分析问题，从而提高学生的学习能力。

关键词：解题教学;方法归纳;学习能力

教师最重要的任务之一是帮助学生学习。这个任务并不很容易，它包含了时间、实践、奉献和正确等因素。

著名数学家波利亚认为，我们的解题工作应该分为四个阶段：理解题目，拟定方案，执行方案，回顾。这些阶段中的每一个都有其重要性。

一、 题目呈现

（2021年江苏省连云港市中考数学第16题）如图，BE是△ABC的中线，点F在BE上，延长AF交BC于点D。若BF=3FE，则BD/DC=___________。

二、 解题实践

（一）理解题目

本题是一道几何题，已知条件是BE为中线且BF=3FE，未知量是BD/DC的值。隐含的条件有对顶角相等，即∠AFE=∠BFD。

（二）拟定方案

第一个角度，从题目的两个条件入手的话，关于中线，我们知道中线将三角形的面积分为相等的两部分，其次是构造中位线以及通过倍长中线构造全等三角形;关于另一个条件BF=3FE，易得BF/FE=3，由线段的比值可想到相似比，从而可想到构造相似三角形，另外，对于同高或者等高的两个三角形，面积之比等于相应的底边之比，故可得S△ABF=3S△AEF，所以这道题也可以考虑从面积入手。

第二个角度，如果从题目的结论入手，关于求线段的比值，仍然可构造相似三角形或者找到相应的等高或同高的三角形等，线段之比便是相应的底边之比，进而转化为三角形的面积之比。

第三个角度，换一个解题环境，将几何问题代数化——建立平面直角坐标系，通过建立适当的坐标系，设点的坐标，将BD、DC的长表示出来，再求BD/DC。

基于以上思考，笔者拟定了以下解题方案：

1. 尝试构造两个相似的三角形，使得BF、FE、BE中的某两条成为这两个三角形的一组对应边;

2. 等倍延长中线BE，构造全等三角形，同时也构造了相似三角形;

3. 尝试构造两个相似的三角形，使得BD、DC、BC中的某两条成为这两个三角形的一组对应边;

4. 将线段之比转化为相应的三角形的面积之比;

5. 以B为坐标原点，BC所在的直线为x轴，过B点且垂直于BC的直线为y轴，建立平面直角坐标系。

（三）执行方案

思路1：构造含有BF、FE、BE中某两条线段的相似三角形。

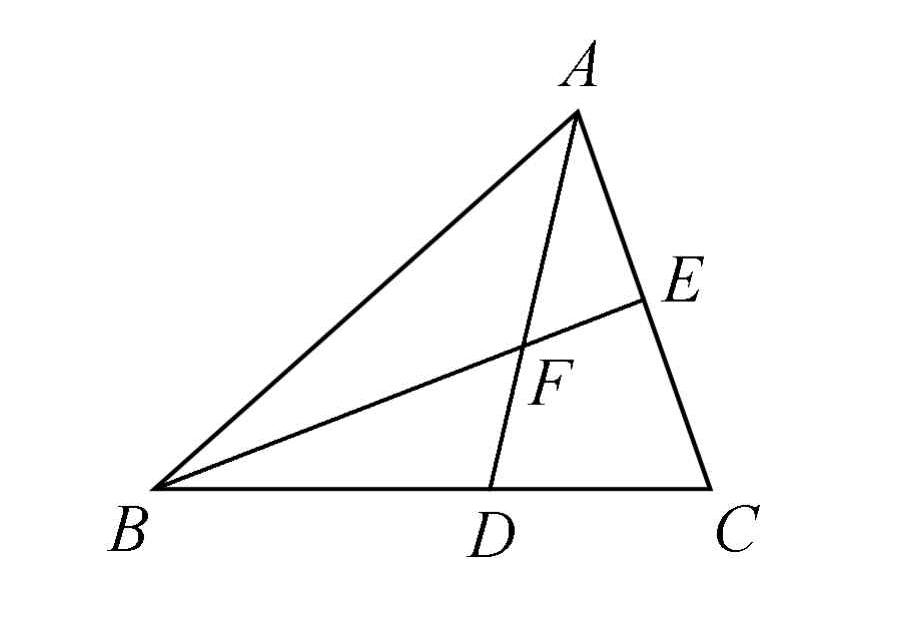
解法1：如图1，过点E作EG∥BC交AD于点G，得△EFG∽△BFD，则EGBD=EFBF=1/3，故BD=3EG，又因为EG∥BC，所以△AEG∽△ACD，则EG/CD=AE/AC=1/2，故CD=2EG，所以BD/DC=3/2。

解法2：如图1，取CD的中点H，连接EH，得EH是△ACD的中位线，故EH∥AD，则△BDF∽△BHE，所以BD/DH=BF/EF=3，又因为CD=2DH，所以BD/DC=BD/2DH=3/2。

思路2：等倍延长中线BE，构造全等三角形，同时构造相似三角形。

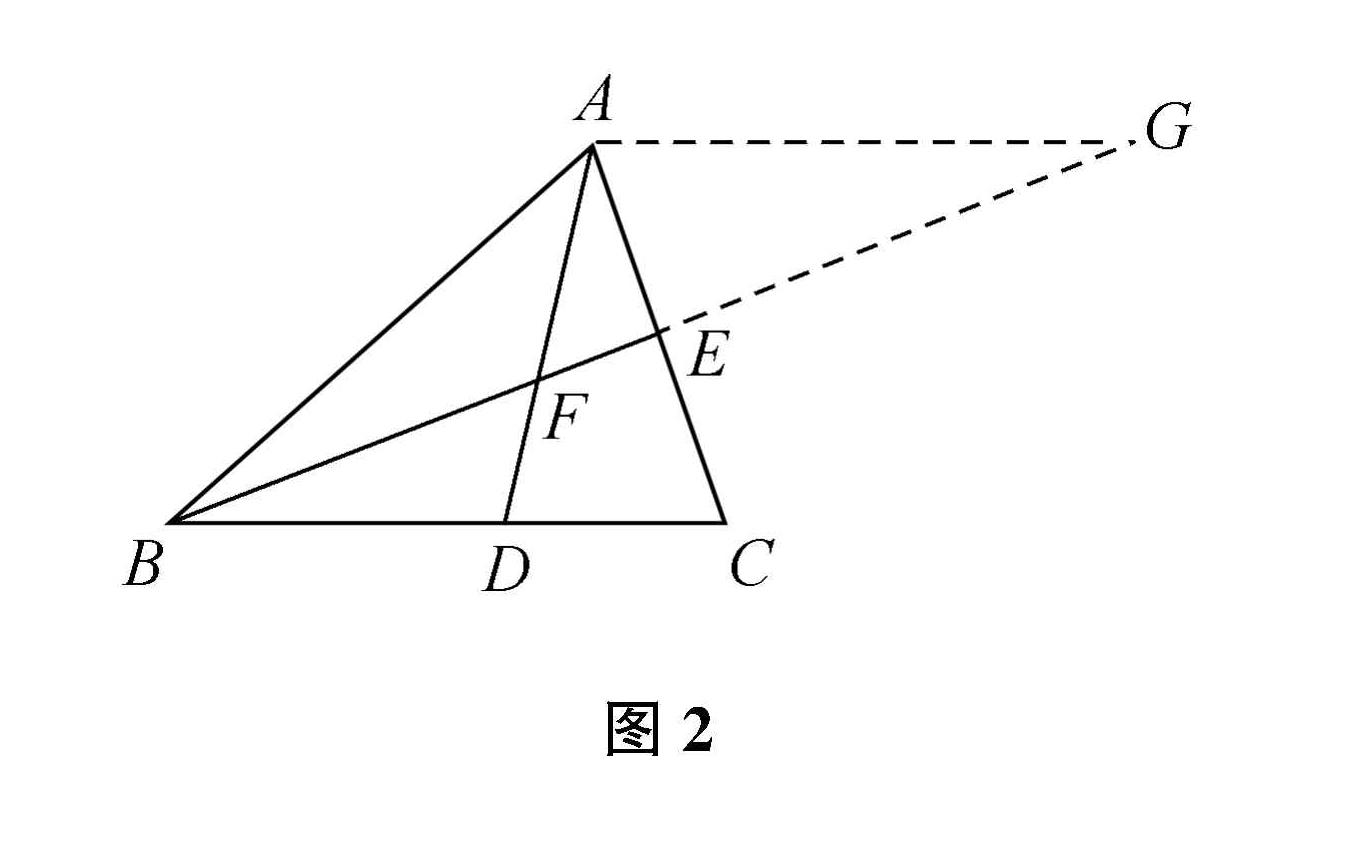
解法3：如图2，延长BE至点G，使得EG=BE，连接AG，得△AEG≌△CEB，则AG=BC，∠G=∠CBE，所以AG∥BC，从而得△AFG∽△DFB，所以AG/BD=FG/BF，因为BF=3FE，所以FG=EG+EF=BE+EF=5EF，故AG/BD=5/3，所以BC/BD=5/3，因而BD/DC=3/2。

思路3：构造含有BD、DC、BC中的某两条线段的相似三角形。

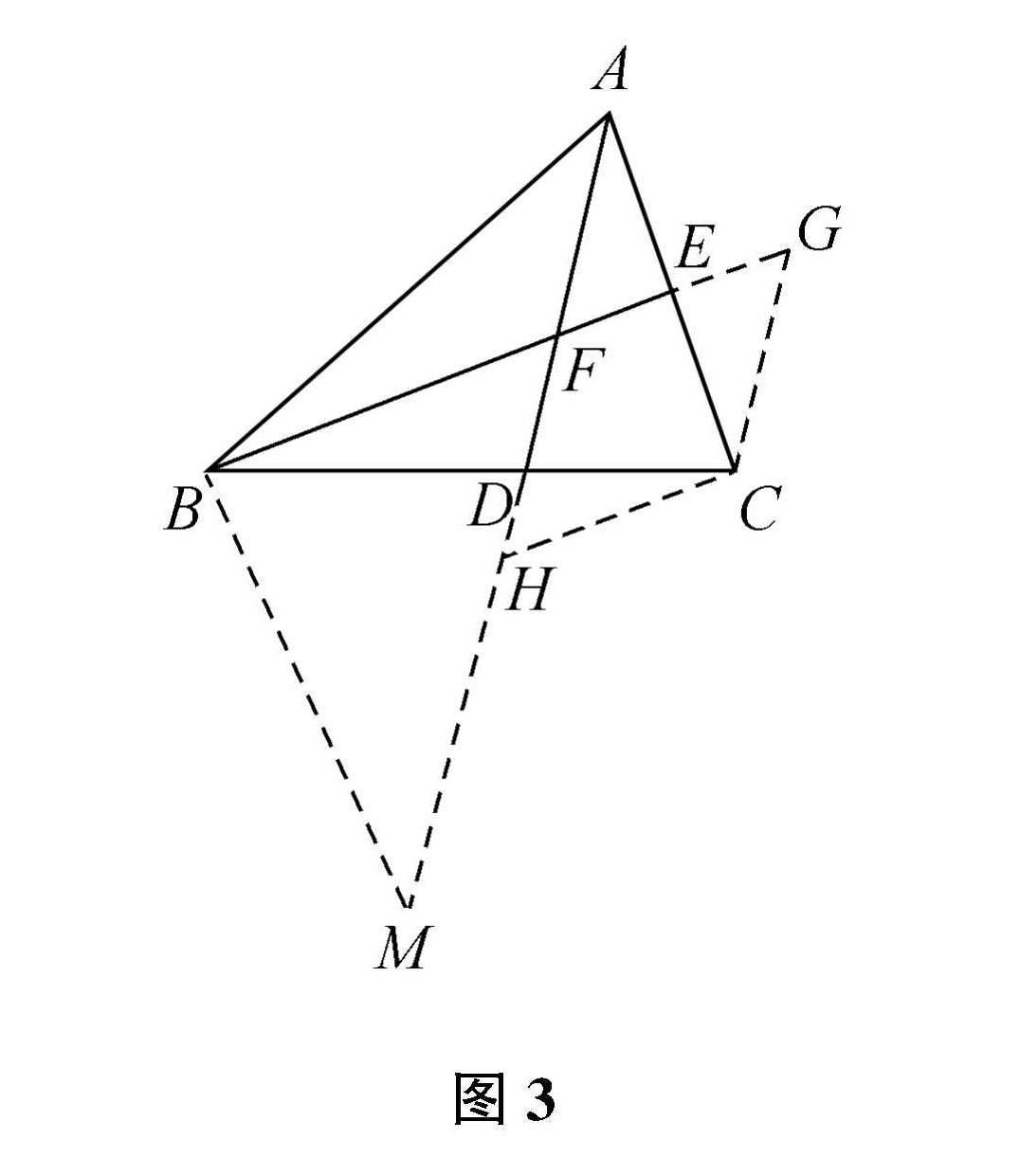
解法4：如图3，过点C作CG∥AD交BE的延长线于点G，得△AEF≌△CEG，则EF=EG，所以FG=2EF，又由CG∥AD得BD/DC=BF/FG=3/2。

解法5：如图3，过点C作CH∥BE交AD的延长线于点H，得△AEF∽△ACH，则EF/CH=AE/AC=1/2，故CH=2EF，又由CH∥BE得△BDF∽△CDH，所以BD/DC=BF/CH=3/2。

解法6：如图3，过点B作BM∥AC交AD的延长线于点M，得△AEF∽△MBF，则BMAE=BFEF=3，由BM∥AC亦可得△BDM∽△CDA，所以BD/DC=BM/AC=BM/2AE=3/2。

思路4：将线段之比轉化为相应的三角形的面积之比。

解法7：如图4，连接DE，设S△AEF=x，S△DEF=y，因为△ABF和△AEF同高，所以S△ABF∶S△AEF=BF∶EF=3∶1，所以S△ABF=3S△AEF=3x，同理可得S△BDF=3y，因为DE是△ACD的中线，故S△ACD=2S△ADE=2x+2y，因为S△ABD=S△ABF+S△BDF=3x+3y，且△ABD和△ACD同高，所以BD/DC=S△ABD/S△ACD=3/2。

解法8：如图4，连接CF，由解法7得S△ABF=3S△AEF，因为E是AC的中点，故S△AEF=S△CEF，所以S△ABF∶S△ACF=3∶2，因为△ABD和△ACD同高，所以BD/DC=S△ABD/S△ACD，同理可得BD/DC=S△BDF/S△CDF，所以BD/DC=S△ABD/S△ACD=S△BDF/S△CDF，故BD/DC=（S△ABD-S△BDF）/（S△ACD-S△CDF）=S△ABF/S△ACF=3/2。

思路5：建立平面直角坐标系。

解法9：

（四）回顾与反思

关于这道中考题，在求解的过程中，我们应该先理解题目，理清已知量、未知量及隐含条件，并探究已知量和未知量之间的联系。经过探究，笔者一共找到了9种解法，回顾这9种解法，核对每一个步骤。完成解题任务后，我们应及时回顾反思。整道题的重要条件是BF=3FE，相当于已知线段的比值。在我们的学习中，相似三角形这一章节是会涉及线段的比值的，即相似三角形的相似比。不论是从条件出发还是从结论出发，都体现了线段的比值，所以构造相似三角形是比较容易想到的方法，而构造相似三角形的方法是不唯一的，基本可以分为两大类，从条件出发构造相似三角形或者从结论出发构造相似三角形。

另外，我们也知道两个三角形如果是同高的，那么三角形的面积之比便等于相应的底边之比，而本题中有同高的三角形，因而这道题还可以从面积的角度入手。

关于第9种解法，这是一种完全不同的思路。虽然这种解法对于这道题来说，不是最简便的方式，比较烦琐，对运算能力要求较高，但它体现了几何问题代数化以及几何问题坐标化的思想，也体现了“设而不求”的思想，同样能解决本题，并且它在其他的一些问题中是可以有一定的优势的。如果就本题而言，本题更适合用构造相似三角形或者用面积的方法。

同一道题目，不同的解法，体现了不同的思路，让我们能更好地理解题目，积累解题经验，避免造成思维固化，也有利于培养学生分析问题和解决问题的能力，逐渐做到减负增效，让学生更轻松地学习，提高学生的学生兴趣。

参考文献：

[1]G·波利亚.怎样解题[M].上海：上海科技教育出版社，2011.

作者简介：

李洁，江苏省苏州市，吴江区松陵第一中学。