基于VaR-GARCH模型的我国商业银行汇率风险度量的分析研究

冯媞 谢斌斌 侯俊屹 董子腾

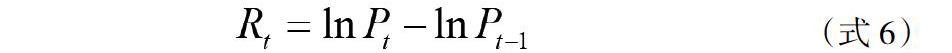
摘 要：在浮动汇率制下，汇率风险的管理对于我国商业银行经营的稳定性至关重要，而对汇率风险管理的前提是能对汇率风险进行准确的度量。从现阶段来看，我国商业银行的汇率风险管理还处于比较落后的阶段，因此对汇率风险进行准确识别与有效度量是我国商业银行仍需解决的难题。本文选取我国金融市场的部分日汇率中间价，在理论分析和实证研究的基础上运用VaR-GARCH方法度量我国金融市场的汇率风险，最后得出在GED分布下的GARCH（1，1）模型是最优的度量五种汇率风险的模型，且运用VaR方法度量我国商业银行汇率风险是必要且可行的。

关键词：VaR-GARCH模型;汇率风险;商业银行;风险管理

一、研究背景及意义

风险度量是汇率风险管理的主要流程之一，在风险管理中起着重要的作用，它是风险识别的延续，也是正确处理和控制风险的依据。我国商业银行的汇率风险管理注重风险控制，但商业银行的风险管理整体起步较晚，而偏技术性的风险度量更为其薄弱环节。

目前我国大部分银行以敞口分析和敏感性分析为主，若要更好的控制风险则需要从定性分析转化为定量分析，且我国对于外汇衍生工具的运用还没有很普遍，外汇期货和期权交易市场不完善，商业银行内部审计方法存在缺陷，缺乏横向和纵向的相互制约，管理人员掌控风险的能力较弱，不能制定出科学有效的风险管理策略，这些都在一定程度上限制了商業银行汇率风险的转移和规避。

控制汇率风险的前提是准确的度量汇率风险，本文将选取我国2012年到2019年的部分外汇数据，通过运用VaR-GARCH的方法对我国商业银行的汇率风险进行度量，并在理论分析的基础上进行实证研究，为引入VaR作为我国商业银行汇率风险的度量工具提出可行性建议。

二、模型介绍

1.VaR方法

VaR方法即Value at Risk，称为风险价值模型，在现代金融风险管理中是最核心和基本的度量方法，它的产生是由于传统的ALM和CAPM无法准确定义和度量金融风险。G30集团在研究衍生品种的基础上于1993年发表的报告《衍生产品的实践和规则》中提出了VaR方法。VaR模型中风险的测量是建立在概率论与数理统计的基础上，具有很强的科学性且统一了风险计量标准。金融机构在仅有一个具体的指标数值——VaR的情况下就可以粗略地得知整个金融机构或投资组合的风险状况，这使得金融机构各业务部门对有关风险信息的交流更加便捷，最高管理层也能够随时掌握机构的整体风险状况及时进行风险调控，因此VaR方法常被金融机构用来进行风险管理。

“在正常市场环境下，给定一定概率水平（也即置信度），用于测度预期某一金融资产或证券组合在未来特定的一段时间内的最大可能损失的方法”，这是菲利普·乔瑞对VaR权威的解释，用数学公式可表示为：

2.GARCH模型

GARCH模型被称为广义ARCH模型，是ARCH模型的拓展。ARCH模型实质上是使用残差平方序列的q阶移动平移对当期异方差函数值进行拟合，而移动平均模型具有自相关系数q阶截尾性，因此ARCH模型只适用于异方差函数短期自相关过程。但在实践中会有一些残差序列的异方差函数具有长期自关性，此时若仍使用ARCH模型对异方差函数进行拟合，不仅将会产生很高的移动平均阶数，使参数估计的难度增加，还会影响ARCH模型的拟合精度。因此为解决这一问题，Bollerslev提出了广义自回归条件异方差模型，即GARCH模型，模型简记为GARCH（p，q）。

GARCH模型是在ARCH的基础上又考虑了异方差函数的p阶自回归性，可以更有效拟合具有长期记忆性的异方差函数，反映实际数据中的长期记忆性质。因此我们可以通过建立误差项的方差和均值模型更加准确对波动性进行分析与预测。

三、实证研究

1.样本数据选取及说明

目前，我国大部分的商业银行计算VAR以持有期一天为标准，因此本文采用日VaR进行分析。鉴于美元、欧元、日元、港币、英镑几种货币是我国主要的贸易结算货币，而且是我国外汇储备的主要构成部分，本文选取了直接标价法下，美元、欧元、港币、日元、英镑兑人民币的日汇率中间价（数据来源于国家外汇管理局网站）。数据选取区间为2012年1月4日到2019年12月31日。

相比一般收益率，几何收益率具有很好的统计特征，更适合进行金融建模，同时在金融研究中人们更关注收益率和价格变动而不是价格本身，因此本文借助Eviews和Excel对原数据序列先取对数，将其汇率的价格序列转化为对数收益率序列lnPt，再进行一阶差分处理，最后得到几何收益率Rt。

2.样本数据检验分析

日收益率序列并不符合传统的正态分布，而是呈现“尖峰厚尾”;GED分布下的GARCH（1，1）模型可以更好地拟合模型的波动集群现象，从而使测算VAR的结果更加科学合理。

日收益率序列一般都呈现尖峰厚尾的状况，不符合传统的正态分布，收益率的分布则直接影响VaR的计算精度，因此在进行模型拟合前我们需要先对数据进行正态性检验。本文将先采用J-B检验来对五种外汇收益率序列的正态性进行检验，再采用GED分布或t分布来代替正态分布，这样尾部的拟合效果和度量精度就得到了提高。

（1）J-B检验及其他统计特征

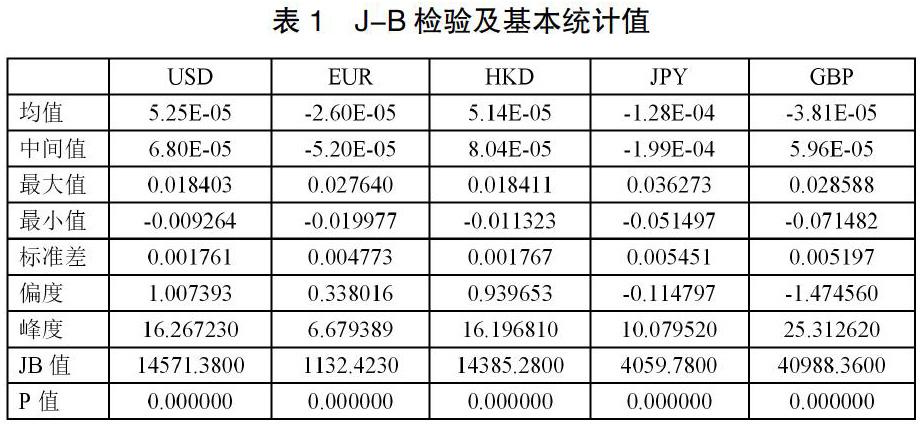
对于收益序列的正态分布特征的检验，我们运用eviews对五种汇率进行J-B检验。假设J-B统计量服从正态分布，若P<0.01则在1%的显著性水平下可以拒绝原假设，即序列不服从正态分布;否则接受原假设，认为服从正态分布我们根据运行结果把美元、欧元、港币、日元、英镑的收益率序列基本统计值绘制成表1。

从表1中可以看出，五种汇率的偏度都不为0，其中美元、欧元，港币的偏度大于0，收益率分布有右拖尾现象;日元、英镑的偏度小于0，收益率分布有左拖尾现象。同时五种汇率的峰值都显著的大于3，说明其收益率序列分布都比正态分布更集中呈现出“尖峰”的状态。而从JB统计量来看，所有的P值都为0，因此序列不服从正态分布。通过对偏度、峰度和JB统计量进行分析，发现收益率序列呈现尖峰厚尾的现象，不符合正态分布。因此本文将采用t分布，GED分布来描述各序列的尖峰厚尾现象，以更好刻画尾部特征，提高VaR的度量精度。

（2）平稳性检验

时间序列的平稳性是对时间序列进行研究的首要前提，且GARCH模型只适用于平稳性序列，因此此处采用ADF检验，对美元、欧元、日元、港币、英镑的收益率序列Rt进行平稳性检验。

检验结果得出：五种外币收益率序列的ADF检验值在1%、5%、10%的显著性水平下均小于临界值，所以通过了平稳性检验，因此美元、欧元、日元、港币、英镑的收益率序列均不存在单位根，是平稳的时间序列。

（3）自相关检验

Q统计量是由Ljung和Box于1978年提出，用来检验一系列自相关性是否具有统计显著性，本文通过对扰动项进行自相关检验来证明扰动项是否自相关。各收益率序列的Q统计量检验结果如表2所示。

本文取的滞后阶为8，从表中可以看出，在5%的显著性水平下，欧元和英镑Q统计量所对应的P值均大于0.05，因此可以接受原假设，我们认为收益率序列是不相关的。当Q统计值逐渐增大时，人民币汇率正在逐步走向白噪声，此时的收益率序列符合随机游走过程，但是由于美元、日元和港币的收益率序列均存在自相关，因此在对这三种外汇收益率建立回归方程时需要加入滞后项来消除自相关。

（4）异方差检验

由于回歸函数中存在异方差容易引发多重共线性问题，因此我们需要检验收益率序列分布来判断回归函数是否具有条件异方差，本文采用ARCH效应对收益率序列进行异方差检验。

根据ARCH效应检验我们可看出在滞后阶数为8时，ARCH统计量的P值均小于0.01，因此原序列存在高阶的ARCH效应，我们可以采用GARCH（p，q）模型下的VaR方法来度量汇率风险。

（5）GARCH模型滞后阶数的选择

由于模型GARCH（p，q）通过了异方差检验，本文将运用该模型对波动性进行估计。GARCH（1，1），GARCH（2，1），GARCH（1，2）和GARCH（2，2）均是实验中常用的GARCH模型，所以我们在GED分布和t分布的前提下，根据AIC和SC准则确定出模型的最优滞后阶数。

根据得出的AIC值和SC值，美元、欧元、港币、日元与英镑五种的收益率数据在滞后阶数为（1，1）时的AIC值和SC值的偏差都较小。若AIC值和SC值差别不大，我们则选取滞后阶数少的模型，这样可以降低待估参数的个数，方便计算，因此GARCH（1，1）模型最合适。

（6）模型的残差检验

在确定使用GARCH（1，1）模型后，我们对模型的残差序列进行ARCH-LM检验。根据美元、欧元、港币、日元与英镑收益率的t分布和GED分布表可见，在1%的显著性水平下，模型所对应的P值均大于显著水平，因此模型的残差序列不存在ARCH效应，所以模型能够很好地反映美元、欧元、港币、日元与英镑五种汇率收益率序列的异方差性。

四、结论与政策建议

本文通过VaR-GARCH模型对我国商业银行汇率进行度量，并采用t分布和GED分布刻画收益率序列的尖峰厚尾现象，最后结合实证研究得出结论：

以2012年1月4日到2019年12月31日的汇率数据来看，VaR方法度量我国商业银行汇率风险效果较好，可以便捷准确地显示出某段时间内我国商业银行汇率的风险水平，且分析得出日收益率序列表现出较为显著的“尖峰厚尾”特征，不符合传统的正态分布;其次，通过实证分析，我们发现GED分布下的GARCH（1，1）模型可以更好地拟合日收益率序列分布存在的“尖峰厚尾”特征，从而使测算VaR的结果更加合理。因此，运用VaR方法度量我国商业银行汇率风险是必要且可行的。

2005年以前，我国实行的是人民币盯住美元的汇率政策，商业银行面临的汇率风险较低，因此对汇率风险的识别与度量意识淡薄。2005年汇改之后，汇率波动更加频繁。在这个变幻莫测的金融环境中，监管部门和商业银行的管理者需要能够对汇率风险进行更可靠更准确地度量，因此必须选取能准确反映资产收益波动的模型对于度量商业银行的汇率风险是极其必要的，这也为我国的金融风险管理提供一个良好的技术保证。

对于商业银行，应选取适合自身的、拟合程度较好的分布来建立模型，以便更好地度量风险，同时长期监控汇率风险，应对极端情况。因为各种因素反映在汇率上是长期的，且是叠加性的，所以建立实时的监控处理系统能够更高应对风险。VaR方法作为西方商业银行主流的度量汇率风险的工具，我国也可以结合自身经济形势进行运用，有效控制汇率风险，减少汇率风险带来的损失。

参考文献：

[1]何倩.我国商业银行汇率风险度量的实证研究[D].苏州大学，2014.

[2]张琳.不同阶段下我国商业银行汇率风险度量的实证研究[D].广西师范大学，2016.

[3]龚妮.GARCH模型与VaR在外汇风险度量中的应用[J]，长安大学学报，2006，109（6）：22-26.

[4]陆红.基于VaR-GARCH族模型的我国商业银行汇率风险度量研究[D].东北大学硕士学位论文，2010.

[5]朱沛，孙英隽.我国商业银行汇率风险研究——基于VAR-GARCH模型的实证分析[J].中国物价，2018（11）：34-36.

[6]李竞晖.提高城商行利率风险管理能力的研究[D].西南财经大学，2018.

[7]李卓娜.我国商业银行汇率风险实证研究[D].南京航空航天大学硕士学位论文，2012.

[8]杨文艳.我国商业银行外汇风险度量的实证研究——基于改进的VaR方法的应用[D].苏州大学，2009.