提升初中学生数学素养的三步棋
张建珍

【摘要】学生学习数学的过程就是提升自身素养的过程,也是让自己不断适应社会的过程.因此,教师在教学过程中,要聚焦学生的成长特点,让他们的素养在各个方面都得到提升.具体地来说,提升素养就要着力培养学生的质疑能力、自主能力、合作能力.有了这些能力,素养就能得到良好的发展.
【关键词】初中数学;数学素养;三步棋
当前初中数学教学的落脚点还多处于学生现阶段的发展情况,而没有对他们的长远发展做一个规划,换言之,数学教学没有着眼于学生的长久发展.教师关注更多的是哪一道题目不会做,哪一个细节出了差错.其实,数学教学可以从更广的视角去建构教学,即发现学生在哪些思维能力上有欠缺,需要提升哪些方面的素养等.放眼未来,才能让学生的素养生长有底气.
一、拓展思维,培养学生的质疑能力
学生在学习数学时最缺的就是质疑的习惯.曾经做过问卷调查,调查家长跟子女聊学习时说得最多的一句话是什么,大多数家长写的是有不会的题目要去问老师.可现实的状况是,学生基本不去问老师.一方面,学生在作业上出现的差错,教师会在评讲中给予解答,因而他们觉得没有必要去问;另一方面,教师没有给学生问问题的时间与机会,渐渐地他们也就不问问题了;还有就是学生在学习上缺乏主动性,不会去质疑,不会将学习推向纵深.因此,教师要鼓励学生质疑,让他们自己去发现新的认知中存在的问题,进而在解决问题的过程中使自身的素养得到提升.
培养学生质疑的能力对教师来说要分成三步.首先,要给学生一定的时间,让他们去发现问题.大多数学生不是没有疑问,而是发现不了问题.教师要给他们思考的时间,让他们在阅读数学文本的过程中,将新旧认知对比,将前后信息对比,以发现可疑之处.大多数数学教师总把课堂安排得满满的,多少时间讲解,多少时间做题都有一个大致的盘算,但也应盘算出留多少时间让学生去探究、去内化,即去发现问题.其次,给学生设定一定的问题,让他们带着问题去思考,在思考的过程中他们自然就会生出新的问题.这个生出问题的过程就是质疑的过程.
以华师大版九年级上册一元二次方程的解法(公式法)为例,预习时教师让学生学着去问问题,有了问题,他们自然会将探索的触角伸向远处.学生第一个问题就是有了配方法为什么还要学习公式法.这个问题看似与真正的数学问题无关,却是学生心里的一个真实的反应.教师说,每一个方法都有它的优点,也有它的缺点.教师让他们灵活运用各种方法,以最优的方式解答问题.学生在预习导学案的开始部分看到这样的表述:已知ax2+bx+c=0(a≠0)且b2-4ac≥0,它的两个根为x1=-b+b2-4ac2a,x2=-b-b2-4ac2a.学生立刻就提出问题:“这个公式可以用配方的方式推出来吗?”教师让学生自己试一试.学生又有了这样的疑问:“配方法怎么用的?”于是学生先想问题,再想方法,将原方程式先移项,得ax2+bx=-c,接着学生将二次项系数化为1,得x2+bax=-ca.再接着学生将两边加上一次项系数一半的平方就得出了x+b2a=±b2-4ac2a.可见,在质疑的过程中学生的思维是不断向前推进的.
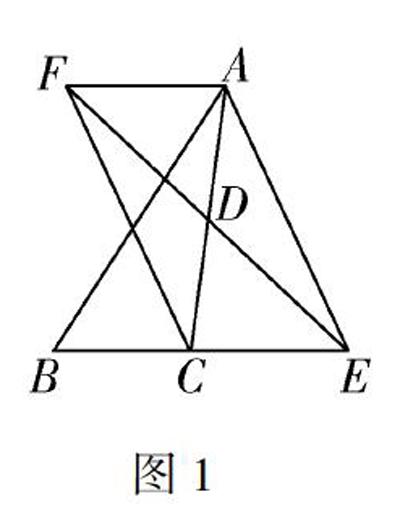
图1让学生去问问题,是培养他们质疑能力的有效方式.但对学生来说让他们发现问题有時候比较困难,除了教师的引导,也要让他们借助图形,有了直观的感知,才能更容易冒出新的问题.以华师大版八年级数学下册矩形的判定为例,教师设置这样的题目,在△ABC中,D是AC的中点,点E在BC的延长线上,过点A作BE的平行线与ED的延长线交于点F,连接AE,CF.如果AC=EF,那么会出现怎样的结论.这其实就是让学生去发现问题,对于抽象的文字,学生要做的第一步就是将它转化为图形.学生根据文本的表述,作出图1.
有了具体的图形,学生再将文字与图形进一步对接,于是有了这样的问题:四边形AFCE是什么形状.就着具体的图形,学生很快就有这样的疑问,四边形AFCE是不是一个矩形?有了质疑接着就是要化解疑问.首先,学生从已知条件中获取到AF平行于CE,AC=EF,也就是一组对边平行,对角线相等.学生将可能有的结论与已知条件对接起来,发现要判定这个四边形是矩形只要证明AF和CE 相等就可以了.对于AF和CE 是否相等他们又生出许多问题.两个线段相等,如果在同一个三角形中,就要证明是不是等腰三角形或者等边三角形,如果在不同的三角形中就要看是不是全等三角形.有了这样的质疑,他们就锁定了△ADF和△CDE,因为已知AD=CD,∠ADF=∠CDE,AF∥BE,因此就轻松得出两个三角形全等的结论,进而得出AF=CE.明显地,就着图形更容易发生质疑,思维更容易被激活.
二、养成习惯,培养学生的自主能力
初中学生在数学学习上缺乏自主性,大多数学生都需要由教师支配着学习的时间与方式,在数学上他们几乎没有自己的主见.其实就素养的培养来说,教师要尽可能地培养他们的自主能力.同样,曾经就初中的学生做过一次调查,第二天要讲解圆与直线的关系,教师在放学时却没有布置家庭作业,结果班上没有一个学生主动去预习的.从这件事来看,至少说明现在的学生在自主学习上还有很多需要强化的地方,需要不断地去修正的地方.让学生自主学习,就是要让他们恰当地支配自己的时间,让他们成为数学学习的主人,及时地知道自己的长处与不足.就初中数学课堂而言,自主能力具体体现在三个方面.首先,学生要有自主选择训练的能力.换言之,当学生在某一方面有些不足的时候,他们能直面问题,进行相应的强化.比如,有的学生解一元二次方程时答题不规范,老是失分,他们就自主地做一些规范性的训练.以下面这道题为例:4x2-3x+1=0.学生先写出a=4,b=-3,c=1;再写出b2-4ac=(-3)2-4×4×1=-7<0;最后写出原方程无解.明显地,数学学习中要真正地让学生有时间强化自己的弱项.
其次,学生要有自主分析问题的能力.以下面这道题为例:解方程2x2+43x=-22.下面是一个学生的解答过程:a=2,b=43,c=22,所以b2-4ac=(43)2-4×2×22=32.因为x=-b±b2-4ac2a,所以x=-43±3222=-26±4.教师先不点评,让学生自主地分析这道题的对与错.分析就是让学生对每一个过程思考,可以短时间的思考,也可以长时间的思考.让他们在不断地思考中,发现问题的归因.
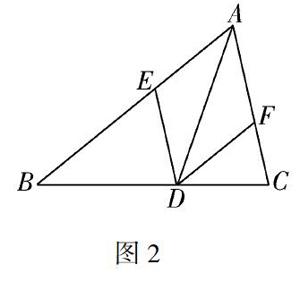
最后学生还要有自主评价的能力.对于初中的数学学习,教师将大多本该属于学生的权利无意中牢牢地握在了自己手上,比如说评价权.学生的表现如何,不是让学生自己去评价,也不是别的学生去评价,教师做得最多的是自己站在讲台上评价,貌似公正,却没有征得学生的同意.其实最好的评价方式就是让学生自主评价,先自己评价自己,再让小组成员相互评价,最后教师再进行点评.明显地,学生自主评价能让学生成为学习的主体,能充分发挥评价的效用,进而使学生的学习能力得到快速图2发展.教师将每次的回答分为1到5分,五个不同的等级,让学生更好地评价自己,也评价别人.以华师大版八年级下菱形的判定为例,有这样一道题:AD平分∠BAC,DE∥AC交AB于点E,DF∥AB交AC于点F,求证:四边形AEDF是菱形.一名学生根据文字的叙述画出了图2,另一名学生举手说出了自己的看法:该同学能准确地将文字里蘊含的信息在图形中表现出来,很不错,其实能画图,基本就能解答了.同时,他还指出这名同学在画AD平分∠BAC时没有按照角平分线的画法去操作,比较随意.这是来自学生的评价,这样的评价更贴近学生的真实情况,他们容易接受,也容易改正.又有一名学生说,对照图形,此题由已知条件DE∥AC,DF∥AB,可以发现四边形AEDF是平行四边形,那么由平行四边形得菱形需要添加什么条件呢?这个学生问教师,他这样的表现能得几分,问的问题有没有价值.明显地,学生将评价当成自己的需要,也很看重别人的评价,此时教师可以问他自己的感受.学生说,他能将结论与已知条件对接,一般地,就是要将两者往中间靠拢,以便找到一个连接点,最后证明这个连接点的存在就可以了.因此他认为自己能掌握学习技巧,能得满分.
对于数学学习来说,要让学生有自主的学习习惯,自主选择能让他们抵达自己的最近发展区,能激发他们的兴趣,能让他们将数学学习当成一次主动建构.自主分析能让学生的思维得到充分的锻炼,能让他们发挥思维的长处去弥补自己的短处.自主分析,强调对学生思维的引发,强调学生潜力的挖掘.自我评价更好地展示学生的自我能效,让他们在认清别人的同时也发现更好的自己.
三、积累智慧,培养学生的合作能力
当前的初中数学课堂也出现了许多合作的模式,最常见的就是小组合作与师徒结对.合作的目的旨在让学生充分汲取别人的智慧,让素养走上提升的快车道.但大多数的合作都存在两个方面的问题,一方面是教师强迫学生去合作,学生本身对合作不感兴趣.学生不感兴趣的原因大致有三个方面:首先,合作中的假讨论,本来就会的问题,还在不间断地讨论,没有提升的可能;其次,合作中的不和谐,教师在分组的时候没有做过细的工作,没能将性格互补、思维互补的学生放在一起,即要让学生在彼此身上都看到闪光点,不能出现彼此嫌弃,彼此拆台的现象;最后,讨论的问题超越了大部分学生的认知,学生无从下手开展合作,只是等教师从旁边经过的时候说一些表面与主题有关,实则不痛不痒的话语.另一个方面是合作受时空限制,大多数学生离开了课堂就放弃了合作.因而从某种意义上来说,合作变成了逢场作戏.其实在任何时候,只要一个组的学生有两个人在一起的时候就可以合作.合作能培养学生听取别人的观点,修正自己的不足;合作也能让学生看到自己的不足,进而让自己多了一份要强的心.更重要的是,合作能让学生更好地展示自己,能让他们多元的能力得到锻炼.
教师在培养学生合作能力时,首先要让学生自由地分组,让他们选择和自己喜欢的人坐在一起,让他们对合作充满兴趣.但为了组与组的均等,教师在征得学生同意的情况下要做一些调整.其次,教师要让学生展示真正的合作片段.以下面这道题为例:关于x的方程m+1xm2+2+m-2x-1=0,让学生学着提出问题.这个题目看上去就有点难,这时可以采用小组合作.学生先将想到的问题写出来,想不出问题的,再与别人讨论.有学生想到这样的问题:假如该方程为一元一次方程,m是否存在.这个学生想出来的问题,就激发了别的学生的思路.于是就有这样的问题:假如m存在的话,能不能求出m并解此方程.又有学生抢着说:假如该方程为一元二次方程,m是否存在.这是一次真正地合作,学生都真正地思考,同时每个人都想展示自己的价值.
图3最后,合作要有领头羊.以六个人的小组为例,合作过程中有三个组长,两个人为一个小组,一个师父,一个徒弟,师父要带着徒弟去学,让合作能做到有目的,有秩序,进而能有所生长.领头羊的作用,就是这个师父能随时关注这个徒弟,不管是在学习上还是生活上都能起一个监督作用.还以菱形的判定为例,已知E为菱形ABCD边BC上一点,AB=AE,AE交BD于点O,且∠DAE=2∠BAE,求证:EB=OA.有些学生看到这样的题目就懵掉了,因为这是一道稍微有点复杂的几何综合题.解决这类题时,师父可以告诉徒弟要先审清题意,将题目中的已知条件在图形上作适当的标注.师父问:如看到E为菱形ABCD边BC上一点这个已知条件时,会想到什么?徒弟只要懂点相关的常识就可以联想菱形边的性质,即四边相等,对边平行,即AD∥BC,AD=BC.师父再问:由AB=AE又能得到什么?徒弟回答:根据等边对等角,得∠ABE=∠AEB.到这儿,学生几乎放弃时,小组的三个师父一商量,进而发现要证EB=OA,这两条线段分别位于两个三角形当中,一般会怎么做.有了师父的引领,合作深化了,学生的思考也深化了.最后三个师父里选一个代表作有关合作的总结.学生说,通过此题大家要能够体会到几何题一般的解题思路,由已知想可知,由未知想需知,联想已学的知识,打通已知与未知的桥梁.
结束语 质疑、自主、合作是素养培育下初中数学课堂必须要走的三步棋,它让学生的成长有了具体的方式与方向.同时,这三步棋又在彼此的作用下,让学生的能力尽情地展示出来,进而在数学的大棋盘上做到招招制胜.
【参考文献】
[1]王章永,杨贵宾.初中数学课堂教学中渗透核心素养的几条途径[J].数学大世界(上旬),2017(2).
[2]黄玉华.基于初中数学核心素养的教学实践与思考:以苏科版七年级下“§12.2证明(1)”为例[J].中学数学杂志,2016(12).

