基于建构主义的逆矩阵教学设计与实践

詹环 陈平 夏静

摘  要：针对逆矩阵教学中重计算、轻思想的问题，结合建构主义教学理念，在教学中分析学生已有的知识结构，从逆矩阵的几何背景的角度引入定义，注重逆矩阵与其相关知识点的联结，利用数学软件开展教学拓展，培养学生抽象思维能力和解决实际问题的能力。

关键词：建构主义;逆矩阵;教学设计

中图分类号：G642       文献标志码：A         文章编号：2096-000X（2020）27-0119-03

Abstract： In order to solve problems of emphasizing calculation and neglecting thought appearing in reverse matrix teaching， construtivism theory was utilized toanalyze cognitive structure of students， inverse matrix was introduced from the point of view geometric， the connection between the inverse matrix and its related knowledge was focused， mathematics software was used to expand teaching tocultivate the students' ability of abstract thinking and the practical problems-solving.

Keywords： constructivism; reverse matrix; teaching design

线性代数是工科各专业的必修课，它主要研究有限维线性空间及其线性映射的理论课程，广泛应用于自然科学和工程技术工作领域中，具有较强的抽象性和逻辑性[1]。矩阵的逆是矩阵的一种基本运算，它是解线性方程组、矩阵方程的基本工具，也是研究线性逆变换、坐标逆变换以及矩阵相似变换的基本手段。由于有些教师在讲逆矩阵知识点的过程中，偏重于逆矩阵判定条件以及计算涉及的公式技巧，对于逆矩阵产生背景、蕴含的逆变换思想方法直接舍弃或者一句带过，导致学生只是对逆矩阵的定义及计算死记硬背，缺乏对逆矩阵的几何意义的认识，很难将逆矩阵灵活应用于解决实际问题。

建构主义理论是由瑞士心理学家皮亚杰提出的，建构主义认为学习不是一个被动的接受过程， 而是一个主动的建构过程，不能从教师通過“刺激反应”迁移到学生，而必须基于学生对知识的体察，从自身经验的反省，与环境，包括与他人的交流中主动地建构起来[2]。建构主义要求教学以学生为中心，根据学生已有的认知结构精心设计教学情景，激发学生的学习兴趣，达到使学生建构知识的目的。本文从图形的几何变换引入逆矩阵的定义，让学生明白学习逆矩阵的缘由，随后在逆矩阵习题设置中强调了逆矩阵和逆变换的意义，通过经济学中的实例对逆矩阵教学进行拓展，使学生掌握利用矩阵的逆进行逆变换的思想，最后借助思维导图帮助学生建构系统的知识体系，符合学生的认知规律。

一、学情分析

建构主义要求教师根据学生已有的知识水平创设符合教学内容要求的情境，设计问题引起学生的思考和讨论，使得学生有意识地对习得的知识进行建构，所以教师必须了解学生已有的知识和所学的专业，避免教学内容前后脱节。教学中应尽量选取贴近学生生活的实例为教学内容做铺垫，线性代数是以线性方程组与矩阵为主线的学科，学生已经掌握了矩阵的加法、减法、乘法运算以及相应的矩阵变换，学生自然会产生疑问矩阵有没有除法？矩阵乘法的逆运算应如何定义？

二、创设情境，引入定义

教师如果完全按照教材先给出一个抽象的线性变换，然后写出对应的矩阵方程再求逆变换，这种不直观的引入逆矩阵的教学方式容易让学生感觉到迷惑。随着计算机科学技术的发展，计算机图形学的应用领域越来越广，图形的几何变换，包括图形的平移、旋转、放缩等，是计算机图形学中经常遇到的问题[3]。一个平面的图形在计算机上存储为顶点的集合，通过画出顶点，并将顶点用直线相连即可得到图形。用矩阵表示图形的顶点的集合，则平面图形的平移、旋转、放缩都可用矩阵乘法实现，以图形的旋转变换为例引入逆矩阵的定义。

例1设一个图像A由11个点连接填充构成，它的位置用一个2×11矩阵表示，顶点的横坐标储存在矩阵的第一行，纵坐标储存在矩阵的第二行，A从X的位置逆时针旋转90°得到Y，其中

Y=0 -14 -14  0 0 -11 -6 -6 -4.5 -4.5 00  4   6  10 8  5  3.5 6.1 6.5  3.2  2，问图像原来位于何处？

解：将点P（x，y）逆时针旋转？渍得到P1（x1，y1），则旋转变换为x1=xcos？渍-ysin？渍y1=xsin？渍+ycos？渍令R=cos？渍 -sin？渍sin？渍cos？渍，则点的旋转变换可以用矩阵乘积Rxy=x1y1表示，则图像A逆时针旋转90°可表示为Y=0 -11  0X，已知Y求X。

求解图形旋转变换的原图问题就转化为解矩阵方程RX=Y，学生容易根据已有的知识联想到借助解一元线性方程y=ax的思路来解决这个实际问题。对于y=ax，当a≠0时，可解出x=a-1y。对于矩阵也存在类似的运算，自然想到是否可以把RX=Y中的旋转变换矩阵R移到等式另外一边，得到旋转逆变换，即X=R-1Y。由此引入逆矩阵的概念。

定义1[4]对于n阶矩阵A，如果存在n阶矩阵B，使得AB=BA=E，则称矩阵A是可逆的，并称B为A的逆矩阵，简称逆阵。

根据逆矩阵定义，当矩阵可逆时，由旋转变换等式RX=Y容易得到图像复原等式X=R-1Y。利用实例引入逆矩阵的定义强调了逆变换思想的形成过程，与建构主义的教学理念一致，重视了数学概念的来源，揭示了逆矩阵的本质。

三、数形结合，阐述定理

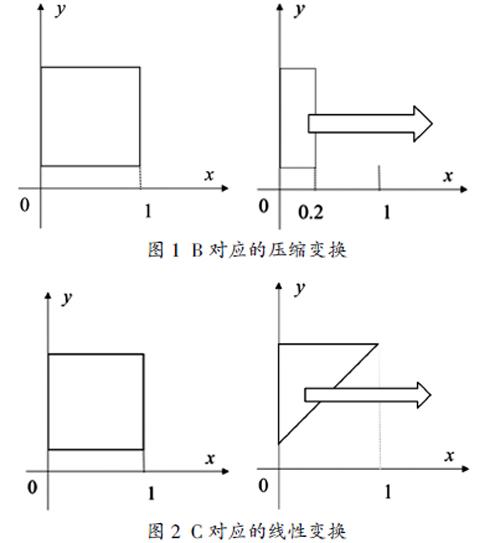
建构主义认为，为了让学生了解知识产生的来龙去脉，积极地参与到知识形成的过程中去，要求教师根据教学内容特点合理设置问题协助学生完成对新知识的意义建构。从心理学角度出发，人对图表的记忆力会比单纯的文字强很多，图形能更好的表达数学概念和定理的意义，在逆矩阵教学中可以设置可视化例题。

显然，只需要将压缩的图像的横坐标拉伸5倍即可恢复图像，即该压缩变换有逆变换。学生容易找到

矩阵C=1 00 0代表图像变换x1y1=1 00 0xy，即x1=xy1=0，从几何图形上可知该变换不可逆，由矩阵定义也可以验证C=1 00 0无逆矩阵。

根据例2可知不是所有的矩阵都可逆，由此引入逆矩阵的判定条件。

定理1[4]若矩阵A可逆，则|A|≠0。

由例2矩阵B行列式不为零，矩阵B可逆;矩阵C行列式为零，矩阵C不可逆，这进一步验证了定理1的正确性。数学家华罗庚曾说过：“数缺形时少直觉，形少数时难入微。数形结合百般好，割裂分家万事非。”将逆矩阵教学应用于实例，并将知识点尽量可视化可以提高教学效果。

四、结合数学软件，思维拓展

美国在1990年提出了线性代数改革的建议中要求线性代数教学要从具体例子引出概念和理论，计算机技术必须要应用到线性代数教学中[5]。逆矩阵与图像处理有着密切的联系，借助matlab求解得到原图像所对应矩阵

建构主义要求教师在教学中不仅要体现主导作用，更要发挥学生的主观能动性。组织学生们进行协作性学习，使得学生在探究性学习中发现规律，纠正和补充对所学内容的认识。在研究多个经济部门之间的投入与产出关系时， W. Leontief教授提出了投入产出模型，我们将下面的“投入产出问题”作为习题， 要求学生独立思考，完成解答。

练习[3]：某地有一座煤矿， 一个发电厂和一条铁路， 经成本核算， 每生产价值1元钱的煤需消耗0.3元的电; 为了把这1元钱的煤运出去需花费0.2元的运费; 每生产1元的电需0.6元的煤作燃料; 为了运行电厂的辅助设备需消耗本身0.1元的电， 还需要花费0.1元的运费; 作为铁路局， 每提供1元运费的运输需消耗0.5元的煤， 辅助设备要消耗0.1元的电. 现煤矿接到外地6万元煤的订货， 电厂有10万元电的外地需求， 问： 煤矿和电厂各生产多少才能满足需求？

五、构建思维导图，梳理知识体系

逆矩阵的定义以及计算是线性代数中的重要知识点，通过逆矩阵的学习，学生能够容易记住判定逆矩阵的条件以及逆矩阵计算公式，但是学生容易“只见树木，不见森林”。建構主义认为认知结构是将已认识的知识组织起来的心理系统，借助于树型特别是网状结构将相互联系的知识点按照某种关系进行归类和组合，可以对认知结构进行“扩容”，提高学习效率[6]。思维导图可以将细碎的知识以简单的形式有组织有次序的表达出来，为了让学生清晰掌握逆矩阵的地位作用，结合思维导图来帮助学生理解逆矩阵与线性代数中知识点的联系，避免让逆矩阵教学内容与其它内容脱节，逆矩阵思维导图见图3。

六、结束语

在逆矩阵教学中，不仅仅要求学生掌握基本的计算，更重要的是培养学生数学思维的方法，提高学生的工程实践能力。在工科背景下建构主义教学理念的指导下，结合实例把逆变换的几何背景引入到各个知识点中，把抽象问题形象化，使学生在形和数的统一中进一步体会到逆矩阵概念的内涵和外延，利用数学软件结合经济案例进行探究性学习，借助思维导图帮助学生建立一个系统、交叉的知识体系。真正建立价值塑造、能力培养、知识传授三位一体的教育模式有效提高教学质量。

参考文献：

[1]张肇炽，徐仲.代数与几何基础[M].北京：高等教育出版社，2003：7-36.

[2]何克抗.建构主义——革新传统教学的理论基础[M].北京：北京师范大学出版社，1999：26.

[3]陈怀琛，高淑萍，杨威.工程线性代数[M].北京：电子工业出版社，2007：157-158.

[4]同济大学数学系.工程数学线性代数[M].北京：高等教育出版社，2014：42-50.

[5]陈怀琛.实用大众线性代数[M].西安：西安电子科技大学出版社，2019：1-2.

[6]王龙.建构主义教学观与文科高数教学[J].黑龙江高教，2008（8）：163-165.