露天深孔空气间隔装药爆破的数值模拟研究

张晓平, 马建军, 刘 令

(1.武汉科技大学理学院， 武汉 430065； 2.中铁广州工程局-武汉科技大学爆破技术研究中心， 武汉 430081)

露天大直径深孔爆破由于孔网参数较大，往往会产生较多的大块，而增大了二次处理大块的工作量，因此在大直径条件下如何控制岩石的爆破块度是目前工程中急需解决的问题[1]。

中外学者就通过改变装药结构来改善爆破效果、控制爆破块度进行了长期、大量的研究。早在20世纪40年代，Melniokov等[2-3]认为可以采用间隔装药的形式来减少一次爆破时的装药量，降低爆压峰值。赵继忠[4]进行露天台阶爆破时得出，应用空气间隔装药技术的爆破效果与传统连续装药相比，大块率明显减少、炸药单耗降低。陈寿如等[5]在相似材料模型中和相同试验条件下，通过测试连续装药和空气间隔装药的应力波波形对比，定性地说明了采用空气间隔装药，可以增加用于破碎或抛掷岩石的爆炸能量，提高了能量利用率。近年来，学者们针对空气间隔在孔内设置的位置、长度(占炮孔长度比例)等方面开展了大量研究。明悦等[6]在露天爆破中通过改变不同空气间隔装药位置来进行现场爆破对比试验，发现当空气间隔层置于炮孔中部时，岩石的破碎块度效果最好。李瑶等[7]对不同空气层位置和比例的空气间隔装药进行了混凝土模型爆破试验，结果表明在相同空气间隔比例条件下，中部空气间隔较下部或上部间隔对岩石爆破块度的影响更大。高鹏飞等[8]为了改善露天爆破大块率高等问题，应用ANSYS/LS-DYNA 有限元软件，在装药不变条件下进行空气间隔比例分别为 10%、12.5%、15%、17.5%和 20%的中部空气间隔的模拟计算，结果表明空气层比例为炮孔长度的 17.5%时，岩石爆破破碎的块度分布最均匀。

虽然前人在应用空气间隔装药控制岩石的爆破块度方面取得了大量研究成果，但其研究均以上下两部分装药为总装药的1/2来考虑的。实际上，现场露天台阶爆破下部抵抗线较大、岩石夹制作用大往往装药较多，上部少一些，而上下两部分各占总药量多大比为好，却没有定论。而关于上下装药比例不同，采用不同空气间隔长度对爆破效果的影响尚鲜见报道。为此，拟通过理论分析空气间隔装药作用原理，运用ANSYS/LS-DYNA有限元软件模拟不同装药比例下，空气间隔长度的变化对岩石的爆破破碎效果影响，得出最佳的空气间隔装药结构方式，为现场实际爆破提供理论参考。

1 空气间隔装药破岩作用的力学模型

空气间隔装药包括将空气间隔设置在顶部、中部和下部三种形式[8]，选择应用最普遍的中部间隔来探讨。这样空气间隔将岩石爆破区域分为A′、B′、C′三部分，如图1(a)所示。对于A′区，上部装药爆破部分，炸药爆炸所产生的爆轰波直接作用于炮孔壁，使孔壁产生破坏，爆轰波进入岩石随即衰减为冲击波P1在岩石内部传播。当其传播到岩石表面，即自由面时，反射为拉伸波P11。同时A′区岩石也受到下部装药爆炸向上传播的冲击波P2的作用，因此A′区岩石是在压缩波P1、拉伸波P11和压缩波P2的共同作用下产生破坏和生成裂缝的。B′区岩石为空气柱作用区间，其孔壁受上部下向传播冲击波P1和下部向上传播冲击波P2的作用，当P1、P2相遇，两冲击波产生叠加，使冲击波压力达到最大，在孔壁上产生最大合压力P′，使B′区岩石产生破坏和生成裂缝。C区岩石受下部炸药爆炸产生的向上冲击波P2及上部炸药向下传播的冲击波P1的共同作用，而产生破坏。

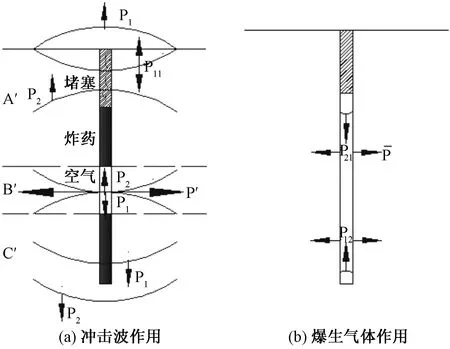
图1 冲击波与爆生气体在炮孔内部作用Fig.1 Shock waves and explosive gases acting inside the blasthole

由于炸药爆炸瞬间完成，因此可认为炸药爆炸后在炮孔内只有爆生气体，以及原有的间隔空气柱。当上部炸药爆炸产生冲击波P1、下部炸药爆炸产生的冲击波P2，它们一方面直接压缩空气柱，另一方面作用于岩壁和堵塞物时，由于岩石和堵塞的波阻抗远大于空气的波阻抗，而在交界面上反射为增强了的压缩波P21和P12，对途经岩石进行再次作用，进一步加深扩展裂纹，对岩石造成“二次作用”。同时在冲击波P1、P2，反射压缩波P12、P21和爆生气体压力的共同作用下，空气柱气体被不断压缩，而形成一个新的“空气高压源”向四周施压。其作用于孔壁，对已形成的裂隙和微裂缝进行楔入、延展和贯通破碎，达到自由面将岩石抛出，图1(b)所示。

与连续装药相比，中部空气间隔装药一方面将炸药在孔内两段分布，以空气柱相隔，降低了爆压峰值，减小了岩石的过度粉碎；另一方面冲击波多次在孔内作用，延长了爆压作用时间，使岩石获得更大的爆破冲量，爆炸能沿炮孔分布更为均匀，从而提高了能量利用率。同时，冲击波在孔壁的多次作用，使炮孔四周产生更多的裂纹或原有裂纹得到更好的扩展，从而更有利于岩石的破碎，使岩石破碎块度更为均匀。

2 数值模拟

2.1 计算模型

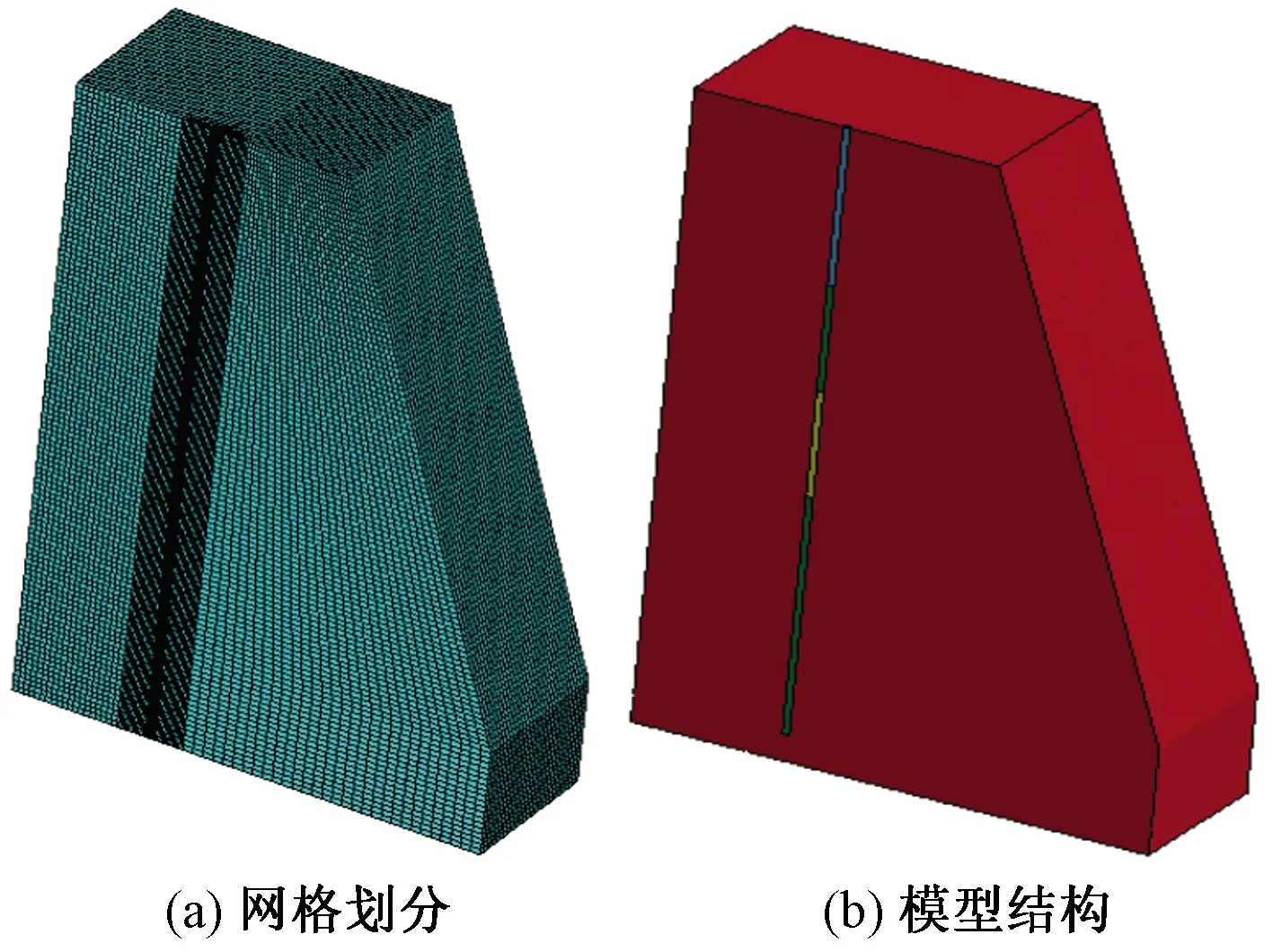
图2 网格划分与模型结构Fig.2 Model structure and meshing

计算模型包括空气、炸药、岩石及堵塞材料。模拟参数：炮孔直径为120 mm、孔距a=6 m、排距b=5 m、台阶高度10 m、超深1.5 m、孔深11.5 m、装药高度6 m[9-10]；采用中部空气柱间隔装药，上下装药比例为1∶4、3∶7、2∶3及1∶1，对应的空气间隔占比分别为炮孔长度的10%、12.5%、15%、17.5%和20%。为此建立了20个计算模型，考虑到模型的对称性，为方便计算取1/2模型建模。模型采用3D-SOLID164单元进行网格划分，采用从里往外的方法划分网格，炮孔内单元尺寸为0.01 m，炮孔周围区域0.6 m内单元尺寸为0.04 m，其余单元尺寸均为0.1 m，模型网格划分与模型结构如图2所示。炸药、空气和堵塞材料采用ALE(Aribitrary Layrange-Euler)算法，岩石采用拉格朗日算法，炮孔区域的岩石与炸药、空气和堵塞材料采用流固耦合算法。模型下底面添加固定约束，对称面添加轴向约束，后表面与前表面设定为非反射边界面。

2.2 材料模型

2.2.1 炸药材料模型

根据实际工程，模拟使用2#岩石乳化炸药，在LS-DYNA软件中采用*MAT_HIGH_EXPLOSIVE_BURN高能炸药模型及*JWL状态方程加以描述：

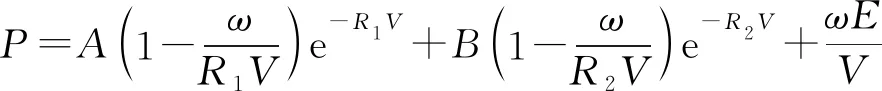
(1)

式(1)中：P为爆轰压力；V为相对体积；E为单位体积内能；ω、A、B、R1、R2为材料常数。具体使用炸药参数如表1所示[11]。

2.2.2 空气材料模型

空气使用*MAT_NULL材料模型及线性多项式状态方程*EOS_LINEAR_POLYNOMIAL加以描述。线性多项式状态方程为

P=C0+C1μ+C2μ2+C3μ3+(C4+C5μ+C6μ2)E

(2)

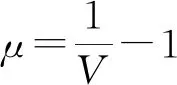
(3)

式中：μ为相对体积简化式；C0～C6为材料常数。具体使用炸药参数如表2所示[12]。

表1 2#岩石乳化炸药参数

表2 空气材料参数

2.2.3 岩石材料模型

岩石采用*MAT_JOHNSON_CONCRETE模型(简称HJC模型)加以描述，该模型考虑了材料的大变形、高应变率及高围压下材料的损伤失效动态响应，能够很好地模拟在爆破荷载作用下岩石的动力学特征，使用的岩石材料参数如表3所示[13-14]。

2.2.4 堵塞材料模型

露天深孔爆破堵塞材料多为砂土材料，使用*MAT_SOIL_AND_FORM材料模型加以描述，模拟具体参数如表4所示[15]。

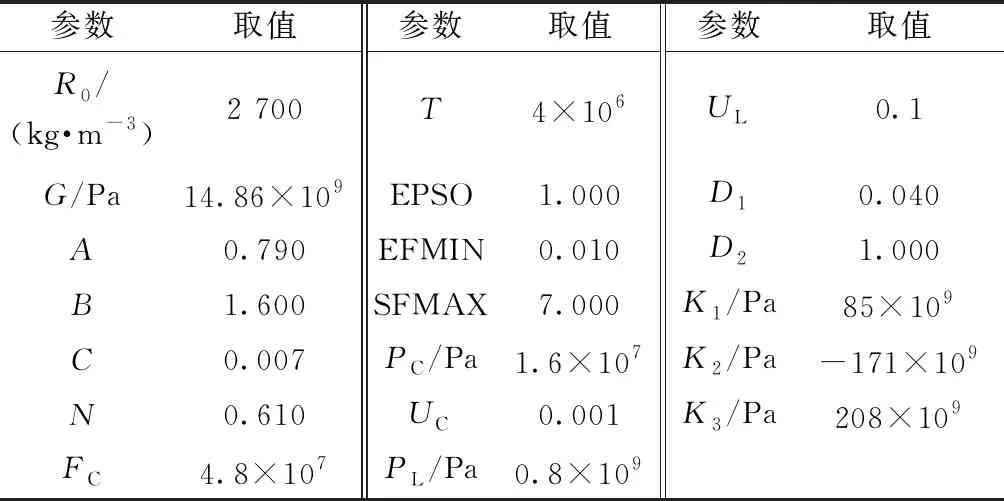
表3 岩石材料参数

表4 堵塞材料参数

2.3 模拟结果分析

对20个计算模型的模拟结果进行分析中，选取空气间隔中间孔壁的受力情况作为研究典型单元，当有效应力大于岩石的强度则岩石破坏。一般岩石的抗拉强度为10～30 MPa[7]，所受平均有效应力值越大，高压作用时间越长，对岩石破坏越有利。各模型计算的典型单元应力峰值及应力均值如表5所示。

2.3.1 连续装药(无空气间隔)炮孔有效应力分析

为了与空气间隔装药爆破效果进行对比，建立连续装药(空气间隔长度为0)模型，选取药柱中间部位孔壁单元进行分析，其有效应力曲线如图3所示。

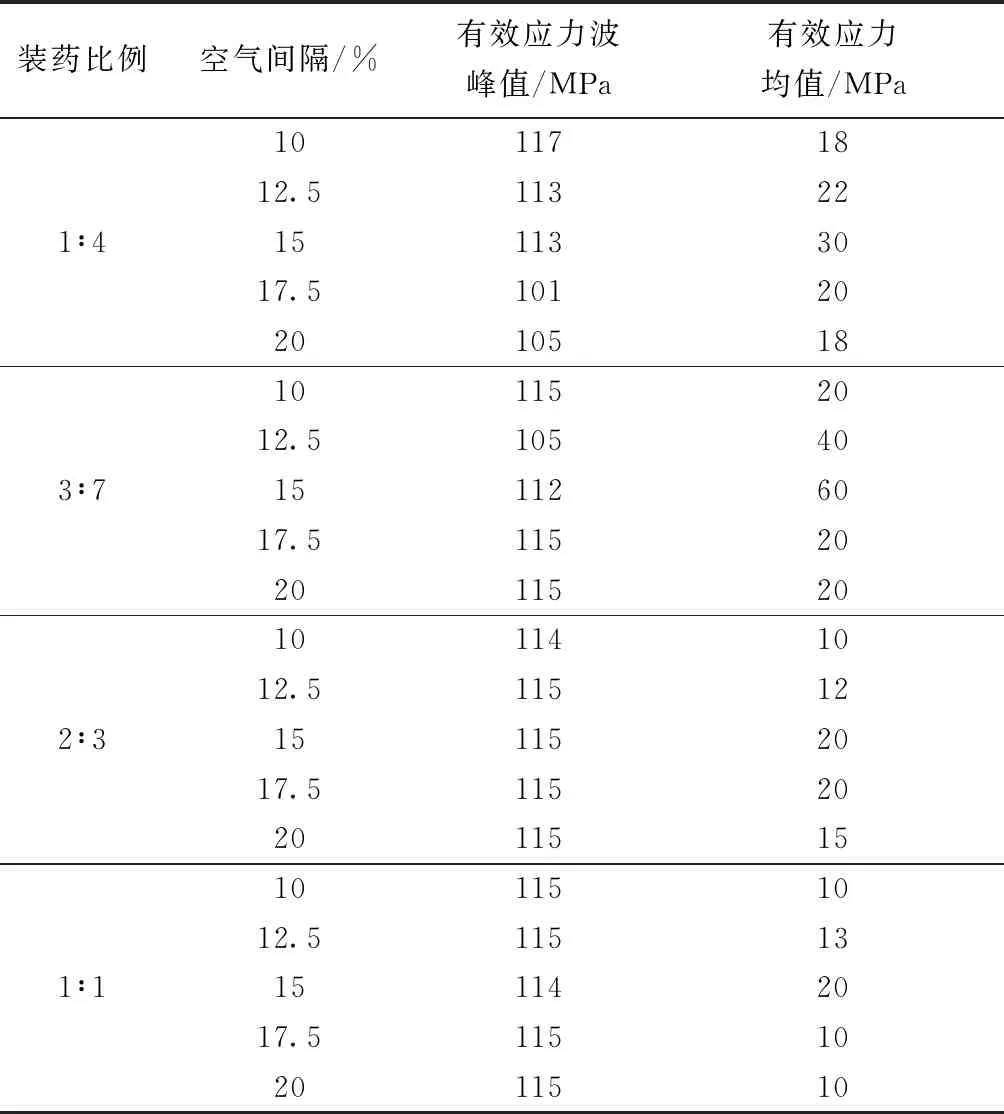
表5 原计算模型应力波压力

由图3可见，采用连续装药，典型单元Au的有效应力曲线，其有效应力峰值为120 MPa，其余大部分时间有效应力在10～30 MPa，平均有效应力相对较低。

2.3.2 空气间隔占比相同炮孔应力波作用分析

空气间隔占比相同，改变上下装药比例，计算典型单元Au的有效应力，并进行有效应力分析。由于篇幅有限，仅列出空气间隔占比为15%时的单元有效应力分布曲线，如图4所示。

由图4可见：空气间隔占比一定、上下装药比例增大时，应力峰值变化不大，但平均有效应力值先增后减；有效应力高的在45～75 MPa，低的在10～50 MPa，平均有效应力和高压作用时间明显大于连续装药；且当上下装药比例为3∶7时平均有效应力最高，高压作用时间最长，更有利于岩石破碎。

图3 无空气间隔有效应力变化曲线Fig.3 Curve of effective stress without air gap

图4 空气间隔占比为15%时炮孔有效应力变化曲线Fig.4 Change curve of effective stress of gun bore when the air separation ratio is 15%

利用表5对其余4组数据进行分析，可得出与空气间隔占比为15%时的相似结果。各组有效应力变化曲线如图5所示。

由图5可见，在空气间隔占比一定的条件下，当空气间隔占比为10%～15%时，随上下装药比例的增大，应力波峰值变化不大，但孔内平均有效应力先增后减；当空气间隔占比大于15%时，平均有效应力值相比连续装药其增幅不大，空气间隔聚能作用减弱，甚至消失。因此，为了充分发挥空气间隔的作用，使岩石破碎更为均匀，空气间隔占比为15%。

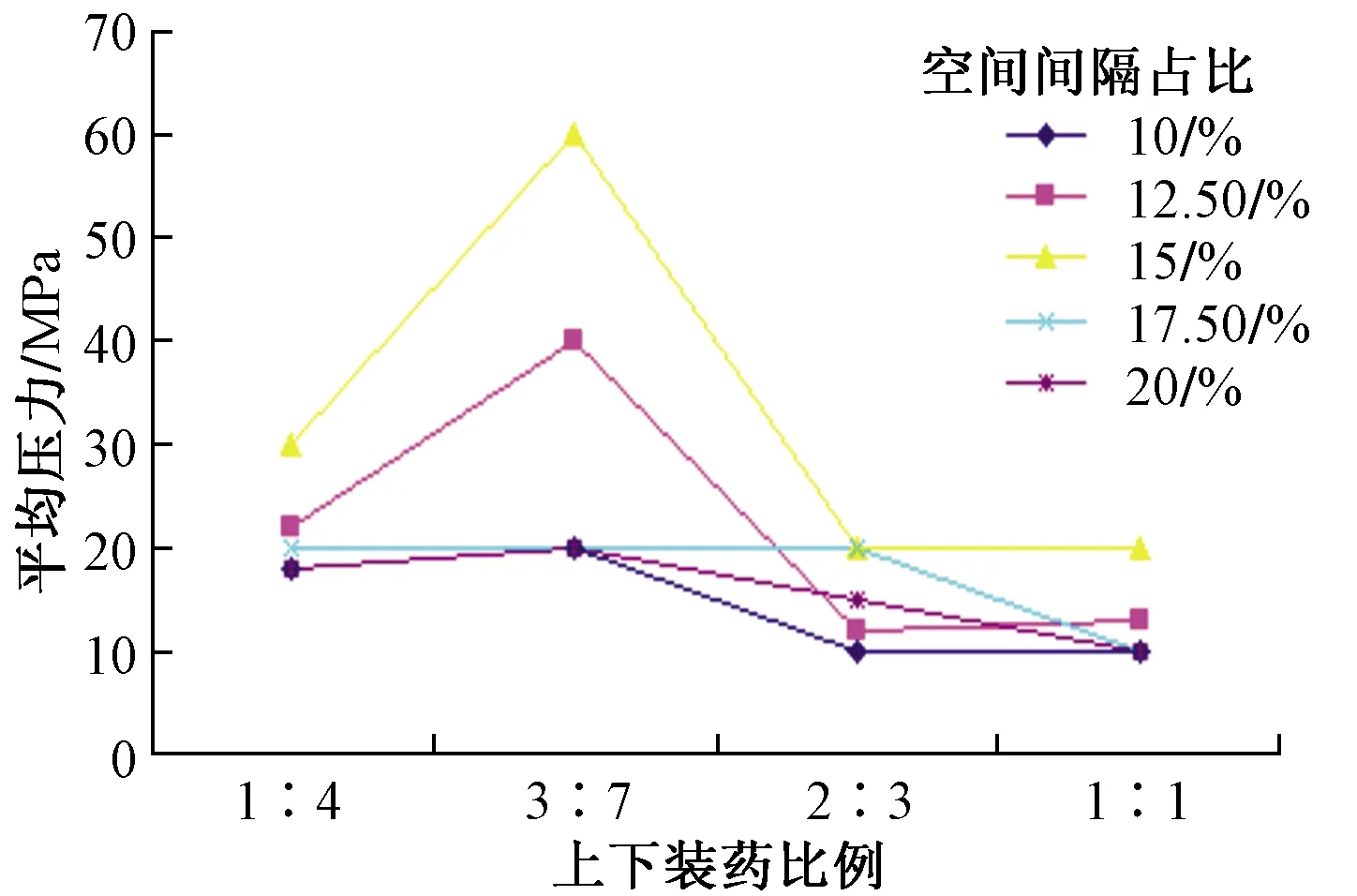
图5 同空气间隔占比下有效应力曲线Fig.5 Effective stress curve under the same air space ratio

2.3.3 上下装药比例相同炮孔应力波作用分析

上下装药比例相同，改变空气间隔占比，计算典型单元有效应力，并进行有效应力分析。由于篇幅有限，仅对上下装药比例为3∶7时的单元有效应力分布曲线，如图6所示。

由图6可见，上下装药比例一定时，随空气间隔占比的增加，有效应力峰值变化不大，但平均有效应力先增后减：有效应力高的在50～80 MPa，低的在15～50 MPa，平均有效应力和高压作用时间明显大于连续装药；且当空气间隔占比为15%时，平均有效应力最大，高压作用时间最长，最有利于岩石的破坏。

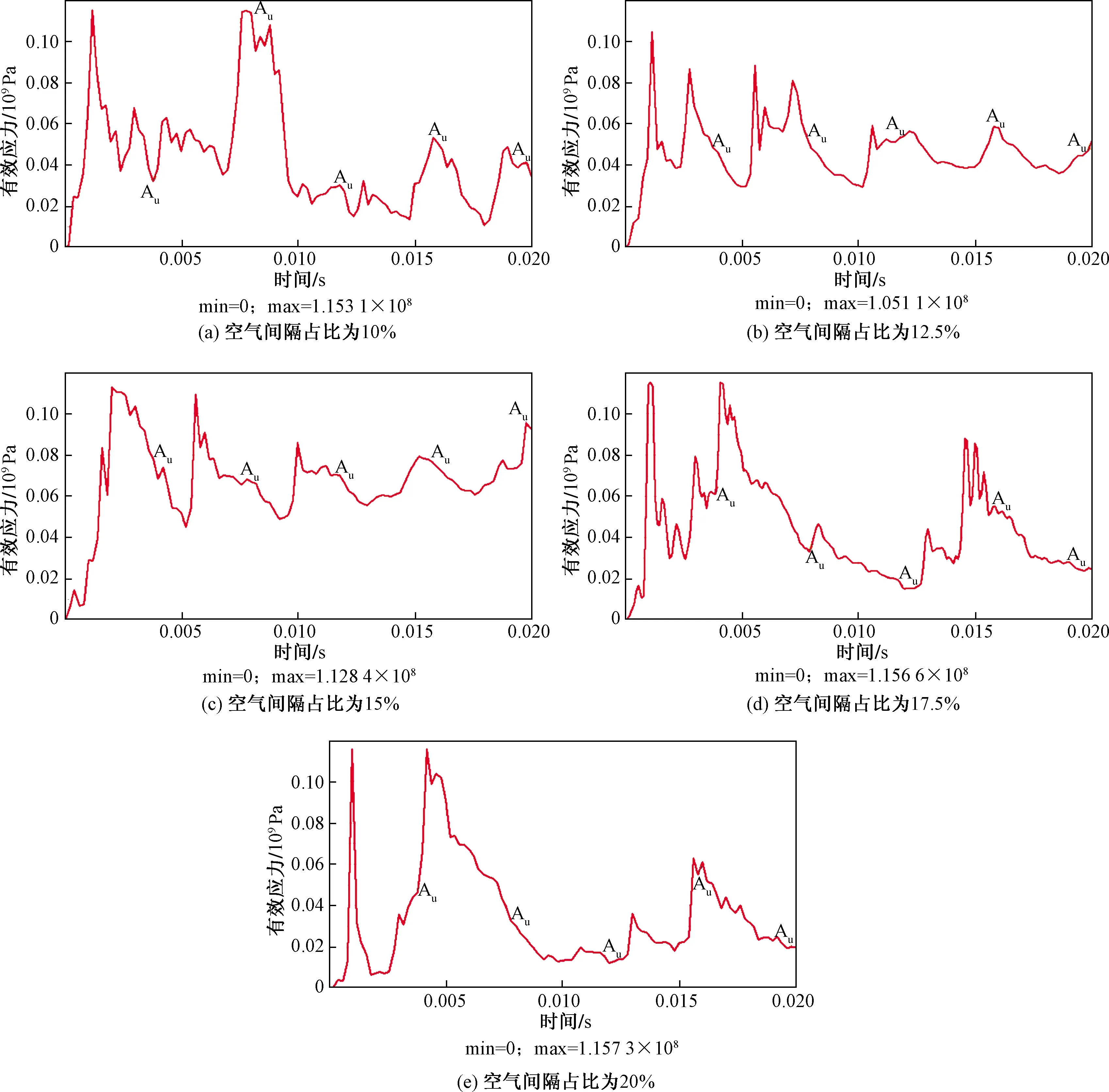
图6 上下装药比例为3∶7时有效应力变化曲线Fig.6 Variation of effective stress when the loading ratio is 3∶7

利用表5对其余3组数据进行分析，可得出与装药比例为3∶7时相似结果，各组有效应力变化如图7所示。

由图7可见，上下装药比例一定时，随着空气间隔占比的增加，孔内平均有效应力先增后减；且当上下装药比例大于3∶7时，孔内平均有效应力与连续装药相比增幅不大，空气间隔聚能作用效果减弱，甚至消失。因此，为了充分发挥空气间隔的聚能作用，使岩石破碎更为均匀，上下装药比例应以不大于3∶7为宜。

2.3.4 空气间隔装药爆破沿炮孔长度的应力分析

选取空气间隔中间水平截面进行应力分析，为了解不同空气间隔装药爆破沿炮孔长度的应力分布，截取了各模型垂直截面的应力云图进行分析。由于篇幅有限，仅列出上下装药比例为3∶7、空气间隔占比为15%的4个典型时刻应力云图，如图8所示。

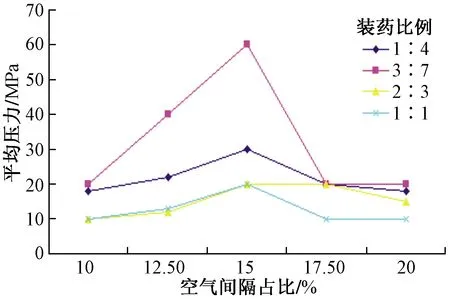
图7 同上下装药比例下有效应力曲线Fig.7 Effective stress curve under the same proportion of upper and lower charges

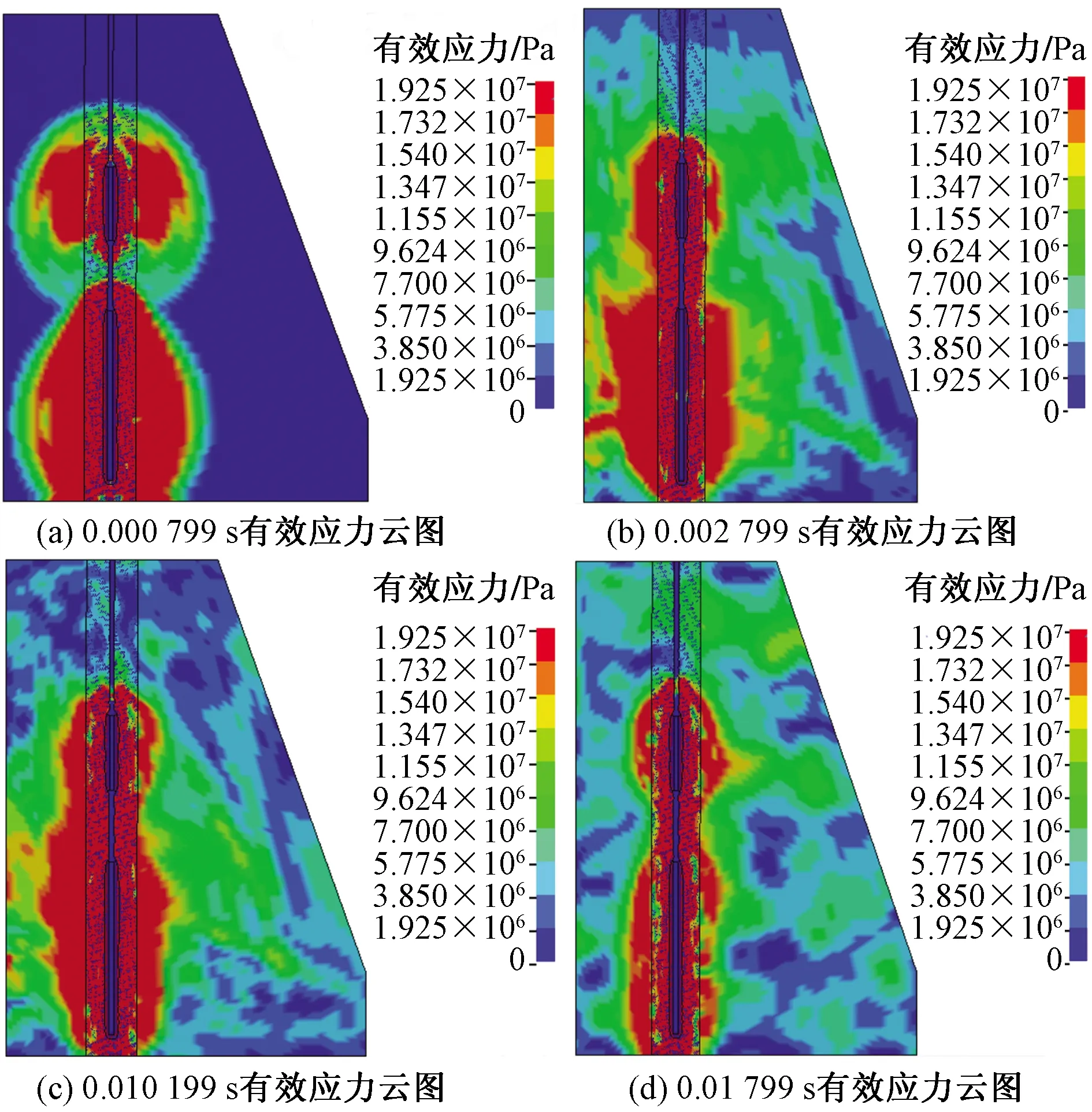
图8 装药比例为3∶7空气间隔为15%有效应力云图Fig.8 Effective stress cloud diagram with charge ratio of 3∶7 and air interval of 15%

由图8可见，炸药爆炸初期上下两药包炸点出现高压应力波，并沿空气柱相向发展、汇聚，使空气间隔段形成与装药段一样的高压应力，直至爆炸结束。同时与其他各装药结构的应力云图进行对比，得出当上下装药比例为3∶7、空气间隔占比为15%时，炮孔周围应力分布相对更均匀、分布面积更广、高压作用时间更长，因此更有利于岩石的破碎和块度分布均匀。

3 模拟结果的一般性验证

为验证上述结果的可靠性及普适性，采取单孔爆破面积(s=ab=6 m×5 m=30 m2)不变，改变炮孔的孔间距(a)、炮孔排间距(b)，即改变炮孔密集度系数(m)，建立上下装药比例为3∶7，不同空气间隔占比的计算模型，进行炮孔密集度系数为1.4、1.6、1.75的空气间隔中间单元的有效应力分析，三组模型对应计算的应力峰值和均值如表6所示。

通过表6数据比较分析可见，单孔爆破面积不变，炮孔密集度系数不同时，当上下装药比例为3∶7、空气间隔占比为15%，孔内平均有效应力最高，高压作用时间最长，相对更有利于岩石的破碎；在模拟计算的三组数据里，随着炮孔密集度系数的增大，孔内平均有效应力减小，破岩作用减弱，因此为使岩石爆破作用强、破碎块度均匀，炮孔密集度系数不宜过大。

4 结论

(1)当空气间隔占比一定，随上下装药比例的增加，炮孔内部平均有效应力先增后减：当上下装药比例大于一定值时，孔内平均应力增幅减小，高压作用时间减小，空气间隔的聚能破岩作用减弱。

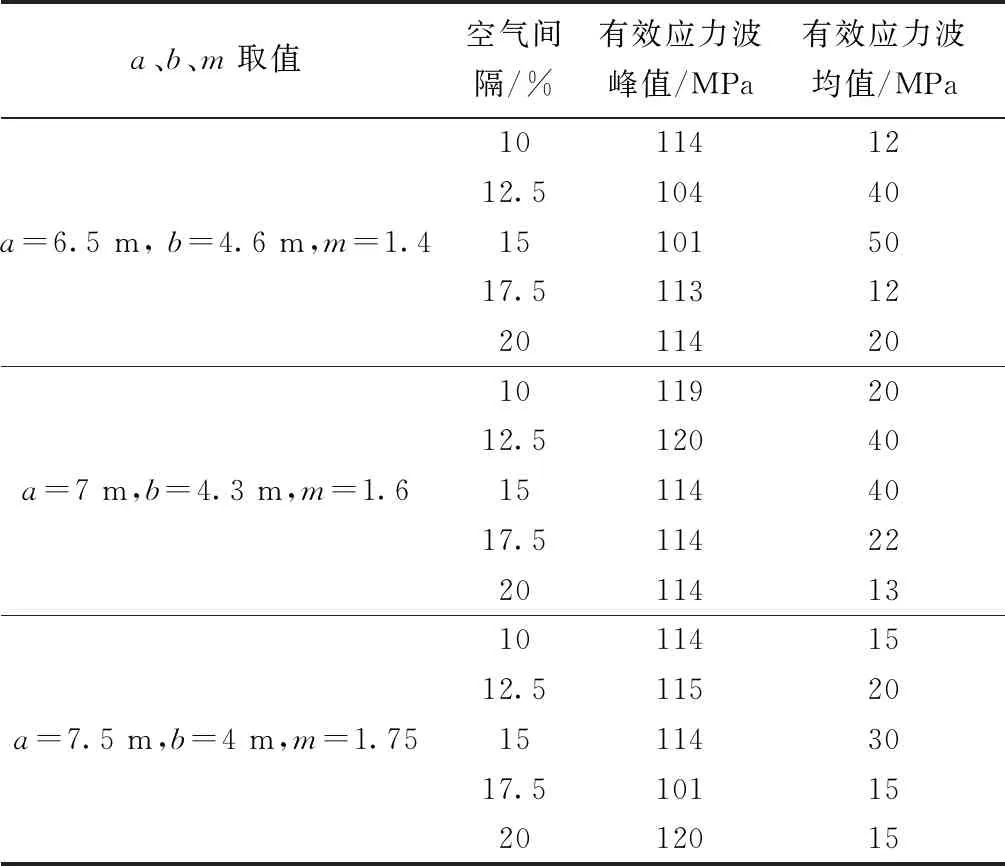
表6 孔距排距变化计算模型

(2)当上下装药比例一定，随空气间隔占比的增加，孔内平均有效应力先增大后减小：当空气间隔占比大于一定值时，孔内平均应力增幅减小，高压作用时间减小，空气间隔聚能破岩作用减弱。

(3)采用空气间隔装药爆破，选取上下装药比例为3∶7、空气间隔占比为15%时，平均有效应力相对较高，孔内高压作用时间相对较长，有效能量利用率更高，更有利于岩石的破碎。

(4)采用空气间隔装药爆破，炮孔密集度系数不宜过大。