覆冰舞动下500 kV猫头铁塔损伤分析及改造技术

陈 彬， 梁 旭， 詹东博， 石青松， 李勃铖， 张 楠

(1.三峡大学湖北省输电线路工程技术研究中心， 宜昌 443002； 2.三峡大学电气与新能源学院， 宜昌 443002)

近年来，导地线覆冰舞动已成为中国超高压输电线路猫头塔倒塌的重要起因之一[1-3]。猫头塔因其导线水平间距小、使用钢材少等特点而广泛应用于高压输电线路，但该塔型在覆冰舞动条件下塔材受力较设计时存在较大差异，塔的薄弱点区域也发生了明显改变，致使布置在输电塔薄弱点上的应变检测装置的预警功能无法实现[4]。鉴于此，准确定位500 kV猫头塔在覆冰舞动下的薄弱点区域对于预防猫头塔倒塌事故和针对性补强具有重要的现实应用意义[5-7]。

实验分析法是获取输电塔薄弱点区域最有效、最直接的途径，但由于输电塔形式多样、气象条件复杂，无法采用实验分析法来研究不同输电塔薄弱点区域的分布规律。对于猫头塔的薄弱点区域主要是依靠各段塔材的应力比值来确定的。而应力比值是通过内力来获取的，当前对于塔材内力的计算方法主要有数值法和解析法[8]。文献[9]在ANSYS中建立2塔3线的输电铁塔塔-线体系，使用一致模态法研究了覆冰断线情况下的内力模拟，结果与实际较为吻合，但没有考虑塔材连接方式和塔材方向问题。文献[10]基于考虑连接螺栓滑移的输电铁塔塔-线体系模型，采用虚拟材料法研究了风载荷条件下的位移响应，但模型将绝缘子串和4分裂导线分别简化为刚性杆件和单导线，由此带来的误差无法预估。在后续的解析法研究中，文献[11]在计算输电铁塔受力中引进了该算法，求解了220 kV干字塔的塔头内力，但并未提出方法验证；文献[12]分别运用解析法和有限元法对薄壁箱形横向温度应力进行求解，结果表明解析法与有限元法吻合很好，前者简便灵活，更适于工程应用；文献[13]考虑了在覆冰舞动下导线的动态张力对输电铁塔塔材内力的影响程度。截至当前，解析法仍然是一种较为精确并且常用的铁塔塔材受力计算方法，但上述文献中所应用的模型过于简化，没有考虑到输电铁塔为超静定结构，从而造成了输电铁塔内力值与实际值仍有较大误差。

针对上述问题，首先根据覆冰舞动条件下的气象参数得到铁塔受力情况，引入力法的概念，对塔中所有的二力杆件进行简化去除，将具有超静定结构的全塔进行分解，构建全塔1/4的模型，对超静定反力进行求解，进而得到全塔杆件的受力情况，并与仿真内力对比分析；对较危险区域的连接螺栓进行受力分析，对超出安全阈值的螺栓进行补强，对比分析补强前后螺栓连接的受力情况。在补强方案经过验证后，基于螺栓的最大预紧力求解了螺母预紧时的旋转角度。

1 猫头塔薄弱点定位及改造方案

1.1 铁塔内力计算方法

在力学理论中，在几何静定体系中施加一个及以上的多余约束而形成的几何不变结构即为超静定结构。将铁塔作为静定结构考虑时，应用节点法或截面法对猫头塔内力由上而下地计算，得到的经典薄弱点大多位于塔头与塔身连接点区域。而将全塔作为超静定结构来求解时，一般采用力法或位移法来进行求解。位移法适用于一次超静定结构的求解，求解速度快且计算简便，而猫头塔的桁架结构多为超静定次数不小于2次的超静定结构。力法适用于超静定次数大于1的结构体系的力学计算，但应用力法解题中，系数和自由项的求解极为繁琐。文献[14]通过超静定次数n确定n个不同的静定结构，使得系数和自由项的求解过程大大简化，进而求解出每个基本结构的未知力，利用n个基本结构叠加得到最后的总未知力，这样力法方程的实用性也就大大提高了。

选取力法来对具有n次超静定结构猫头塔的杆件内力进行求解，首先需要确定该结构的超静定次数，针对性地解除其多余约束，将猫头塔塔头和塔身在连接点处分解成两部分，再将塔头在上下曲臂连接点处分解，引入n次超静定结构的力法方程在连接点处施加单位约束力[14]，结合基本静定结构和变形协调条件从上而下依次求解各塔材内力，进而确定覆冰舞动条件下的薄弱点区域。

1.2 薄弱点处连接螺栓分析及补强方案

铁塔塔材之间的内力传递都是靠螺栓组来实现的，螺纹连接因其结构简单、装配方便、连接可靠等优点而成为输电铁塔塔材之间最常用的连接方式。但是螺纹连接失效问题在输电铁塔倒塌和维修记录中所占比例也较大，螺纹连接失效主要表现为螺栓松动、被连接件发生压溃或塑性变形、螺栓断裂等，其中螺栓松动占螺纹失效比例的70%以上[15]。引起螺栓松动的主要原因是初始预紧力不足而造成的螺栓滑移，一旦螺栓滑移程度超过了线弹性挤压阶段(或载荷大于挤压极限应力σm)，螺栓滑移将无法恢复，如图1所示。

在工程实践中，无法直接获得螺栓预紧力，因此，为了预防螺栓松动事故的发生，必须按照机械设计所提供的《紧固件机械性能螺栓、螺钉和螺柱》(GB/T 3098.1—2010)选取拧紧力矩，然后依靠经验公式计算螺栓的预紧力来进行校验，当其不满足要求时，对螺栓进行补强，更换为等厚双帽防松螺栓，再进行校验，直到其满足载荷要求为止。

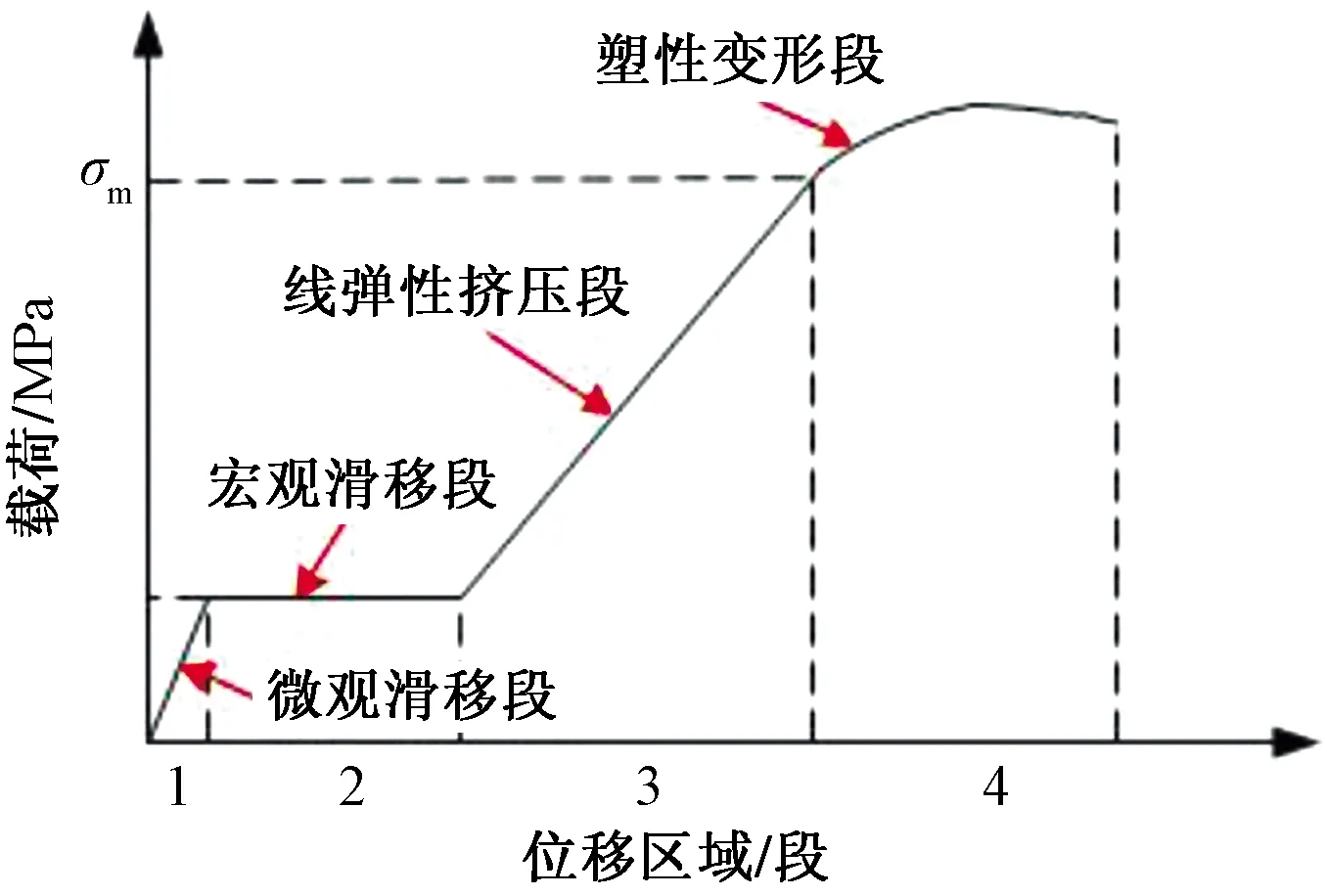
图1 螺栓滑移的载荷-位移关系Fig.1 Load-displacement relationship of bolt slip

1.3 技术路线

对于猫头塔薄弱点区域的准确定位和螺栓补强方案验证的计算流程如图2所示。

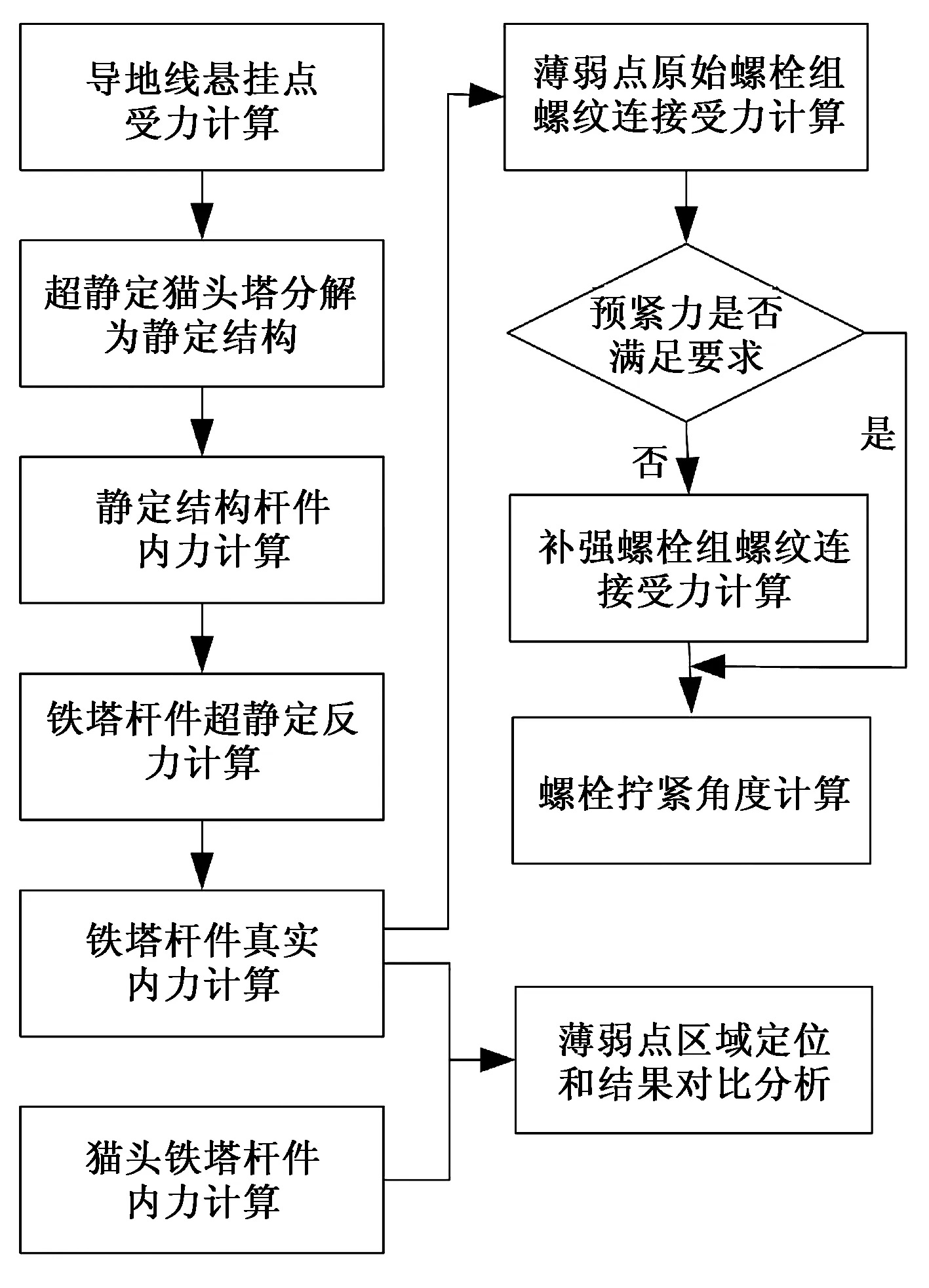
图2 计算流程图Fig.2 Calculation flow chart

2 猫头塔内力及连接螺栓受力计算

2.1 覆冰舞动下的铁塔内力计算

已知导线和地线的规格、导地线设计弧垂最低点应力σ0n、设计温度tn、舞动发生区域的平均气温tm、风速V、覆冰厚度b。如图3所示，按斜抛物线法计算导线最低点应力σ0m的计算公式为[13]

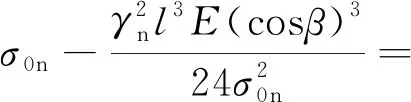
αEcosβ(tn-tm)

(1)

式(1)中：γn、γm分别为导地线无风无冰和覆冰有风

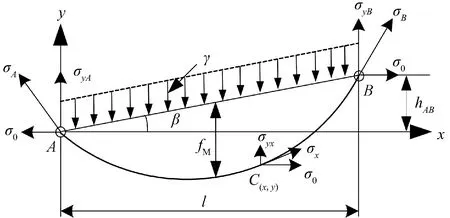
γ为覆冰导地线的综合比载；fM为导地线的弧垂；hAB为A、B两点间的高差；σA、σB分别为导地线上A、B点的应力；σyA、σyB、σyx分别为 A、B、C点的竖直应力；σ0为导地线的水平应力； C(x,y)为导线上任意一点图3 覆冰导线近似为斜抛物线的受力图Fig.3 Force diagram of the ice-covered wire approximated by a diagonal parabola

的单位比载；l为水平档距；E为导地线的综合弹性模量；β为导地线悬挂点高差角；α为导地线的线膨胀系数。

覆冰导地线悬挂点的水平张力(T0)计算公式为

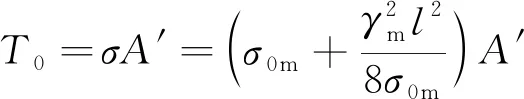
(2)

式(2)中：σ为导地线悬挂点覆冰条件下的静应力；A′为导地线的横截面面积。

此时覆冰导地线的静长度(Ls)计算公式为

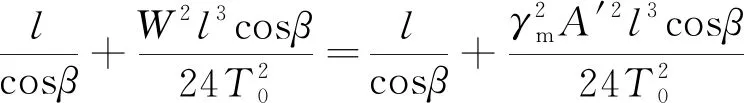
(3)

舞动前覆冰导地线如图4的实线所示，虚线为导地线舞动时的形状轨迹。图4中，TA、TB为导地线悬挂点A、B的轴向张力；TyA、TyB为导地线悬挂点A、B的垂直张力分量；f(x,t)为导地线上横坐标为x的C点在t时刻的舞动动位移；fC(x,t)为导地线上横坐标为x的C点t时刻的静位移；Δf(x,t)为覆冰导地线上C点的位移变化量。

舞动覆冰导地线在t时刻的长度变化量(ΔL)为[13]

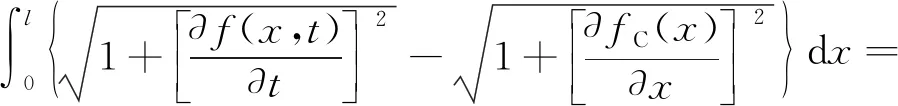
(4)

式(4)中：r为覆冰导地线的舞动半波数；ω为覆冰导地线的舞动角速度；a0为覆冰导地线的舞动幅值。

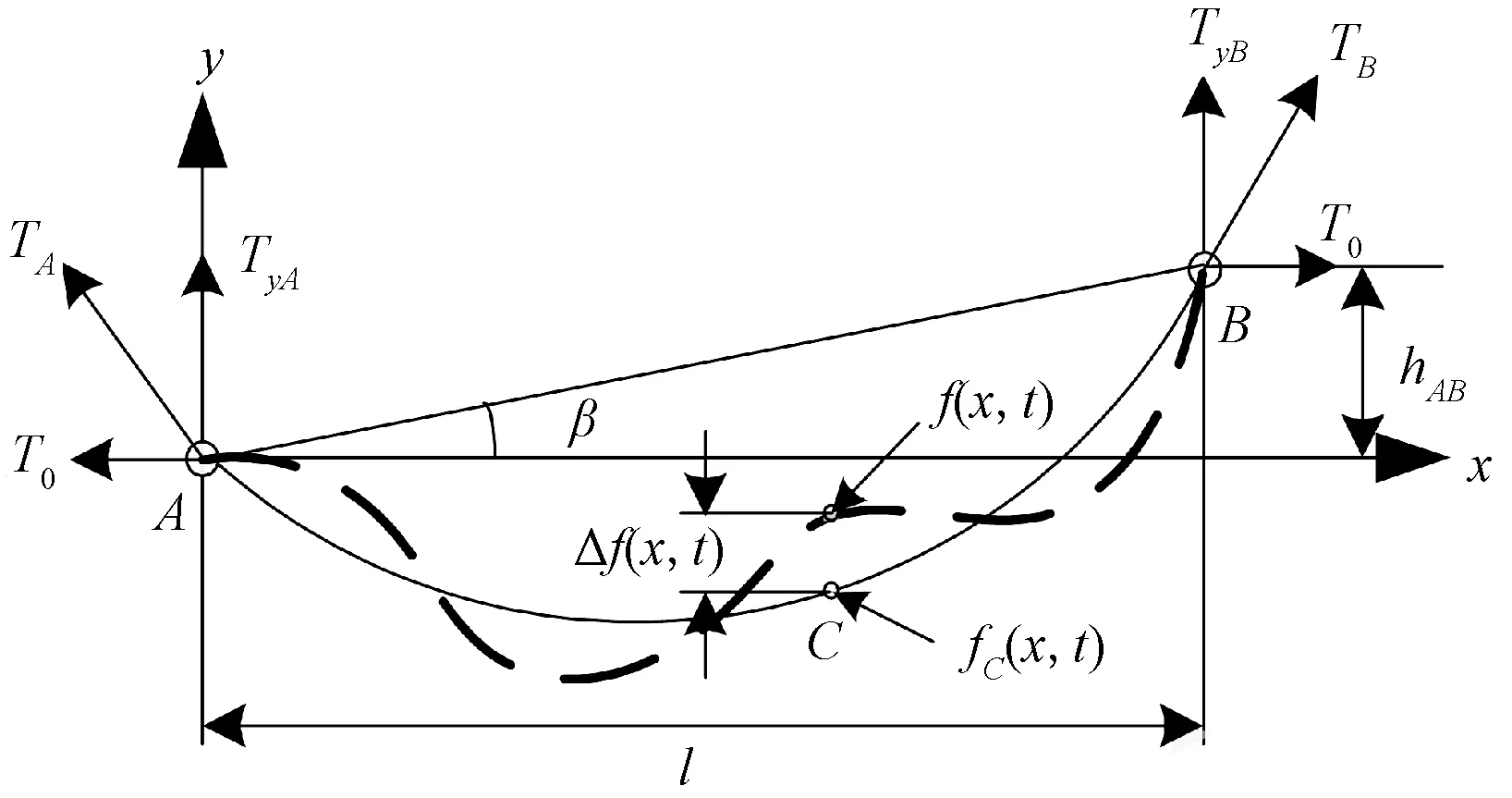
图4 不等高悬挂点导地线形状轨迹Fig.4 Unequal height suspension point guide line shape

由于导地线覆冰舞动是一种低频振动，频率范围在0.1～3 Hz，因此覆冰导地线在一个舞动周期内的弹性变形也是十分缓慢的。将导地线视为一个弹性体来考虑，导地线的受力情况可根据胡克定律来确定，导地线的水平张力变化量计算公式为[13]

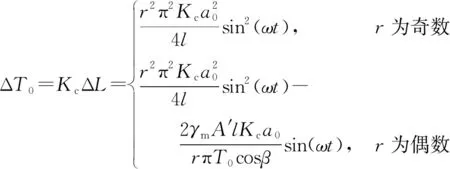
(5)

式(5)中：Kc=EA′/Ls，为覆冰导线综合弹性模量。

舞动发生时，覆冰导线悬挂点的斜率为[8]

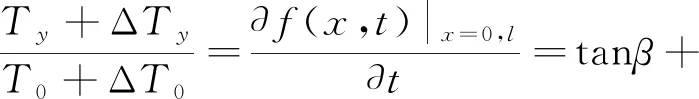
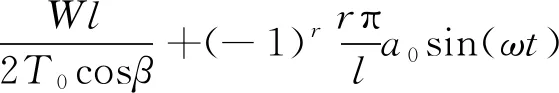
(6)

式(6)中：W=γmA，为覆冰导地线单位长度的荷载。

将式(5)、式(6)结合，正交分析即可求得覆冰导线舞动时悬挂点垂直张力的变化量ΔTy为[13]

ΔTy=

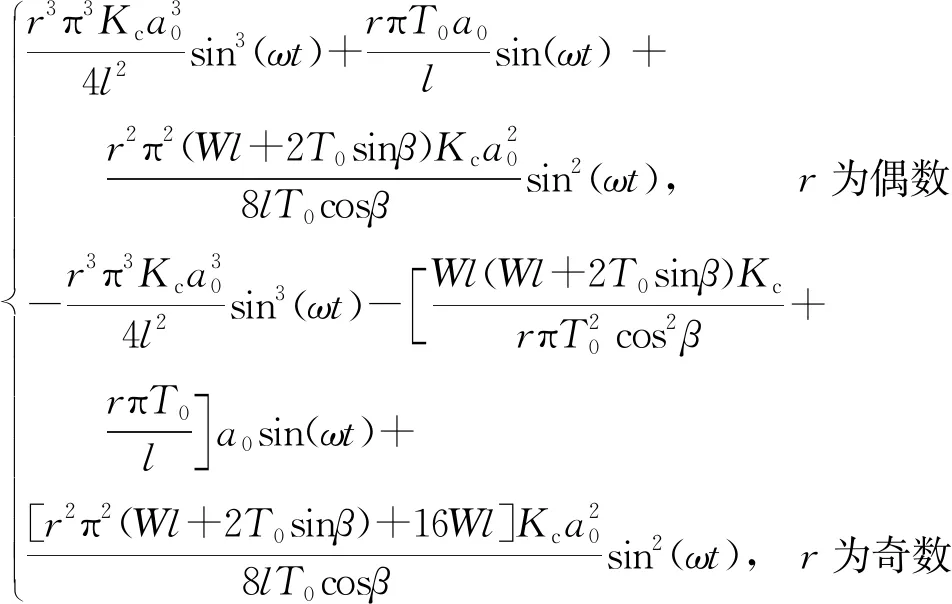
(7)

依据式(1)～式(7)求解的猫头塔在覆冰条件下的受力情况进行塔材内力的计算。首先，由于猫头塔杆件数量巨大，根据以往工程实际和文献参考将猫头塔上的部分二力杆件(辅材和斜材)去掉，合理简化以减小工作量。其次，因猫头塔上的作用荷载均为对称荷载及猫头塔本身为对称结构，只需计算猫头塔的1/4杆件内力即可知道全塔内力，如图5所示。最后，按照力法思想将猫头塔塔身与塔头在连接点处分解，塔头沿着K型节点切开分解为上曲臂和上横担、下曲臂两个部分，这样全塔就变成了基本结构，如图6所示，此时在K型节点处出现反力Rx和Rz。其中Rz可由基本结构的静力平衡条件求得。但Rx必须在垂直荷载和水平荷载作用下分布求解，水平荷载作用下的Rx也可根据基本结构的静力平衡条件求得，而在垂直荷载作用下的Rx自成平衡，故必须由相应K型节点处的相对位移为0来求解。

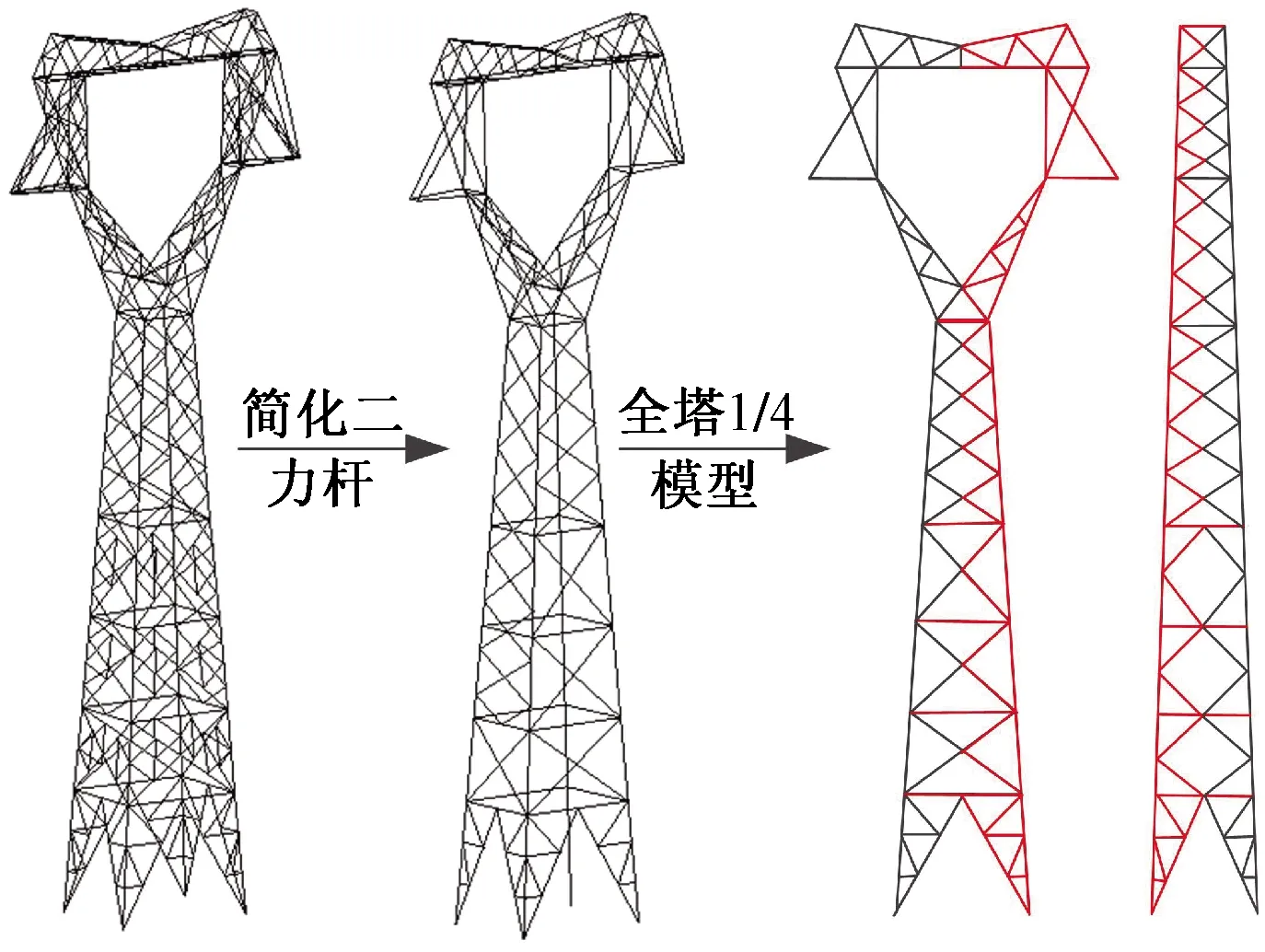
图5 猫头塔简化及分解Fig.5 Simplified and exploded view of cat head tower

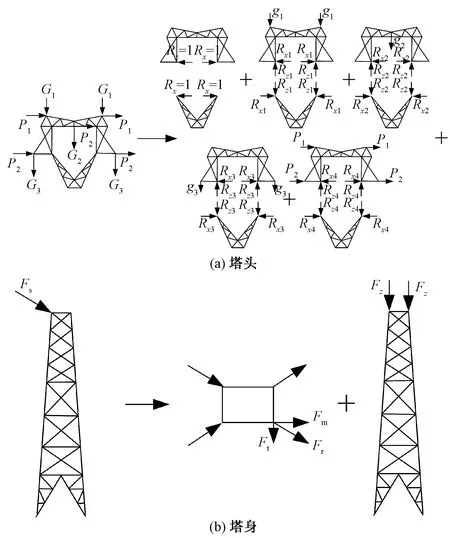
G1、G2、G3分别为地线、中间相导线、边相导线的竖直力；P1、P2分别为地线、导线的水平力；Rx、Rx1、Rx2、Rx3、Rx4分别为仅在无外力、地线单位竖直力、中间相导线单位竖直力、边相导线单位竖直力、导地线单位水平力作用下的水平超静定反力；Rz1、Rz2、Rz3、Rz4分别为仅在无外力、地线单位竖直力、中间相导线单位竖直力、边相导线单位竖直力、导地线单位水平力作用下的竖直超静定反力;Fs为塔头传递給塔身的合力，可分解为竖直力Fz和水平力Fr，其中Fr可沿 方向进一步分解为切向力Ft和周向力Fm图6 猫头塔杆件受力分解Fig.6 Cat head tower force exploded view

在相应接口处建立n次超静定结构的力法方程为[11]

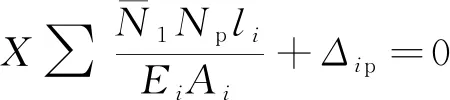
(8)

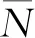
以覆冰舞动荷载下的塔头部分为例进行内力计算，将塔头上所有的水平荷载和垂直荷载作用下塔材产生的内力分解为地线重力、中间相导线重力、边相导线重力、水平荷载各自作用下各杆件所产生内力集合，如图6所示。各杆件的内力计算公式为

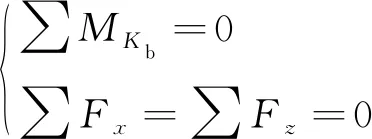
(9)

式(9)中：MKb为各作用力在Kb点产生的力矩；Fx、Fz分别为静定结构水平和垂直方向的作用力。

由上述垂直荷载的各单位荷载产生的超静定反力计算公式为[11]

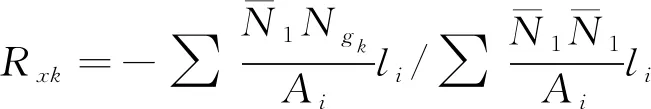
(10)

式(10)中：Ngk为各杆件在导线重力gk=1作用下的单位内力。

覆冰舞动工况下各组合产生的总超静定反力计算公式为

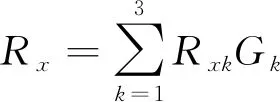
(11)

式(11)中：Gk为覆冰舞动工况下的各垂直荷载的实际值。

任一杆件在垂直荷载及横向荷载作用下的内力可由式(12)求得

(12)

结合式(9)～式(12)即可求得超静定结构的真实内力。

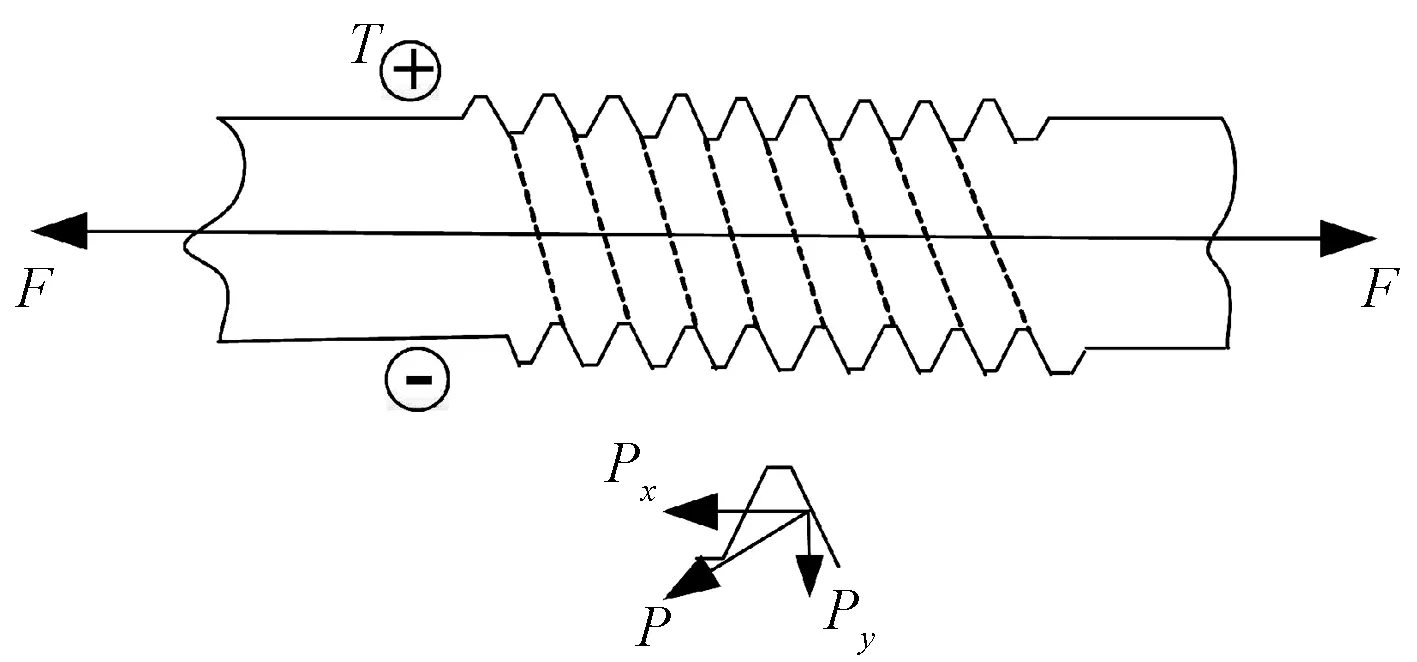
图7 轴力及拧紧力矩作用下的螺纹接头受力模型Fig.7 Force model of threaded joint under axial force and tightening torque

2.2 覆冰舞动下的铁塔连接螺栓计算

螺纹连接通过螺纹啮合实现螺栓杆和螺母的相互连接以达到被连接件紧固的目的[16-19]。在此建立螺纹的二维模型，螺纹牙带有一定的螺纹升角，在螺栓帽上施加一定的轴力和拧紧力矩，螺栓杆外螺纹与螺母内螺纹之间实现接触啮合，啮合过程中由于啮合面上的挤压作用而产生相互作用力。

截取螺纹接头牙体上的一段微元，具体受力模型如图7所示。其受垂直于接触牙体表面的正压力和平行接触牙体表面的摩擦力，它们在单位啮合长度方向上的合力为P，将其分解为水平方向的Px和竖直方向的Py。假定第m牙螺纹的啮合长度为sm，则整个螺纹承担的力F和力矩T分别为[16]

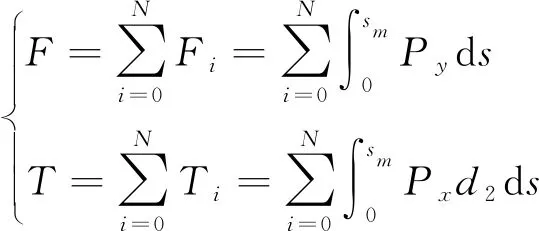
(13)

式(13)中：N为螺纹牙的个数；d2为螺纹牙的中径。

工程螺栓紧固装配都是配备标准扳手施加拧紧力矩来达到量化预紧的目的，预紧时不仅需要克服螺纹副之间的摩擦力矩，还要克服螺栓端面的摩擦作用，因此单个螺栓的预紧力和拧紧力矩之间的转换关系为

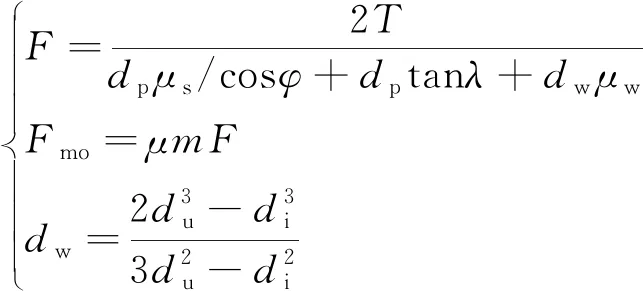
(14)

式(14)中：T为拧紧力矩；dp为有效直径，粗牙螺纹取0.906d2，细牙螺纹取0.918d2；μs、μw、μ分别为螺纹副、螺纹件端面、塔材之间的摩擦系数；φ为螺纹牙角的1/2；λ为螺纹升角，粗牙取2°50′，细牙取2°10′；m为连接螺栓的个数；du、di分别为外螺纹的外径和内径；Fmo为螺栓组的摩擦力；dw为中间计算参数。

要使螺栓不发生松动，需要保证螺栓与螺母之间的连接处于弹性阶段且螺纹副施加的预紧力足够大，即螺栓连接的两块塔材之间的相互摩擦力不小于塔材该点处所受的内力。而工程中仅靠拧紧力矩紧固是无法保证螺纹副的预紧力是否达到要求，在这里引入位移量的概念，将螺纹牙之间看为体弹性接触，基于螺纹体积不变的前提，根据铁塔材料的刚度(K)、体积弹性模量(E)可求得螺纹位移量(S)，进而求得螺纹转角(η)[16]，计算公式为

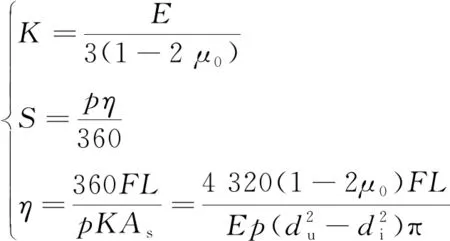
(15)

式(15)中：μ0为泊松比；L为螺纹接触长度；p为螺距；As为中间计算参量。

3 工程实例分析

3.1 荆门工程

以2018年1月份500 kV宜兴Ⅰ回线路在荆门境内76#～208#因覆冰舞动发生倒塌事故为背景，选取141#为例，已知铁塔的模型及参数如图8所示，导地线的规格及基本参数如表1所示线路计算参数如表2所示。

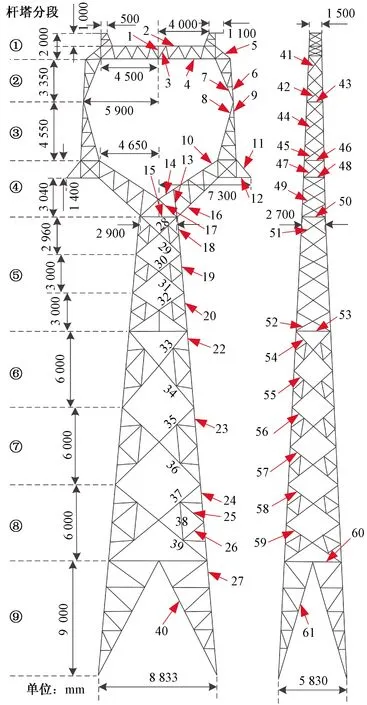
黑色数字表示长度；红色数字表示杆件编号图8 宜兴Ⅰ回线路141#参数及杆件编号Fig.8 Yixing I return line 141# parameters and pole number

表1 导地线型号及规格参数

3.2 超静定铁塔内力计算及分析

根据3.1节中的舞动参数结合式(1)～式(7)可计算出导地线悬挂点处所施加的作用力，计算结果如表3所示，塔身风荷载和塔身本身重量按塔身分段施加，以⑤为例，施加力的作用点如图9所示。

在MATLAB中根据上述的作用力对铁塔杆件采用式(8)～式(12)由上而下进行计算，并在ANSYS中建立全塔模型仿真其内力分布，由于杆件数量较大，在此只列出具有代表性的杆件内力，它们的仿真内力、解析计算内力如图10所示，仿真结果如图11所示。

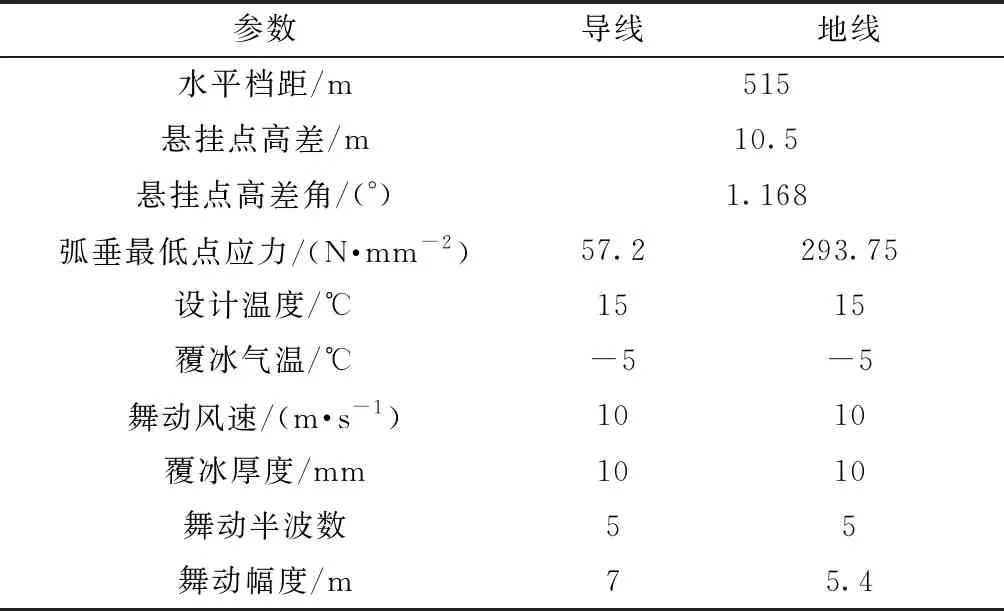
表2 线路计算参数

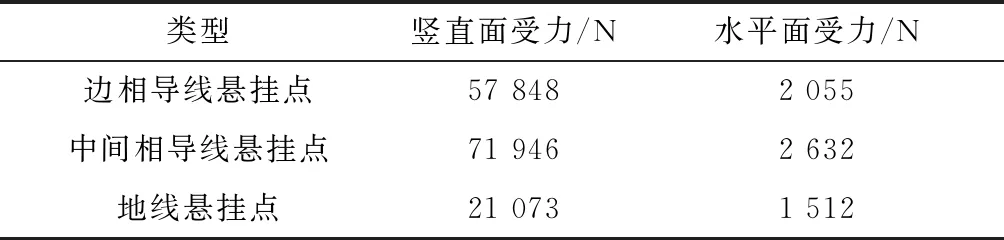
表3 导地线悬挂点的作用力

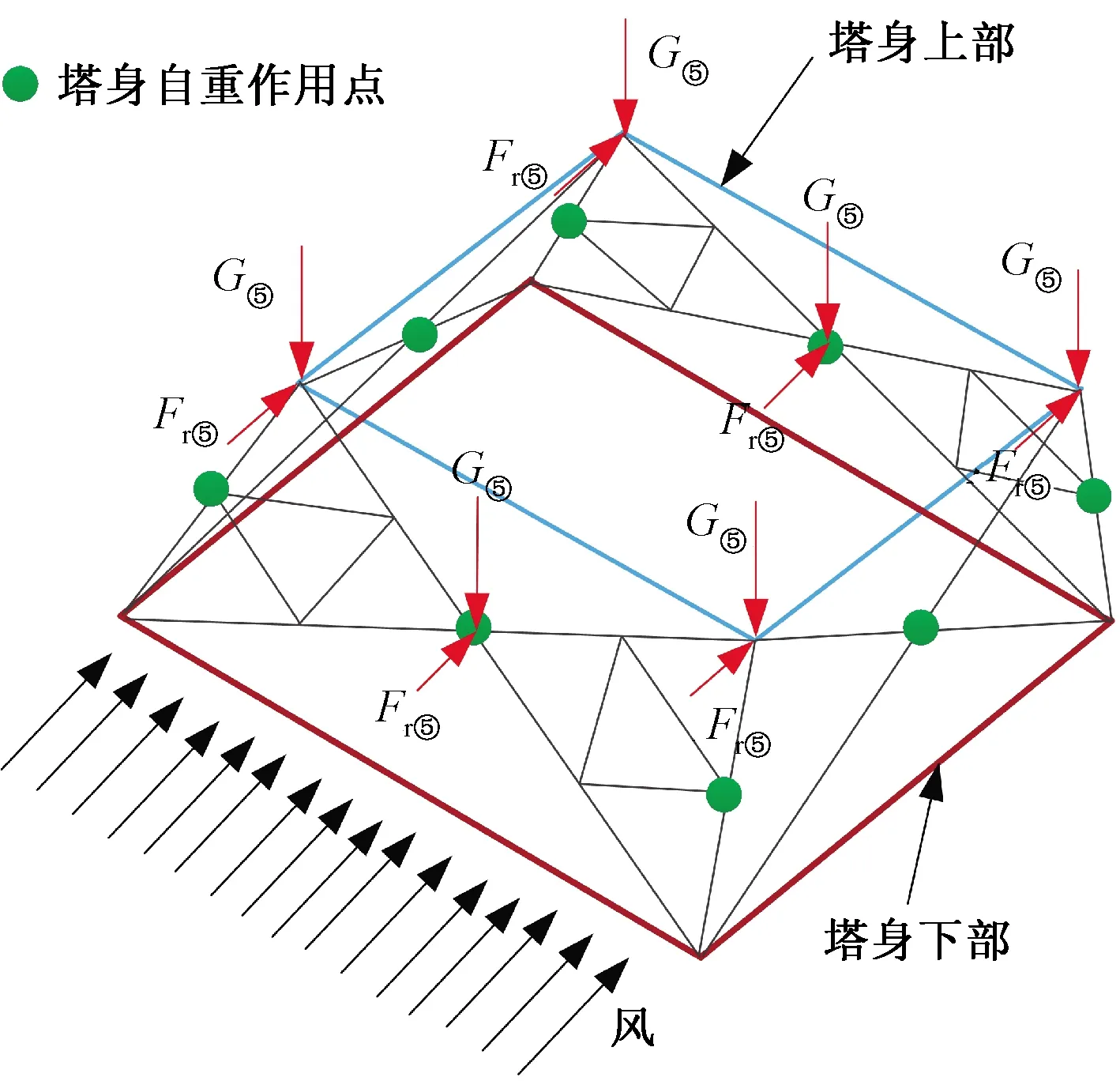
图9 塔身风载和自重作用方式示意图Fig.9 Schematic diagram of the wind load and self-weight mode of the tower body

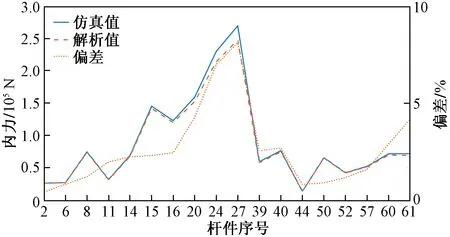
图10 杆件内力值对比Fig.10 Comparison of internal force values of members

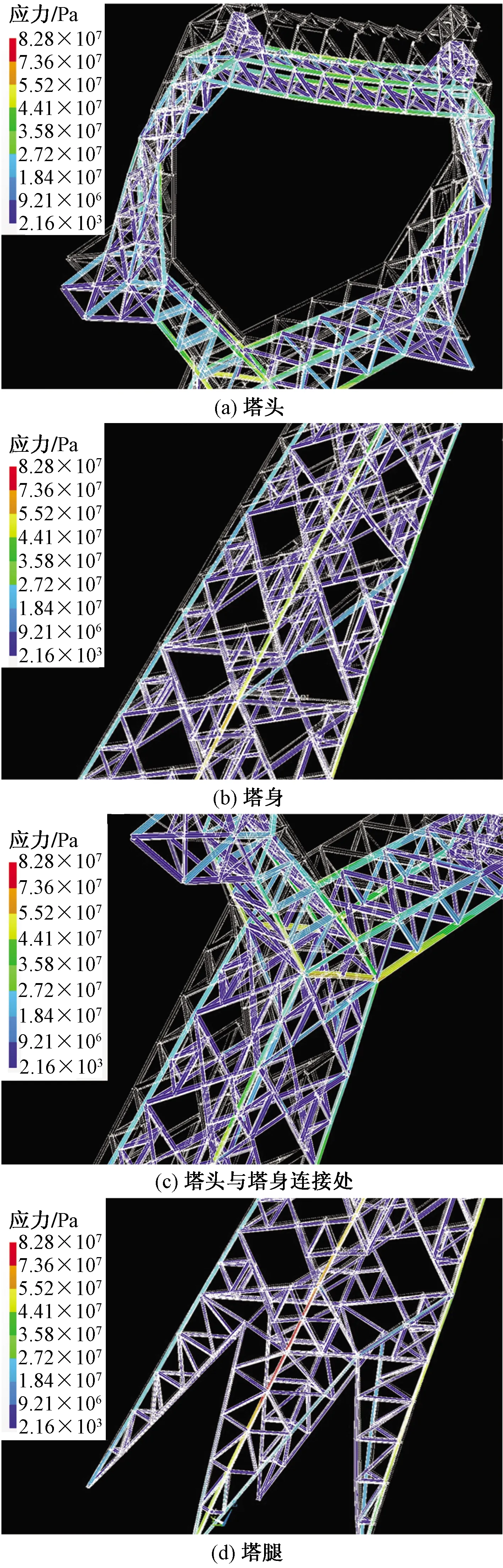
图11 141#应力仿真示意图Fig.11 141# stress simulation diagram

从图8、图10可以看出，覆冰舞动条件下，杆件内力的解析值与仿真值相仿，误差均小于10%，相互印证了计算结果的准确性。塔头与塔身连接处和塔身与塔腿连接处的杆件应力最大，分别为71、83 MPa，塔身主材应力由上至下依次增大，斜材及辅材的应力较小。通过计算杆件所受应力与其许用应力的比值来判断此时杆件的失效情况，计算结果表明：比值的最大值为0.881 1，接近于1，但结构并未发生破坏。因此，铁塔的薄弱区域位于杆件15、24、27。

由图10可知，覆冰舞动条件下，铁塔内力解析值均小于仿真值，主要是因为：①解析计算中塔身风载和自重是按照集中力的方式来施加的，无法做到均匀布置，由此造成的误差无法避免；②几何建模的简化，在仿真研究中，塔材之间均为刚性连接，塔腿与地面之间设置为固定约束等，也对求解结果带来了一定误差；③求解过程中，将连接螺栓和节点板的总重量按节点均布施加，可降低计算难度，但会造成一些误差。

3.3 铁塔连接螺栓校验及补强分析

根据图10中内力计算结果，对各自杆件上的螺栓组的连接强度进行校验。根据式(13)～式(15)计算单个螺纹连接所产生的预紧力，如表4所示，进而计算出整个螺栓组所能提供的摩擦力最大值，将之与杆件的内力相比较，若比值大于1，则此处螺栓组连接可靠，无须补强；反之，则会发生螺栓松动，从而引发铁塔倒塌事故，采取等厚双帽防松螺栓进行补强并校核，螺栓改进示意图如图12所示，校验结果如表5所示。

表4 螺栓型号及其预紧力

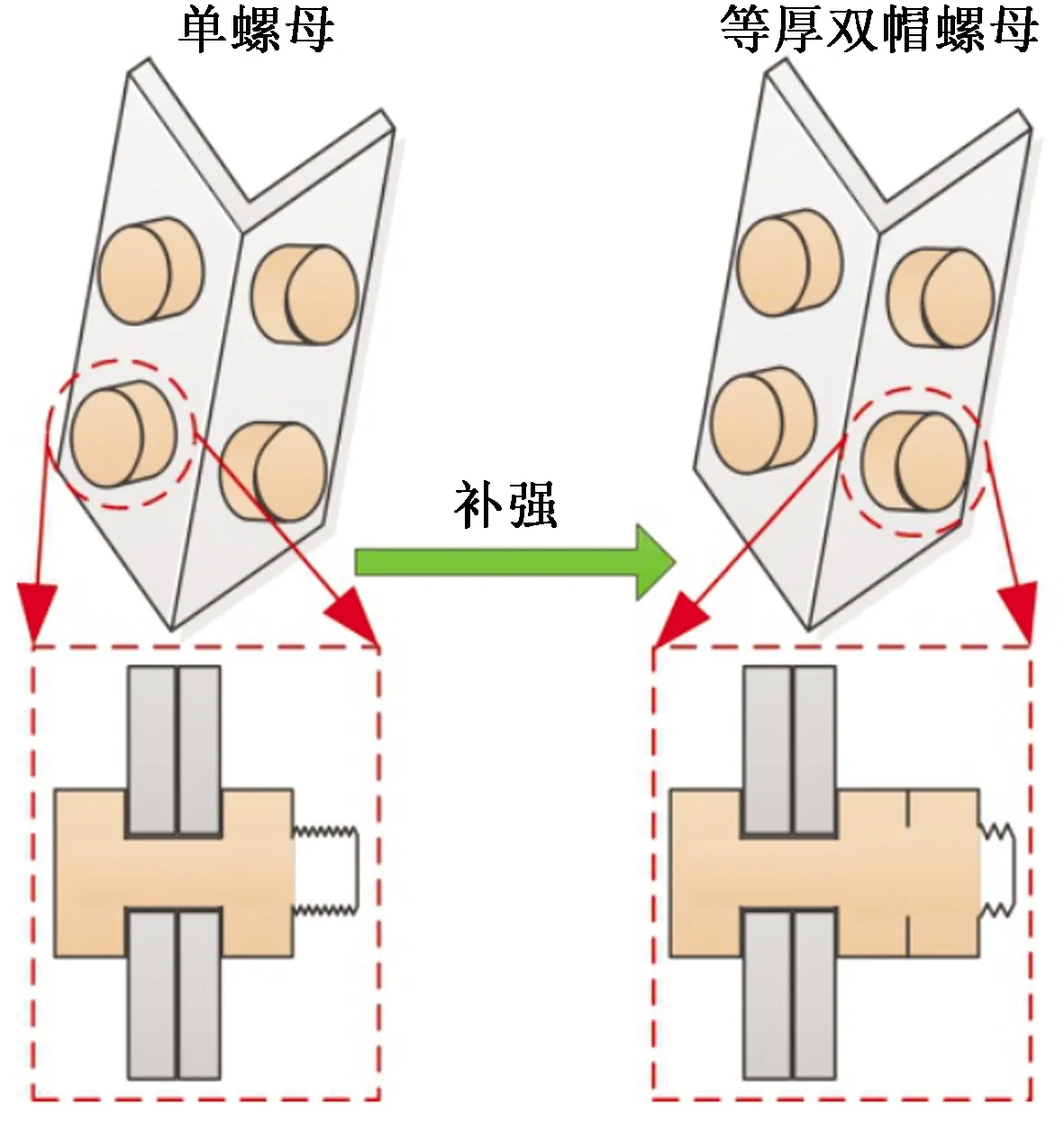
图12 螺栓补强示意图Fig.12 Bolt reinforcement diagram

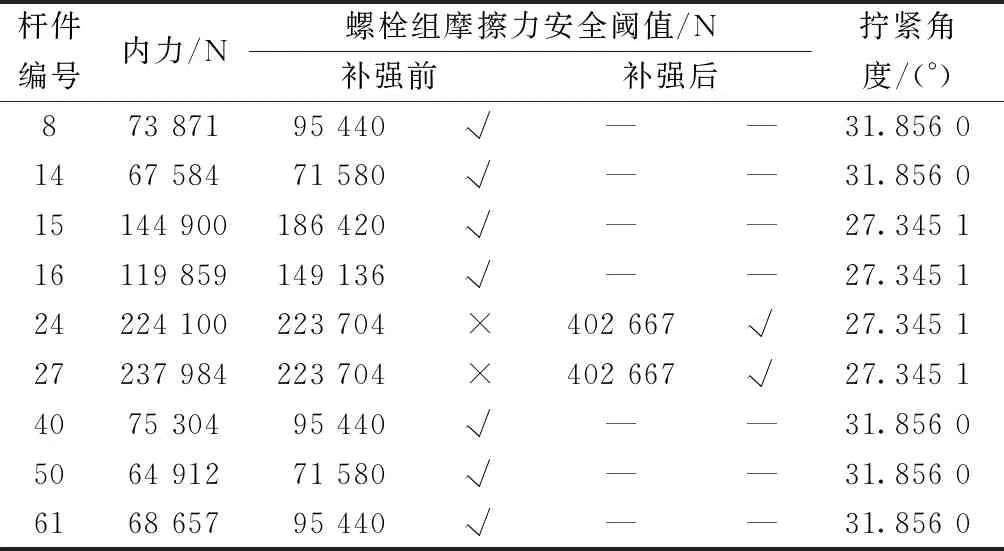
表5 螺栓组校验及补强分析

由表5可知，杆件24、27的原螺栓组所提供的预紧力不足，引发螺栓松动致使铁塔倒塌，再采用等厚双帽防松螺栓补强后，螺栓组所提供的预紧力满足要求。最后按照安全情况下的螺栓组计算螺母的拧紧角度，结果表明M20×2螺母、M16×1.5的拧紧角度分别为31.856°和27.345 1°。

4 结论

(1)针对输电铁塔内力计算模型的不足，引入n次超静定结构的力法方程对杆件内力进行求解。以500 kV宜兴Ⅰ回线路141#为例，建立了更符合实际的全塔1/4模型，计算结果与仿真值吻合良好，且偏差均小于10%，验证了本文方法的正确性。

(2)基于杆件内力的求解结果，得到了覆冰舞动条件下猫头塔的薄弱区域分布，并进一步对螺栓组的连接强度进行校验，研究结果与实际情况一致，同时，提出的补强措施可以满足工程需求，对今后的舞动区铁塔设计和改造具有一定的指导意义。