基于长短时记忆与多影响因子的滑坡位移动态预测
李丽敏, 郭 伏, 温宗周, 陈鹏年, 张顺锋
(西安工程大学电子信息学院, 西安 710600)
滑坡灾害严重威胁国家和人民的安全,因此滑坡预测预警显得尤为重要。位移作为滑坡灾害的一个宏观表征,长期以来被中外学者作为滑坡预测预报的关键参数。目前对位移预测的方法主要有:一是将研究区观测点累计变形位移分解为受内在因素影响的趋势性位移与受外界因素影响的周期性位移或波动性位移,并分别对其进行建模预测,最终将以上两项预测值相加得到累计位移预测值[1]。该方法考虑了滑坡体变形的演化机制,但没有切实考虑滑坡体演化过程中的动态特性。檀梦皎等[2]利用自适应噪声完整集合经验模态分解法将滑坡体变形位移分解为趋势项位移和波动项位移,并对其进行预测;李骅锦等[3]考虑到滑坡体变形成因,分别对趋势项与周期项进行预测,预测效果相对较好。二是通过建立研究区位移特征影响因子与位移之间的预测模型,从而获得预测位移。该方法能够根据滑坡体变形特征与变形位移之间的相关性,在减少运算量的同时进一步提高了预测精度,但为避免时间复杂度,其所选影响因子不够全面。徐峰等[4]将滑坡位移分解为受其自身基础地质条件控制的趋势项位移以及由外界因素(如降雨、库水位变动等)影响的周期项位移,应用时间序列分析方法建立滑坡位移预报模型。可见该方法对滑坡灾害位移预测研究具有一定的促进意义。
近年来,多项式拟合、神经网络、极限学习机、机器学习等智能算法因其具有较强的非线性映射能力以及可实现任意精度的函数逼近等优势,从而被众多学者广泛应用于地质灾害预报预警领域,并取得了一定的成果[5]。然而在以往的滑坡位移预测案例中使用的BP(back propagation)、ELM(extreme learning machine)等模型属于静态网络,没有考虑滑坡自身演变的动态特性,不能反映滑坡变形的演化过程,预测效果不佳。为此,有关学者提出了一种动态神经网络-循环神经网络(recurrent neural network,RNN),因其具有记忆信息的能力从而用于对时序数据的处理和预测。然而在实际应用中由于RNN本身的结构特点,使其只能记忆上一时刻或者邻近时刻的信息,对于较远时刻的信息无法保留,导致RNN在训练时存在梯度消失或梯度爆炸问题[6],致使模型精度不够,预测结果不准确。为解决该问题,Hochreiter等[7]在RNN的基础上,提出了长短时记忆神经网络(long short time memory,LSTM),引入一个单元状态(c)以及“门”解决了RNN存在的梯度消失或梯度爆炸的问题,LSTM在其他领域也取得了一定的成就。朱肖颖等[8]基于LSTM算法在新闻分类中对原始数据展开格式变换、分词加工后,进行特征提取并建立LSTM网络模型,解决了在海量新闻数据下RNN存在的梯度消失问题,LSTM算法表现出了较高的模型准确度和良好的扩展性;王森等[9]基于LSTM-RNN的质子交换膜燃料电池故障检测方法,以LST包和6种常见异常数据构建时序序列LSTM模型,并通过贝叶斯优化获取最佳参数,结果表明,LSTM在对燃料电池故障分类的准确率达95%以上。可见LSTM在诸多领域应用中表显出一定的优势,因此考虑将其应用于地质灾害预报领域。
现以新滩滑坡为例,首先将滑坡监测点累计位移分解为趋势项与波动项;随后,采用多项式拟合预测趋势项位移,灰色关联度筛选外界因子后利用LSTM预测波动项位移,并与RNN及传统静态预测模型BP、ELM进行比较,使用均方根误差(RMSE)、平均绝对百分比误差(MAPE)、拟合优度(R2)分别对其进行评价,验证本文模型的优越性。最后,叠加周期项与波动项,得到滑坡累计位移。
1 滑坡位移预测模型
1.1 位移时间序列分解
滑坡体变形位移因山体内部复杂的地质构造以及外部诱发因素的共同影响,其增长方式表现为非线性。研究表明,滑坡累计位移时间曲线可分解为3项[3]。①趋势项:在坡体内部(地形地貌、地层岩性等)环境作用下,滑坡位移表现为随时间变化的近似单调增函数[10];②波动项:受地场环境(季节性降雨、地表水位等)因素作用产生的波动性位移[10];③随机项:诸如人类活动、植被覆盖率、地震等突发性事件作用所产生的响应位移;由于监测手段的限制,目前只考虑滑坡体趋势项位移与波动项位移,基于以上分析,根据时间序列加法模型将滑坡累计变形位移时间曲线分解为
St=ωt+ψt
(1)
式(1)中:St为滑坡体变形总位移;ωt为趋势项位移;ψt为波动项位移。
通过历史数据进行模型训练,并将各监测点数据输入模型中进行预测。采用多项式拟合预测趋势项位移,在对波动项位移进行预测时引入外界诱发因子,通过灰色关联度提取主要相关因子,并将其作为LSTM预测模型初始输入。其具体流程如图1所示。
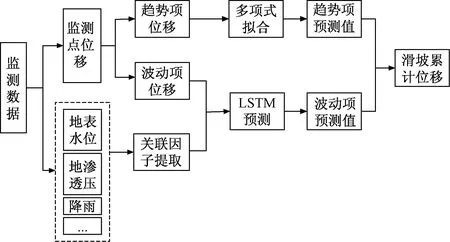
图1 技术路线图Fig.1 Technical roadmap
1.2 RNN与LSTM算法描述
1.2.1 RNN基本原理
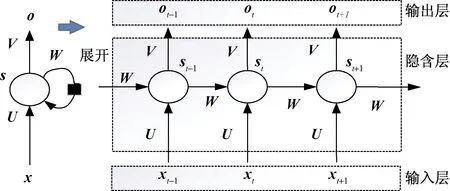
图2 RNN网络结构Fig.2 RNN network structure
图2为RNN结构图。图2中,该网络分为3层:输入层、隐藏层、输出层[11]。其中x为输入层的向量,s为隐藏层的向量[12],o为输出层的向量。输入层与隐含层之间的U为连接输入层到隐含层的权重矩阵;W为隐藏层的权重矩阵;V为隐藏层到输出层的权重矩阵[13]。
RNN网络在t时刻接收到输入xt之后,隐藏层的输出值是st,输出层的结果是ot[14],st的结果不仅取决于xt,还取决于st-1。RNN计算公式为
ot=g(Vst)
(2)
st=f(Uxt+Wst-1)
(3)
式(2)表示输出层ot的计算过程,它的每个节点都和隐藏层的每个节点相连;Vst为输出层的权重矩阵;g为激活函数;f为激活函数。式(3)表示隐藏层的计算过程。
1.2.2 LSTM基本原理
传统RNN,每个重复的模块里都有一个简单tanh层。LSTM属于一种特殊的RNN,两者差异在于每个模块中的结构不相同,LSTM拥有4个网络层,以一种特殊方式相互连接。如图3所示为RNN与LSTM结构对比。
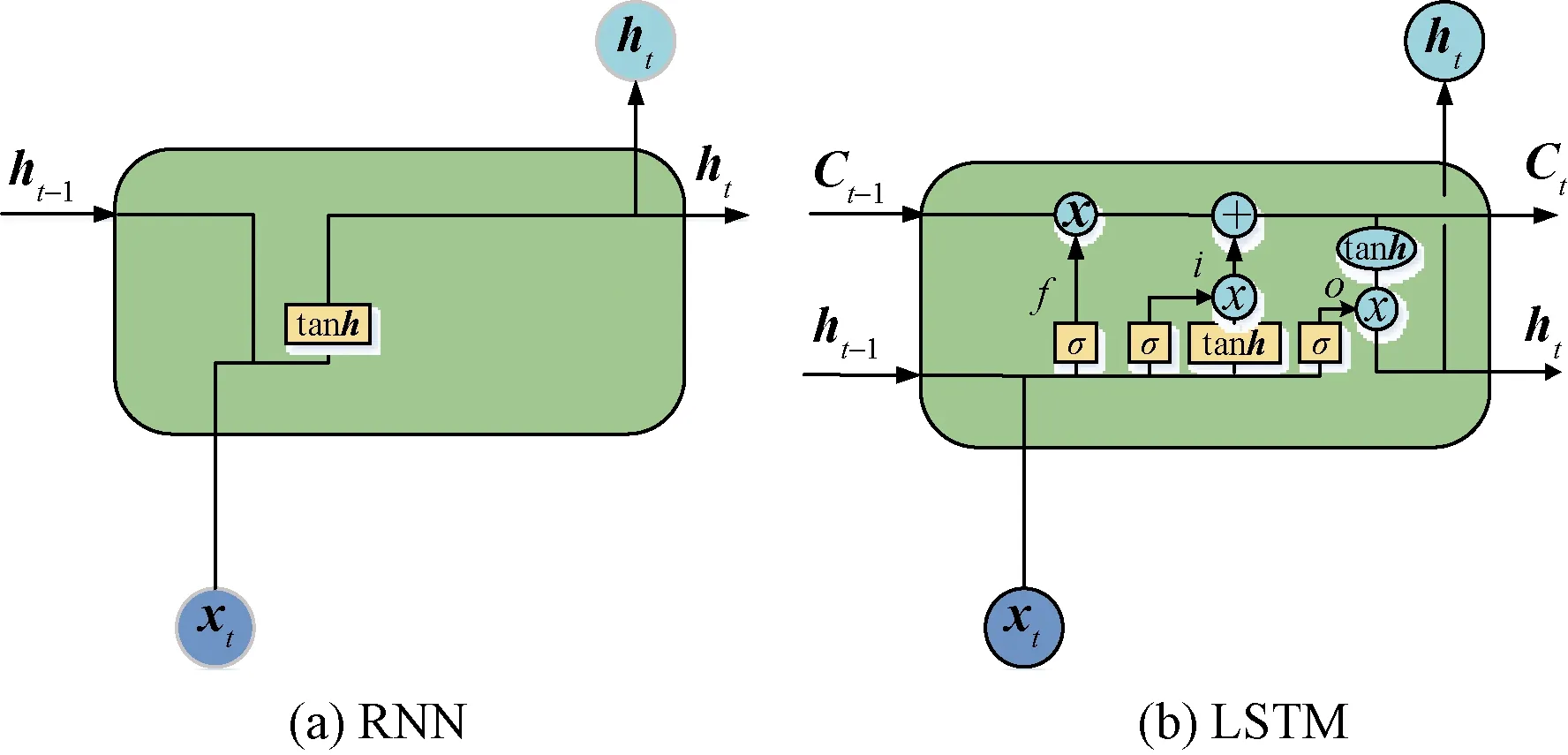
图3 RNN与LSTM结构图Fig.3 RNN and LSTM structure
由图3可以看出,LSTM网络结构在RNN原有的基础上增加了单元状态c,并引入“门”,其目的是解决RNN网络中的梯度爆炸和梯度消失问题。LSTM的主要结结构算法:
ft=σ(Wf[ht-1,xt]+bf)
(4)
it=σ(Wi[ht-1,xt]+bi)
(5)
(6)
(7)
ot=σ(Wo[ht-1,xt]+bo)
(8)
ht=ot∘tanhct
(9)

图4为LSTM动态建模算法流程,首先进行初始化,包括学习速率、各层之间的初始权重值、期望精度等;然后输入给定向量值,求出目标输出值并与给定值进行偏差计算,判断其是否满足误差精度要求,否则对所有各层之间权重进行更新,直到偏差满足预期给定期望值时,迭代停止,训练结束。
基于LSTM算法本身结构的独特性,使其在对长时序数据进行处理时具有较强的能力,因此使用LSTM算法对波动项位移进行预测,更能有效地表征滑坡体变形的过程。
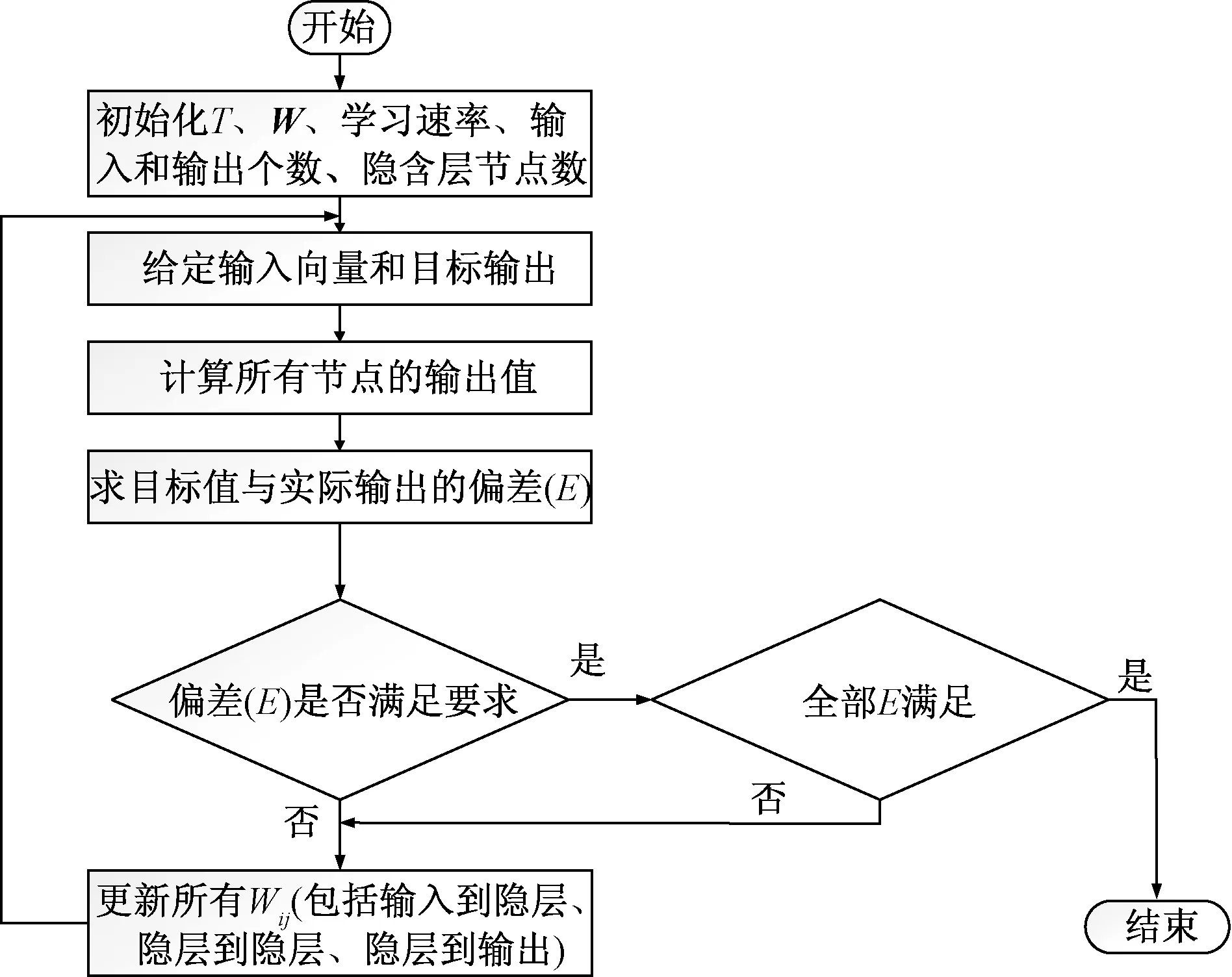
T为初始期望精度;W为初始权重;E为各层之间的偏差图4 LSTM训练流程图Fig.4 LSTM training flow chart
1.3 模型精度评价
采用平均绝对百分比误差(MAPE)、均方根误差(RMSE)与拟合优度(R2)对预测模型进行评价。MAPE表示预测值较真实值平均偏离的程度(单位:%),MAPE越接近于0,则表示预测值平均偏离真实值越小,预测效果越好。RMSE反映预测值同真实值之间的偏差,RMSE越接近于0,则表示预测值与真实值越吻合。拟合优度(R2),也称决定系数,直观反映变量对相应变量的解释程度或密切程度,R2越接近于1,说明模型观测值的拟合程度越好。MAPE、RMSE与R2的计算公式为
(10)
(11)
(12)

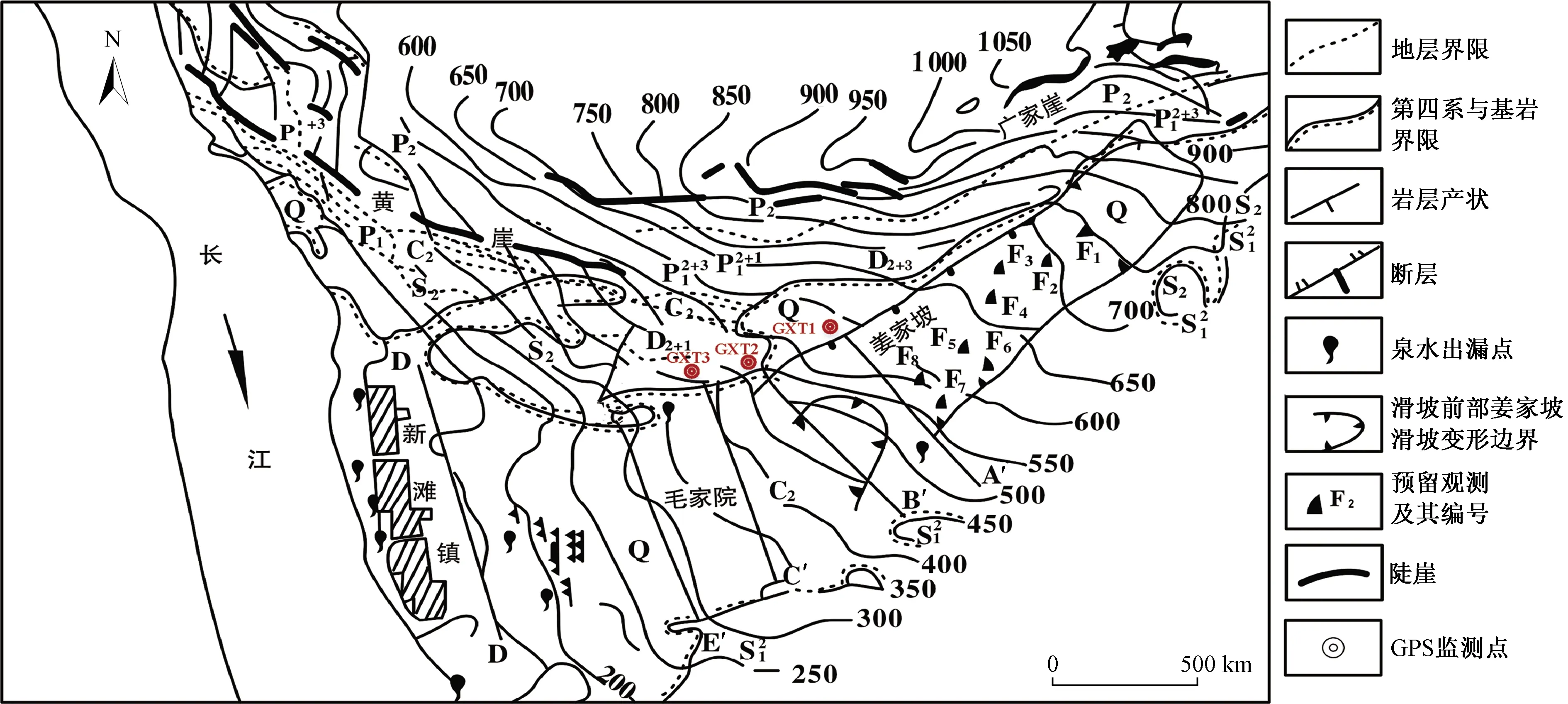
Q为第四系冲积层、崩积层、坡积层;P2为二叠系上统灰岩;为栖履组与第四组灰岩;为马鞍山煤组岩层;C2为黄龙灰岩; D2+3为泥盆系石英砂岩;S2为志留系砂页岩;为页岩;A—A′为观测及其编号;1为地层界限;2为第四系与基岩界限;3为岩层产状; 4为断层;5为泉水出漏点;6为滑坡前部姜家坡滑坡变形边界;7为预留观测及其编号;8为陡崖;9为GPS监测点图5 新滩滑坡平面图Fig.5 Plan of Xintan Landslide
2 应用与分析
2.1 新滩滑坡概述
新滩滑坡属于姜家坡-新滩堆积层老滑坡。新滩滑坡所处河段为横向谷,岩层倾向上游略偏北岸,倾角为25°~38°[16],老滑坡西侧紧邻坚硬的泥盆一二叠系砂岩和灰岩组成的陡崖,300~450 m,是堆积层物质的主要来源;东侧为志留系页岩组成的低山丘。滑坡后缘高程约900 m。向南延伸至江边高程约65 m,平均坡度23°。滑前坡体中部有两级横向陡坎,一是高程500~560 m的姜家坡前缘陡坎。走向NE30″,坡度50°~60°,将斜坡分为上段(姜家坡斜坡)和下段(新滩斜坡)[17];二是陡坎在毛家院前缘,高程为270~330 m,走向NE75″,将新滩斜坡分为毛家院台面和陡坎下两段,图5为新滩滑坡平面图。
2.2 变形成因分析
图6为2003—2007年5个监测点(GXT1、GXT2、GXT3、GXT4、GXT5)滑坡累计位移时序曲线图,纵观5个监测点可以看出每年5—11月滑坡累计变形位移波动较大,整体呈现增长趋势;图7为滑坡前缘GXT4监测点累计变形位移时间及月降雨数据,从图7可以看出,在降雨季,滑坡变形位移随着雨量强度的增加,呈非线性增加的趋势,如2004年1—4月,滑坡总降雨量为246.8 mm,对应的变形位移最大增量为2.037 mm,位移速率0.679 mm/月,但从5—11月滑坡变形位移最大增量为11.436 mm,总降雨量超过了700 mm,位移速率达到了1.89 mm/月。而从2004年11月开始,滑坡位移又随着降雨量的减少进入相对稳定的时期。以上分析表明滑坡的位移量与降雨具有很强的相关性[18]。
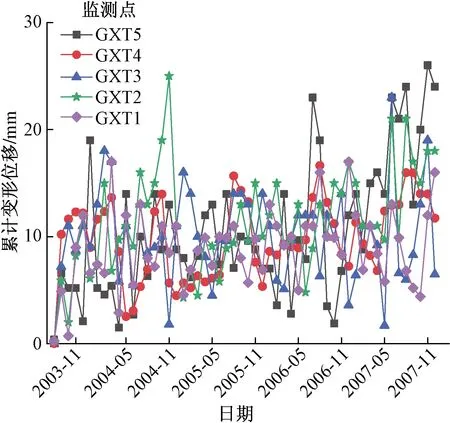
图6 各监测点累计变形位移Fig.6 Accumulated deformation displacement of each monitoring point

图7 GXT4累计变形位移时间及月降雨数据Fig.7 Accumulated deformation displacement time and monthly rainfall data of gxt4
同时,根据新滩滑坡监测资料和调查记录,受区域性地壳抬升和河谷深切的影响,滑坡区崩塌活动严重。北侧的广家崖及姜家坡属于强烈卸荷区,经常发生较大规模的崩塌,例如1935年姜家坡前缘东侧发生1.5×106m3局部滑坡,滑床已深达基岩;1962年后壁以上出现长270 m的拉张裂缝;1964年秋季西侧发生南北向450 m长大裂缝;加上耕种、采煤等人类活动,加速了滑坡的失稳破坏。从以上的分析可知,新滩滑坡同时受到波动性因素(降雨等)和随机因素(人类活动等)的影响,可用时间序列非线性组合模型对滑坡位移数据进行分析[18]。选用2003年7月—2008年1月GXT4监测点累计变形位移数据进行建模,其中2003年7月—2007年1月数据集作为训练样本,2007年2月—2008年1月数据集用于预测及验证。
2.3 趋势项位移预测
采用移动平均法提取趋势项位移,移动平均法可以消除因周期项波动与随机项波动而不能显示出事件的发展趋势的问题,其主要思想是根据时间序列、逐项推移,依次计算包含一定项数的时序平均值,从而反映长期趋势,如式(13)所示:
Ft=(At-1+At-2+…+At-n′)/n′
(13)
式(13)中:Ft为对下一期的预测值;n′为移动平均的时期个数;At-1为前期实际值;At-2、At-3与At-n′为前两期、前三期、前n期的实际值。
趋势项位移提取结果如图8所示,为消除不同量纲之间的影响,需将位移数据归一化到[0,1]区间,随后采用3次多项式对趋势项位移进行预测,如式(14)所示:
y=d1t3+d2t2+d3t+d4
(14)
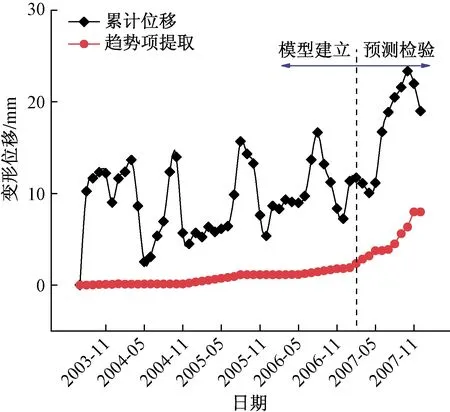
图8 趋势项位移提取Fig.8 Displacement extraction of trend term
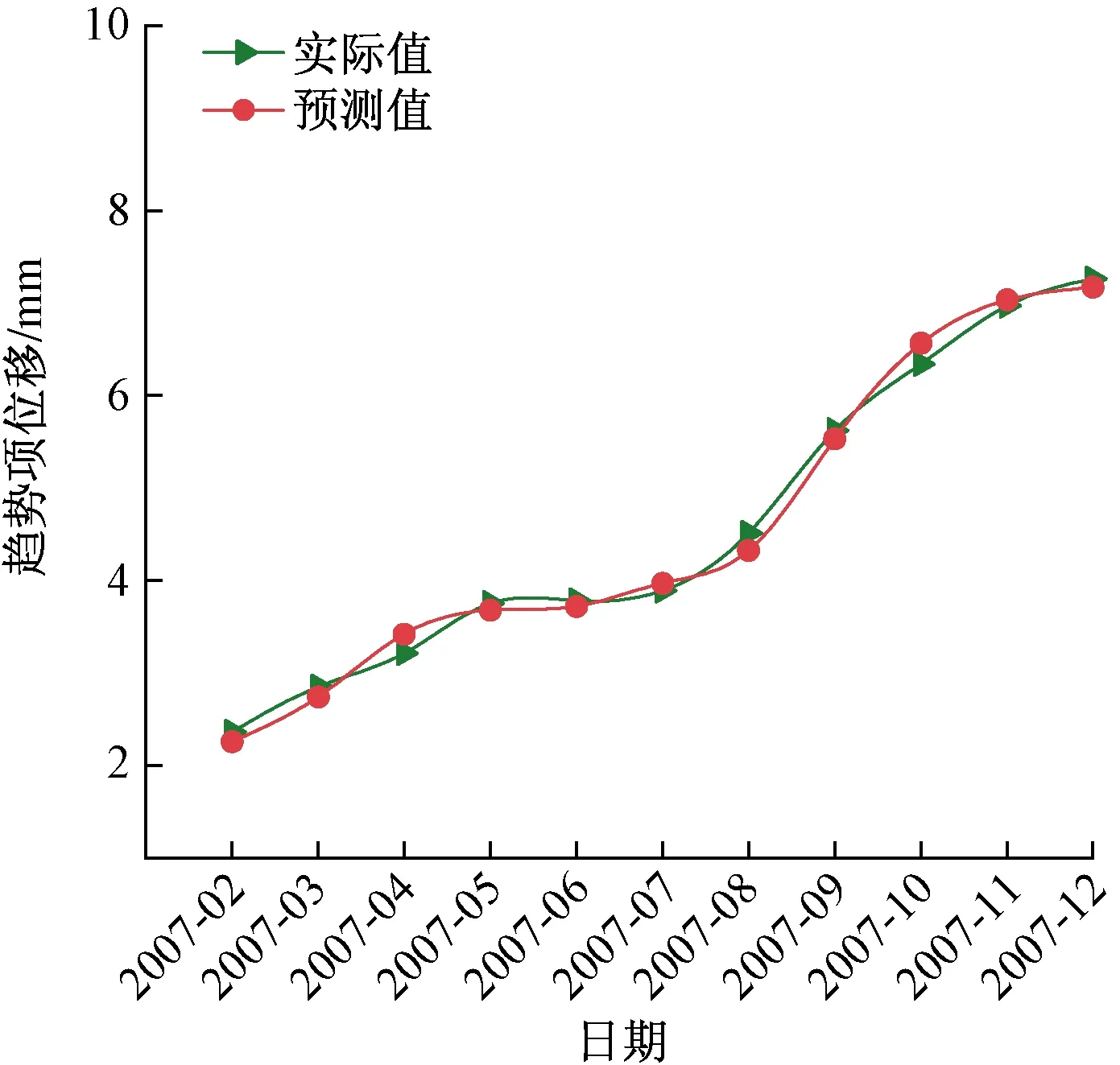
图9 趋势项位移预测Fig.9 Displacement prediction of trend term
式(14)中:y为趋势项位移预测值;d1、d2、d3、d4为多项式系数,采用最小二乘确定多项式各系数后并进行训练,在实际训练中,将前一期次的位移预测值加入训练样本重新拟合,并预测当前期次位移;趋势项位移预测结果如图9所示,对比趋势项位移与拟合预测位移可知,将上一期次趋势项位移预测值加入训练集中,实现滚动预测,促使模型不断更新,能够更进一步提高模型预测精度,其中MAPE为2.79%,RMSE为0.13 mm,R2为0.963,预测效果较好。
2.4 波动项位移预测
利用滑坡原始累计变形位移减去趋势项位移即可得波动项位移,若直接将波动项位移作为预测模型输入,而不考虑外界诱发因素对滑坡位移的响应,则会使预测结果不准确[19]。因此在对新滩滑坡进行实地调研并收集全周期监测外界诱发因素数据(降雨、地表水位、地渗透压、土壤含水率、坡度等)的基础上,结合滑坡累计位移时间数据分析确定对波动项位移影响较大的因子,并将其作为预测模型的输入。
2.4.1 影响因子筛选
新滩滑坡研究表明,降雨能否诱发滑坡,不完全取决于降雨强度与大小,还在于滑坡所处的发展阶段,在滑坡条件尚未成熟时,久雨、暴雨也不能造成整体滑动;在临滑阶段,只要是可形成地下水活动的低水平降雨也能成为诱发因素。因此,拟选取降雨x1(单位:mm)、地表水位x2(单位:mm)、孔隙水渗透压x3(单位:kPa)、土壤含水率x4(单位:%)、坡度x5(单位:°)、坡高x6(单位:m)、堆积物自重x7(单位:N)、后缘荷载x8(t)8个影响因子共90期数据集,如表1所示。采用灰色关联度[20]筛选出主要影响因子并将其作为模型初始输入,具体步骤如下。
Step 1构建[m,l]维矩阵X′i=[x′i(1),x′i(2),…,x′i(m)]T,i=1,2,…,l,l为因子类型个数,m为期数。
Step 2确定参考序列X′0=[x′0(1),x′0(2),…,x′0(m)],其中x′0(m)为0~90期波动项位移量。
Step 3采用均值法对各影响因子数据及参考序列进行无量纲化,如式(15)所示:
(15)
Step 4逐个计算每个影响因子对象与参考序列对应元素的绝对差值|x0(k)-xi(k)|,(k=1,2,…,m;i=1,2,…,l)。
Step 5计算关联系数ζi(k)及关联度ri。
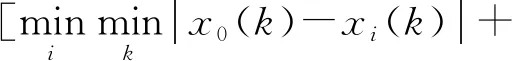
(16)
(17)
式中:k=1,2,…,m;ρ为分辨系数,通常取值为0.5,提取后各影响因子关联度如图10所示。

图10 影响因子关联度Fig.10 Correlation degree of influence factors
由图10可知,8个影响因子的关联度分别为86.236%、67.571%、42.183%、68.299%、22.645%、14.265%、63.434%、65.856%。当诱发因素与滑坡位移关联度超过0.6[21],认为该因素对滑坡变形有着较强的促进作用。灰色关联度采用数据驱动的方法,通过大量的数据计算来探寻事物间的内在联系,而数据驱动算法对待数据具有平等性。杨背背等[5]采用灰色关联度对白水河滑坡进行影响因子筛选,预测效果较好;黄健等[22]在对垮梁子滑坡变形成因分析中以灰色关联度筛选最优影响因子,预测精度较高;李仕波等[23]利用灰色关联度筛选外界诱发因子,在对台阶状位移特征滑坡案例中采用LS-SVM模型进行预测,模型预测精度较高。因此剔除坡度、坡高、渗透压3个因子,将降雨、地表水位、土壤含水率、堆积物自重、后缘荷载以及波动项位移作为预测模型的输入,保证了数据在实际应用中的相对合理性。
2.4.2 模型建立及参数选取
采用LSTM模型与RNN对波动项位移进行预测,并与传统神经网络BP、ELM做对比验证采取模型的优越性。其中70%的数据用于模型训练,30%的数据用于验证,如图8所示。将筛选后的外界影响因子及波动项位移归一化到[0,1]区间作为预测模型的输入,波动项位移作为输出。利用Keras框架与TensorFlow后端支持搭建模型,本文模型中输入层节点数为12,输出层数为1,使用果蝇算法[24](FOA)对LSTM网络隐藏层节点数进行寻优,结果表明当隐藏层数为18时,LSTM模型具有更高的精度。
2.4.3 波动项位移预测结果对比分析
采用已在滑坡位移预测方面具有较好应用的BP、极限学习机(ELM)神经网络进行模型对比评价。以粒子群优化(PSO)算法对BP神经网络的初始权值和阈值进行优化,粒子群优化算法(particle swarm optimization,PSO)参数设置:粒子群规模N=40,粒子群迭代次数为246,加速常数c1=1.59,c2=1.463 84,粒子位置最大值为1,最小值为-1,粒子维度空间d=206;ELM神经网络采用Sigmoid核函数,最佳隐含层神经元个数为28[25]。
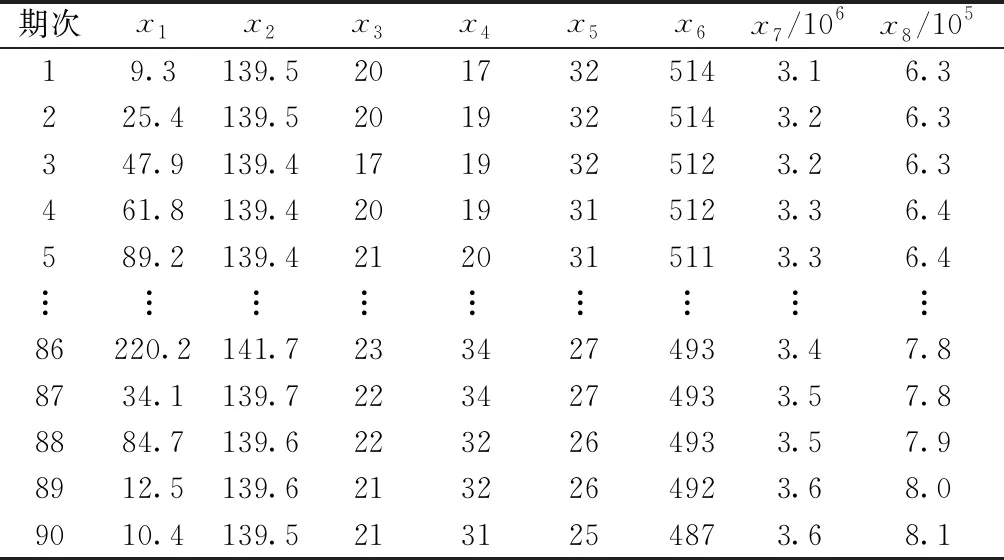
表1 各影响因子参量矩阵
图11为波动项位移预测结果,2007年5—11月位移波动较大,其中2007年5—7月由于主要外界诱发因素降雨量增多,位移呈现出非匀速增长趋势;2007年8—10月随着降雨量的减少,位移增长趋势逐渐缓慢;2007年11月—2008年1月,由于外界降雨以及地表水位的增幅基本相对较小滑坡变形位移整体呈现下降趋势。从图11可以看出,滑坡变形位移在整个非线性变化过程中BP与ELM神经网络对外界诱发因素所产生的波动性位移预测效果较差;RNN与LSTM模型预测值均与实际波动项位移的变化趋势一致,预测效果相对稳定,能较好地反映滑坡体受外界诱发因素所产生的波动性位移。
由表2可知,RNN与LSTM两种模型在预测某一期波动项位移时,RNN预测所用时间比LSTM要快约50倍,但LSTM预测模型的拟合优度R2为0.95高于RNN、BP、ELM神经网络,其平均百分比误差MAPE为1.856%、均方根误差RMSE为0.324 mm均小于其他神经网络。究其原因,LSTM为解决RNN在处理长时序数据时产生的梯度爆炸或梯度消失现象而引入了“门”以及其算法内部结构、参数的复杂,使其在处理长时序数据的能力大大提高,相应地LSTM的计算时间也会增加。而在本次滑坡位移预测实例中,各模型预测所需的计算时间可忽略,因其位移的演化是一个逐渐累积的过程,需要的时间远大于计算机预测所需的时间。
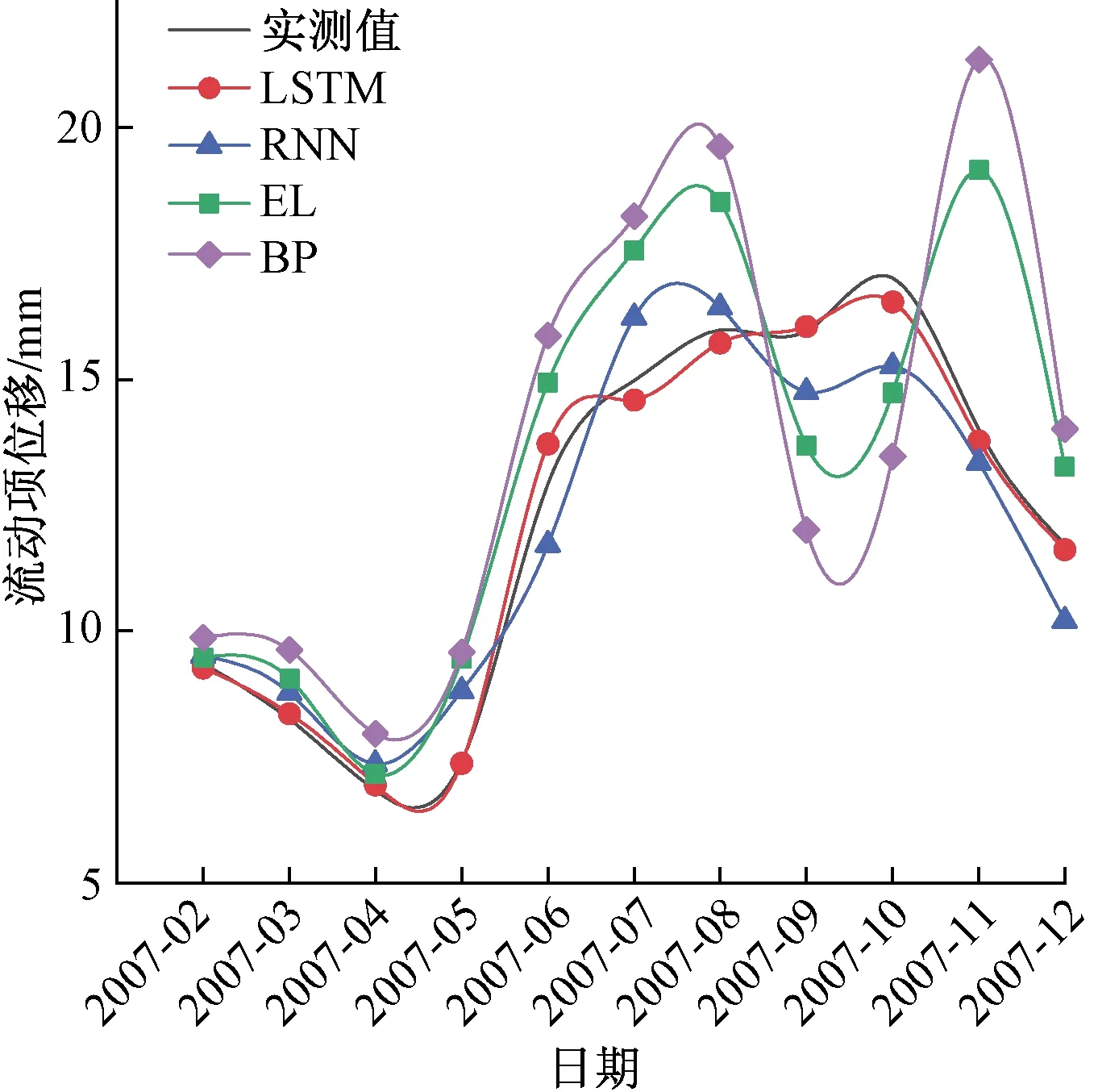
图11 波动项位移Fig.11 Wave term displaceme
因此,引入外界影响因子的 LSTM 神经网络模型较其他预测模型,预测结果更优,且在描述滑坡变形趋势与规律上更加稳定,更适用于滑坡位移预测 。
2.5 累计位移预测结果
将预测所得趋势项位移与波动项位移进行累加得到最终累计变形位移,如图12所示,2007年与2008年中,每年5—11月滑坡变形位移受外界因素而波动较大,所采用的LSTM模型预测位移与实测位移吻合度较高,其中RMSE为0.327 mm,MAPE为1.026%,拟合优度R2为0.978。
为进一步验证本文模型的科学性与适用性,采用训练后的LSTM模型对2008年位移进行预测,以滑坡实际监测点位移作为验证数据集。从图12中可以看出LSTM模型预测值与实际监测位移一致性依然较高,可见,LSTM动态神经网络预测的滑坡位移精度较好,能够较好地表征滑坡体变形演化过程。

表2 各模型预测结果及评价指标Table 2 Prediction results and evaluation indexes of each model

图12 累计变形位移Fig.12 Accumulated deformation displacement
3 结论
以滑坡体变形位移为研究对象,同时引入外界影响因子,采用LSTM神经网络对新滩滑坡GXT4监测点进行分析预测,得出如下主要结论。
(1)将滑坡累计变形位移分解为受内部演化的趋势项与外界诱发因素导致的波动项。趋势项位移与波动项位移均表现出良好的趋势性;相较于原有的RNN与传统的静态神经网络BP、ELM预测模型,采用动态神经网络LSTM预测模型对外界诱发因素所产生的波动性位移具有良好的反应能力,平均百分比误差MAPE为1.026%,均方根误差RMSE为0.327 mm,拟合优度R2为0.978。
(2)灰色关联度筛选出对波动项位移具有较大促进作用的外界因子为降雨、地表水位、土壤含水率、堆积物自重、后缘荷载;此外,LSTM模型相较于原有的RNN模型预测精度更高,但其计算时间比RNN慢,而计算机训练耗时在滑坡位移预测中可忽略。究其原因,LSTM独有的内部结构,以及众多参数使其在提高进度的同时也耗费了计算时间。
(3)滑坡预测的结果可转化为滑坡风险预测,因此LSTM动态预测模型对滑坡预测预报研究具有一定的促进意义。此外,滑坡体演化所处不同阶段时选用的预测模型对预测精度也有一定的影响,所使用的方法是相对于滑坡体变形的整个演化过程,没有考虑滑坡体演化所处阶段进而选用相应有效的预报模型,因此对滑坡体变形阶段的划分与进一步选用适当的预测模型,最终实现临滑点的预报是下一步研究的重点。

