高含水旋转湍流场中油滴分散特性的数值模拟

田洋阳，张春影，牛振宇，何利民

（1.中国石油大学（华东）储运与建筑工程学院，山东青岛266580；2.西安石油大学石油工程学院，陕西西安710065；3.西安长庆科技工程有限责任公司，陕西西安710018）

旋转湍流场在各类流体机械（如泵、风机、压缩机、旋流器）中广泛存在，其中涉及气相、液相等多相的流动与分离[1-4]，液液流动并未受到像气液流动被广泛的关注，其密度差非常小，黏度比变化较广，且呈现出牛顿或非牛顿流体的流变特性。因此，许多气液两相的理论和结果都无法直接应用在液液两相流动中。

液滴形成机制和特征尺寸对分析液液分散相流动中的流体力学和输运现象是非常重要的。通常，旋转湍流场中液滴的尺寸分布取决于液滴破碎和液滴聚结两个过程，其都与液滴周围的湍流场的速度有关。在分散相浓度很高的情况下，液滴的聚结过程必须考虑；但当含油体积分数小于10%时，液滴的特征尺寸由液滴破碎机制控制[5]。

湍流外力趋向于使液滴变形和破碎，动态压力对液滴尺寸影响最大，其是由与液滴尺度相等的距离内的速度变化引起，与液滴周围的湍流场的速度有关。但是，湍流是随机且不可准确预测的，甚至在单相流场中也是如此。分散流中液滴与连续相中的湍流涡相互作用方式很多，其取决于液滴和涡的相对尺度。这些相互作用通常伴随着液滴和涡运动的变化，会进一步影响液滴的破碎。

综上获得准确的旋转湍流场中液滴尺寸分布难度非常大，根据笔者调研可知，湍流场中液滴尺寸分布问题的研究较成熟，其中最具代表性的是搅拌器中两相体系分散相的破碎。G.I.Taylor[6]研究了黏性力引起的液滴破碎，建立了最大稳定粒径关系式。J.O.Hinze[7]研究了惯性力引起的液滴破碎，首先提出了当液滴的直径大于耗能微团的尺度时湍流场中液滴破碎的判据，并建立了各向同性并且均匀湍流场中最大稳定液滴直径的表达式，该模型至今仍被广泛采用。F.B.Sprow[8]根据液滴直径大小与湍流涡尺寸之间的关系，建立了Dmax的最大稳定液滴直径表达式。C.Tsouris等[9]建立了含有分散相黏度项的最大稳定粒径的表达式。J.Han等[10]采用两相的密度比在0.01到1.0，通过直接模拟证实了当分散相密度接近连续相密度时，临界韦伯数Wec会增加。

关于旋转湍流场内液液体系中分散特性的研究较为有限，S.Liu等[11]研究了安装有导叶的管道内的油滴破碎和聚结的规律，对Kubie和Gardner的最大稳定液滴模型与数值模拟结果对比，结果较为吻合，数值模拟获得的最大液滴尺寸分布在理论预测模型的曲线周围，但文中并未提出新的预测模型。D.Eskin[12]对分散相体积分数小于10%时同心旋转圆筒装置展开研究，采用群体平衡方法获得了油滴的尺寸分布，并通过实验验证。M.Dressler等[13]对聚合物在同心旋转圆筒装置内的分散情况进行研究，确定产生非常均匀的液滴分布下的最佳操作条件。与带有导叶的管道内的液液分散体系相比，通过控制内外筒的间隙尺寸的同心旋转圆筒装置可以获得均匀分布的流场，为分散特性的研究带来极大的便利，因此本文利用数值模拟的方法，采用新型的同心旋转圆筒装置（内筒、外筒间隙尺寸为5 mm，且外筒顶面和底面上分别设置上环形出口和下环形出口），为旋转湍流场内液液分散特性提供新的研究思路，完善了液-液两相体系中分散特性的研究。

1 数值模拟策略

1.1 几何模型

该装置的内筒内径（直径）为126.9 mm，筒高为62 mm，流体区域为内筒与外筒之间的间隙部分，上下间隙与侧面环形间隙均为5 mm；入口管直径为5 mm，入口管设在圆筒的中间位置，高度为31 mm，流体沿切线方向流入；外筒顶面和底面位置分别设有环形出口，截面尺寸均为2 mm，结构示意如图1所示。

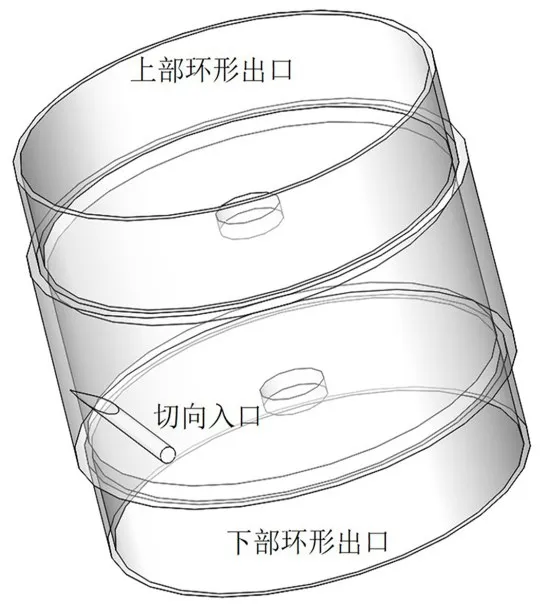
图1 同心旋转圆筒装置示意Fig.1 Schematic diagram of concentric rotating cylinder device

1.2 湍流模型

数值模拟计算的关键是根据待求解问题中流场的特性选择合适的求解模型，本文中湍流模型选择标准k-ε模型，通过对两个单独的方程进行求解来确定流场中的湍流长度和时间尺度。该模型在计算过程中具有较好的稳定性、经济性以及较为合理的计算准确性，对多种情况下湍流流动具有广泛的适应性[14-16]。

模型中的湍流动能方程k和扩散方程ε可以用式（1）、（2）表示[17]：

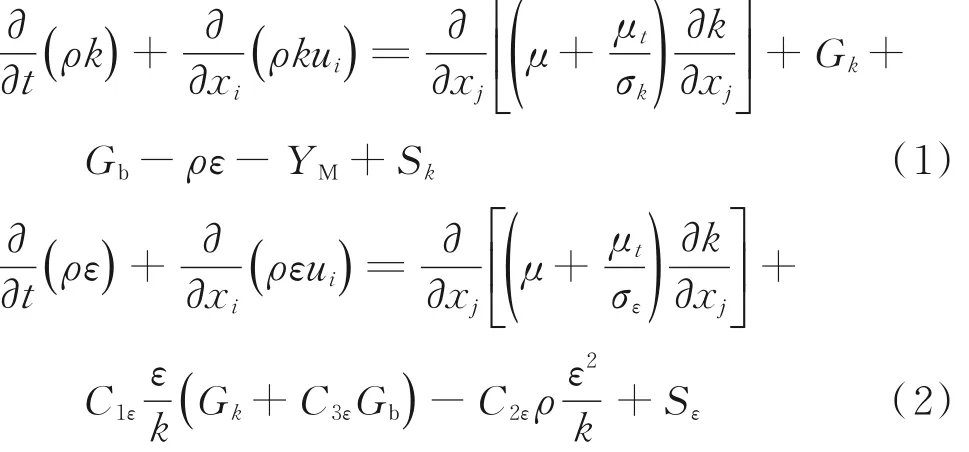
式中，k为湍动能，J；ε为湍流耗散率，m2/s3；ρ为流体密度，kg/m3；μt为湍流黏度，m2/s；Gk为由于层流场中的速度梯度发生变化所引起的湍流动能，J；Gb为受到浮力的影响产生的湍流动能，J；YM为在可压缩的湍流流场中产生的波动影响；C1ε、C2ε、C3ε为常数；σk和 σε分别为上述两方程中的湍流 Prandtl数；Sk和Sε为用户自行定义的数值。

1.3 离散相模型

离散相模型（DPM，Discrete Phase Model）是在拉氏坐标下对流场中的分散相进行数值模拟计算，通过对分散相颗粒所受到的力的方程进行积分，来求解分散相颗粒在流场中的运行轨迹，获取运动迹线图。采用泰勒类比（TAB，Taylor Analogy Model）模型进行计算是研究液滴破碎问题中较为常用的计算方法[18-19]，最早是由Taylor提出的，他将液滴的振荡变形近似看成弹簧系统，利用TAB模型中的方程组可以分析流场内液滴的振荡和扭曲现象，能够确定任何给定时间下流场内液滴的振荡和变形情况。本文中油相体积分数小于10%，故采用DPM模型和TAB模型求解油滴的分散特征。

1.4 网格划分

采用ICEM软件对流体域进行了非结构化网格划分，网格类型采用四面体混合网格，网格划分方法采用Robust(Octree)，网格划分结果如图2所示。

图2 同心旋转圆筒装置网格示意Fig.2 Grid diagram of concentric rotating cylinder device

为了消除网格数量对计算结果的影响，划分了三种不同数量的网格，分别为647 156、1 619 489和3 278 152。选取圆筒壁距离下部环形出口y=31 mm处XZ截面上过轴心的一条直线上的湍流耗散率ε作为研究对象，进行网格无关性验证，验证结果如图3所示。当网格数量由647 156增加到1 619 489时，所取直线上的湍流耗散率ε值有了较大变化，当再次提升网格数量时，其计算结果无较大区别。所以本文采用1 619 489的网格数量，既确保数值模拟结果不受网格数量的影响，又能够减少计算量。

由图3可知，实验装置内的湍流耗散率分布比较均匀，主流区域的湍流耗散率约为20 m2/s3，仅在内外筒壁面上湍流耗散率较大，这是由于在近壁区湍流脉动受到壁面的抑制，湍流结构非常复杂，逆序结构较为活跃，小尺度上的湍流耗散比较明显。由于环隙内雷诺数较高，可以达到105，湍流边界层非常薄，对整体的流动状态影响较小。

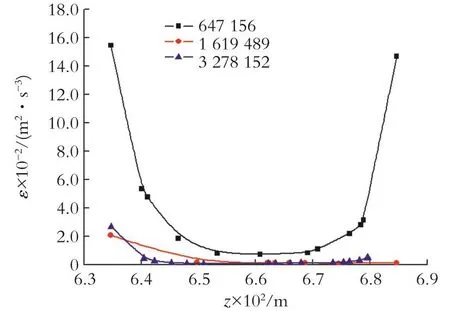
图3 网格无关性验证Fig.3 Grid independence validation

1.5 数值解法及边界条件

数值模拟采用商业软件Fluent，其中计算所采用的油水混合物，在单相场的数值模拟中，介质为水相，密度为998.2 kg/m3，动力黏度为0.001 003 kg/(m2·s-1)。装置的进口位置采用速度进口，进口流速为0.865 339 m/s，上下出口均采用速度出口，上部出口的流量权重设为0.1，下部出口的流量权重设为0.9。压力速度耦合采用SIMPLE算法，压力的离散格式采用PRESTO!。

2 单相流场特性研究

许多学者针对湍流内的液滴破碎的尺寸分布提出了预测模型，这些模型描述的核心是液滴尺寸和湍流特征之间的关系，因此掌握双筒旋转装置内的湍流特征参数是研究液滴分散特性的基础。

2.1 切向速度分析

切向速度梯度反映了流场内离心力的大小，相对离心力（RCF，Relative Centrifugal Force）可以通过切向速度vt计算（RCF=v2tg-1r-1），通过分析其分布规律可以获得流场的旋流强弱。

不同内筒转速（500、1 000、1 500、2 000、2 500、3 000 r/min）下的单侧壁面间隙的切向速度分布如图4所示，Z=0.635 m处为内筒壁面，Z=0.685 m处为外筒壁面。由图4可知，在同一转速下，距离筒壁面约1 mm内，切向速度的变化较为明显，存在大的速度梯度，而距离外筒壁面约4 mm内，切向速度基本保持恒定，可见在内筒壁面附近的大部分区域内切向速度分布均匀；此外切向速度分布呈准自由涡，随半径的增大切向速度减小，液体绕轴线旋转的同时沿轴线移动，呈螺线方式运动。

对于不同转速而言，双筒内壁间隙中的流体所受到的切向速度随内筒转速的增大而增大，且与较小内筒转速的工况相比，在较大内筒转速的工况下，在靠近内筒外壁1 mm区域处有更大的速度梯度。综上，新型双筒旋转装置内的切向速度在绝大部分区域分布均匀，内筒转速越小均匀性越好，在某一转速下在Z轴坐标从0.065 5 m到0.068 5 m的ZX环状截面上可以获得切向速度恒定的旋转湍流场，有利于后续液滴分散特性的研究。

图4 单侧间隙不同内筒转速下的切向速度分布Fig.4 Tangential velocity distribution with different inner cylinder rotating speed in the single gap

2.2 湍流耗散率分析

湍流脉动在谱空间分布呈现不同尺度的分布，大尺度脉动含有湍动能的绝大部分，而小尺度脉动含有较少动能，1922年L.F.Richardson[20]首次提出湍动能输运过程，也称为湍动能的串级过程，主要过程为大尺度脉动不断的向小尺度脉动输出能量，小尺寸脉动把输送来的动能全部耗散掉，流体的惯性将大尺度脉动动能输送给小尺度脉动。湍流耗散率便是这种能量耗散强度的表征，通常用ε表示，是湍流运动中的一个重要参数。根据J.O.Hinze[7]的研究，湍流场中主导油滴破碎的力是动态压力，对于油滴尺寸在惯性子区范围内的湍流场可以认为是各向同性的，故动态压力可以由湍流耗散率ε表示。因此湍流耗散率不仅可以看作湍流强弱的标志，也反映了流场供给液滴破碎的能量大小，通过分析其分布规律可以获得装置内湍流强度大小，并初步预测油滴在同心旋转圆筒装置内的破碎情况。

图5为y=15.5 mm处不同内筒转速下单侧壁面间隙的湍流耗散率ε分布。对于同一转速而言，在靠近内筒壁面约1.5 mm内，湍流耗散率的变化较为明显，其梯度较大，在靠近外筒壁面约3.5 mm内，湍流耗散率ε基本保持一致；对于不同转速而言，双筒内壁间隙中的流体所受到的湍流耗散率ε随内筒转速的增大而增大，且与较小内筒转速的工况相比，在较大内筒转速的工况下，在靠近内筒外壁1.5 mm区域处有更大的变化梯度，且在靠近外壁面的3.5 mm内，内筒转速对ε的数值并没有太大影响。总体看来，新型同心旋转圆筒中内筒附近的湍流强度较大，易造成液滴的破碎，靠近外筒的大部分区域（Z轴坐标从0.065 5 m到0.068 5 m的ZX环状截面）的湍流耗散率分布与切向速度类似，数值基本不变，揭示了此处湍流强度及油滴破碎的概率相同，结合切向速度分布，将Z轴坐标从0.065 5 m到0.068 5 m的ZX环状截面作为后续研究对象。

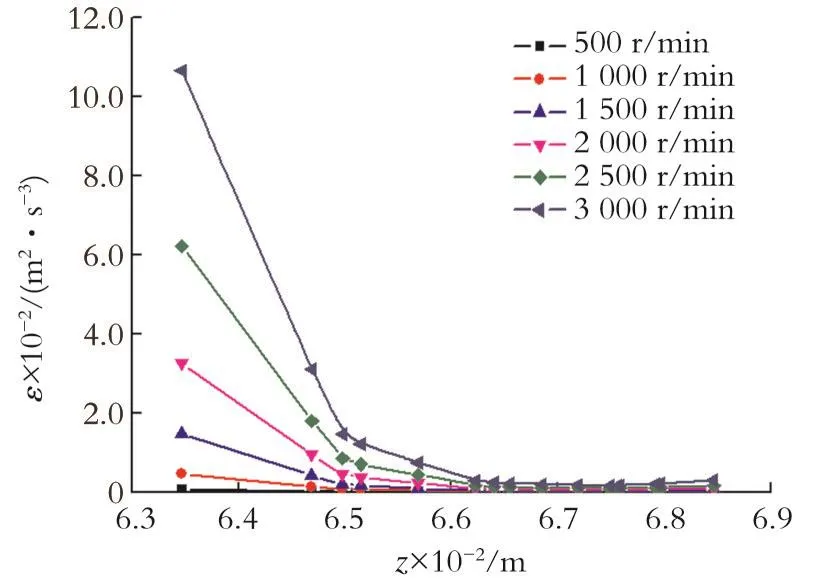
图5 不同内筒转速下单侧间隙湍流耗散率分布Fig.5 Turbulent dissipation rate distribution with different inner cylinder rotating speed in the single gap

3 油滴分散特性研究

3.1 油滴运动轨迹分析

以2 500 r/min为例，油滴在流场中的运动轨迹矢量图如图6所示。

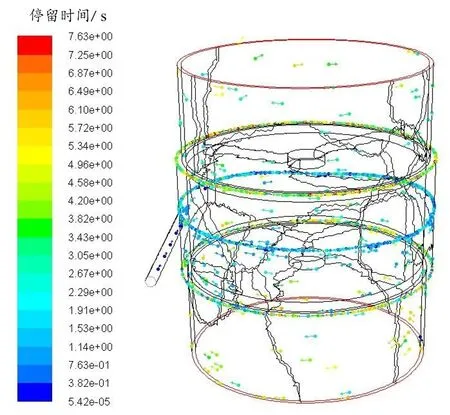
图6 油滴运动轨迹矢量图Fig.6 Vector diagram of oil droplet motion

由图6可知，分散相油滴由入口管进入流场内后，在流场内沿顺时针方向旋转，油滴绕轴线旋转的同时沿轴线移动，呈螺线方式运动。由图6可见，油滴在进入流场后4 s左右油滴从上下两个环形出口流出，这与常用的液液旋流分离器内的停留时间的数量级吻合，说明油滴受旋转湍流场内动态压力的作用时间相同，结合上述旋转湍流场分布特点，进一步验证了本文研究的新型双筒旋转装置可以用于研究旋流器等流体机械的内油滴分散特性。

3.2 油滴粒径分布分析

为了分析内筒转速对液滴破碎的影响，设置入口处的油滴粒径分布符合最大粒径为0.80 mm，最小粒径为0.10 mm，中径为0.35 mm的正态分布。图7为相同流动时间内，内筒转速为500、1 500、2 500 r/min下整个流场中的油滴粒径分布。

由图7可以看出，在相同流动时间内，内筒转速越高，运动到上下两个环形出口的油滴越多。油滴进入流场后，在入口高度处的环状截面内破碎程度较小，经过一段时间的剪切作用后，油滴出现明显的破碎，与Hinze的结论一致，即液滴的破碎过程通常是分阶段进行的，液滴首先发生变形，当韦伯数大于临界韦伯数时，液滴才会发生破碎。当内筒转速为500 r/min时，分散相油滴在流场中能够发生破碎，但流场中的能量并不足以使油滴运动到出口位置，破碎的油滴聚集在入口附近的环形区域中，破碎后油滴的粒径大多集中在0.04～0.08 mm。当内筒转速为1 500 r/min时，破碎后油滴的粒径大多集中在0.002～0.080 mm。当内筒转速为2 500 r/min时，破碎后液滴的粒径集中在0.003～0.040 mm。随着该装置内筒转速的不断提高，经流场剪切发生破碎后的油滴粒径不断减小。

3.3 流场特性与油滴分散特性的关系

液滴在旋转湍流流场中的分散特性不仅与流场作用在液滴表面的动态压力有关，也与流型有关[7]，其决定着液滴的变形类型，这也解释了在不同油水设备（搅拌器、管道、静态混合器等）中液滴的分散特性是不同的，故旋转湍流场中的分散特性值得进一步研究。

如前所述，在湍流场中引起液滴变形甚至破碎的主因是动态压力，而液滴的表面力的作用是抵抗液滴的变形破碎，Kolmogorov-Hinze理论建立的液滴最大稳定粒径半经验公式仅仅考虑了界面张力的影响，而忽略液滴自身黏性力的影响，其表达式如下：

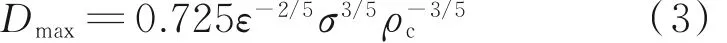
式（3）中，Dmax为液滴最大稳定粒径，m；ε为湍流耗散率，m2/s3；σ为油水界面张力，N/m；ρc为连续相密度，kg/m3。

式（3）只对低黏度分散相适用，随后F.B.Sprow[8]、J.T.Davies[21]和 R.V.Calabrese 等[22]对 式（3）进行了进一步修正。

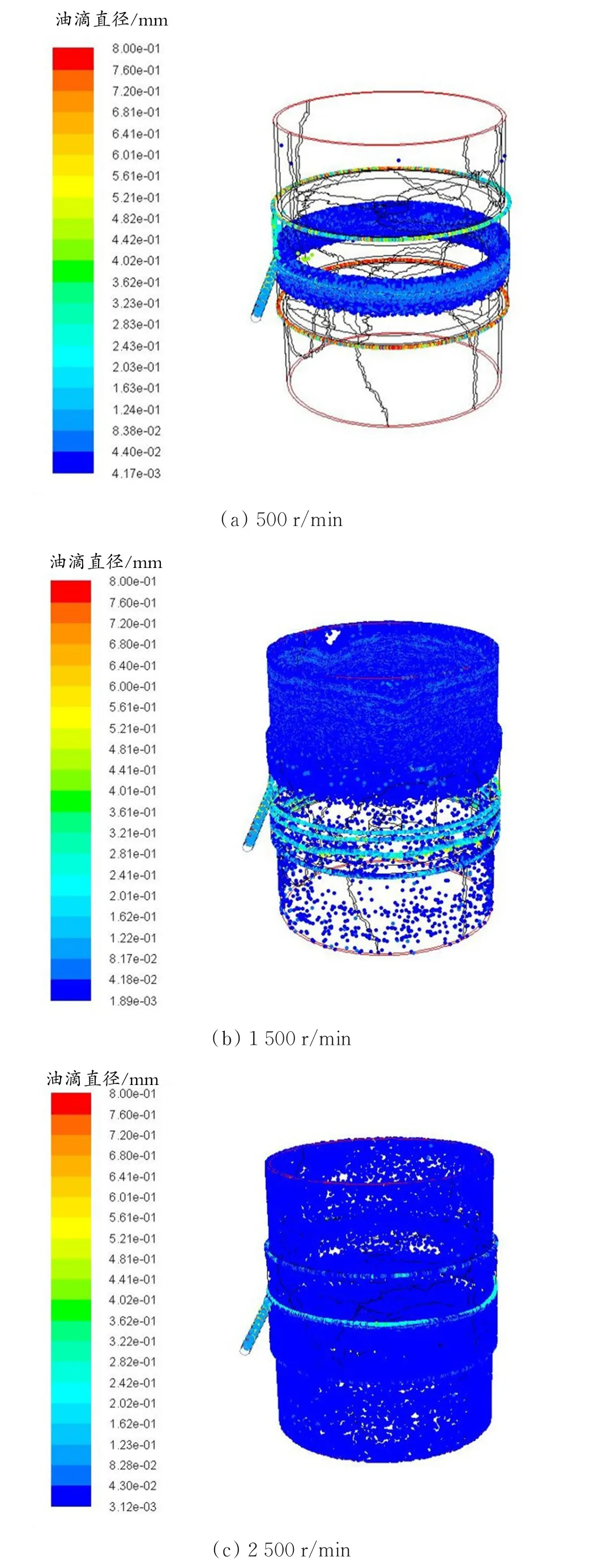
图7 不同转速下流场内油滴粒径分布Fig.7 Oil droplet size distribution at different rotating speeds

其中，J.T.Davies将液滴的黏性力引入受力平衡的分析中，建立了考虑分散相黏性影响的最大稳定粒径半经验公式，表达式如下：

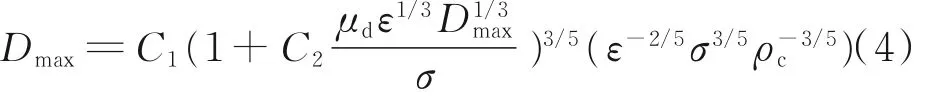
式（4）中，C1、C2为经验常数，需要由实验或模拟进一步确定；μd为分散相的黏度，m2/s。

从式（4）可以看出，当分散相黏度μd很小（趋于0）时，式（4）变为式（3），进一步说明了式（3）适用于分散相黏度较小的条件。同时，E.Pereyra等[23]对Hinze和J.T.Davis的最大稳定粒径的半经验公式与分散相黏度范围较广的实验数据进行对比，研究发现Hinze半经验公式与黏度比（分散相黏度μd与连续相黏度μc之比）小于3的实验数据较吻合，J.T.Davis的半经验公式与黏度比大于3的实验数据较吻合。本文研究油水黏度比为3.31，故采用J.T.Davis的半经验公式为模拟结果进行拟合。

基于新型同心圆筒旋转装置模拟（雷诺数和相对离心力分别在 5.5×104～2.4×105，21.9～643.3），获得从Z=0.065 5 m到Z=0.068 5 m这个环状截面上的质量平均湍流耗散率ε和油滴分散粒径D95（根据 W.Clayton[24]结论，令Dmax≈D95），结合式（4）以因变量对该函数关系式进行拟合，结果如图8所示。

拟合所得的经验关系式的标准差为0.778，具体形式为：

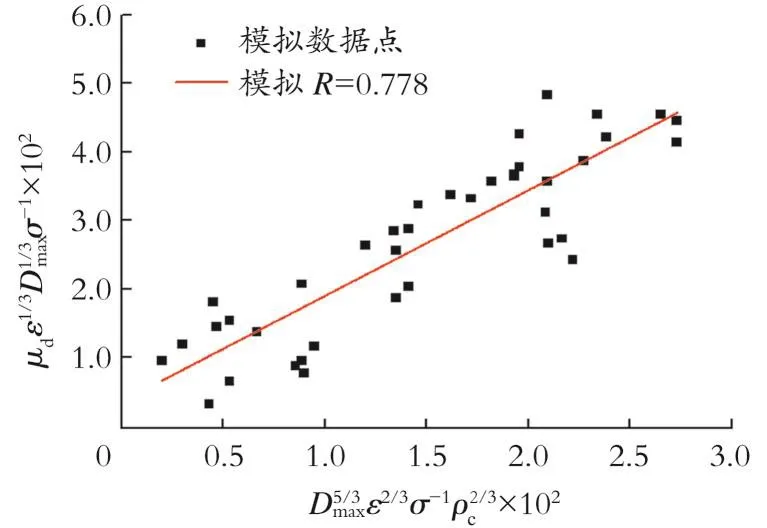
图8 流场特性与油滴分散特性经验关系式的拟合Fig.8 Empirical relationship between flow field characteristics and droplet dispersion characteristics

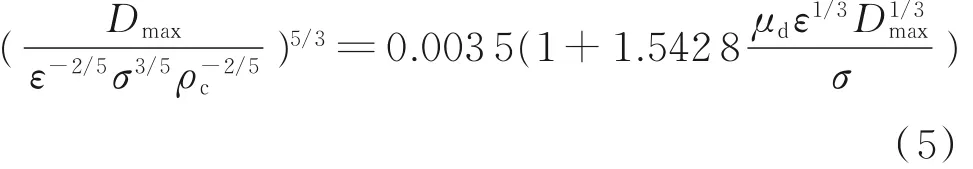
由式（5）可知，油滴最大稳定粒径Dmax的影响因素很多，不仅与其自身的表面张力、黏度、密度有关，还与流场内的湍流耗散率有关，通过式（5）初步建立了流场特性与油滴分散特性的关系，可以计算不同流场条件下油滴的最大稳定粒径，用作初步预测油水分散体系中油滴尺寸，为相关工程设计提供依据。

根据式（5）可以获得最大稳定直径、湍流耗散率与临界韦伯数三者之间的关系，为旋流器内液滴破碎的临界流场条件预测提供合理参考，关系如图9所示。由图9可知，湍流耗散率与临界韦伯数呈对数函数关系，随着湍流耗散率的增大，临界韦伯数先快速增加，后增幅逐渐减缓；且随着最大稳定直径的增加，临界韦伯数的增加速度不变。液滴临界直径越大，临界韦伯数越小，即液滴越易破碎。在本文流场条件下，临界韦伯数在0～7.0变化，是一个与液滴直径、湍流耗散率、油水黏度、界面张力等有关的量。

图9 液滴破碎的临界条件Fig.9 Critical conditions for droplet breakup

3.4 与实验结果对比

在不同的油水物性和流场特性下许多研究者都对式（4）进行拟合，得到了不同的C1、C2的值，具体见表1。

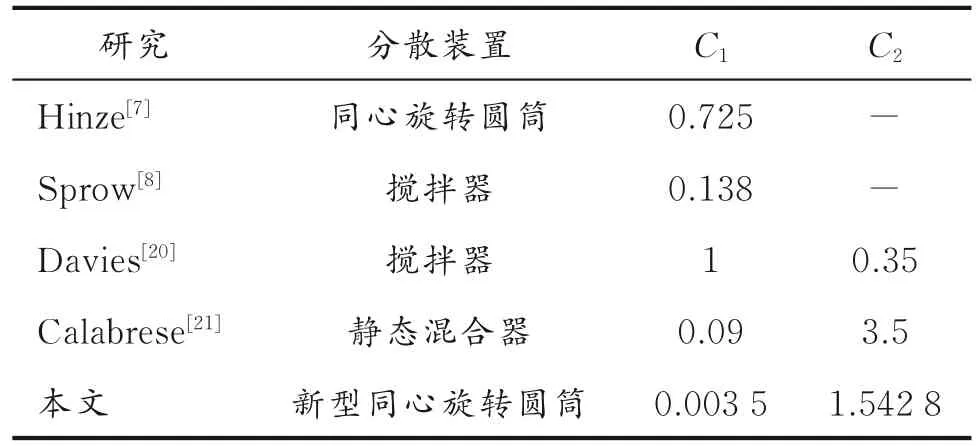
表1 不同条件下经验常数C1、C2的值Table 1 Values of constants C1and C2under different conditions

由表1可知，不同的流场条件和油水物性对油滴的分散特性的影响很大，本文进一步完善了旋转湍流场内油水分散特性的研究。

为了验证最大稳定粒径半经验公式的准确性，采用式（5）预测了R.V.Calabrese[22]实验条件下油滴最大稳定粒径，并与Calabrese的实验结果进行对比，结果如图10所示。

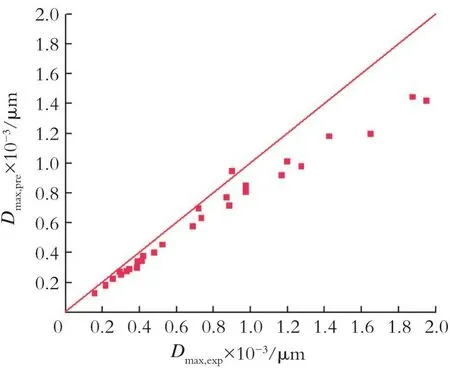
图10 预测的最大稳定粒径与Calabrese实验对比Fig.10 Comparison between current predictions and Calabrese experimental maximum stable particle size.

由图10看出，本文建立的最大稳定粒径的半经验模型与实验数据基本吻合，最大相对误差27.5%，且相对误差在20%以上的数据都集中在Dmax≥750 μm 的大粒径区，对于 Dmax＜ 750 μm 的小粒径区拟合效果较好。这是由于本文研究的湍流较强，其中平均湍流耗散率为0.3～90 m2/s3，而Calabrese研究湍流耗散率为3×10-6～2×10-3m2/s3，故在较强湍流作用下半经验公式较准确；此外，Calabrese实验采用的设备为搅拌器，其内湍流耗散率分布非常不均匀，由于Calabrese文献中没有明确介绍实验条件下的湍流耗散率，本文在采用半经验公式预测最大稳定粒径时采用Rushton的经验公式=0.97N3L2来计算也是产生误差的原因之一。综上，本文建立的半经验公式（5）能够较准确的预测湍流较强、分散相黏度较高时油水分散体系中油滴最大稳定粒径，可作为工程应用于初步估计分散相最大粒径的有效手段。

4 结 论

新型的同心旋转圆筒内液滴运动时间与常用液液旋流器内液滴停留时间数量级吻合，且间隙内绝大部分位置处的流场参数分布均匀，可用于流体机械内旋转湍流场对液液分散体系中分散相尺寸分布的研究。本文采用数值模拟的方法，对高含水条件下新型同心旋转圆筒内油滴所处的流场条件及自身的分散特性展开研究，主要结论如下：

（1）内外筒壁环形间隙内的切向速度场和湍流耗散率从内向外先快速下降再平稳不变，在靠近外筒壁面处二者数值较小且梯度较小，分布较为均匀。

（2）靠近内筒区域中，随着内筒转速的提高，切向速度和湍流耗散率及其梯度随之增加；而在靠近外筒壁面的流场中，内筒旋转速度对切向速度和湍流耗散率基本没有影响。

（3）在Hinze模型的基础上，考虑了油滴黏度对临界韦伯数的影响，初步建立了雷诺数和相对离心力分别在5.5×104～2.4×105，21.9～643.3旋转湍流场中的流场特性与油滴分散特性的经验关系式。