基于CFD方法的无限大平板热扩散数值模拟

王 博，陈一鸣，杜胜男，王卫强

（辽宁石油化工大学石油天然气工程学院，辽宁抚顺113001）

21世纪，随着计算机技术的出现和发展，数值分析逐渐成为和理论分析、实验研究相并列的三大重要科学研究手段之一。数值方法可以对理论分析难以求解的复杂问题进行模拟求解，扩大了研究范围。同时，数值方法可以节约实验所带来的成本，加快科学发展的速度。从方法论的角度，流体流动与传热的描述可以分为宏观、介观和微观三个层次[1]。传统计算流体力学（Computational Fluid Dynamics，CFD）主要从宏观角度出发，建立连续介质模型，将非线性微分方程转换成非线性代数方程组，通过反复迭代进行求解。其中，具有代表性的是有限体积法（Finite volume method，FVM）和有限差分法（Finite Difference Method，FDM）[2]。

N-S方程是从复杂的流体运动中简化出来的一个重要模型，该方程是一个非线性偏微分方程组，运用传统CFD方法求解该方程非常困难，到目前为止，只有极少数非常简单的流动问题才能求其精确解，大多数还是要通过离散方法求其数值解，尤其对于不可压缩流动N-S方程的求解，压力方程具有椭圆形，无法推进求解，收敛性较差，因此传统CFD方法具有一定的局限性。国内学者阎超等[3]、国外学者 H.Charles[4]、F.H.Moukalled等[5]对此进行了详细的分析。为了克服传统CFD方法求解困难及复杂边界难以处理的问题，基于介观层次的格子玻尔兹曼方法（Lattice Boltzmann Method，LBM）应运而生，该方法是将流体离散成流体粒子，物理区域离散成格子，时间变量离散成时间步长，按照简化的动力学模型，求解格线上宏观特征值的平均值，进而求解流场[6]。相比之下，LBM方法具有物理意义清晰、边界处理简单、程序易于实施、模型健壮性高等优点。因此，LBM方法是目前最具前途的数值模拟方法之一，国内学者何雅玲等[7]、郭照立等[8]，国外学者S.Chen等[9]、穆罕默德·阿卜杜勒马吉德[10]对该方法的应用及发展都做出了较为详尽的诠释。李江涛等[11]将LBM方法与FDM方法相结合对页岩气的升尺度渗流进行了模拟；李校等[12]基于LBM理论，运用标准k-ε模型对二维室内湍流空气进行了数值模拟；刘海湖[13]运用LBM-FDM方法对不相溶的两种表面活性剂混合问题进行了数值模拟，对混合后的表面张力做出了详细的分析。

通过上述分析可知，LBM方法对于求解流体流动与传热等物理问题表现出较强的适用性，但目前对LBM方法的研究主要以应用技术为主，并且众多研究是将该方法与传统的CFD方法相结合，而对LBM方法与传统CFD方法相异之处的对比研究却鲜有报道。因此，为了对比分析传统CFD方法与LBM方法的差异，以无限大平板热扩散问题为例，运用3种数值模拟方法对平板间的温度分布进行研究，并将LBM方法的求解结果与FDM方法和FEA方法的求解结果进行对比，进而从直观角度明确LBM方法的计算可行性及优越性。

1 物理模型

1.1 问题描述

假设平板初始温度T=0℃，当时间t≥0时，平板左侧施加高温T≈100℃，平板长度L=100 m，平板厚度相较于平板长度极小，可忽略不计。平板几何模型如图1所示。

1.2 扩散方程

由于平板厚度远小于平板长度，且平板理论上为无限大平板。因此，可将平板间的热扩散问题看成一维热扩散问题。一维热扩散方程可以表示为：

式中，T为温度，℃；ρ为介质的密度，kg/m3；c为比热容，J/(kg⋅℃)；k为热传导系数，W/(m⋅℃)；α为热扩散系数，取 0.25[14]。

图1 平板几何模型Fig.1 Flat geometry model

2 数值方法

2.1 有限差分法

2.1.1 基本思路 FDM方法的基本思想是把连续的定解区域用有限个离散点所构成的网格来代替，离散点称作网格节点；用网格节点上定义的离散变量函数近似代替连续定解变量的函数，用有限差分方程组代替原微分代数方程组，用离散差商解近似代替连续微商解，然后再利用插值方法将离散解还原为计算域的近似解[15]。

FDM方法的求解步骤为：（1）区域离散化，即将偏微分方程的求解区域细分成由有限个格点组成的网格。（2）近似替代，即用有限差分计算值替代每一个格点的导数值。（3）逼近求解，即用一个插值多项式及其微分来代替原偏微分方程进行求解。

2.1.2 区域离散化 针对求解区域离散化的节点个数及节点间距没有固定的要求，为了增加求解效率，对计算域进行均匀离散化处理，结果如图2所示。

图2 离散化节点分布Fig.2 Discretized node distribution

2.1.3 近似替代 按照不同的划分标准，有限差分的近似方法可分为：（1）按照差分精度可分为一阶格式、二阶格式和高阶格式。（2）按照差分的空间形式可分为中心格式和逆风格式。（3）按照时间因子的影响可分为显格式、隐格式、显隐交替格式等。针对平板间的热扩散问题，选择显式有限差分方法，具体形式为：

时间导数采用一阶前向差分，即

空间导数采用二阶中心差分，即

式中，β为相关系数，取 0.01；Δx为步长；Δt为时间间隔。

因此，节点i处的扩散方程可进一步表示为：

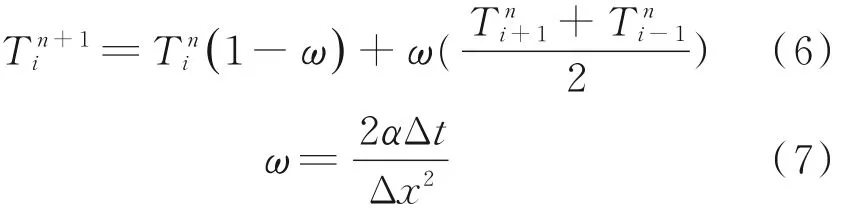
式中，ω为松弛频率；α为扩散系数，m2/s；t为时间，s。

2.2 格子玻尔兹曼法

2.2.1 基本思路 LBM方法是一种基于介观尺度的计算流体力学方法。该方法相比于传统模拟方法，具有介于微观分子动力学模型和宏观连续模型的介观模型特点。因此，该方法具备流体相互作用描述简单、复杂边界易于设置、易于并行计算、程序易于实施等优势[16]。玻尔兹曼理论及LBM方法已经广泛地被认为是描述流体运动与处理工程问题的有效手段。LBM方法的求解流程如图3所示。2.2.2 求解设置 针对恒温无限大平板的热扩散问题，基于LBM理论，选用D2Q4模型，平板轴向划分100个格子区间，平板左侧端面初始化温度为100℃，热扩散系数α为 0.25。图 4、5为二维（D2Q4）格子排布及热扩散格子分布示意。

根据Mohamad提出的，温度分布函数的动力学方程可写成[17]：

式中，ck为格子运动速度，m/s；Ωk为碰撞算子，根据BGK近似求解，即

式中，τ为达到平衡态分布函数的松弛时间，s；Teqk为

平衡态分布函数，定义式如下：

式中，Tk(x,t)为温度分布函数；wk为k方向权重因子。

采用BGK近似后，温度分布函数离散化表达式为：

图3 LBM方法求解流程Fig.3 LBM method solution flow chart

图4 一维格子排布示意Fig.4 Schematic diagram of one-dimensional grid arrangement

图5 一维热扩散格子分布示意Fig.5 Schematic diagram of one-dimensional thermal diffusion lattice distribution

将式（10）代入式（11）化简得一维空间扩散方程为：

2.3 有限体积法

2.3.1 基本思路 FVM方法作为目前CFD领域最成熟的算法。该算法是将流体的Euler控制方程在单元控制体内进行积分后离散求解[18]。就离散方法而言，有限体积法可视作有限单元法和有限差分法的中间物。该方法求解流程如图6所示。

图6 FVM法求解流程Fig.6 FVM method solution flow chart

目前常用的CFD软件，例如Fluent、CFX等都是基于该方法。因此，采用Fluent作为FVM方法的代表对平板间的热扩散问题进行求解。恒温无限大平板的上、下壁面为绝热边界，因此平板法向方向无温度变化现象，由于计算域内介质的温度仅一个方向有变化且传热系数不变，每一个物质元流入与流出的热量均相等，平板间温度的变化情况与模型的维度无关，可将计算域简化为一维温度场，为了更好地展现流场细节，利用FVM方法对问题进行求解时，以三维的模型进行展示。

2.3.2 网格划分 采用结构化网格对平板进行网格划分，平板长度远远大于宽度且计算域为规则对称区域，因此选取平板上截面的二维模型进行模拟分析，网格具体划分如图7所示。

图7 网格划分Fig.7 Mesh generation

2.3.3 边界条件 平板左侧端面设定初始温度为100℃，右侧端面无限延展，较远端面处设置为0℃，上下设置为壁面；计算域材料的扩散系数为0.25。

3 结果分析

3.1 FDM方法结果分析

基于FDM方法，运用Fortran编译器进行程序编写，设置空间域离散节点之间的距离Δx=1.0，时间域离散步长Δt=0.5，轴线方向离散格子数为100，平板左侧端面初始化温度为1℃，平板间介质的热扩散系数α=0.25，通过归一化求解[19]可得时间步数为400，求解得平板间温度变化情况如图8所示。

由图8可知，FDM方法求解得到的平板间温度变化呈现递减的趋势，且变化曲线近似服从对数分布函数，即温度递减的速率在逐渐降低；恒温条件下，平板左侧端面温度取最大值，沿着轴线方向温度逐渐减小，轴向20 m附近温度降至0℃附近，30 m后至无穷远处温度始终保持在0℃。

3.2 LBM方法结果分析

基于LBM方法，运用Fortran编译器进行程序编写，沿平板轴线方向均匀划分100个离散格子，设置时间步长Δt=1.0，格子间距Δx=1.0，平板左侧端面初始化温度为100℃，平板间介质的热扩散系数α=0.25，计算当t=200 s时，平板间的温度分布情况，结果如图9所示。由图9可知，LBM方法求解得到的平板间温度变化规律与FDM方法求解的结果近似相同，两种方法下的温度变化曲线吻合度较高。

图9 基于LBM方法的温度变化Fig.9 Temperature change based on LBM method

为了验证两种求解方法得到的温度变化分布情况，选取轴向变动数据进行拟合处理，结果如图10所示。由图10可知，LBM方法与FDM方法求解得到的平板间温度变化曲线近似服从对数分布，其拟合曲线为y=-35.89lnx+117.47，曲线拟合优度R2为96.79%。

图10 温度变化拟合Fig.10 Temperature change fitting

3.3 FVM方法结果分析

针对恒温条件下的平板间热扩散问题，运用Ansys Workbench中稳态热分析模型对其进行求解，由于平板轴线方向尺寸为无限大，平板厚度及宽度远远小于其长度，可选取平板上表面作为分析系统的代表计算域；计算域左侧边界设置高温T=100℃，平板间介质的热扩散系数α=0.25，求解得平板间温度变化情况如图11所示。

图11 温度云图Fig.11 Temperature cloud map

由图11可知，基于FVM方法得到的平板间温度变化云图沿轴线方向逐渐减小，且温度条带近似均匀分布；平板左侧端面温度取最大值，平板右侧区域温度逐渐降低至0℃，即平板无限远处温度降到最低；为直观地分析温度沿轴线方向的变化规律，绘制温度变化曲线如图12所示。由图12可知，FVM方法求解得到的平板间温度呈减小的趋势，且减小的速率基本保持不变，即平板间的温度变化曲线近似呈现线性分布，该结论与上述两种方法相比略有差异。

3.4 对比分析

图13为3种求解方法得到的温度变化。由图13可知，3种数值方法皆可以很好地模拟恒温边界条件下的热扩散问题，且平板间的温度变化皆呈减小的趋势；根据温度变化曲线的切线变化率可知，LBM方法和FDM方法的温度变化曲线表现非线性趋势，且温度变化情况较为相近。相比之下，FVM方法求解结果表现出较大的差异，其温度变化曲线近似线性趋势；根据热扩散理论[20-21]可知，介质热扩散速度与温度呈正比例变化，即温度越高，分子无规则运动越剧烈，分子间碰撞频率及强度会加大，单个分子动能增加，最终会导致平板间的分子总动能增加；由LBM方法及FDM方法的求解结果可知，平板左侧端面温度达到最大值，因此扩散初期速度较快，即温度变化曲线切线斜率达到最大值，随着温度的逐渐降低，平板间热扩散速度逐渐减小，即温度曲线切线斜率越来越小；通过对比可知，针对恒温条件的热扩散问题，LBM方法和FDM方法求解得到的温度变化曲线热扩散速度在逐渐减小，符合热扩散机理，而FVM方法求解得到的温度变化曲线热扩散速度保持不变，说明该方法对于热扩散的求解是可行的，但是求解精度要低于另外两种方法。

图12 基于FVM方法的温度变化Fig.12 Temperature change based on FVM method

图13 平板轴向温度变化Fig.13 Plate axial temperature curve

4 结 论

针对无限大平板的热扩散问题，运用3种CFD方法对温度分布进行了求解并得到：

（1）相同物理模型条件下，针对恒温热边界条件下的热扩散问题，LBM方法和FDM方法的求解准确性要略优于FVM方法。

（2）运用归一化和尺度准则，计算相同条件下的热扩散问题，FDM的求解步数要大于LBM方法，即针对扩散问题，LBM方法求解时间比较短，计算效率较高。

（3）基于LBM方法的一维热扩散问题，该方法具有较好的准确性和适用性，为后期研究二维、三维的热扩散问题提供了一定的参考价值。