基于OP-FTIR多光路同步监测的VOCs排放量核算研究*

李 波

(中国石化青岛安全工程研究院，山东青岛 266071)

0 前言

挥发性有机物(VOCs)是大气环境污染的重要来源之一，包括非甲烷烃类、含氧有机物、含氯有机物、含氮有机物、含硫有机物等，是形成臭氧和细颗粒物污染的重要前体物[1-2]。2017年，国家环保部为全面加强VOCs污染防治工作，制定了《“十三五”挥发性有机物污染防治工作方案》，明确要求全面提升VOCs环保监管能力，加强VOCs减排核查核算。同年，国家生态环境部颁布《中华人民共和国环境保护税法》，并于2018年1月1日起，按照大气污染物排放量折合的污染当量数开征环境保护税。

VOCs排放量核算作为污染防治减排核查与环境保护税法落地实施的前提，是挥发性有机物治理领域的重要研究内容。当前，针对VOCs排放常用的方法包括实测法、物料衡算法、排放系数法等。实测法更适用于设有VOCs末端治理设施的排放源，但由于石化装置/罐区无组织排放的普遍存在，使得该方法的准确性和适用性受到一定限制；物料衡算法需要详细的工艺、物料等信息，实际数据和参数获取困难，特别是针对发生生化反应的单元，核算结果难以保证；排放系数法是一种半经验半理论的计算方法，易受主观因素影响，同时排放因子等关键数值大多来自于欧美国家，对我国石化行业并不完全适用[3-5]。

随着开路式傅里叶变换红外光谱技术(OP-FTIR)的快速发展，以及其在气态污染物组分定量识别的推广使用，研究人员逐步探索该遥测技术在石化企业VOCs排放核算中的应用。王国龙等[6]建立了一种基于开路式红外光谱仪实测技术的石化企业罐区/污水处理单元源强反算方法；朱亮等[7-8]利用OP-FTIR技术，依托箱体模型(也称质量通量模式)，针对无组织排放普遍存在的炼油装置区/罐区等完成了VOCs排放量核算。本研究以箱体模型为基本原理，以OP-FTIR技术为实测手段，通过合理设定多光路同步监测方案，给出了一种基于面域重构技术的VOCs排放量核算方法，并于华东地区某油库原油储罐实测应用。

1 基于箱体模型的VOCs排放量核算办法

箱体模型是OP-FTIR遥测核算VOCs排放量的一种基础模型，如图1所示，沿风向方向在排放源周围构建封闭箱体，忽略箱体侧壁流入、流出及排放源装置自身沉积等因素影响，可认为在风力推动下污染物均由上风向截面流入、由下风向截面留出，且流出量Qdown与流入量Qup以及箱体内排放源排放量Q间存在关系：Q=Qdown-Qup。

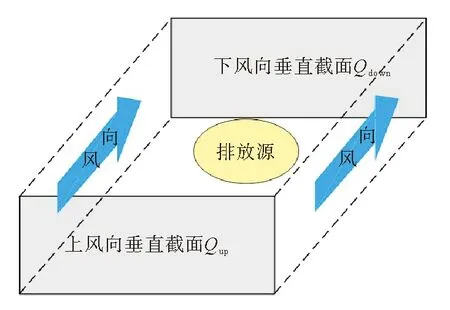
图1 箱体模型示意

针对流出量Qdown与流入量Qup，建立如下方程，即：

Q=Qdown-Qup

=(Csdown·vdown·sinθdown-Csup·vup·sinθup)·t

(1)

式中：Csup、Csdown——上、下风向截面的VOCs面浓度，μmol/mol；

vup·sinθup——上风向截面位置处的风速垂直分量，m/s；

vdown·sinθdown——下风向截面位置处的风速垂直分量，m/s；

t——排放时间，s。

已知，风速大小v及风向角度θ均为可直接测量参数，排放时间t为设定参数，在工艺稳定情况下，可设定为月排放量、年排放量等，结合公式(1)即可明确基于OP-FTIR的VOCs排放量核算研究关键在于上、下风向截面挥发性有机物面浓度Cs的计算问题。为准确计算面浓度，关键在于监测光路如何布设以及面浓度如何核算。2017年贾润中等[9]针对某300 m×422 m炼化装置区，利用主动式红外遥测设备于装置区南北两侧(主导风向为南风)分别设置1条300 m长监测路径，每监测周期(2 min)记录一组，令面浓度Cs=L·H·C，其中L、H分别为监测截面的长和高，即得监测截面面积，C为监测光路上的污染物平均浓度；2020年朱亮等[7-8]针对某独立罐区(包含4个储罐)设置7条独立监测光路(罐区周界4条、罐区内部3条，主导风向东风)，同样采用Cs=L·H·C公式，其中L、H分别为罐区东西长度和储罐高度，C为罐区内部及周界多条监测光路上的污染物平均浓度。上述研究采用了单光路或多光路独立布设的监测方案，各监测截面仅一条光路，光路设计相对简单、随机性大，难以全面准确获取整个截面的污染物浓度信息，且面浓度核算方式相对粗糙，以红外监测所得的线平均浓度近似替代面平均浓度，难以准确核算监测截面VOCs浓度数值。

鉴于此，结合OP-FTIR线式检测技术，针对上下风向监测截面面浓度的准确计算问题，笔者给出如下办法：首先，利用OP-FTIR在线监测设备，设计多光路同步监测的优化布局方案，便于尽可能多地获取截面污染物浓度数据；其次，基于OP-FTIR多光路实测数据，利用面域重构算法建立截面污染物分布模型，经积分运算得到面浓度；最后将面浓度带入公式(1)实现VOCs排放量的准确核算。

2 基于OP-FTIR的多光路同步监测方案

2.1 开路式傅里叶变换红外光谱技术

开路式傅里叶变换红外光谱技术(简称OP-FTIR)，是一种定量识别气体组分的线式检测技术，与传统点式检测手段相比可实现连续在线长光路监测，响应速度快，灵敏度高，检测范围广，检测结果更具代表性[10-11]。具体检测系统如图2所示，由主动式OP-FTIR设备、立方反光镜组成，主动式OP-FTIR设备发射红外光束经气体云吸收后，由立方反射镜沿原光路反射回OP-FTIR设备，经傅里叶变换等解析后定量识别气体云组分及浓度信息。

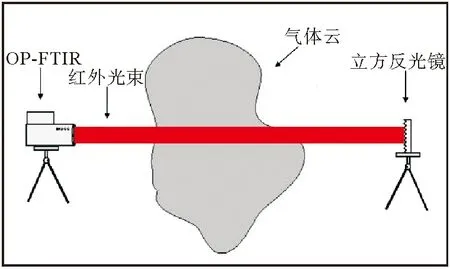
图2 OP-FTIR检测系统

2.2 VRPM监测方式

VRPM(Vertical Radial Plume Mapping，垂直截面径向羽流式监测方法)是美国OTM10ORS标准提供的一种基于线式光路的垂直截面气体检测方法[12]，具体监测方式如图3所示，矩形区域为垂直监测截面，OA、OB、OC为下、中、上3条监测光路，O为截面内某一近地端点用于放置主动式OP-FTIR设备，A、B、C为红外监测光路另一端点用于放置立体反光镜，B为垂直边线AC的近似中点。

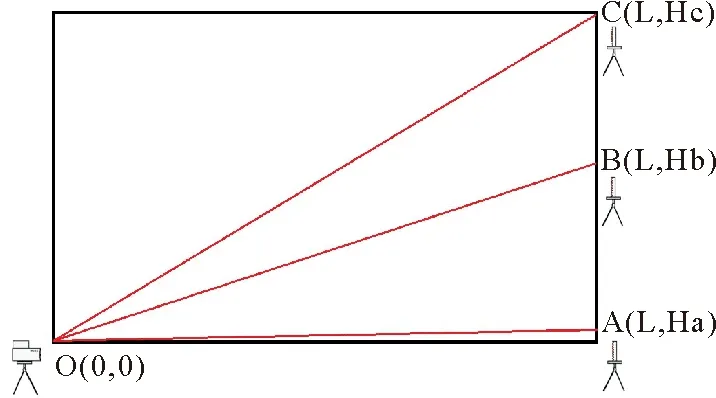
图3 垂直截面内VOCs浓度数据

根据美国OTM10ORS标准，VRPM要求同时进行OA、OB、OC 3条光路监测，用以表征同一时刻内垂直截面的VOCs浓度特征。受制于仪器设备数量的限制，一台OP-FTIR设备同一时刻仅可测量一条光路，为此采用OA、OB、OC 3条光路循环扫描的监测方式，近似获取同一时刻监测截面的VOCs浓度特征。该基于OP-FTIR的多光路同步监测方案，可获取截面内多条光路、同时刻的VOCs浓度，为后续面浓度及排放量核算提供更为全面的数据支撑。

3 基平滑基函数最小化法与多阶二维高斯模型的面域重构技术

3.1 平滑基函数最小化法

针对监测截面面浓度计算的问题，现有研究中多以OP-FTIR光路平均浓度作为面平均浓度，为进一步提高面浓度计算的准确性，引入面域重构技术。平滑基函数最小化法(简称SBFM)作为重要的面域重构算法之一，与迭代算法、多项式拟合等算法有较大不同，该算法首先要建立一个含有未知参数的分布模型用以描述气体浓度的空间分布，并根据采样光路积分浓度或采样点浓度数据，利用误差最小优化算法，解析分布模型的未知参数的最优解，进而实现气体浓度分布模型重构[13-14]。由于SBFM算法以含参分布模型为重构对象，而非面域内各像素点，因而不需要过度复杂、交叉布局的检测光路，可有效降低设备成本和人工成本，更适用于周边环境复杂的现场检测作业。

误差最小优化算法，即以误差函数最小为评判原则，寻找分布模型的最优化参数，通常以平方差之和为误差函数SSE，结合基于OP-FTIR核算排放量的具体需求，定义表达式如下：

(2)

式中：PICpredicted,i——基于含参分布模型计算所得的光路积分浓度，(μmol/mol)·m；

PICobserverd,i——基于OP-FTIR实测所得的光路积分浓度，(μmol/mol)·m；

n——截面内的监测光路数量，无量纲。

3.2 二维高斯分布模型

结合SBFM算法要求，还需定义适用于描述石化企业生产装置/罐区上、下风向截面污染物浓度分布特征的函数模型。已知，二维高斯分布函数是一种重要的二维空间分布函数，常用于描述气态污染物在二维空间内的浓度分布特性[13,15]，其表达式如下：

(3)

式中：x,y——二维平面横、纵坐标，m；

A——浓度权值系数，无量纲；

ρ——峰值位置的光路对笛卡尔坐标系下的角度，弧度；

μ1,μ2——直角坐标系下峰值位置，m；

σ1,σ2——峰位置的标准偏差，无量纲。

由于单阶二维高斯分布函数仅具备单个浓度峰，即难以描述复杂截面的浓度分布特征，因而选用多阶二维高斯分布函数作为垂直截面VOCs浓度分布模型更为合理。在阶次选择上，阶次越高所能描述的分布特征越复杂，参数模型的适用性也越广泛；但随着阶次的增加，参数模型的待拟合参数数量也越多，针对二维高斯分布模型，每增加一个阶次随之增加6个待拟合参数，即在样本数量相同的情况下，参数拟合的难度以及拟合结果的准确性也会随之降低。笔者综合考虑两方面的影响，选用三阶二维高斯分布函数作为监测截面的分布模型。定义三阶二维高斯分布模型为G，则其表达式为：

G=g1(x,y,A1,ρ1,μ1,μ2,σ1,σ2)

+g2(x,y,A2,ρ2,μ3,μ4,σ3,σ4)

+g3(x,y,A3,ρ3,μ5,μ6,σ5,σ6)

(4)

与公式(3)相同，x,y为三阶二维高斯分布参数模型G的横纵坐标轴自变量，未知参数A1,ρ1,μ1,μ2,σ1,σ2,A2,ρ2,μ3,μ4,σ3,σ4,A3,ρ3,μ5,μ6,σ5,σ6为待优化量，根据模型表达式可知，模型G的分布特性有且仅与18个未知参数相关，且该18个未知参数的取值也直接影响模型G对监测截面VOCs分布特性描述的准确性。

为验证三阶二维高斯模型G作为分布模型的适用性，做如下模拟实验。

a) 定义长125 m、宽23.3 m的矩形，用以模拟监测截面；定义矩形内3条线段(0,0)→(125,5.6)、(0,0)→(125,14.6)、(0,0)→(125,23.3)，用以模拟监测截面内3条红外光路。

b) 由于实际截面内污染分布状态以及面浓度为不可知量，考虑到现场实际污染物分布情况复杂多变，因而定义8种不同的空间分布函数，用以代替实际截面的污染物浓度分布状况，即均匀分布函数(常函数)、一阶二维高斯函数、二阶二维高斯函数，直至七阶二维高斯函数；令横纵坐标取值范围为[0,125]、[0,23.3]，其余参数随机设定。

c) 基于已定义的8种空间分布函数，分别计算3条光路(0,0)→(125,5.6)、(0,0)→(125,14.6)、(0,0)→(125,23.3)上的线积分浓度，作为红外实际监测浓度，分别计算矩形区域内的面积分浓度，作为监测截面的实际面浓度。

d) 最后，基于3条红外光路监测浓度，以SBFM为重构算法，以三阶二维高斯函数为含参分布模型，对监测截面进行10次重构试验并计算重构所得面浓度，以及重构所得面浓度与实际面浓度之间的误差。

如图4所示，误差绝对值以散点图表示，平均误差绝对值以点线图表示。

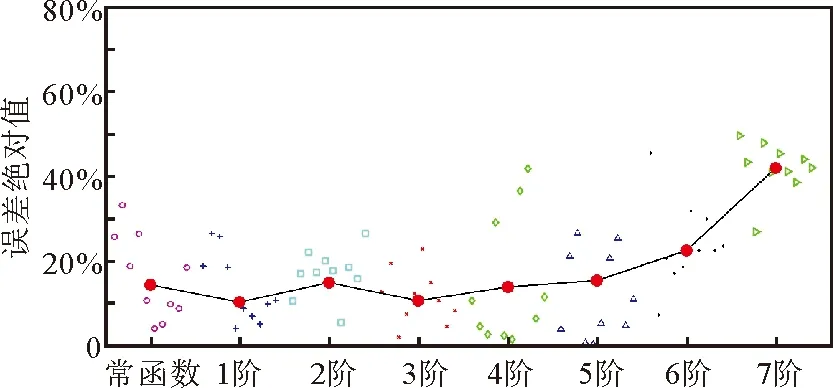
图4 适用性试验面浓度重构误差

由图4可知，分布模型G对五阶及五阶以下高斯分布函数有着较好的重构特性，面浓度重构误差小于16%，随着被重构对象阶次的提高，被重构对象所包含的分布特征越复杂，重构效果也逐渐变差。且经试验验证，分布模型G对三阶高斯分布函数的重构效果最好，同时可有效定位面域的峰值大小和出现位置，峰值浓度重构平均误差为14.91%，峰值位置横、纵坐标重构误差分别为16.98%、5.084%，面浓度重构平均误差为10.55%。

4 某原油储罐VOCs排放监测与核算

4.1 现场检测

2018年4月对华东地区某罐区原油储罐开展监测。原油储罐VOCs泄漏以无组织泄漏为主，常见的泄漏部件包括一二次密封圈泄漏、人孔泄漏、呼吸阀泄漏等，属于典型的无组织面源排放。查阅该地区近年气象数据得知，4-5月份以南风和北风为主，根据模型要求，监测截面需设置于待测目标的上下风向处，结合储罐周边地形特征及消防通道要求，布设方案俯视图如图5所示，A#、B#为相邻的两个原油储罐，A#为待核算储罐，于储罐A#南、北两侧布设①——②和③——④两处监测截面，其中①和③位置放置红外设备，②和④位置放置反光镜。

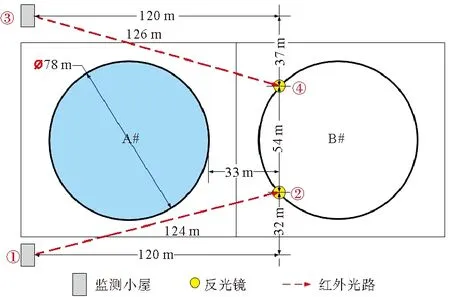
图5 南北侧监测方案平面示意

图6、图7分别为南侧监测截面(也即①——②)和北侧监测截面(也即③——④)内的3条光路布设示意图，O为红外设备安装位置，A、B、C为3面反光镜的固定位置。

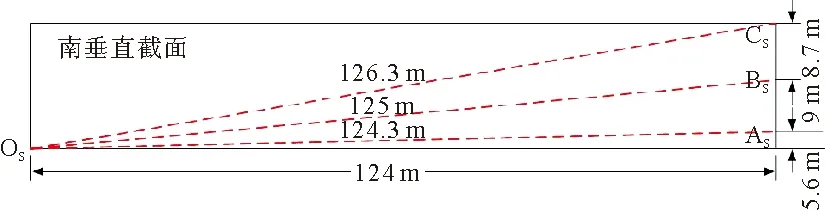
图6 南侧垂直截面示意

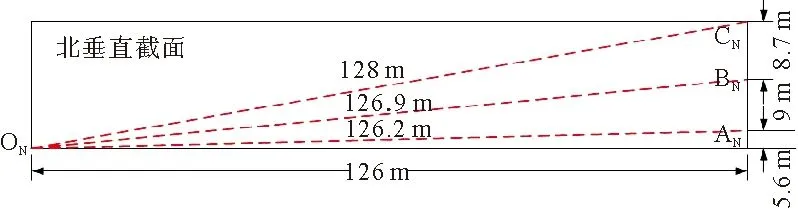
图7 北侧垂直截面示意

现场检测实际场景如图8，主动式OP-FTIR设备放置于检测小屋内，立体反光镜固定于B#罐侧壁，且同侧3面立体反光镜处于同一垂直线。

图8 现场监测

监测方式设定为下、中、上3条光路循环监测，程序设定每条光路采样时间为2 min，考虑到设备定点移动及稳定所需时间，平均每监测周期所需时长为6 min 40 s。

4.2 上、下风向截面重构

考虑到监测过程中，天气、风向、光强减弱、光路遮挡、参数修正等因素的影响，制订如下数据筛选原则：①雨天或雾天条件下的检测数据，删除；②仪器非正常状态下的检测数据，删除；③存在遮挡光路现象的检测数据，删除；④红外光强信号过小的检测数据，删除；⑤施工、消防、烟尘等对吸收光谱产生明显影响条件下的检测数据，删除；⑥实时风向不属于北偏西10°至北偏东10°或南偏西10°至南偏东10°之间的检测数据，删除。

表1所示为2组典型检测样本，样本组1、样本组2分别为南风条件下A罐北侧、南侧监测截面内的VOCs浓度检测样本，每组样本均包含上、中、下3条光路上的VOCs实测光路积分浓度以及光路坐标等信息，各光路起始点坐标均为(0,0)表中不再赘述。

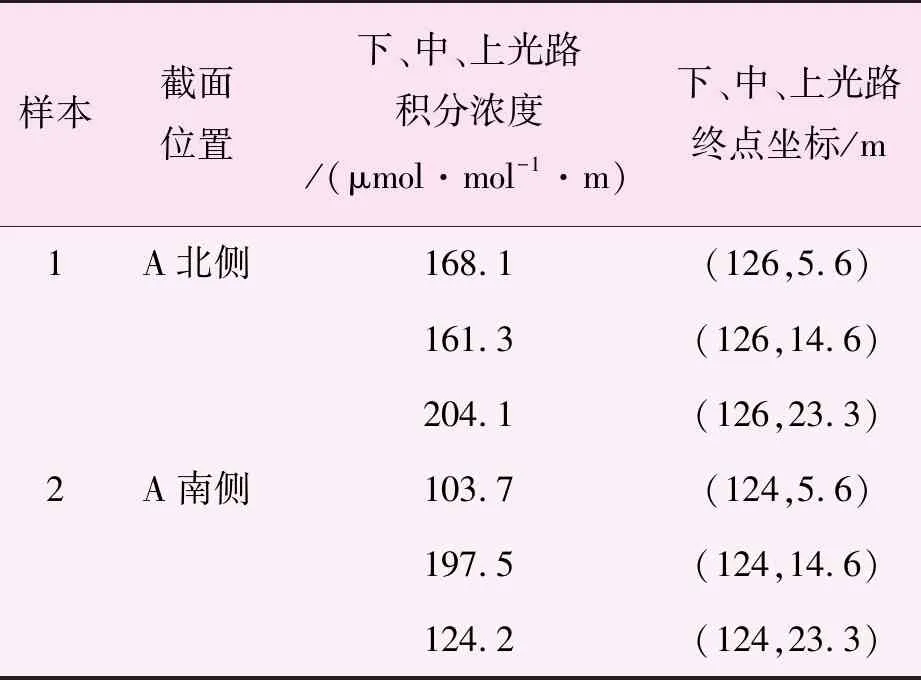
表1 南风条件下两组检测样本

根据实际采样数据，针对样品1、样品2进行多次重构处理并选取误差函数值较小的2个典型重构结果，即样品1-1、样品1-2、样品2-1、样品2-2，重构所得分布模型最优参数值、垂直截面峰值浓度以及垂直截面面浓度如表2所示。

根据表2可以看出，针对同一样本重构所得最优化参数值差别较大，即重构出的三阶二维分布模型并不相同；原因有三：①采样光路数量偏少、难以详细捕捉截面的分布特征信息；②重构算法本身存在的不确定性，在误差最小优化算法方面选用了模拟退火法，该方法有一定概率跳出局部最优，但仍有陷于局部最优的可能；③三阶分布模型含有18个待拟合参量，最优化结果复杂多样。但通过面浓度的重构结果可以看出，在误差函数较小时，针对同一样本重构所得面浓度结果稳定，数值变动不大，该结论已通过多次试验得到证实。

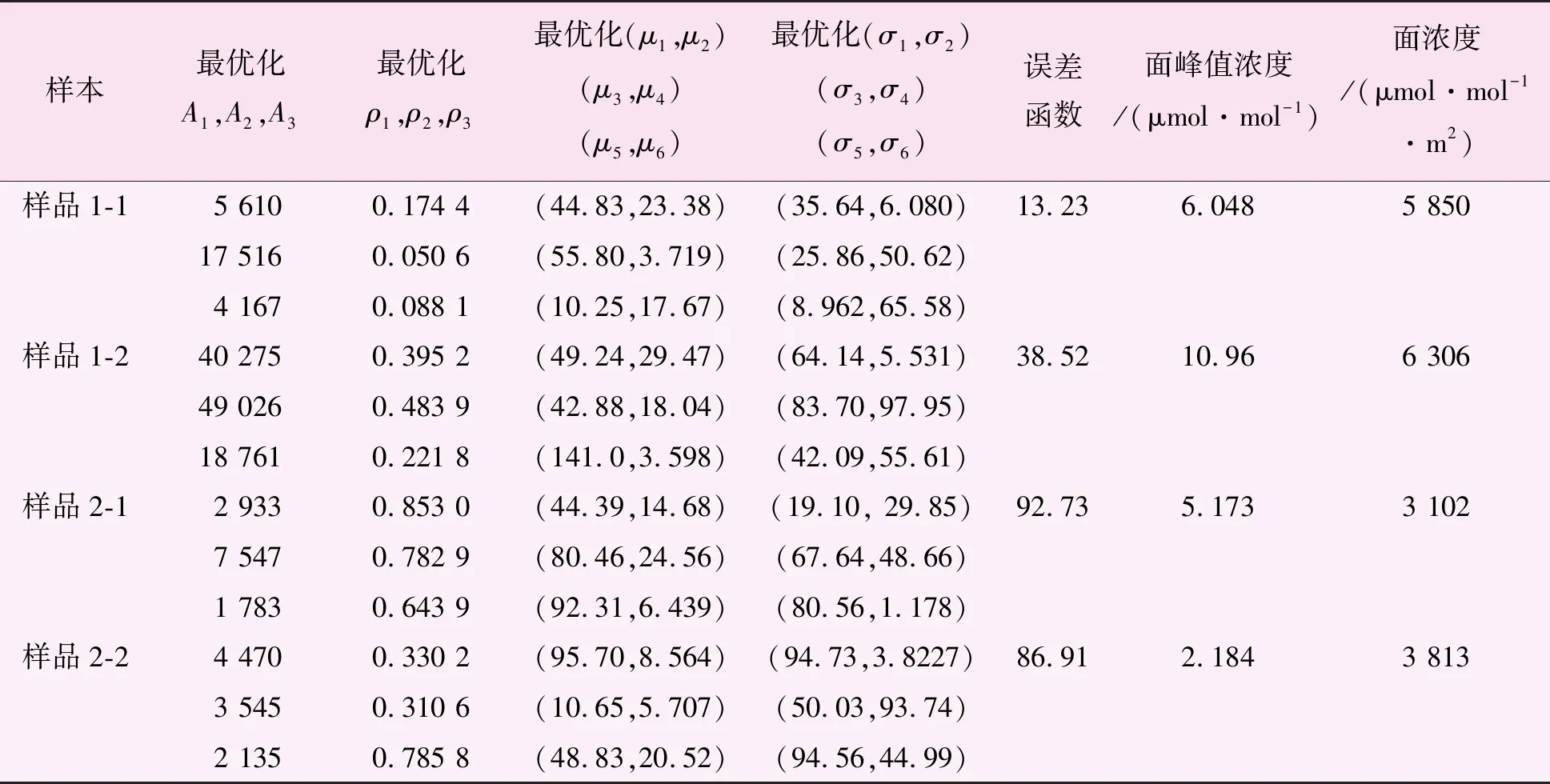
表2 垂直截面重构结果

4.3 基于箱体模型的VOCs排放量核算

首先，根据检测时间上午(9-11时)、中午(11-14时)、下午(14-17时)各筛选5组正南风向检测数据，合计15组；然后，利用面重构技术对15组检测数据进行多次重构分析，筛选重构误差不大于500、重构面域峰值浓度不大于25 μmol/mol的重构结果为有效重构并计算面浓度，针对每组检测数据，进行8次有效重构并得到8次面浓度。各组检测数据重构所得面浓度结果如图9所示，横坐标为各组检测数据，本图仅给出前6组，纵坐标为重构所得监测截面面浓度，图中蓝色实心圆为8次上风向截面面浓度的平均值，红色三角为8次下风向截面面浓度的平均值。

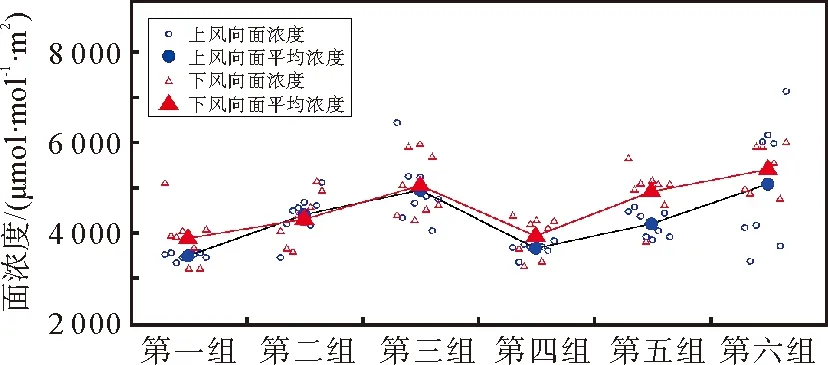
图9 垂直截面面浓度重构结果

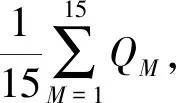
5 结论

a) 利用开路式傅里叶变换红外光谱技术，提供了一种多光路同步监测方案，相较于单光路和多条独立光路监测方式，更有利于获取截面VOCs浓度分布特征，考虑到石化装置无组织泄漏点分布密集以及扩散路径难以预测的特点，该监测方案更具有适用性。另外，理论状态下最高点反光镜的安装高度应不低于待测区域内的最高可能泄漏点的高度。

b) 利用平滑基函数最小化法，结合三阶二维高斯分布模型，实现了截面VOCs分布模型的重构，试验表明：多次重构所得分布模型的最优化参数差异性较大，但所得面浓度结果较为稳定。根据8种分布模型的拟合实验结果，可以合理预测当截面污染物浓度分布状态过度复杂时，三阶二维高斯分布模型拟合准确性会随之降低，此时需增加模型阶数，同时也必要增加监测光路的数目，如果OP-FTIR监测设备和反光镜数量足够，可尝试采用交叉光路的布局方式。

c) 经核算，储罐A的VOCs年排放量为26.1 t，结果处于合理区间。