基于有限元和三维激光扫描技术的储罐变形检测与评估

石 磊，奚 旺，赵亚通，单 克

(1.中国石化大连石油化工研究院，辽宁大连 116045 2. 深圳市燃气集团股份有限公司，广东深圳 518049)

储罐系统负责油品的接收、存储、装车或装船，以及油罐之间倒罐。随着石化行业的发展，储罐向着大型化，集群化迅猛发展。与战略石油储备油罐相比，炼厂、中转油库的油罐输转作业频繁，其安全运行直接关系到燃料的稳定供应[1]。一旦发生泄漏、沉盘、破裂等事故，将可能造成巨大的人身伤亡和环境破坏[2]。由于寒冷气候、油污、杂质和积灰堆积等原因，储罐呼吸阀在长期使用中难免会出现卡死、堵塞、通气量不足等故障，导致罐内气压的变化。石油储罐设计压力较低、稳定性较差，罐壁、罐顶、罐底均较薄，在使用过程中在初始缺陷与罐内负压多因素作用下，会发生抽瘪变形[3-4]。

储罐变形原因分析和修复方式大多依靠经验进行，很少进行科学系统的变形过程模拟[5，6]。现有的储罐变形检测主要针对外观质量检测，对其完整的变形情况往往无法准确、高效地获取。常用的罐壁变形测量方法包括围尺法、光学参比线法和内光电测距法，这些传统测量方法中操作者的劳动强度大、操作危险、测量效率低、误差较大[7-10]。针对某储罐的显著变形问题，采用有限元分析方法进行工况模拟，分析储罐凹瘪变形原因及应力水平，为罐体变形的修复提供技术支撑，采用基于三维激光扫描技术对油罐进行检测及变形评估，为储罐的安全平稳运行提供参考。

1 储罐概况

某油库在例行倒油作业时，由于当地恶劣天气原因致使油罐罐顶呼吸阀结冰堵塞，使得油罐内部形成负压，造成油罐外壁大面积凹陷变形。油罐根据GB50341-2014《立式圆筒形钢制焊接油罐设计规范》进行设计，结构为球形固定弱顶立式油罐，内径11.99 m，高度8.75 m，底板厚度8 mm，球顶板厚度5 mm。罐壁由6层壁板焊接而成，在每层壁板选取6个测点进行超声测厚，测试数据见表1。

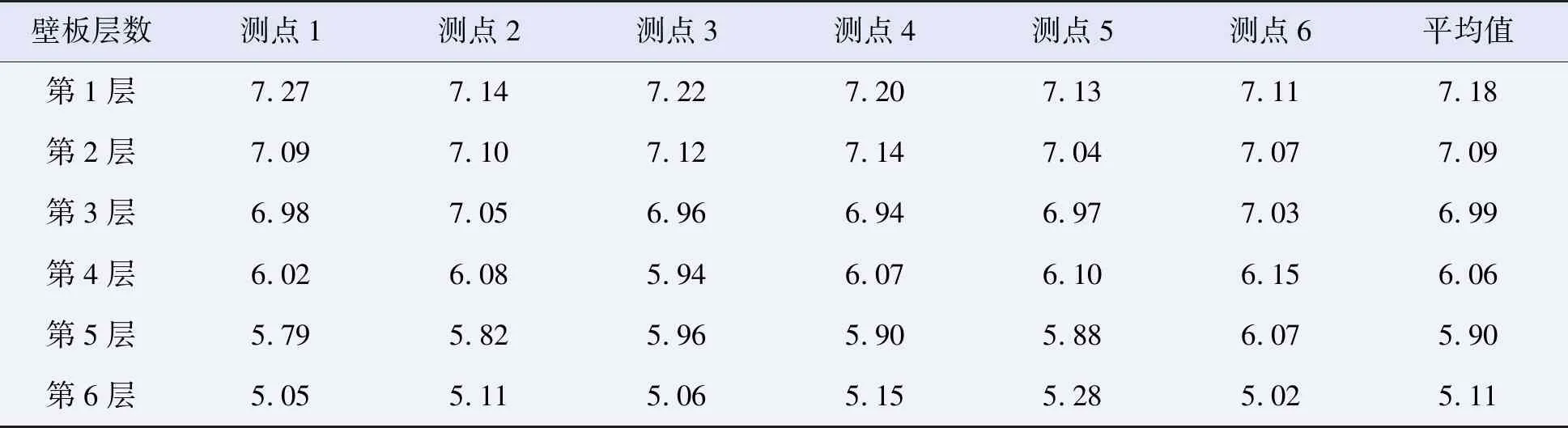
表1 壁板厚度(自下而上)测量结果 mm

罐体变形沿储罐环向分为5个区域，变形中心的高度基本都在距底板高5.2 m处，储罐高度方向的变形大于储罐圆周方向的变形，局部变形深度35～45 cm，如图1所示。

图1 罐壁变形示意

2 变形储罐的有限元评价

采用ANSYS软件建立储罐三维有限元全模型，壁板、底板采用4节点壳单元。罐壁底端全约束，顶端约束径向、切向位移，以及沿切向转角。运行载荷包括罐体及罐顶自重，根据图1储罐因内部形成负压的变形情况，假设罐内为真空的最不利条件，在罐外施加1标准大气压的外压。罐体材料为普通碳钢Q215A，经测试，屈服强度220 MPa，抗拉强度400 MPa，钢材弹性模量E=2.06×105MPa，泊松比0.3，钢材密度7 850 kg/m3。

应力及变形计算结果如图2所示，最大等效应力116 MPa，径向最大变形3.5 mm，发生在罐顶或罐底。可见，理想情况下，内部真空储罐的应力远小于材料屈服强度220 MPa。因此，从强度而言，单一真空条件无法使储罐发生凹瘪变形，储罐变形应属于稳定性问题。

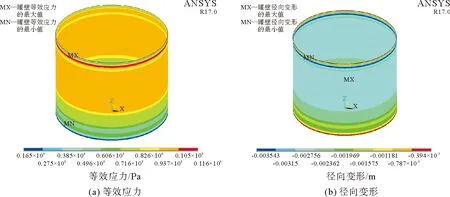
图2 储罐强度计算结果

屈曲分析主要用于研究结构在特定载荷下的稳定性以及确定结构失稳的临界载荷，屈曲分析包括线性屈曲和非线性屈曲分析。线性屈曲分析又称特征值屈曲分析，非线性屈曲分析包括几何非线性失稳分析、弹塑性失稳分析、非线性后屈曲分析。对储罐进行特征值屈曲分析，可获得储罐理想屈曲强度及屈曲模态，结果见图3，屈曲模式为菱形屈曲，与储罐的实际变形模态相吻合，临界屈曲载荷为0.004 MPa。

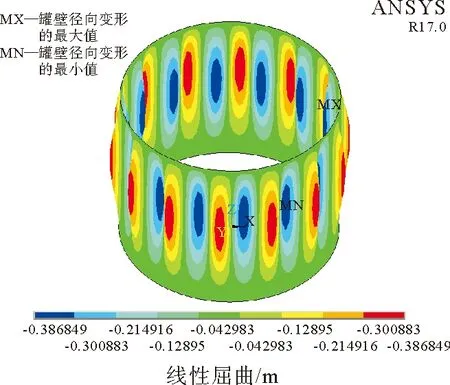
图3 线性屈曲

特征值屈曲分析适用于对一个理想弹性结构的理想屈曲强度(歧点)进行预测，但是无法获得后屈曲模态[11,12]。为获得屈曲后储罐的应力及变形，需采用非线性屈曲分析法进行计算，屈曲模式为菱形屈曲，如图4所示，临界屈曲载荷为0.004 MPa，与特征值屈曲计算结果吻合，证明了储罐在真空状态下的凹瘪变形并非强度问题，而属于结构失稳。临界屈曲状态下，储罐应力最大为9.5 MPa，最大变形为2 mm。结构一旦失稳后，屈曲模态如图5所示，储罐最大应力60 MPa，最大变形为20 mm。由此可判定，储罐凹瘪变形为弹性屈曲。现场采用对变形储罐进行注水的方法进行修复，注水后，变形回弹，几乎恢复原状，证实了有限元分析中储罐变形为弹性屈曲的准确性。

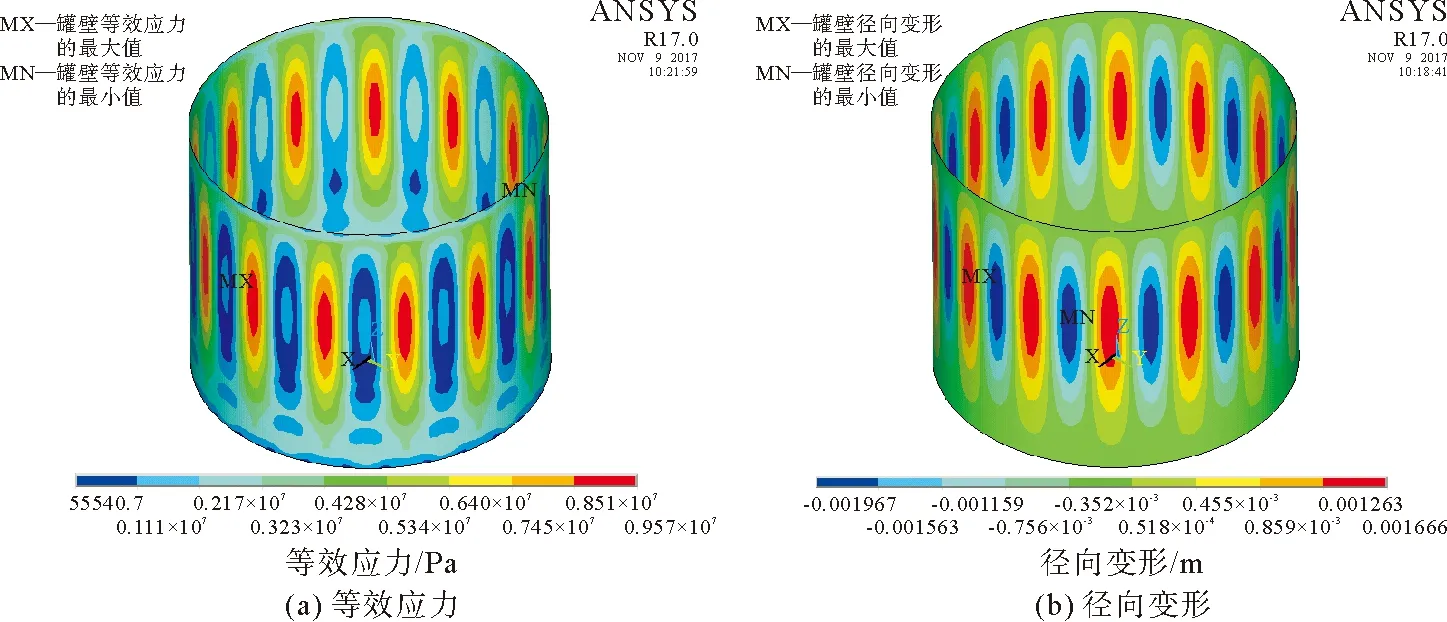
图4 非线性屈曲-临界状态

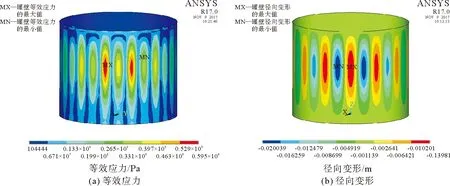
图5 非线性屈曲-后屈曲状态

按照储罐设计的最高液位(8 m)，对变形修复后的储罐进行安全评定。液体静压力从液面到罐底成三角形线性分布[13]，从上到下逐渐增大，以均布载荷的方式加到罐壁板和底板，其表达式如下：

p=rg(H-z)

(1)

式中:p——静水压力，Pa；

r——储液密度，kg/m3；

g——重力加速度，N/kg；

H——储罐内液体的高度，m；

z——距离罐底板的轴向距离，m。

有限元计算结果如图6所示，等效应力最大值为50 MPa，远小于材料屈服强度220 MPa，因此，从强度而言，储罐在8 m液位下属于安全运行。

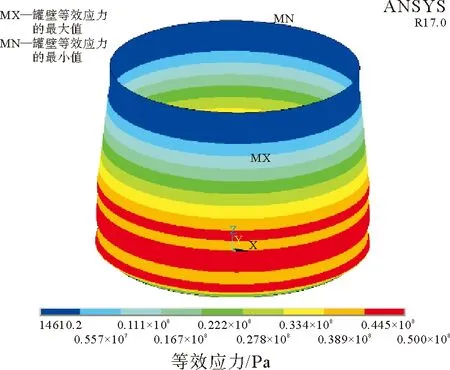
图6 满液位下储罐等效应力

3 基于三维激光扫描的罐体变形检测及评估

三维激光扫描能获取地表实物表面的三维坐标，通过数据经过计算处理和加工实现曲面和模型重建[14-16]。对变形储罐进行注水修复后，采用Trimble TX8三维激光扫描仪进行储罐变形外检测，获得图7所示的罐体三维特征。

图7 变形修复后的油罐

将进油口中心位置指定为0度，逆时针等间隔设置48个点，对每个位置的监测点进行拟合，并计算出相应的偏差，如表2和表3所示。计算不同高度的水平截面圆柱度时，取半径偏差最大值作为目标截面的圆柱度。

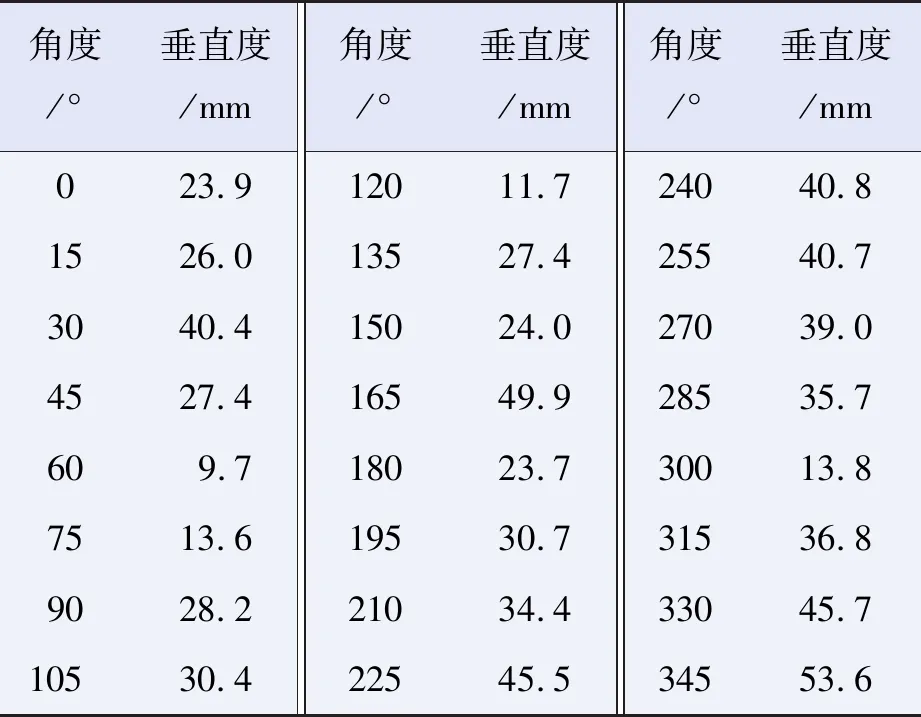
表2 罐体垂直度

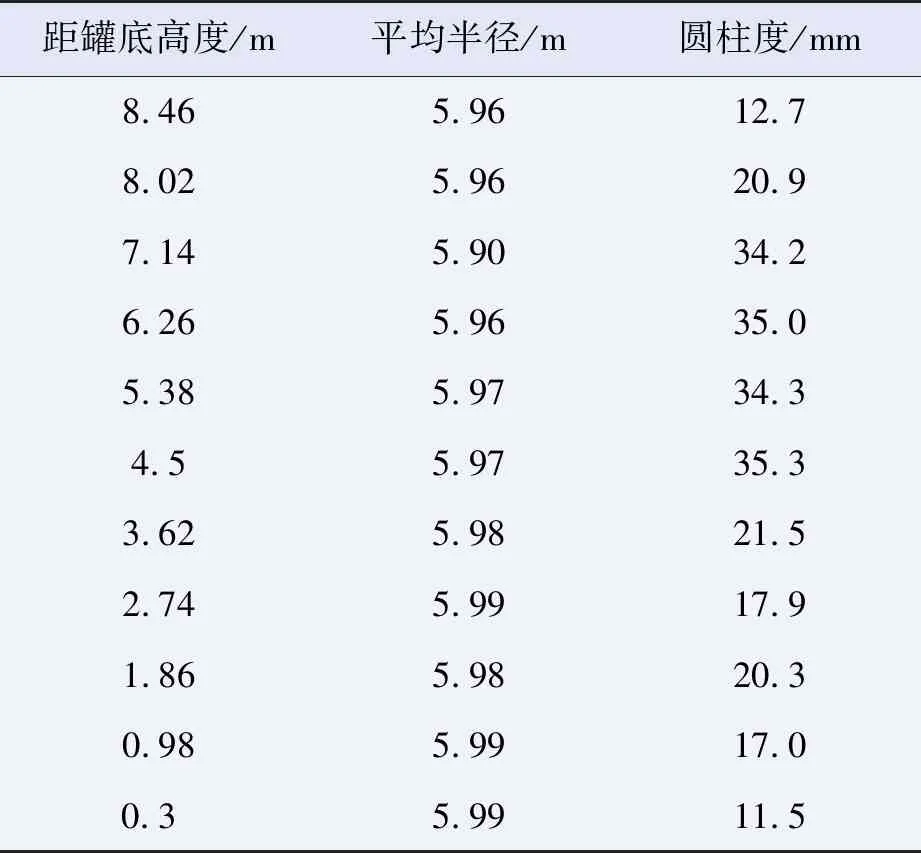
表3 罐体圆柱度

根据API 653，罐壁垂直度的允许偏差，不宜大于罐壁高度的1%，且不大于127 mm，评估储罐的最大垂直度为49.9 mm，未超标。在底圈罐壁0.3 m高度处，内表面任意点测得的半径偏差不超过19 mm，在底圈0.3 m高度处以上测得的半径偏差不超过57 mm，评估储罐的最大椭圆度为35.3 mm，未超标。

4 结论与建议

储油罐作为石化行业重要的存储设备，其安全问题不容忽视。采用有限元及三维激光扫描技术对某凹瘪变形储罐进行评估，结论如下：

a) 采用有限元分析对储罐的变形进行了数值模拟，从强度而言，单一真空条件无法使储罐发生凹瘪变形，储罐变形应属于稳定性问题。特征值屈曲分析表明，储罐屈曲模式为菱形屈曲，临界屈曲载荷为0.004 MPa；非线性屈曲分析表明，临界屈曲状态下储罐等效应力最大为9.5 MPa，后屈曲中储罐最大等效应力为60 MPa，由此可判定，储罐凹瘪变形为弹性屈曲。数值模拟中储罐的屈曲模态与实际变形相吻合。

b) 现场采用对变形储罐进行注水的方法进行修复，注水后，变形回弹，几乎恢复原状，证实了有限元分析中储罐变形为弹性屈曲的准确性。

c) 对变形储罐进行修复后，采用三维激光扫描技术实施罐体变形检测及评估，采用有限元分析方法评估储罐的安全运行液位，结果表明，储罐的垂直度和圆柱度均满足标准要求，在最高设计液位下储罐的强度远小于材料屈服强度，可安全运行。