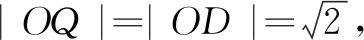高观点视角下的极点极线问题——从2020年两道高考题谈起

敖德兵

(北京师范大学成都实验中学，610017)

一、试题呈现

高观点指导一直是高考命题的热点,在中学数学中若隐若现. 下述试题1(2020年全国I卷理科第20题)、试题2(2020年北京卷理科第20题) 就是以高等几何中的极点与极线知识为背景的试题,若我们站在制高点看问题,其本质可谓一览无余.

(1)求E的方程；

(2)证明：直线CD过定点.

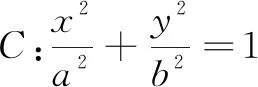
(1)求椭圆C的方程；

二、背景分析

1.极点与极线的几何定义与性质

由高等几何教材[1]可知,过不在圆锥曲线C上的点P引两条割线依次交曲线C于四点E,F,G,H,连EH,FG交于点N,连EG,FH交于点M,则称MN为点P对应的极线,点P为MN对应的极点;同理,PM和点N为一对极线与极点,PN和点M为一对极线与极点.特别地,点P在圆锥曲线C上时,点P的极线是曲线C在点P处的切线.

由性质1,可以证明：

推论2设PQ过有心圆锥曲线C的中心O,则点P,Q关于曲线C调和共轭,当且仅当OR2=OP·OQ,其中R为PQ曲线C的交点.

性质2(等角定理)设A,B为圆锥曲线C的一条对称轴l上的两点(A,B不在C上),若A,B关于C调和共轭,过B任作C的一条割线交C于P,Q两点,则∠PAB=∠QAB.

2.极点与极线的代数表示

已知圆锥曲线C:Ax2+Cy2+2Dx+2Ey+F=0(A2+C2≠0),则称点P(x0,y0)和直线l:Ax0x+Cy0y+D(x+x0)+E(y+y0)+F=0是圆锥曲线C的一对极点与极线.

需要注意的是,对于椭圆,P(x0,y0)不在中心O;对于双曲线,P(x0,y0)不在渐近线上(包括中心O).

3.高观点解答两道高考题

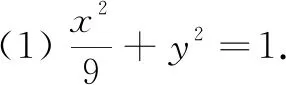
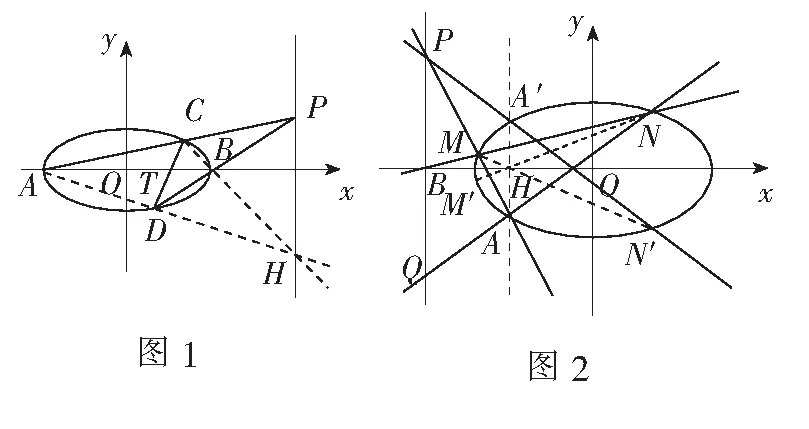
(2)如图1,设CD交x轴于点T,CB,AD相交于点H,由极点与极线的几何定义知TH为点P的极线.

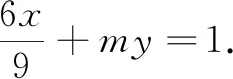
(2)同试题1解答,可知直线x=-4关于椭圆的极点为H(-2,0).

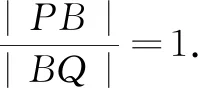
三、考你千遍不厌倦

分析近年的高考解析几何题,不难发现,虽然在试题的呈现手段、材料组织、设问方式等方面不断变化创新,但以极点极线作为背景命制的试题屡见不鲜,真是“考你千遍不厌倦”.以下列举几例,并揭示其极点极线背景.

1.定点定值问题

(1)求点P的轨迹方程;

解(1)x2+y2=1.(过程略)

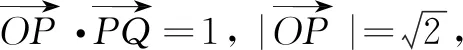
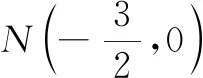
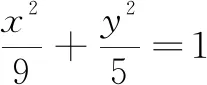
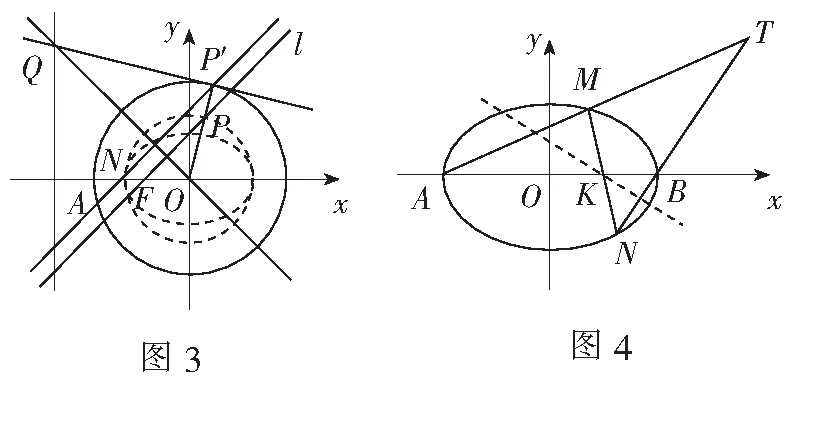
解连MN，交直线AB于点K,则点T对应的极线经过点K.

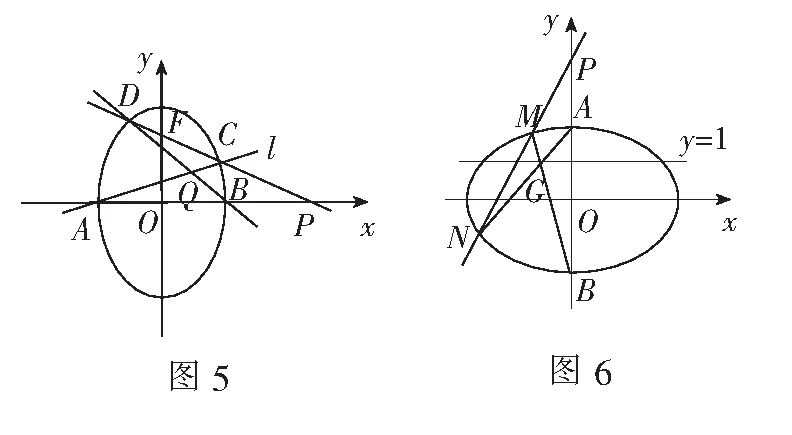
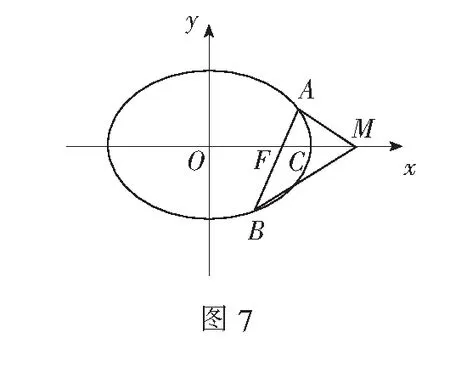
例4(2011年四川高考题)如图5,椭圆有两顶点A(-1,0),B(1,0),过其焦点F(0,1)的直线l与椭圆交于C，D两点,并与x轴交于点P,直线AC与直线BD交于点Q.

(1)求椭圆的方程;

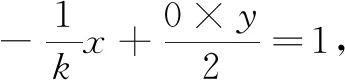
2.三点共线问题

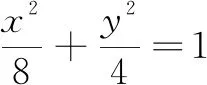
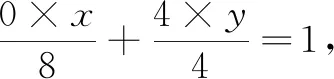
3.等角问题

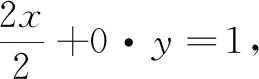
变式(2018年全国高考题)设抛物线C:y2=2x,点A(2,0),B(-2,0),过点A的直线l与C交于M,N两点,求证:∠ABM=∠ABN.

提示计算知点A,B关于抛物线C:y2=2x调和共轭,由等角定理可得证.

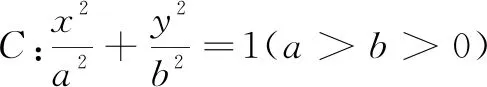
(1)求椭圆C的方程,并求点M的坐标(用m,n表示);

(2)设O为原点,点B与点A关于x轴对称,直线PB交x轴于点N.试问:y轴上是否存在点Q,使得∠OQM=∠ONQ?若存在,求点Q的坐标;若不存在,说明理由.

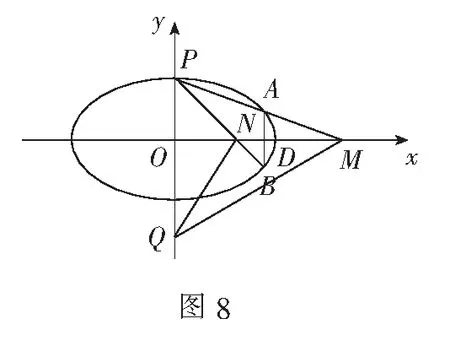
(2)设y轴上存在点Q,使∠OQM=∠ONQ(如图8),则由∠QOM=∠NOQ,得∆OQM∽∆ONQ,故|OQ|2=|ON||OM|.

设点P关于x轴的对称点为P′,则P′A交x轴于点N,P′B交x轴于点M,于是点N在点M的极线上,点M,N关于椭圆调和共轭.设椭圆的右顶点为D,由椭圆中心O在直线MN上,结合推论2,得|OD|2=|ON||OM|.