数学建模的实践与探究
——从一节相关疫情的概率分布应用课谈起
姚 杰 戴静君
(江苏省锡山高级中学,214174)
新一轮的课程改革进一步拓展了概率与统计这块内容.本文以概率分布的应用为例.探索如何用数学建模解决实际问题的能力,培养学生的数学核心素养.
一、基本情况
本节课是概率分布的一节应用课,重在培养学生从实际问题概括出数学模型和解决数学模型的能力.主要内容是引导学生通过建立模型,利用随机变量的数字特征来预测口罩的检验情况,并对疫苗检测给出的几种方案,计算数学期望,给予评价.重点是会用排列组合,二项分布,随机变量数学期望解决实际问题,难点为对实际问题进行数学抽象,利用导数研究函数的最值.
二、教学过程
师:2020年,注定是不平凡的一年,目前全球范围内疫情还没有完全控制.但是,中国作为一个有担当、有责任感的大国,不仅仅在国内有效控制住了传染源,确诊病例在急剧减少,还力所能及地给其他国家伸出援手,提供了抗疫所需的医疗物资,比如口罩、试剂检验盒、防护服等.同学们,今天我们也来出点力,用所学的知识,去帮企业检测口罩的合格情况,去帮医务人员算算样本怎么检验才能更加高效.
例1某工厂生产N95型口罩成箱包装,每箱200件,出厂前要对产品进行检验,如果检验出不合格品,则更换为合格品.检验时,先从这箱产品中任取20件检验,再根据检验结果决定是否对余下的产品做检验.设每件产品为不合格品的概率为p(0 问题1记20件产品中恰有两件不合格品的概率为f(p),求f(p)的最大值点p0; 师:具体说说你这个函数怎么来的? 师:函数表示出来后,怎么去求它的最大值点呢? 师:大家觉得可以吗? 生2:不可以!因为上面的做法中r是整数,这里的p是(0,1)内的任意实数. 师:非常好. 设计意图让学生会用二项分布解决相关概率问题,并用导数研究函数的最值. 问题2以上述确定的p0作为p的值.已知每件产品的检验费用为2元,若有不合格品进入用户手中,则工厂要对每件不合格品支付25元的赔偿费用.若不对该箱余下的口罩做检验,这一箱口罩的检验费用和赔偿费用的和记为X,求E(X). 生4:随机变量X表示的是检验费用和赔偿费用的和,第一部分检验费用是相对固定的20×2=40元,第二部分赔偿的费用需要根据剩下的180件口罩的合格情况,而每一个口罩是否合格仍然是相互独立的,可以记Y表示180只口罩中不合格的数量,则Y也服从二项分布,所以X=40+25Y,先求出Y的数学期望为180×0.1=18元,所以X的数学期望为490元. 师:这位同学引入了一个变量Y过渡,从而求出了结果. 设计意图学会建立随机变量之间的关系,服从二项分布的随机变量会求其数学期望. 问题3以检验和赔偿总费用的期望值为依据,是否应该对该箱余下的口罩做检验? 生5:需要比较两种情况费用的数学期望. 师:说说你的结果. 生5:由问题2余下口罩不检验费用的数学期望为490元.如果对余下的口罩也进行检验,那么共需要200×2=400元,所以应对余下的口罩进行检验. 师:检测口罩为了让我们有效地预防疫情,而疫苗的研发更是迫在眉睫. 例2冠状病毒的疫苗研发是一个复杂的过程,包括锁定疫苗、疫苗初制备、动物实验、临床试验.在动物实验环节,需要对动物的血液进行检测. 问题1假设有5份血液样本,其中只有2份样本为阳性,求恰好经过4次检验就能把阳性样本检验出来的概率. 师:对吗? 设计意图会运用排列组合解决古典概型问题. 问题2现有n(n∈N*)份血液样本,有以下两种检验方式: 方式1逐份检验,需要检验n次; 方式2混合检验,将其中k(k∈N*且k≥2)份血液样本取样混合在一起检验.若结果为阴性,这k份血液全为阴性,因而检验一次就够了.如果结果为阳性,为了明确这k份血液究竟哪些为阳性,就要对这k份再逐份检验,此时检验总次数为k+1次.假设每份样本的检验结果都是独立的,且每份样本是阳性结果的概率为p(0 师:很好. 设计意图会列出随机变量的概率分布,并求数学期望. 问题3假设该疫苗的治愈率为90%,现对10 000只被感染的动物注射疫苗后进行抽血化验,有三种方案:① 逐一化验;② 按4个动物一组分组,混合检验;③ 按4个动物一组分组,混合检验.问哪种方案更优?(参考数据:0.94=0.66,0.95=0.59,0.920=0.122) 生9:哪种方案更优,就是比较哪种方案检验次数少,需要求出三种方案次数的数学期望.方案①的期望是10 000,方案②每组40个动物,一共有250组,记X表示每组检验次数,根据问题2,E(X)=(40+1)-40×0.940=40.404 64,所以检验总次数期望为10 101.16.同理,方案③的数学期望是5 939从而判断方案③更优. 师:其实第3问是第2问的应用,我们只要代入数据,就可以得到所需结果. 师:很好!今天我们完成了口罩的检测和疫苗的检验,但是很多问题往往不止一种解决方法,希望课后大家能够消化课堂内容,继续探究,如有新想法,下节课再一起分享. 1. 巧改课后习题 本节课例2来源于书本课后习题,根据当前疫情进行改编和整合,是一个集排列组合、比较随机变量数学期望和导数为一体的综合问题,有一定难度. 2. 体验数学建模 数学建模是对现实问题进行数学抽象,用数学语言表达问题,用数学方法构建模型解决问题.过程主要包括:发现问题、提出问题,分析问题、建立模型,确定参数、计算求解,检验结果、改进模型,最终解决实际问题[1].本节课在课前、课上、课后尽可能让学生体验建模的全过程,使学生学以致用,并且认识到数学建模在医学、工程技术等诸多领域的巨大作用,增强创新意识,提升实践能力. 3. 学生自主探究 本节课主要采用了探究式学习的方式.首先课前向学生介绍课题内容,提供课堂讲义.然后让学生分组讨论,提出问题,尝试寻找解决问题的方案.再通过课堂,对各种具体方案的实施进行分析,接着去处理数据,形成结果,最后对所得结果进行评价.通过这种学习方式,学生会觉得生动有趣,更有学习的信心.与此同时,教师的教学也会更有价值,使教师的教学设计能力、分析和组织教材的能力、开拓创新的能力都有提升. (1)数学建模是进入高校后,学生才会正式学习到的一门课程,但是如果把平时应用题经过整合改编,可以让学生更早接触,提升整体的数学素养.但这只是初步的建模,其一,所学的模型可以完美地契合题干;其二数据相对好算;其三,算出结果后容易下结论.而一般数学建模需要根据现实情况,多角度总结,把结果解释得更加科学.中学阶段的数学建模相比常规课对于教师有着更严格的要求,课堂上学生的各种想法,需要教师能够第一时间分析,除了要对题目本身吃透,还需要有着出色的语言能力,做到用词准确,叙述精炼,具有逻辑性、启发性. (2)江苏在新高考背景下需要抛弃老高考中一些既定的模式,应用题可能不再倾向于三角函数、导数、基本不等式等,统计、概率分布也会越来越多的涉及,所以需要学生思维更广,能力更强,才能从容应对.同时在新高考中会增加阅读量,而数学建模题干较长,信息量大,需要学生仔细阅读寻找条件,正好可以达到锻炼的效果.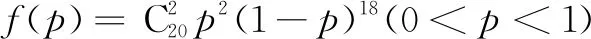




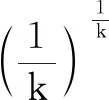

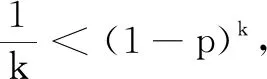
三、教学反思
四、教学启示

