FDM零件表面粗糙度偏最小二乘回归建模研究

黄昕龙，花海燕，陈世辉

(1.福建江夏学院 工程学院，福建 福州 350108；2.福建工程学院 机械与汽车工程学院，福建 福州 350118)

随着FDM工艺日益成熟，其应用也越来越广泛[1]。成型件的表面质量精度低，稳定性差等问题成为了制约该技术发展的主要因素之一。目前，研究阶梯效应的成型机理，分析阶梯效应与打印工艺参数的改善关系成为主流方向[2-3]。国内外许多学者从成型层厚度、成型面角度以及打印材料等角度出发进行了深入研究，取得了显著成果[4-7]。但仍然存在许多不足，如：阶梯效应无法针对水平成型面或垂直成型面的表面粗糙度给出有效的解释；现有很多学者对表面精度提出了一系列的优化策略，主要是基于用户可调整的初始工艺参数，虽然易于调节，但存在工艺参数的组合优化不可控，微小调整量对表面质量的影响波动大等问题。

基于此，本研究在FDM工艺挤出材料截面形状的基础上，深入探讨水平成型面的表面粗糙度形成几何机理，分析设备固有参数对表面质量的影响，为成型设备的优化与开发提供导向。

1 模型构建

1.1 丝材的宽度模型

图1 挤出丝截面模型Fig.1 Cross-section of extruded filament

图2 三次参数曲线Fig.2 Cubic parametric curve

(1)

式中，φ(u)=(1,u,u2,u3)为参数曲线的多项式基；a=(a0,a1,a2,a3)'为系数矢量。通过规定曲线两端点p(0)、p(1)和端点切矢r(0)、r(1)来确定该系数矢量，可得系数矢量的矩阵形式为：

(2)

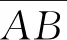
为方便确定三次曲线曲线段的几何特征与形状类型，引入u=0,1两端点切矢的形状仿射不变量λ和μ，二者表示曲线段首尾两端切矢。对于呈现扁平状且无明显凸起的正常成型的丝材沉积截面，满足截面轮廓的三次曲线段内无拐点的几何形状特征，即此时曲线拐点不在0≤u≤1内，其拐点数为1～2个，若为2个拐点则存在单侧与双侧分布的情况。根据分布判别情况可知，三次曲线段的具体形状可用唯一的λ和μ表示[9]。根据仿射不变量λ和μ的定义，可用式(3)表示L：

(3)

整理式(2)和式(3)，可得曲线参数表达式为：

(4)

式中，元素aij，i=2,3,4、j=1,2为形状系数，与端点切矢及仿射不变量有关。在具体成型过程中，由端点切矢及仿射不变量确定的截面线宽曲线，所呈现的形态与打印工艺参数密切相关，因此在不考虑随机因素的情况下，可认为丝材的线宽形态存在确定性，这是由现有FDM成型设备工艺参数的确定性及合理性决定的。

最后，根据垂直截面形状，将曲线进行坐标变换，即逆时针转过γ角，利用坐标转换矩阵R(γ)的关系式可得旋转后的三次参数曲线pt(u)：

(5)

1.2 粗糙度几何机理

在FDM工艺中，相邻扫描线路上的挤出丝通过喷嘴的加热与挤压实现相互黏结，经历接触、扩散与黏结3个阶段。大量研究表明，丝材的挤出温度Tz越高，则ABS等聚合物共混物浸润的有效时间t越长，相邻丝材间的扩散程度与黏结强度也就越高，这在一定程度上对成型平面的微观形状造成影响。考虑到ABS材料熔融状态及高温分解碳化等问题，现有FDM打印设备的丝材挤出温度Tz一般控制在180～280℃。Tz与t关系可用关系式(6)表示：

(6)

式中，Tg为热塑性材料的玻璃化转变温度，对于ABS材料而言，其玻璃化转变温度Tg=94 ℃；Te为打印设备成型室温度；η为热变化系数，与打印材料的热特性及截面形状有关。

根据实际水平成型面的成型情况，以直线往复扫描为例，假设打印平面不存在空间约束的情况，相邻沉积层截面的立面模型如图3所示。图3中描述一种均匀理想模型：Ac(j)为j段扫描路径打的横截面积；Sg为相邻丝材间隙；Sb为相邻丝材在有效扩散时间内的浸润面积。鉴于保持熔融沉积的均匀一致，打印喷头的挤出速度与扫描速度不变情况下，显然有Ac(1)=Ac(2)=…=Ac(j)=…=Ac(k)其中k为扫描路径总数；扫描路径间隔均匀，其扫描间距为b。为保证成型强度和表面质量，相邻沉积层存在一定空间约束，即扫描间距b小于挤出丝最大宽度W，从而使得间隙不会太大，对于商用设备，为保证打印质量稳定，扫描间距b为设计优选后的固定值。此时，类似于机加工中的残留面积，相邻成型面间的间隙作为轮廓谷，从而形成一种理论粗糙度。

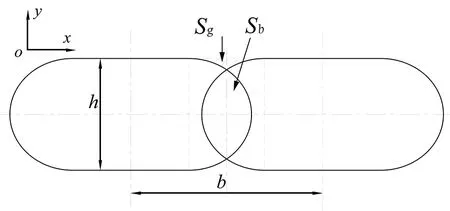
图3 沉积层间隙立面图Fig.3 Elevation of sedimentary interstitial spaces

考虑到理想打印表面的周期性与对称性，采用轮廓算术平均中线作为粗糙度评定基准线，选取评定长度为lr。根据定义，评定基准线将实际轮廓分为上、下部分，满足上部分面积之和FU与下部分面积之和FD相等，即FU=FD。评定参数采用算术平均偏差Ra可表示为：

(7)

在评定长度内，间隙作为轮廓谷所占面积较小，评定基准线接近成型平面，此时Ra可近似表示为：

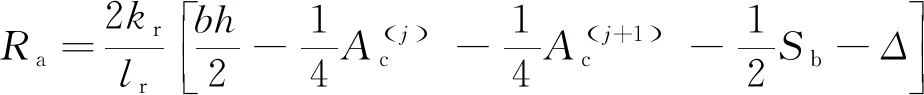
(8)

式中，kr为单位取样长度内Sg个数。

因此，根据理论粗糙度评定机理，可以建立基于工艺参数的粗糙度非线性模型，其具体模型函数可表示为：

(9)

式中，d0为打印喷嘴直径；ve为挤出速度，其取值为打印设备缺省值；vf为打印速度；Ψj=(akp)为三次参数曲线形状系数构成的多项式函数；ϑ为黏结速度相关系数，单位为s-1，考虑到丝材堆积时侧向的挤压力需要由路径规划中的丝材间距给出，当扫描路径间距b一定时，相邻丝材从浸润到粘结的速度保持不变，即在打印条件一定时可认为系数ϑ为常量；δR为误差项。

2 模型参数估计

根据上述对线宽模型及粗糙度机理的分析，可以确认可控变量与因变量粗糙度之间的回归模型。在模型方程中，h、vf和Tz作为非随机自变，Ra作为因变量，分别记为xi和y。考虑在自变量非单一维数且自变量与因变量之间为非线性关系，根据拟线性回归模型的思想，对Ra的模型函数进行转换，即

y=f1(x1)+f2(x2)+f3(x3)+ε

(10)

式中，fi(xi)，i=1,2,3为自变量函数式；ε为误差项，表示除了自变量之外干扰因素对Y的影响以及堆叠层的惯性误差。

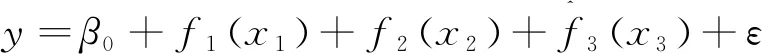
(11)

具体展开，即：

(12)

其中，βj、β3,l为模型的待定参数，并且

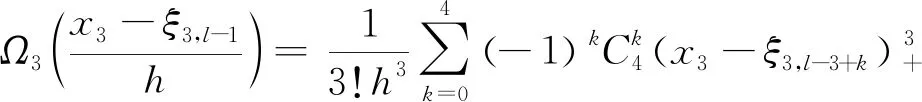
(13)

式中，ξ3,l-1、h、M分别为x3上划分的区间分点、分段长度及分段个数，其中

(14)

根据上述建模思路，通过以下5个步骤即可计算获得模型参数。

(1)对自变量x3进行3次B样条变换。

1)确定分段个数M，求得区间分点ξ3,l-1；

2)对x3做3次B样条变换：

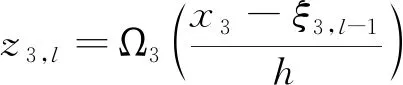
(15)

(2)对所有自变量进行标准化处理，即

(l=0,1,…,M+2;j=1,2;i=1,2,…,n)

(16)

(17)

(3)对式(17)进行偏最小二乘回归(PLS)建模，提出最多的PLS成分数，并求得回归系数α3,l。

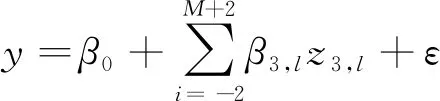
(18)

(5)将回归系数及样条函数变换式(15)代入式(18)，得到y关于X非线性回归模型。

根据上述流程，结合原始数据表(X,y)可建立基于3次B样条变换所构建的局部非线性模型，从而确定工艺参数与粗糙度二者间的函数关系。

3 实验与分析

3.1 实验数据获取

实验采用ABS作为打印材料，使用封闭式的桌面级FDM打印机作为打印设备。如图4所示，设计并打印20 mm(长)×20 mm(宽)×15 mm(高)的立方试件用于表面的粗糙度测量。由于试件底部作为支撑生成面，表面质量无法控制，因此选择试件的顶面，测量仪器选用手持式表面粗糙度测量仪(Mitutoyo SJ-210)，其最小测量精度为0.001 6 μm。

图4 实验立方模型Fig.4 Test specimens

结合所构建的粗糙度模型采用3因素3水平正交试验法进行实验，具体的因素水平见表1。

表1 因素水平表Tab.1 Factor levels

3.2 PLSR模型生成与分析

在多元线性回归中，提高自变量维度可在一定程度上降低标定误差，但是太高的成分数容易造成模型过度拟合，一般可通过不同成分数下的误差标准差Sh或预测误差标准差Rh进行判断

(19)

式中，Sh的大小反映了成分为h时因变量的误差标准差。一般而言，随着h的增大，Sh会逐渐减小，若Sh不减小反而增加时，表明成分个数太大已造成过度拟合；Rh则反映了成分数为h时，在交叉舍一方法下计算的预测误差标准差，与Sh同理，若其减小不明显或者增加时，成分数的增加将造成过度拟合。

图5是h为1～6时，Sh与Rh的变化情况。从图5可看出，由于样本数据较少，在实际数据处理中无法通过Rh获取成分数的最优点，因此本文直接采用回归数据下的误差标准差进行最优判断，即选取成分数h=4。根据实验数据，以h、vf、Tz作为自变量，并进行样条变换，同时以平面粗糙度Ra作为因变量，最后通过软件编写程序进行PLSR迭代计算，求得标准化回归方程

图5 误差标准差Sh和预测误差标准差RhFig.5 Standard deviationSh of error and standard deviation Rhof prediction error

(20)

y=4.874 0+0.060 3x1+39.942 9x2-

0.904 1z3,0-0.226 0z3,1+2.657 5z3,2+

0.890 4z3,3+0.904 1z3,4-0.664 4z3,5-

2.657 5z3,6

(21)

最后将样条函数变换式(21)带入转化为实际参数，即求出Ra。从回归方程可以看出，水平打印表面的粗糙度主要受打印速度与丝材挤出温度的影响，而打印分层高度对其影响有限。图6是在打印分层高度h=0.06 mm时，根据回归方程模拟的水平面粗糙度，从图中可看出，随着打印速度增大，水平面粗糙度呈现整体增大的趋势；对于丝材挤出温度，则是在可调区间内存在最适温度，这与实验表现出来的结果基本相符。

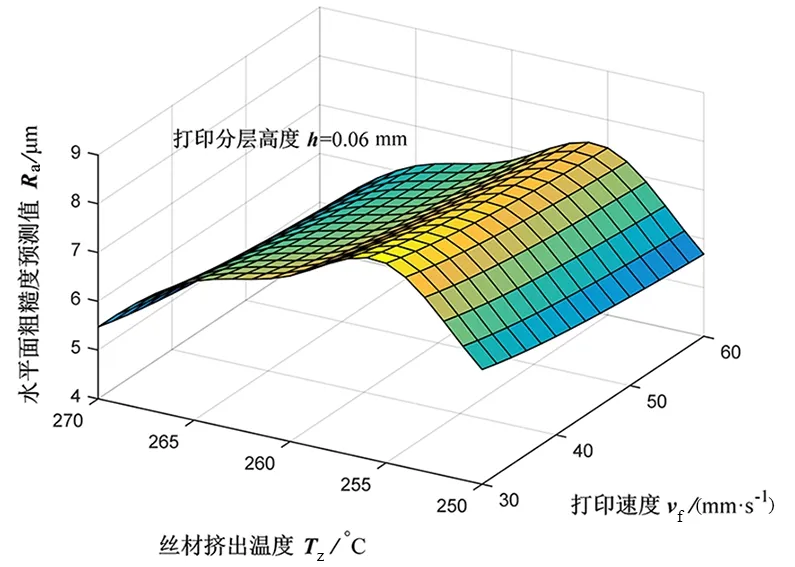
图6 不同丝材挤出温度及打印速度下的水平面粗糙度变化曲面Fig.6 Surface of horizontal roughness variation under different extrusion temperature and printing speed

3.3 数据校验

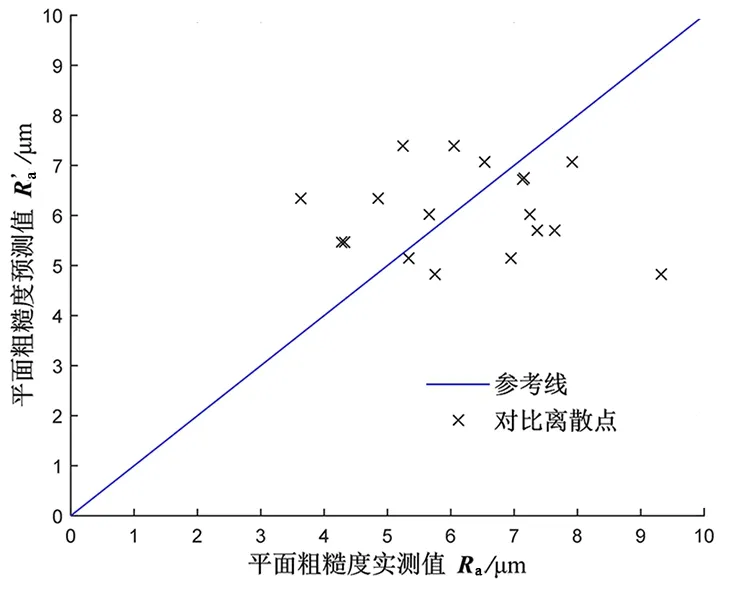
图7 PLSR模型预测值与实测值的对比结果Fig.7 Comparison results of predicted values and measured values with the PLSR model

4 结语

通过提出一种基于参数三次曲线与多段直线拟合的丝宽模型，结合粗糙度的几何机理，对FDM打印件的水平表面粗糙度进行建模，得到了水平表面粗糙度的一般理论模型，并在此分析上，从多个加工参数中选择3个主要参数作为控制变量，并通过基于样条变换的非线性偏最小二乘回归(PLSR)，实现了粗糙度参数预测模型的建立。PLSR模型较为直观明了地解释了主要参数对水平面粗糙度的影响程度与方向。最后通过不同的实验样本数据对回归预测模型完成了校验，获得了较好的预测精度。该分析方法从FDM成型件的水平表面粗糙度出发，为FDM打印设备的设计与调试提供理论依据与重要参考，提高了打印质量预测的效率。