梅花形阵列粗糙床面明渠紊流特性
钟 亮 ,葛晨曦,孙建云
(1. 重庆交通大学 国家内河航道整治工程技术研究中心,重庆 400074;2. 重庆交通大学 水利水运工程教育部重点实验室,重庆 400074)
梅花形阵列粗糙是指床面粗糙单元彼此相隔一定距离且呈梅花形排列的粗糙形态,在天然河流中普遍存在,在河工模型床面加糙中也广泛应用[1]。受床面颗粒绕流作用的相互影响,梅花形阵列粗糙床面明渠水流紊动特性复杂,并受到了国内外学者的较多关注。紊动强度方面,Baki等[2]研究了卵石阵列粗糙床面明渠紊流,提出了紊动强度的计算公式;Papanicolaou等[3]分析了阵列卵石周围水流的紊动强度,探讨了床面小尺度粗糙对水流的干扰作用;Lawless等[4]研究了梅花形阵列粗糙卵石簇对紊动强度的影响。雷诺应力方面,Balachandar等[5]对阵列粗糙床面明渠紊流参数进行了象限分析,得出平均雷诺应力与喷射和清扫事件正相关,与向外和向内事件负相关;Lawless等[6]讨论了非均匀粗糙卵石簇周围水流横向流动对雷诺应力的影响;Robert等[7]分析了雷诺应力空间分布与砾石间距及粗糙度的关系。紊动能方面,Sarkar等[8]研究了粗糙床面大型砾石阵列紊动能的变化特点,发现在床面附近清扫事件起控制作用,随着垂向距离的增加,喷射事件占主导地位;Baki等[9]基于典型鱼道中的梅花形阵列粗糙床面明渠紊流试验,探讨了紊动强度和紊动能的函数关系。梅花形阵列粗糙颗粒间的区域往往是鱼类洄游和船舶航行通道所在,然而,现有研究主要针对颗粒周围某个特定位置或颗粒所在纵剖面,水流紊动特性参数在颗粒间的沿程变化特征、不同象限紊动参数分布差异等方面的研究仍较薄弱,相关问题研究还有待开展。
本文以不同颗粒大小和排列间距形成的多种梅花形阵列粗糙床面为例,选择位于两排颗粒中间的水槽纵向中轴剖面进行分析,基于PIV水槽明渠紊流试验资料,研究紊动特性参数(紊动强度、雷诺应力、紊动能)的垂线分布规律和沿程变化特征。
1 资料与方法
1.1 水槽试验
试验在高精度整体变坡PIV水槽中进行,水槽长12 m、宽0.25 m、高0.25 m,入口放置整流格栅,出口设置合页式尾门。试验采用了3种梅花形阵列粗糙床面(床面B1、B2、B3),床面颗粒均为圆形玻璃珠,颗粒大小和间距参考了河工模型试验实际情况,颗粒直径分别为6、6和9 mm,纵向(水流方向)间距Lx分别为24、48和48 mm,横向(与水流正交方向)间距Ly均为24 mm,颗粒阵列形态及水槽试验见图1。根据试验布置,水槽上段2.4 m为光滑段,中段8.6 m为粗糙段,下段1.0 m为尾门段;试验段流场采集窗口中部距水槽进口8 m,距水槽出口4 m,进、出口长度满足紊流充分发展和消除水流扰动的要求[10]。试验流量采用电磁流量计测量,底坡采用水槽进、出口断面的调坡测针控制,水深通过调节尾门开度调整,并保持水面比降与底坡一致,试验水流为均匀流,流场应用二维高频PIV系统沿位于两排颗粒中间的水槽纵向中轴面采集。PIV系统组成、试验参数控制、流场样本容量等详见文献[11]。

图1 颗粒阵列形态及水槽试验Fig. 1 Particle array morphology and flume test
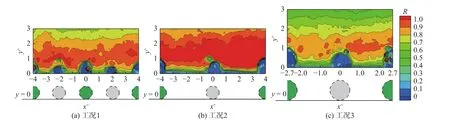
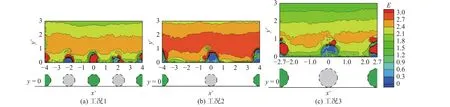
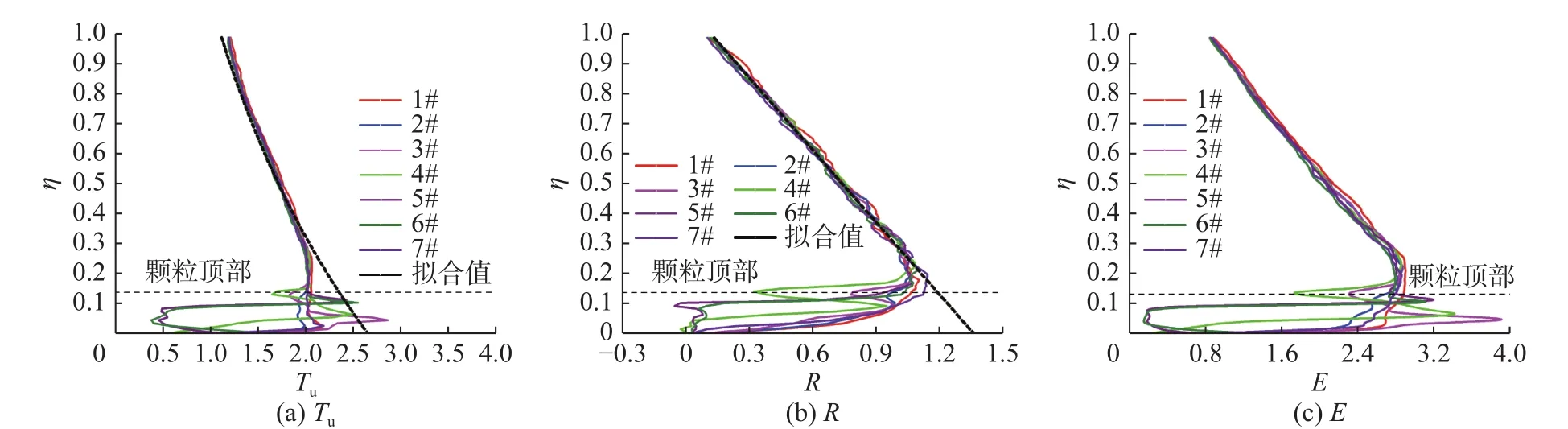
选用表1所示3种工况的试验数据进行研究,粗糙雷诺数Re*大于70,属水力粗糙床面。宽深比B/h=5.57~5.72 > 5,水槽中心区域水流满足二维流动条件[12-13]。相对水深h/d= 4.98~7.49,床面属Bray等[14]定义的中尺度粗糙(3 表1 试验工况参数Tab. 1 Summary data of experimental run 无量纲化后的纵向紊动强度Tu、雷诺应力R和紊动能E的计算公式分别为: 式中:u、v分别为纵向脉动流速和垂向脉动流速;n为样本容量;为沿程各垂线的摩阻流速。对于由u、v组成的脉动流场(u, v),按其数值大小可分为4个象限(见图2),每个象限均代表了1类紊流事件:Q1向外事件代表高速流体的向外运动,Q2喷射事件代表床面附近低速流体向上扬起,Q3向内事件代表低速流体的向内运动,Q4清扫事件代表上部高速流体向床面冲击,其中Q2、Q4事件是紊流产生和维持的关键过程。为探讨不同象限紊动特性参数的变化特征,研究中还计算了各象限雷诺应力Rj和紊动能Ej(j为象限编号,j=1~4),此时ui、vi为该象限的脉动流速,n为该象限的样本容量。需要指出,因计算象限紊动参数和总紊动参数时采用了各自的样本容量,总紊动参数在数值上并非为象限紊动参数简单求和的结果。 图2 象限分析方法示意Fig. 2 Sketch of quadrant analysis method 定义沿程位置参数x+= x/d,x为从流场采集窗口中部颗粒起算的沿程距离,x+= 0表示该颗粒中心,x+<0表示该颗粒中心上游,x+> 0表示该颗粒中心下游。定义垂向位置参数y+= y/d,y为从颗粒底部平面起算的距床面距离,y+= 0表示颗粒底部平面,y+= 1表示颗粒顶部平面。定义沿纵向的颗粒粒径范围为颗粒区(比如,−0.5 ≤ x+≤ 0.5),颗粒区以外的区域为粒间区。图3~5分别给出了距床面3d范围内的无量纲纵向紊动强度Tu、雷诺应力R和紊动能E分布云图,结果显示: (1)在颗粒顶部以上区域(y+> 1),Tu、R、E沿程基本呈条带状变化,受颗粒影响较小,而在颗粒顶部以下区域(y+≤ 1),Tu、R、E受颗粒影响明显,沿程变化相对复杂,表现出一定的周期性和分区性,并可分为颗粒区和粒间区,各区紊流特性参数差异明显。 图3 纵向紊动强度的分布云图Fig. 3 Distribution cloud map of longitudinal turbulence intensity 图4 雷诺应力的分布云图Fig. 4 Distribution cloud map of Reynolds stress 图5 紊动能的分布云图Fig. 5 Distribution cloud map of turbulent kinetic energy (2)纵向紊动强度Tu在颗粒顶部以上区域基本呈条带状分布,颗粒顶部及其以下区域Tu分布较为复杂,该区域颗粒区Tu分布形态接近圆形,而粒间区Tu分布与颗粒直径d、纵向间距Lx有关,d越大,Lx越小,Tu分布形态越复杂。 (3)雷诺应力R在垂线高度(0.5~2.0)d范围内的变化较为复杂,该范围之外的R分布基本呈条带状;在(0.5~2.0)d高度范围内,颗粒区的R总体小于粒间区;颗粒顶部以下区域粒间区R的分布形态与颗粒形状较为相似,接近圆形。总体而言,d越小,Lx越大,R数值越大。 (4)紊动能E的分布形态与纵向紊动强度Tu具有相似性,颗粒顶部以上区域的E条带分布明显,颗粒顶部以下区域E分布相对复杂,特别在颗粒区,该区域E分布形态接近圆形,粒间区的E也受颗粒直径d和纵向间距Lx等因素的影响。 由于颗粒排列和参数变化具有周期性,考虑到异排颗粒影响,各试验工况的排列周期Px= 0.5Lx=(2.0~4.0)d。以工况2为例,在流场采集窗口中部颗粒中心的上、下游0.5Px范围内选择7条垂线(1#~7#),各垂线的沿程位置参数x+= −2.0、−1.0、−0.5、0、0.5、1.0、2.0。图 6给出了参数Tu、R和E的垂线分布,分析可见: (1)颗粒顶部以上区域不同垂线的Tu沿水深变化基本一致,数值上也较为接近。颗粒对Tu的影响主要集中在颗粒顶部以下区域,垂线距颗粒越近,影响越显著;粒间区Tu沿垂线变化较为平缓,而颗粒区及其略下游(3#~6#垂线)的Tu波动剧烈,分布曲线呈“S”状和倒“L”状,数值上较粒间区的Tu明显减小。对Tu垂线分布的拟合表明,Tu在垂线上服从指数分布Tu=2.66exp(−0.88η),这与Nezu等[15]针对密排粗糙床面的相关研究结果较为吻合,但拟合系数由2.26增大至2.66,说明梅花形阵列粗糙床面的Tu在数值上较密排粗糙时更大些。 图6 紊动参数的垂线分布Fig. 6 Vertical distribution of turbulence parameters (2)颗粒顶部以上各垂线的R相互交织,差异总体不大。颗粒对R垂线分布的影响也主要体现在颗粒顶部以下区域,该水深范围粒间区的R随水深比η的减小而急剧减小,颗粒区及其略下游(3# ~ 6#垂线)则表现出一定的波动性,尤其在颗粒中心所在的4#垂线,R分布曲线呈“S”状,其下游垂线的R分布曲线则呈倒“L”状,在颗粒顶部以下极小范围内骤减。拟合显示,R在垂线上服从线性分布 R =1.25(1−η)+0.114,与光滑床面的传统分布方程 R =1−η存在一定差异。 (3)颗粒顶部以上区域各垂线的E分布与Tu、R分布较为类似,相互差异不大。而颗粒顶部以下区域,沿程距 x+= −0.5 ~ 1.0 范围内各垂线(3# ~ 6#垂线)的 E 波动明显,3#、4#垂线的 E 分布曲线呈“S”状,5#、6#垂线的E分布曲线呈倒“L”状。颗粒顶部以下区域的紊动特性参数Tu、R和E变化剧烈主要与颗粒阻水绕流、水流动量和能量在较小范围内重新调整分配有关。 2.3.1 象限紊动参数 从前文分析可知,沿程各垂线Tu、R和E的差异主要体现在颗粒顶部以下区域。为探讨不同象限紊动参数的沿程变化特征,采用1.2节所述方法计算了颗粒顶部以下区域的象限紊动参数。由于纵向紊动强度Tu仅与纵向脉动流速u有关,因此这里仅分析雷诺应力R和紊动能E。以窗口中部颗粒上、下游的1个排列周期范围为例,图7给出了各象限雷诺应力垂线平均值的沿程变化。 图7 各象限雷诺应力垂线平均值的沿程变化Fig. 7 Longitudinal variation of vertical average Reynolds stress in different quadrants 由图7可见: (1)粒间区R的沿程分布接近水平线,第1、3象限及第2、4象限的分布曲线基本重合,第2、4象限的R总体大于第1、3象限,在总雷诺应力中占主导地位。 (2)颗粒区R的沿程分布呈“∪”状,各象限的R先减小后增大,在x+= 0附近取得最小值。 (3)粒间区R随颗粒间距及直径的变化较小,各工况第1、3象限R的沿程平均值分别为0.787、0.832和0.794,第2、4象限R的沿程平均值分别为1.755、1.788和1.562。在其他参数不变的情况下,增大颗粒间距或直径,均可使颗粒区R的差异减小,颗粒较大的工况3尤为明显,此时第1、3象限及第2、4象限R的沿程平均值分别为0.566和0.919,差值0.353,较前2种工况的0.759和0.634更小。 (4)粒间区各象限R值随工况的变化均小于颗粒区,沿程分布接近水平线,不同工况R的分布曲线也较接近。 (5)颗粒区各象限R值与颗粒间距和大小关系密切,工况1~3的R值依次减小,说明颗粒间距和直径越大,R值越小。 各象限紊动能的垂线平均值沿程变化见图8,分析显示: (1)E的沿程变化与R较为相似,粒间区E的沿程分布接近水平线,第4象限E最大,第2象限E次之,第3象限E最小,第2、4象限的紊动能总体大于第1、3象限,在总紊动能中占据主要地位,与钟强等[16]关于光滑床面明渠紊流的研究结论一致。 (2)颗粒区E的沿程分布也呈“∪”状,颗粒间距和直径越大,该分布趋势越明显,各象限的E先减小后增大,但在x+= 0附近波动较为明显。 (3)粒间区E随颗粒间距和直径的变化较小,以第2、4象限为例,各工况第2象限E的沿程平均值分别为1.365、1.460和1.155,第4象限E的沿程平均值分别为1.417、1.581和1.307。在其他参数不变的情况下,增大颗粒间距或直径,也可使颗粒区E的差异减小,颗粒较大的工况3尤为明显,该工况第2、4象限E的沿程平均值分别为0.872和0.840,相差0.032,均小于前2种工况的0.149和0.143。 (4)各象限E值与颗粒间距和大小关系密切,工况1~3的E值总体依次减小,说明颗粒间距和直径越大,E值越小。 (5)综合前文的分析,粒间区R、E沿程变化平缓稳定,而颗粒区R、E沿程变化具有明显的波动起伏,由此可以认为,床面采用梅花形排列方式加糙后,将改变R、E的沿程分布特征,调整颗粒区和粒间区的紊动能分布,从而形成局部加糙效应。 图8 各象限紊动能垂线平均值的沿程变化Fig. 8 Longitudinal variation of vertical average turbulence kinetic energy in different quadrants 2.3.2 总紊动参数 试验结果显示,各工况颗粒顶部以下区域总紊动参数的沿程分布具有一定的相似性。限于篇幅,图9以工况2为例,给出了各垂线平均总紊动参数Tu、R和E的沿程分布。 图9 紊动参数垂线平均值的沿程变化Fig. 9 Longitudinal varation of vertical average turbulence parameters 由图9可见: (1)Tu、R和E的沿程分布规律较为相似,且与象限紊动参数的分布趋势一致,具有明显的分区特性。粒间区Tu、R和E的沿程变化相对平缓,而颗粒区Tu、R和E的沿程变化呈“∪”状,颗粒轴线上游各参数数值明显减小,颗粒轴线下游各参数数值骤然增大。 (2)从沿程统计平均角度考虑,粒间区Tu、R和E的算术平均值分别为1.990、0.749和2.483,颗粒区Tu、R和E的算术平均值分别为1.375、0.244和1.436,减幅分别为30.9%、67.4%和42.2%。 (3)颗粒区Tu、R和E呈“∪”状变化,主要与水流绕过颗粒时的“收缩→扩散”过程有关。在颗粒轴线上游,水流呈逐渐收缩状态,紊动受到抑制。而在颗粒轴线下游,水流呈逐渐扩散状态,紊动得以恢复。 (1)颗粒顶部以上区域的纵向紊动强度Tu、雷诺应力R、紊动能E沿程基本呈条带状变化,受颗粒影响较小,而颗粒顶部以下区域的Tu、R、E受颗粒影响明显,沿程变化相对复杂,表现出一定的周期性和分区性,并可分为颗粒区和粒间区,各区Tu、R、E差异明显,且受颗粒直径d和纵向间距Lx等因素的影响。 (2)受颗粒阻水绕流、水流动量和能量重新调整分配的影响,颗粒区Tu、R、E的垂线分布在颗粒顶部以下区域波动明显,分布曲线呈“S”和倒“L”等形状。 (3)粒间区各象限的R、E沿程变化较为平缓,接近水平线,第2、4象限的R、E总体大于第1、3象限,颗粒区各象限的R、E沿程分布呈“∪”状并在沿程位置参数x+= 0附近有最小值。总紊动参数的沿程分布规律较为相似,且与象限紊动参数的分布趋势一致,具有明显的分区特性。 (4)本文研究主要针对雷诺数较小的二维水流,床面粗糙单元按梅花形阵列,今后可进一步探讨三维水流情况,分析颗粒排列方式、底坡、雷诺数等对紊流特性参数分布规律的影响,以丰富相关研究成果。
1.2 分析方法
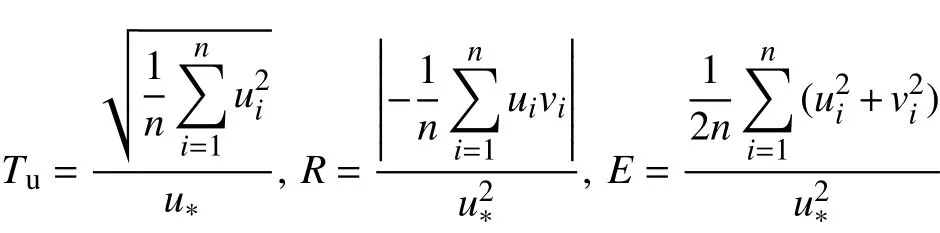

2 结果分析
2.1 紊动参数的云图分布

2.2 紊动参数的垂线分布
2.3 紊动参数特征值的沿程分布
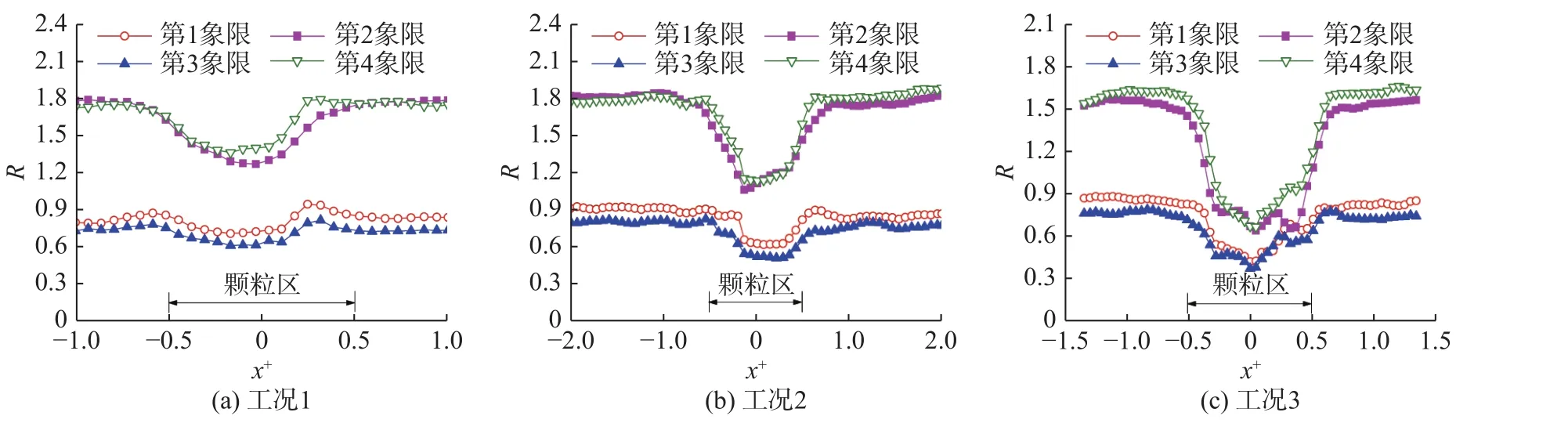
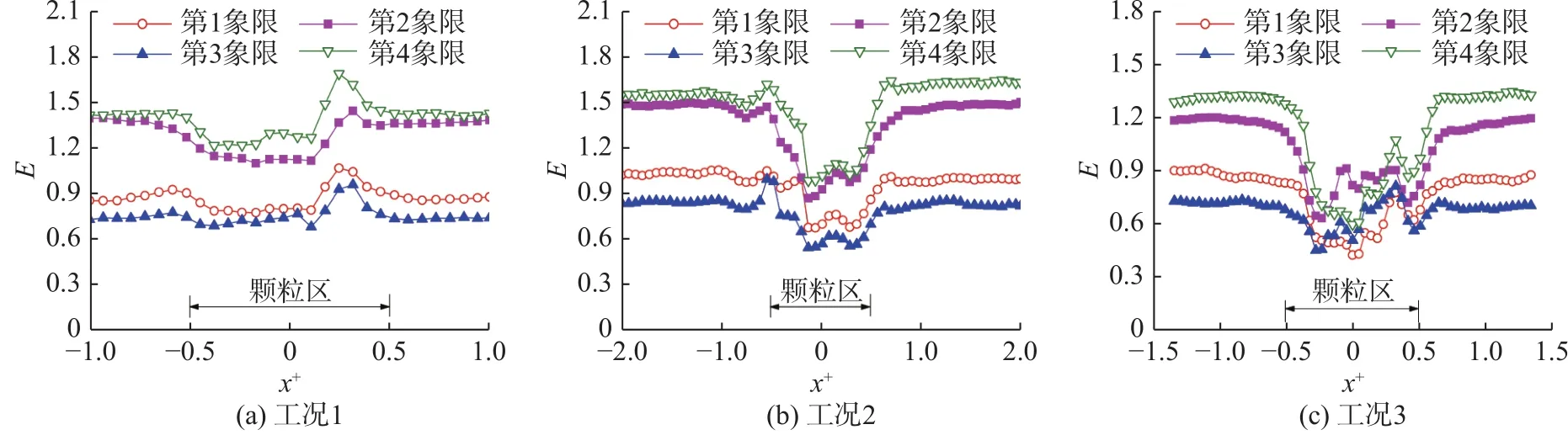
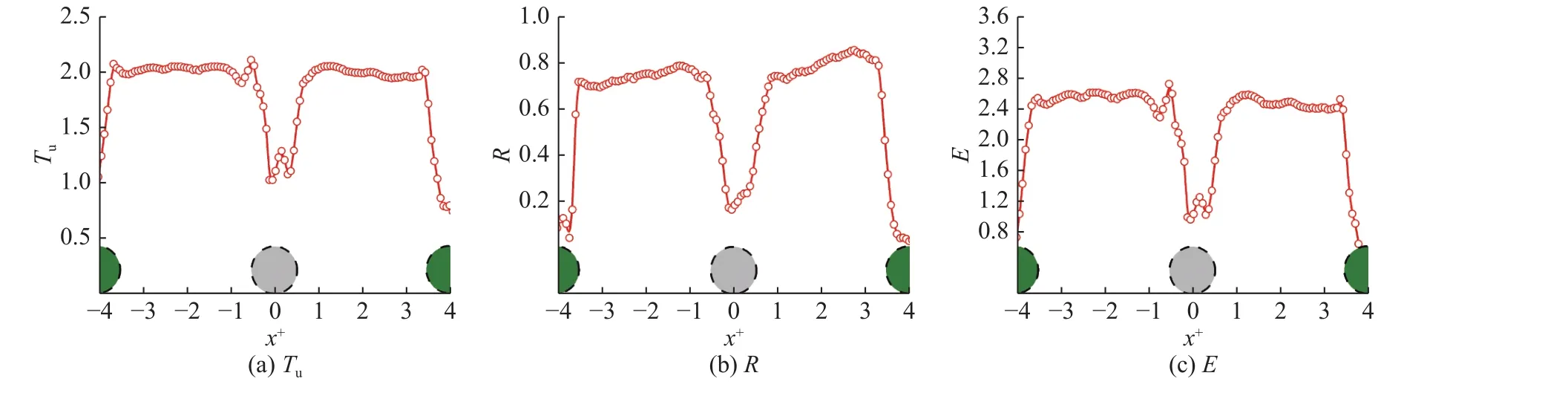
3 结 语
——以鄂东临兴神府地区为例

