粒间滚动阻力对砂土压缩特性影响的离散元模拟研究
沈 晨 鹏
(北京城建设计发展集团股份有限公司 轨道院第三设计所, 北京 100034)
在当代工程建设中,以北京市平原区为例,土层结构以砂卵砾石、砂土等土层结构为主,密集建筑荷载促进了局部地面沉降,虽然较上海软土地区沉降稍小,但由于高密度住宅及商业区的发展,仍出现了地表塌陷、沉降等问题,破坏了市政管线,引起建筑物的地基下沉,也有导致轨道交通工程发生不均匀沉降的风险,同时,砂土相较于其他土质更易产生液化现象,因此,在地下工程领域内,研究砂土的特性是必要的。
自然界中的砂土颗粒是形状不规则的,各向异性的,虽然已有大量文献总结砂土力学性能,但试验结果和理论研究总有一些局限性,室内试验仅能得到部分位置应力与应变,无法描述整个试样全部颗粒的变化状态。自离散元方法[1]被提出后,为研究土颗粒微观力学特性提供了重要的研究手段,基于离散元开发的数值软件也层出不穷。
数值模拟研究砂土力学性能的困难之一便是不能准确的模拟实际砂土的形状,因而大量的文献使用圆形颗粒并通过设置颗粒间的摩擦来反映颗粒形状间的阻碍摩擦作用,通过颗粒间的滑动来定义颗粒间粘结的断裂[2]。然而,1982年Oda等[3]通过试验研究发现,影响颗粒之间力学效应的主要是颗粒自身的转动而不是颗粒之间的滑动。为了改善这种现象,许多学者通过圆形颗粒引入粒间滚动阻力[4-7]来限制颗粒间的自由转动进而模拟颗粒形状对砂土力学性能的影响。如孙珊珊等[8]通过切割单个刚性球颗粒表面的试验,分析了颗粒表面粗糙度和不规则性的影响,提出增加颗粒表面粗糙度会使颗粒更易滚动,增加颗粒形状的不规则性会使颗粒更易滑动。Zhao等[9]讨论了粒间滚动阻力对结构演化和各向异性的影响,推断出滚动阻力模型能够模拟表面粗糙度较高颗粒的剪切强度,但需要依靠增加粒间滚动阻力来实现。Zhou等[10]通过改变两个圆形颗粒重叠间距的方式来生成不同形状的颗粒,对比结果后发现滚动阻力能从一定程度上反映颗粒形状对土体剪切峰值强度的影响,但当颗粒变得细长时,土样压缩性增强,不能通过增加粒间滚动阻力来反映颗粒形状的影响。Yang等[11]分别针对松砂和密砂中的圆形、椭圆形和三角形颗粒,分析了粒间滚动阻力与颗粒形状对土体剪切强度、固体分数、各向异性和接触力概率分布的影响,发现颗粒形状和粒间滚动阻力对土体各向异性的影响不同,不规则颗粒表面的摩擦效果要高于滚动阻力的影响。
综上所述,目前通过圆形颗粒引入粒间滚动阻力的方法不能准确反映不规则颗粒形状的效应,而且不同的滚动阻力模型和不同的计算方法得出的结论不一致,因而有必要进一步研究粒间滚动阻力的作用机制。以离散元颗粒流软件PFC2D为平台,采用其自定义的FISH语言,编制了考虑粒间滚动阻力的二维双轴压缩试验程序,研究了粒间滚动阻力对饱和松砂和密砂宏观和微观力学性能的影响。
1 考虑粒间滚动阻力的土颗粒运动方程
在研究土颗粒之间的接触力时,通常是将土颗粒间接触力在法向、切向和滚动方向三个方向进行分解,再分别针对这三种力学效应进行计算[12]。颗粒间的法向接触力会引起颗粒的平动,而切向接触力会造成颗粒之间的平动与转动。当颗粒的切向接触力达到颗粒间的滑动摩擦力后,颗粒粘结位置便会发生滑动破坏,破坏准则[13]为:
|Fs|≥μsFn
(1)
Fn=knxn
(2)
ΔFs=ksΔxs
(3)
式中:Fn为颗粒间的法向接触力;ΔFs为颗粒间的切向接触力增量;μs为滑动摩擦系数;xn为颗粒间的法向相对位移;Δxs为颗粒间的切向相对位移;kn为颗粒间接触力的法向刚度;ks为颗粒间接触的切向刚度。
颗粒的转动方程[14]为:
(4)
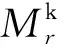
2 数值试验与结果分析
2.1 土样制备过程与试验过程
为了探究粒间滚动阻力对土体宏观和微观力学特性的影响,首先针对圆形颗粒建立了考虑粒间滚动阻力的力学模型。
土体双轴压缩试验所建立的计算模型尺寸为20 mm×40 mm,土颗粒的粒径范围为2 mm~6 mm,最终生成的土颗粒数量约为4 962个,土颗粒密度为2 650 kg/m3,初始孔隙率为0.15,颗粒间的接触模型采用 Rolling Resistance Linear Model,颗粒间的法向刚度与切向刚度之比为1,粒间滑动摩擦系数为0.5且始终保持不变,粒间的初始滚动摩擦系数设为0。在圆形颗粒土样的制备过程中,为了保证土样处于相同的试验条件,不同计算工况下土颗粒所有的参数保持相同且始终不变,土体颗粒的其它细观参数如表1所示。
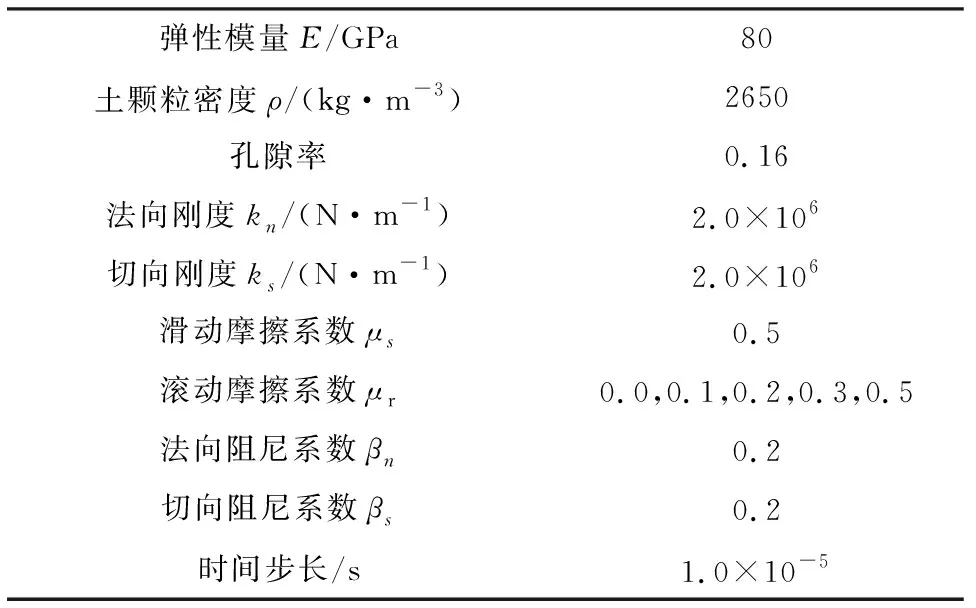
表1 模型试验参数
土样制备完成后,开始进行双轴压缩试验。首先将土样在应力控制方式下进行等向固结,直到土体颗粒间的接触力分布均匀且围压达到100 kPa。再保持水平向墙体应力值100 kPa始终不变,赋予顶墙和底墙以恒定速度相对移动;在剪切过程中采用应变控制方式控制上下墙的移动速率来实现对土体荷载的施加,在此过程中同时监测土体的偏应力、体应变等参数。这个过程即为近似模拟的土体双轴压缩试验过程[16]。
2.2 粒间滚动阻力对土体力学特性影响
2.2.1 土体宏观力学性能分析
在土体双轴压缩试验的过程中,由于土体在竖直方向与水平方向所受的压力不同而产生了应力差,该应力差称为偏应力。土体的偏应力是反应土体受力状态以及土体强度的一个重要指标,针对圆形颗粒在引入粒间滚动阻力后,计算了不同的滚动摩擦系数(μr=0.0, 0.1,0.2,0.3和0.5)下松砂、密砂的偏应力随土体轴应变的变化,结果如图1、图2所示,双轴压缩试验中密砂呈现出先剪缩后剪胀的规律,松砂为一直减缩的特性。密砂与松砂最终偏应力强度趋于相同。

图1 松砂密砂偏应力变化曲线

图2 松砂密砂体应变变化曲线
图3可以看出,在加载初期,密砂颗粒间的滚动摩擦系数对土体的偏应力影响较小;但随着轴应变的增加,土体偏应力呈现先增大后减小最终趋于稳定的变化趋势。同时,粒间滚动摩擦的存在使土体的偏应力峰值强度和残余强度都有所提高,且滚动摩擦系数越大,偏应力峰值就越大,所对应的轴应变也越大。图4显示密砂的体应变先减小后增大,及对应于砂土先剪缩后剪胀特性,滚动摩擦系数越大,密砂剪缩和剪胀的程度就越大。

图3 密砂偏应力随轴应变的变化曲线
同理,滚动摩擦系数对松砂偏应力的影响规律与密砂类似(见图5),但对体应变的影响不同。图6松砂不考虑颗粒滚动时,体应变随轴应变的增加一直减小直到平衡,及对应于松砂一直处于剪缩状态,但考虑粒间滚动后,松砂也出现了先剪缩后剪胀的特性,且滚动摩擦系数对松砂的影响显著。
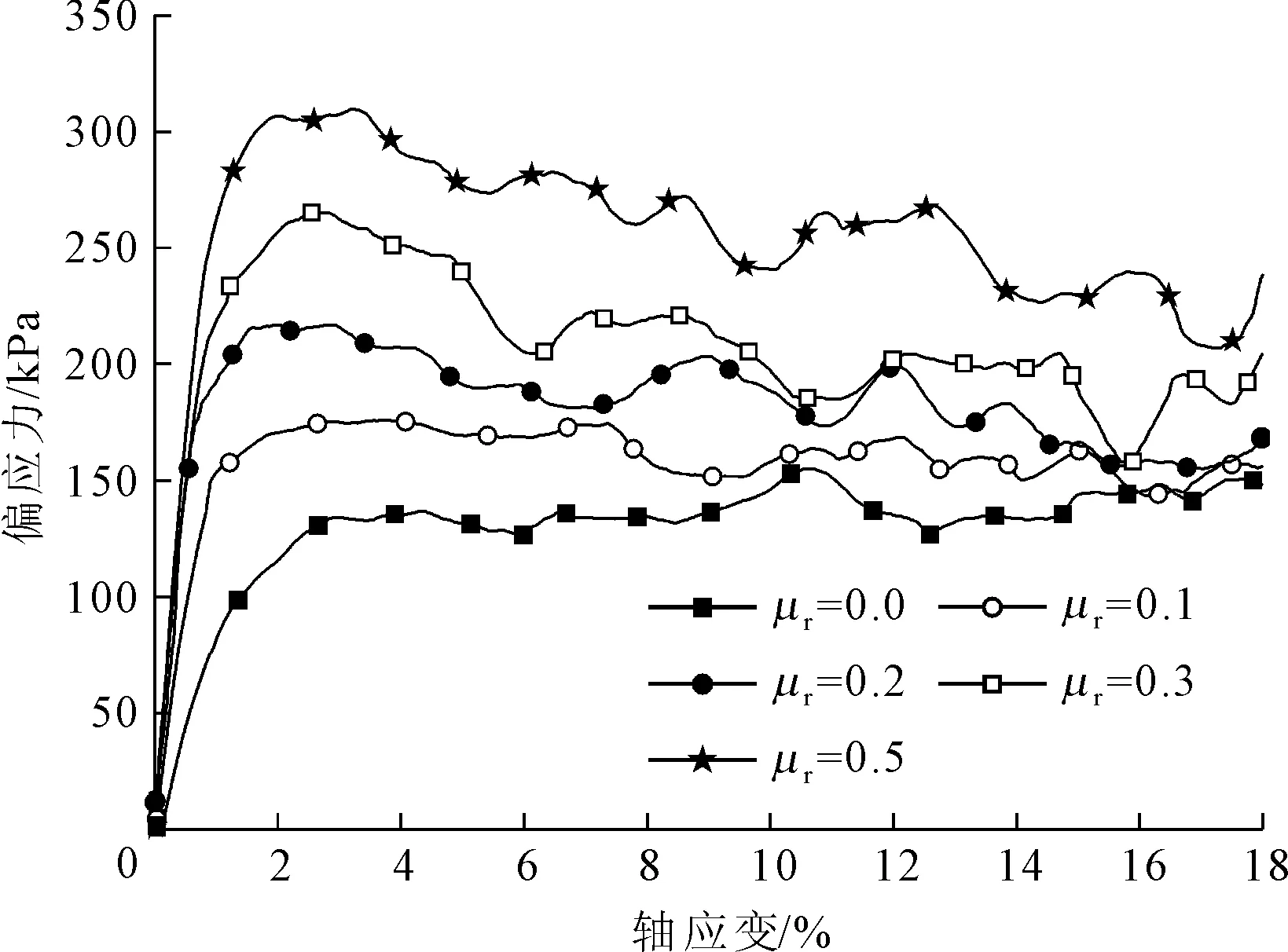
图5 松砂偏应力随轴应变的变化曲线

图6 松砂体应变随轴应变的变化曲线
2.2.2 土体微观力学性能分析
在分析粒间滚动阻力对颗粒的转动状态、土体力链的影响时,以密砂不考虑粒间滚动阻力(μr=0.0)和考虑粒间滚动阻力(μr=0.3)为例进行研究。图7是土体在双轴压缩试验结束后土颗粒转动角度的统计分布图(μr=0.0)。由图中结果可知,随着轴应变的增加,对角线处的颗粒转动角度最大,颗粒转动角度大于30°的颗粒数量也越来越多,且两条对角处颗粒转动方向相反。对比图7和图8可知,当密砂考虑粒间滚动阻力后,试样对角线处颗粒转动角度大约30°的颗粒分布范围较窄,这说明考虑颗粒转动效应后,颗粒的转动受到抑制。

图7 不考虑粒间滚动阻力的密砂土颗粒转动角度分布图
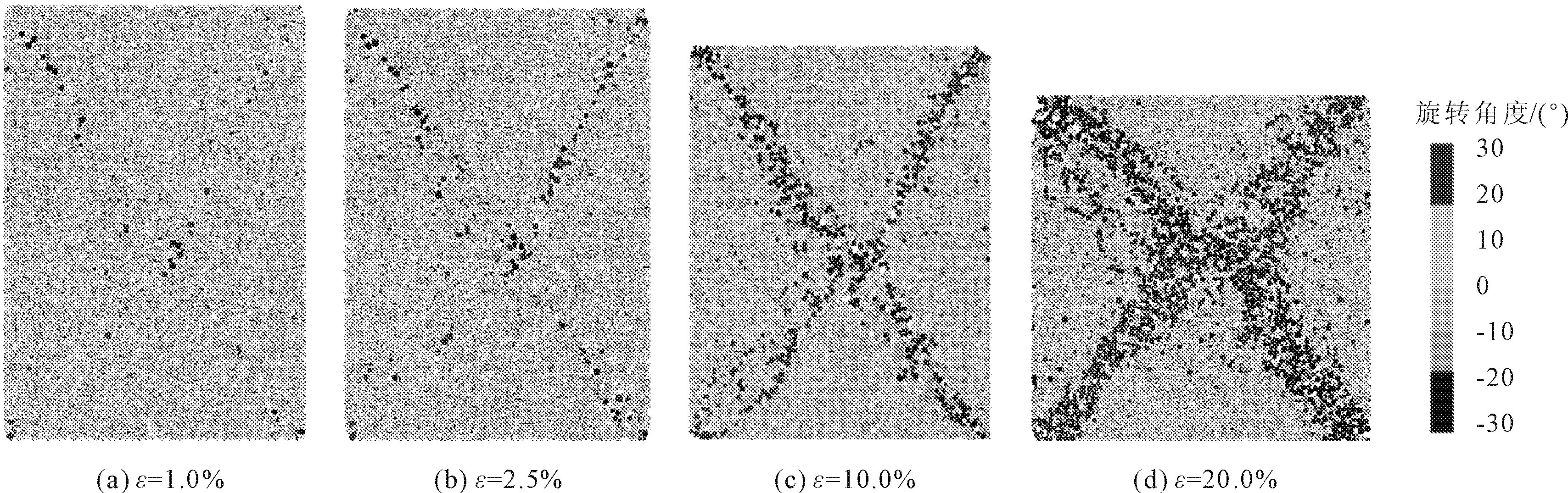
图8 考虑粒间滚动阻力(μr=0.3)的密砂土颗粒转动角度分布图
粒间接触力的分布可以用力链来表示,力链是传递土颗粒与土颗粒之间作用力的媒介[17],错综交错的力链构成了土体内部的结构骨架,控制着土体的稳定性,力链的失稳是导致土体崩塌的主要原因[18]。力链体现了土体内部土颗粒之间的作用力在某一时刻的状态,力链越粗,代表粒间接触力越大。图9(不考虑粒间滚动阻力)和图10(考虑粒间滚动阻力)是双轴压缩试验过程中土体内部力链的统计分布图。随着轴向应变的增大,土体力链粗细分布越明显,粗力链越来越多,即表示颗粒间接触力越来越大,土体受到剪切破坏时所需要的外界作用力越大。对比图9和图10可得,当土颗粒考虑粒间滚动阻力后,土体力链分布粗细较明显,说明粒间滚动阻力对土体力链的形成与分布有影响,即粒间滚动阻力的存在影响粒间接触力的数值大小与分布状态,力链分布形状更趋于树根状,且力链分布方向平行于试验加载方向。

图9 不考虑粒间滚动阻力的密砂力链分布图
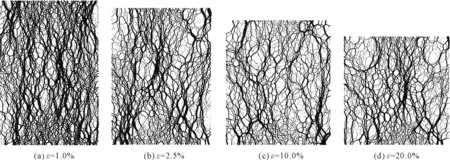
图10 考虑粒间滚动阻力μr=0.3的密砂力链分布图
3 结 论
依托离散元颗粒流软件PFC2D平台,通过土体的双轴压缩试验,研究了粒间滚动阻力对土体宏观和微观力学性能的影响,并总结了粒间滚动阻力对密砂松砂剪胀剪缩性质,分析了粒间滚动阻力对土颗粒转动状态和土体力链的影响,对砂土地层有一定的工程意义。得到的具体结论如下:
(1) 粒间滚动阻力会提高密砂、松砂的偏应力峰值强度和稳定强度,且滚动摩擦系数越大,偏应力峰值就越大。
(2) 密砂呈现先剪缩后剪胀的特性,滚动摩擦系数越大,密砂剪缩和剪胀的程度就越大。
松砂不考虑颗粒滚动时,松砂一直处于剪缩状态,但考虑粒间滚动后,松砂也出现了先剪缩后剪胀的特性,且滚动摩擦系数对松砂的影响程度显著。
(3) 相同轴向应变状态下,密砂考虑粒间滚动阻力后,对角线处转动角度大约30度的颗粒数量增加,分布较窄,土体力链粗细更分明。
——以鄂东临兴神府地区为例

