规则波对大直径群桩作用的数值模拟研究

干桂轩，孙 亮，岳 磊，韩松林

(1. 武汉理工大学 交通学院，湖北 武汉 430063；2. 大连理工大学 建设工程学部，辽宁 大连 116024；3. 长江科学院 水力学研究所，湖北 武汉 430010)

海洋平台的支撑结构往往由多根桩柱组成，当桩柱的直径和波长之比大于0.2时，它们被定义为大直径桩柱。由于水动力的相互影响，多个大直径桩柱表现出与单个桩柱不同的力学特性，即所谓的“群桩效应”。桩群在工作期间承受着较大的波浪荷载，它们的结构强度对于整个海洋平台的安全至关重要。因此，系统开展波浪与桩群相互作用的研究，对于准确评估海洋平台的安全性具有重要的工程意义。

国内外学者对波浪与桩柱作用已开展了一系列研究，Chakrabarti[1]通过模型试验在波浪水槽中测量了并排的两根桩、三根桩的波浪作用力系数与KC数 (Keulegan Carpenter number)和相对桩距的关系。高明道等[2]利用水槽试验研究了规则波作用下桩群受到的波浪力。杨正己等[3]利用水槽试验分别测定了规则波与不规则波作用在群桩上的波浪力。俞聿修等[4]通过试验研究了不规则波浪对小直径桩柱的作用力，在时域里分析了拖曳力系数CD、惯性力系数CM和KC数的关系，得出了群桩受力随KC数的变化规律。黄雯等[5]以某个群桩水动力模型试验为例，根据CFD理论建立了高桩承台和波浪水槽数值仿真的模型，分析桩间距及每个桩的位置对各桩受力的影响，总结了单桩和总力干扰系数的变化规律。Palma[6]和Zhang等[7]采用虚拟边界力法求解流体与结构物的相互作用。李玉成等[8]对波流共同作用下大尺度圆柱墩群周围的波流场进行了数值研究，得到大尺度圆柱墩群周围的波流场的耦合解。武昕竹等[9]基于Fluent平台建立了可用于波浪传播模拟的数值水槽，研究了聚焦波浪与结构物的相互作用。乔永亮等[10]运用流体力学分析软件ANSYS-CFX研究了3种湍流模拟方法对三维圆柱绕流数值模拟精度的影响，并分析了圆柱表面的受力情况。Sun等[11]使用三维水动力分析程序DIFFRACT和开源计算流体力学软件OpenFOAM对波浪与海上结构物相互作用进行了水动力分析。

虽然目前波浪与群桩柱作用的研究较多，大体可分为现场试验和数值模拟两类，主要是针对水动力系数和桩距的关系、波浪力的大小、波面升高和桩柱周流场的研究，关于群桩数量和布置方式对水动力特征影响的研究较少。本文拟采用基于势流理论开发的三维水动力分析程序DIFFRACT，系统研究大直径单个桩柱和群桩所受的波浪力与入射波频率之间的规律，以及桩柱间的相互作用对波浪力的影响，旨在为工程设计提供一定的参考。

1 控制方程及数值求解

流体在不可压缩、无黏、运动无旋的假定下，流场中存在速度势（图1），根据质量守恒定理，速度势满足拉普拉斯方程。对于波浪场中的固定式结构物，速度势可分解为入射势和绕射势：

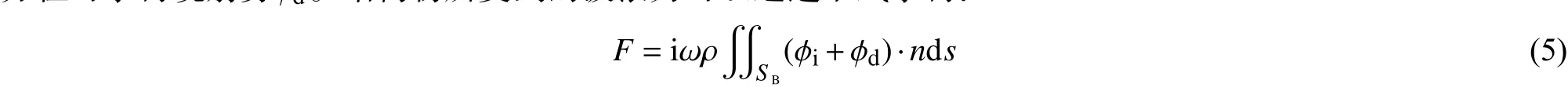
式中：ρ为水的密度。

2 波浪作用下单圆柱和双圆柱的受力验证分析

2.1 波浪对单圆柱的作用

为了与文献[13]中直立圆柱所受波浪力的解析解进行比较，将计算所得的波浪力除以ρgAπa2进行无量纲化处理。图1中取圆柱半径a=1.0 m，水深为d。当d/a=1和3时，单个直立圆柱上的无量纲波浪力如图2所示。如前文所述：大尺度和小尺度桩柱的划分标准为圆柱直径2a和波长L之比为0.2（对应ka=0.628，k=2)。图2中本文数值结果和文献解析解[13]在ka=0.1～3.0范围内都吻合较好，说明在忽略黏性影响的情况下，本文数值方法适用于小尺度和大尺度结构的分析。

2.2 波浪对双圆柱的作用

为了分析双圆柱所受的作用力，选取文献[14]中的例子。双圆柱的位置如图3所示，波浪从左侧沿x轴入射，计算中波高H=2A，波数k保持kH=0.2，圆柱半径a=1.0 m，两圆柱中心轴之间的距离s=3.0 m，水深d=3.0 m。

作用在双圆柱上的波浪力如图4所示，图4还包括文献[14]中的波浪力解析解和图2中单个圆柱（d/a=3）的无量纲波浪力。由图4的对比可以看到本文结果与文献结果吻合较好。图4的对比进一步验证了DIFFRACT在分析波浪与双圆柱的相互作用时具有很高的计算精度。

比较图4中两个圆柱所受到的波浪力可以发现：ka=0.5～2.5范围内作用在圆柱1上的波浪力都要大于作用在圆柱2上的波浪力。这是由于圆柱1处于迎浪侧，圆柱2处于背浪侧，圆柱1对圆柱2产生了遮蔽效应。更为重要的是，当ka=0.5～0.8时，双圆柱组中每个圆柱上的受力都要大于相同圆柱单独存在时的波浪力，说明两个圆柱的相互作用不可忽略。

图2 单个直立圆柱受到的无量纲波浪力Fig. 2 Wave loads on single vertical column

图3 规则波作用下的双圆柱Fig. 3 Twin columns in regular waves

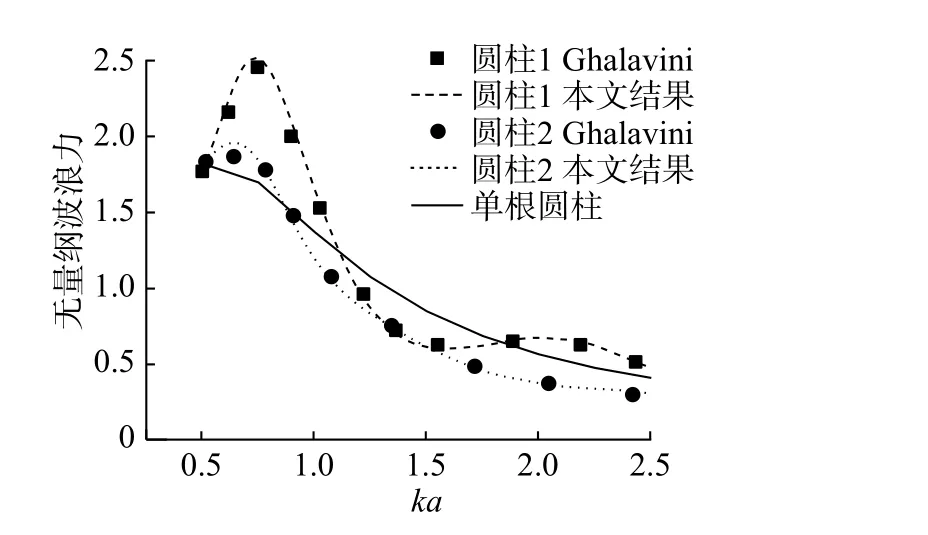
图4 作用在双圆柱上的无量纲波浪力Fig. 4 Dimensionless wave loads on twin columns

3 规则波对大直径群桩的作用

基于前文的验证，进一步研究波浪对4、5和6个圆柱所组成桩群的作用，各桩的位置及编号如图5所示。采用八节点高阶元，每个圆柱侧面单元数量为84个，环向21个，垂向4个。波浪依然从左侧沿x轴传播，计算中无量纲波数范围为ka=0.1～3.0。圆柱半径a=1.0 m，水深d/a=1，圆柱中心轴的间距为4.0 m。不同桩群中各个圆柱受到的单位波幅下的无量纲波浪力见图6～8，并与单根圆柱的结果进行了对比。

图5 桩群布置Fig. 5 Layout of column group

图6 （a），7（a）和8（a）分别为圆柱所受的无量纲波浪力。对于4圆柱组成的桩群，圆柱1的波浪力峰值最大，为1.53（图6（a））。波浪力峰值所对应的波浪频率有2个，并且大小相当。第1个峰值在单个圆柱时波浪力最大值所对应频率的附近。第2个峰值在ka≈1.66处，由圆柱之间的相互影响所造成。所以在群桩设计时，特征波浪参数的选取不能只参考单桩时的水动力特征，要充分考虑桩群中各桩的相互作用。对于5个圆柱组成的桩群，圆柱1的波浪力峰值为1.46（图7（a）），圆柱2和5的波浪力峰值最大，为2.00（图7（a））。因此，在群桩设计时不能只关注最前排迎浪的圆柱，应分析桩群中所有桩的受力。对于6圆柱组成的桩群，圆柱1的波浪力峰值最大，接近1.55（图8（a））。

图6 4圆柱结构受到的波浪力及群效应系数Fig. 6 Wave loads on four columns and coefficients of group effect

图7 5圆柱结构受到的波浪力及群效应系数Fig. 7 Wave loads on five columns and coefficients of group effect

图8 6圆柱结构受到的波浪力及群效应系数Fig. 8 Wave loads on six columns and coefficients of group effect

图6 （b），7（b）和8（b）分别为桩群中圆柱所受波浪力与单个圆柱时所受波浪力的比值，即群效应系数。由于多个圆柱的群桩作用，群效应系数的波动幅度很大。在很大频率范围内，群效应系数都大于1.0，说明桩群里每个桩所受的波浪力都大于单个桩时所受的波浪力。尤其是4个圆柱组成的桩群，圆柱1所受的波浪力在ka≈1.66处会达到单个圆柱时所受的波浪力的2.30倍（如图6（b）所示）。这说明群桩共振现象所引起的波浪荷载的增加在结构设计中是不可忽视的。

图9进一步比较了在4、5和6个圆柱组成的桩群中圆柱1所受的波浪力。如图9（a）所示，无论单个圆柱还是在桩群中，圆柱1受到的波浪力都在ka≈0.75附近出现峰值，所受的波浪力相差不大。对于4个圆柱组成的桩群，圆柱1受到的波浪力在ka≈1.66出现了另一个峰值，且与ka≈0.75附近的峰值相当。图9（b）中4圆柱桩群中圆柱1所受到的无量纲波浪力在ka≈1.66达到最大值2.30。

图9 桩群中圆柱1所受波浪力及群效应系数Fig. 9 Wave loads on column #1 in column group and coefficients of group effect

图6 ～9中多桩柱上波浪力的计算结果随ka发生激烈震荡，主要是由于多个桩柱之间的水动力相互作用。波浪力峰值对应的波数k与准共振频率相对应，发生准共振现象时，只有很少的波动能量能够从多柱结构之间传播过去，桩柱结构附近会出现非常大的波面升高[15]。

4 结 语

（1）单个直立圆柱所受的波浪力只有1个峰值，而桩群中每个圆柱所受到的波浪力存在多个峰值。4个圆柱所组成的桩群，迎浪的圆柱1受到的波浪力在所研究的频率范围内存在2个峰值，并且2个峰值的大小相当。因此，群桩设计时特征波浪参数的选取不能只参考单桩的水动力特征，要对不同的桩群进行分析。

（2）桩群中每个桩所受的波浪力往往大于单桩时的波浪力，群效应系数会随着桩的数量和布置的变化而变化。4圆柱桩群中迎浪的圆柱1所受波浪力的群效应系数在ka≈1.66达到最大值2.30。但对于5圆柱桩群，受力最大的是迎浪圆柱两侧的圆柱。因此，在群桩设计时不能只关注最前排迎浪的圆柱，应该分析桩群中所有圆柱的受力。

目前只研究了单一方向波浪作用下的群桩效用，后期研究中将考虑不同波浪入射时群桩中各桩所受波浪荷载的分布。本文的计算结果是基于势流理论得到的，没有考虑流体黏性的影响，所以计算所得的波浪力幅值在某些情况下可能会大于模型试验或现场的测量值。进一步的分析可以引入人工黏性项或者使用基于黏性流理论的求解器以得到更为精确的结果。