时空多特征流域场景模式库构建方法

巫义锐，汪浩航，魏大保，冯 钧

(河海大学计算机与信息学院，江苏 南京 211100)

如何提取水文数据间的非线性映射关系，准确高效地提供数据驱动模型的模拟结果，是人工智能技术在水文领域实例化的研究热点。然而，在实际应用中，原始水利数据的样本量往往不能满足人工智能模型的数据需求。因此，如何提高数据的精细化程度以扩充数据信息，提升人工智能模型的性能，成为智慧水利研究者关心的话题。

基于水文数据的时空本征特性，本文拟构建细粒度的时空场景，用以扩充数据信息。例如，水华管理主题中的污染因素复杂多样，包括氮、磷含量等，拟构建不同水华场景，重点监测该场景中导致水华发生的关键污染因素，总结数据特征，提取场景模式，提高水华预测的准确性。基于上述分析，本文将场景定义为表征流域典型变化趋势的关键要素数据集。步骤如下：(a)对原始数据进行事件化分割；(b)通过水利数据间关联关系建模，提取场景要素特征；(c)基于特征选择方法，提取关键特征以初始化场景；(d)场景聚类以提取场景模式，构建高效的场景模式库。

1 场景模式库相关工作

水利大数据多为时序数据，本文通过时序分割、时序特征提取、时序聚类技术构建时空场景模式库。以下主要介绍这3项技术的相关工作。

a. 多元时间序列分割技术。该技术具有数据结构多变、各元数据之间关系错综复杂、计算量大等特点。多元时间序列分割方法可分为基于模糊聚类与基于动态规划的多元时间序列分割。Wang等[1]提出了基于Gath-Geva聚类算法的多元时间序列分割方法，将数据时间信息作为额外的变量加以考虑，并引入最小信息长度原则，实现了精准的多时序分割。Guo等[2]利用动态规划算法，提高分割断点的查询速度，减少了多元时序分割计算的时间复杂度。Bankó 等[3]基于阈值自回归模型，实现了多变量时间序列的同步分割，并将其应用于水文气象数据集。

b. 时序特征提取技术。该技术可分为基本统计方法和基于变换的特征提取技术。前者提取统计特征来表征原有时序数据，常见的时域统计特征值有均值、方差、极值、过零点、边界点等[4]，频域统计特征值包括功率谱、功率密度比、中值频率、平均功率频率等。后者则意图强调适合任务的特性部分，可分为时频、线性、模型变换。时频变换包括快速傅立叶变换、短时傅立叶变换、倒谱系数等，线性变换包括PCA、线性判别式分析等。模型变换使用智能算法描述时间序列本征特征，进而提取模型系数为特征向量。例如对于水文领域的平稳时间序列，研究者常使用ARMA模型(自回归滑动平均模型)及滑动平均模型(MA)或组合-ARMA模型等进行拟合[5]。

c. 时序聚类技术。该技术可分为3类，分别为基于原始数据、基于特征和基于模型的时间序列聚类算法。第一类方法直接将传统的聚类算法应用于时间序列数据。基于K-means聚类方法，Huang等[6]使用DTW距离度量方式对时间序列的平滑子空间进行聚类。第二类方法先从原始序列中提取具有代表性的特征，再通过聚类算法对特征序列进行聚类分析。嵇敏等[7]通过正交函数将高维时间序列转换到低维空间，并结合函数度量实现模糊C均值聚类，其中C指聚类中心个数。第三类方法可大致分为2种方法[8]：统计学习方法(如ARMA)[9]和人工神经网络方法(如SOM)[10]。该类方法能够挖掘时间序列数据的随机性以及潜在的数据规律，但算法建模复杂，计算量大。

2 场景模式库构建方法

构建场景模式库的技术路线如图1所示。首先通过多元时序分割技术，从原始时序数据中提取出相关的多元时序数据，并挖掘各元数据间的相关性，形成场景要素数据。场景要素定义为组成场景的数据类型集合。由于多元时序场景数据难以计算，使用混合特征提取技术提取时空特征，实现信息降维和增强。最后，对时空特征数据进行聚类，构建场景模式库。

图1 时空多特征流域场景模式库构建技术路线Fig.1 Technical route of watershed scene pattern library construction via spatio-temporal multiple features

2.1 多元时序异步分割技术

多元时序分割技术的目的是从原始时序数据中提取出相关事件的多元时序数据。如某站点发生了一次水质富营养化事件，由于水质富营养化事件的复杂性，各元数据变化会呈现异步发生规律。基于水利事件的异步特征，该技术首先对各元数据进行一元时序分割，获取具有事件特征的各元分割数据；而后使用距离度量公式依次度量各二元分割数据，从中关联相似和相关的分割数据，划分分割组；最后合并具有交集的分割组，获取多元时序异步分割数据。将多元时序序列定义为

(1)

式中：X——某站点所测的多元时序数据；xi——第i个属性对应的时序数据。

2.1.1 一元时序分割

定义一元时序数据的分割结果如下：

S(xi)={si,k|k∈[1,l(xi)]}

(2)

其中si,k=

式中：S(xi)——第i个属性时序数据分割，结果是一个分割段集合；si,k——第i个属性时序数据中的第k个分割段；l(xi)——第i个属性时序数据分割数目；l(k)——第k时序段中间数据的位置；w——时序分割段的长度。如算法一所示，采用极值点方式，提取一元时序分割段。该算法中，len(xi)表示xi所代表时序数据的长度。所提取特征点的值需为极值，且大于阈值。

算法一一元时序分割。 输入：一元时序数据xi阈值:threshold；输出：S(xi)。步骤如下：

Result={}

k=1

forj=1 to len(xi)do

ifxi,j>threshold andxi,j>xi,j-1andxi,j>xi,j+1do//寻找特征点

l(k)=j

Result.append(si,k)//存储含有特征点的分割段

k++

end if

end for

S(xi)← Result

[ResultS(xi)]

2.1.2 相似度量方式

时序数据之间度量方式主要分为2种：相关性和相似性[11-12]。相关性一般采用皮尔逊相关系数公式，相似性则采用DTW距离度量公式。皮尔逊相关系数只能度量线性相关性，同时要求所输入的数据维度相同。DTW距离公式可以度量非等长的时序数据，但是只能度量正相关时序数据间的距离，在负相关数据上，其度量性能较差。本文所处理的水文时序数据存在负相关，且输入维度不同，因此提出将两者相结合的新度量方式：

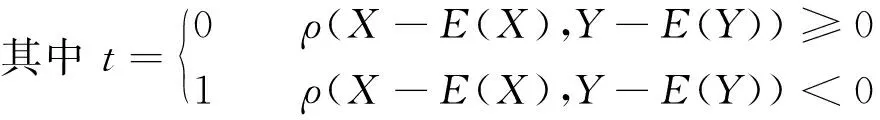
(3)

式中：E(·)——期望函数；ρ(·)——2个等长时序序列的相关性。

当输入数据呈正相关时，分子等价于直接使用DTW公式度量时序数据间的距离；当输入数据呈负相关时，在分子中，先将输入数据Y进行一次轴对称变换，将输入数据之间的负相关转变成正相关，然后使用DTW距离度量。在分母中，当输入数据越趋向于正相关和负相关时，分母的值就越大，距离值越小，相似性越大，分母加一的作用是防止分母出现为零的情况。

2.1.3 多元时序分割

如算法二所示，通过一元时序分割和改进的相似度量公式对多元时序数据进行分割。

算法二基于改进相关度量方式的多元异步时序分割。输入：多元原始时间序列X;输出：多元异步分割数据集MultiSegSet步骤如下：

SegSet={}

第一步：fori=1 to len(X)do //一元时序分割

SegSet[i]=S(xi)

end for

//利用度量公式获取相邻两元之间相似的分割数据集

第二步：fori=1 to len(X)-1 do

//分割数据集之间度量

SegCorr[i]=Correlation(SegSet[i],SegSet[i+1])

end for

//合并校正相邻两元的分割时序，组合成多元异步分割数据

第三步：fori=1 to len(X)-1 do

MultiseSet=MergeSeg(MultiSeg,SegCorr[i])

eng for

Return MultiSegSet

//挖掘两个分割数据集中的关联分割段

function Correlation(SegSet[i],SegSet[j])

Result={}

forxin SegSet[i] do//遍历第一个分割数据集

Min=inf;temp=null

foryin SegSet[j]do//遍历第二个分割数据集

if Uion(x,y)!=null and DTWCorr(x,y)do// 关联条件

//挖掘相似距离最小的分割段

Min=DTWCorr(x,y)

temp=y

end if

end for

Result. append() //将关联的分割段保存

end for

return Result

//MX→,MY→

function MergeSeg(MX,MY)//返回合并分割段

Result={}

//threshold = 0.5 合并条件，保持上下连接性

if Union(mxn,my1)>threshold do

Result.append()//保存结果

end if

return Result

算法二中，Correlation(·)函数功能为挖掘2个分割数据集中的关联分割段，其输入为2个一元时序分割集，输出是关联分割数据集。MergeSeg(·)函数合并具有相同分割段的关联分割段，最后得到多元时序分割数据，输入的第一个参数为已经进行多个关联分割数据集合并的结果，第二个参数为只含有2个分割数据集的关联分割段，其中mxi和myj为一元时序分割段，和si,k结构是相同的，在这里为了更方便叙述，因而使用新的符号进行代替。

2.2 混合特征提取技术

基于多元时序分割技术获取的不同场景，挖掘与构造场景数据特征[13]。综合2种特征提取方式构建混合特征提取。首先。采用傅里叶变换方式，将数据从时域空间变换到频域空间；然后，利用统计方法从频域幅度值中提取特征。选取均值、标准差、最大值、最小值、过零点数这5个特征数值用于统计特征构建。

(9)

式中：X(r) ——频率为r时的幅度值，因此X=。直接将幅度值序列作为特征，在计算过程中效率低下，因而采用时序统计特征方法对幅度值序列进行特征提取。

2.3 基于K-means聚类方法的场景模式库构建技术

通过时序特征提取技术，可以将各个站点各个时间区内的数据进行特征提取，大大减少了冗余数据，缩短数据的规模，有利于数据进行聚类[14]，挖掘其相似场景以及场景之间的相关性，从而构建场景模式库，由于目前提取的特征为数值本身特征，而忽略数据的时空信息，因而在聚类之前，进行时空特征提取，综合混合特征和时空特征，使用传统K-means算法[15]对数据进行聚类，构建时空场景模式库。

多特征时空场景模式库主要分为3个步骤:第一步,对样本中的场景数据进行混合特征提取;第二步，对场景数据进行时空特征提取；第三步，对特征数据进行归一化，使用K-means聚类算法对特征数据进行聚类，聚类后的特征数据所对应的场景数据为场景模式库。

算法三基于多特征的K-means聚类算法。输入：样本集MultiSegSet={MultiSeg1,MultiSeg2,…,MultiSegm}和聚类簇数k；输出：簇划分。步骤如下：

//对样本数据提取混合特征

MultiMixFeatureSet={MixFeature1,MixFeature2,…,MixFeaturem}

//对样本数据提取时空特征

STFeatureSet={STFeature1,STFeature2,…,STFeaturem}

//合并混合特征和时空特征并归一化

FeatureSet={Feature1,Feature2,…,Featurem}

从FeatureSet中随机选择k个样本作为初始均值向量(u1,u2,…,uk)

repeat

令Ci=Ø(1≤i≤k)

fori=1,2,…,mdo

//计算样本featurej与各均值向量ui(1≤i≤k)的距离(欧氏距离)：

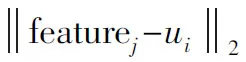
根据距离最近的均值向量确定featurej的簇标记：λj=argmini∈{1,2,…,k}dji

将样本xj划入相应的簇：Cλi=Cλi∪{featurej}

end for

fori=1,2,…,kdo

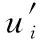
else

保持当前均值向量不变

end if

end for

Until当前均值向量均未更新

returnS={C1,C2,…,Ck}

3 水利数据集试验

3.1 试验说明

试验使用引江济太水量水质数据，该数据包含207个水质测站所测的数据。每个站点水质监测的场景要素数据为：水温、透明度、溶解氧(DO)、pH、电导率、化学需氧量(COD)、总磷(TP)、氨氮等，其中某些湖泊站点包含叶绿素浓度、浮游植物等指标。选择2008年贡湖水厂所监测的总氮(TN)、总磷以及透明度数据进行试验。

先用一元时序分割技术对各个场景要素数据进行一元分割，后使用滑动窗口对分割数据采样，防止数据存在缺失和冗余情况发生，再使用改进的相关度量方式度量各场景要素数据间关系，最后合并具有相关关系数据，实现多场景要素关联及多元时序分割。在本试验中，采用基于动态规划(MDS)的和基于Gath-Geva模糊聚类(MFS)的多元时序分割方法作对比试验。在基于动态规划的多元时序分割试验中，设置分割阶数为7。在基于模糊聚类的多元时序分割试验中，设置聚类个数为2。

3.2 试验结果

图2展示了人工分割多元时序的理想结果，其中TN、TP以及透明度数据的变化具有一定的滞后性。此外可发现分割段中的TN和TP具有一定相似性，透明度则和TN分割段成负相关关系。图3是本文使用的多元分割方法，可看到时序被分割成6段，且每段各元数据在不同时刻分割。该结果仍具有缺陷，例如在TP分割段中，第4、5和6段重合，与实际情况不符，该方法仍需要改进。图4是基于模糊分类的多元分割结果。分割段中各元数据都在同一时刻进行分割，但该方法将时序分割过多段数，存在分割段长度过小，如第5、6、7段，分割段过长，如第8、9段。同时无法发现分割段各元之间的明显关系。图5是基于动态规划的多元分割结果，主要分割成6段，其中某一段分割过小，在实际中舍去；从分割结果上看出，该方法依然存在基于模糊聚类的多元分割方法的缺陷。

图2 多元时序人工分割Fig.2 Experimental results of multivariate time series by manual segmentation method

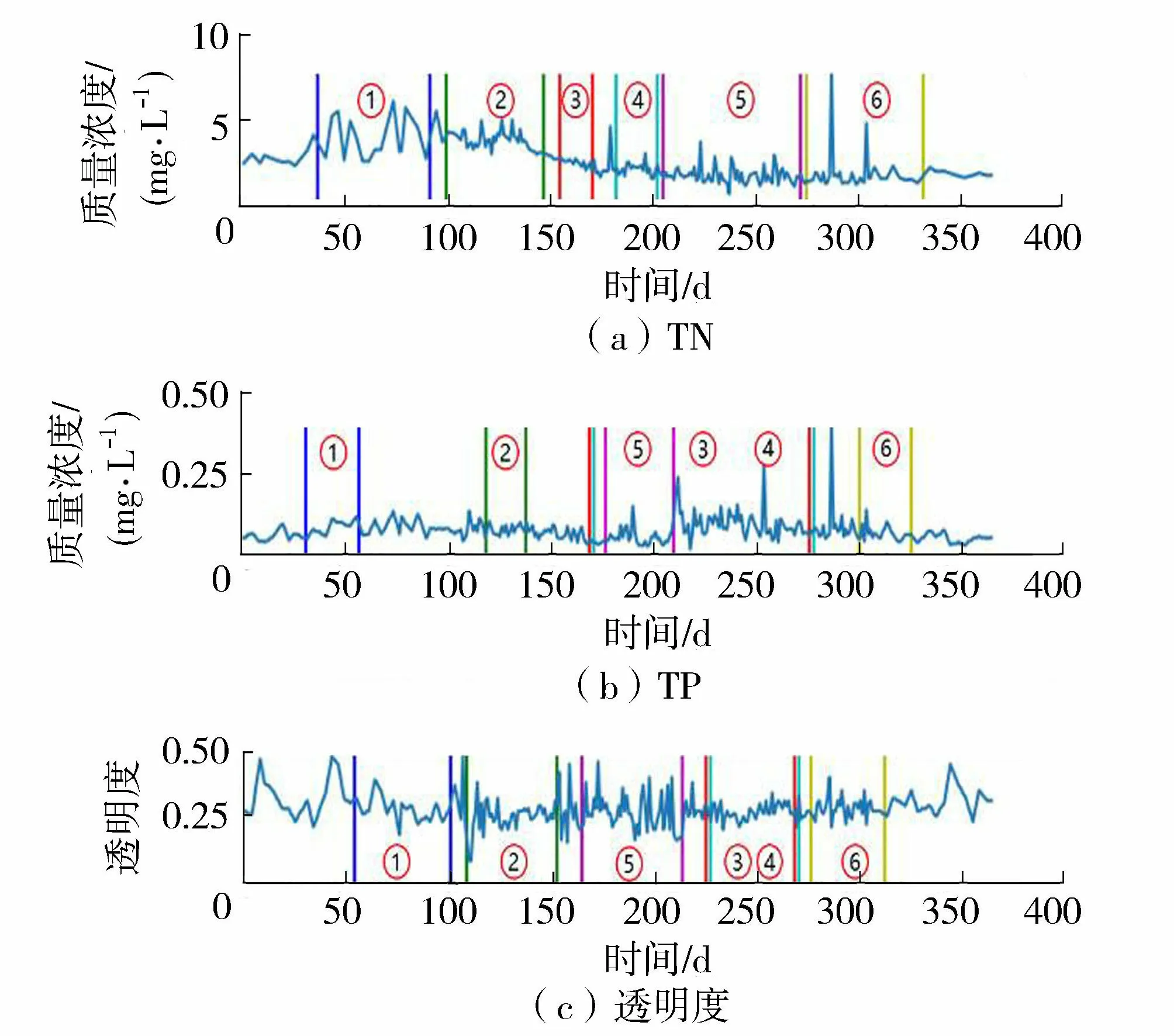
图3 基于本文所提方法的多元时序分割Fig.3 Experimental results of multivariate time series by proposed method

图4 基于Gath-Geva模糊聚类的多元时序分割Fig.4 Experimental results of multivariate time series by MFS

图5 基于动态规划方法的多元时序分割Fig.5 Experimental results of multivariate time series by MDS

3.3 试验结果分析

本文进行了所提方法、基于动态规划以及基于Gath-Geva模糊聚类多元时序分割方法对比试验。本文采用人工分割时序段作为标准分割段，采用交并比(IoU)评估试验结果。由于各试验分割段数不同，因而采用平均值的方式反映整体分割效果，如表1所示。

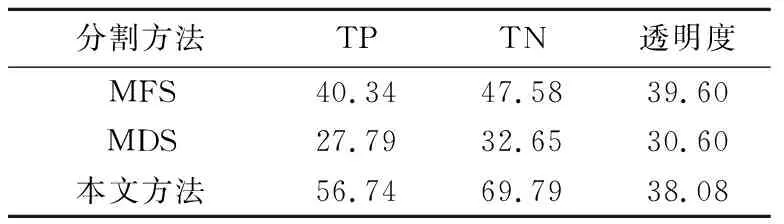
表1 3种多元时序分割方法评估结果Table 1 Evaluation results of three different segmentation methods for multivariate time series %

由表1可知，本文方法在TN和透明度方面明显优于其他2种分割方法，在TP方面比MFS方法差。其主要原因在于多个多元时序分割段在TP场景要素上发生时序段重合，这与标准分割段相差较远，大大降低了试验分割效果。从整体上看，所列3种分割方法的性能均待提升。MFS和MDS无法提供更加细粒度的分割时序段，其分割时序段过长，导致性能下降。同时，这两种方法都是同步分割，多元时序分割段的断点在同一时刻，与人工分割具有理念差异。本文所提方法在贡湖水厂2008年的3个场景数据上的分割效果优于其他2种方法，但仍需提高分割效果。

4 结 论

水利场景搭建是一个复杂的过程。通过分析太湖流域各站点数据以及引江济太工程调水数据，发现单时序分割技术具有其相应的局限性，进而利用多元时序分割技术对各站点数据进行关联分割，然后利用特征提取与选择技术构建时序水文特征，最后，从特征中挖掘出场景的规律。