循环荷载作用下海上风机单桩基础周围砂土沉降与对流特性

郑金海，丁星宇，管大为，李嘉隆

(1.河海大学海岸灾害及防护教育部重点实验室，江苏 南京 210098；2.河海大学港口海岸与近海工程学院，江苏 南京 210098)

海上风能因其利用率高、储备大、不占用陆地资源等特点备受青睐。目前已运行的海上风电场中，风机基础采用单桩基础的比例接近75%[1-2]，我国大部分海域也适合采用单桩基础作为风机基础形式[3]。海上风机在运行期不仅承受竖向荷载，还要承受更为复杂的水平向风、浪、流环境荷载[4-5]。风和浪的周期性决定了海上风机所受荷载具有循环荷载的特征。此外，海上风机受到的水平荷载还具有长期性，据统计，海上风机在其在役期间通常要承受106～108次循环荷载作用[6]。这些低频的循环荷载将造成桩基础的永久侧向变形，当桩身转角超过0.5°，可能造成风力发电机无法正常运作[7-8]。有研究发现，桩基础长期循环往复的水平位移会导致桩侧砂土颗粒产生局部沉陷和准静态流动[9]，这种颗粒的流动，会显著改变基础周围的土体物理特性(如密实度、孔隙水压力、刚度等)，还会显著改变桩周的局部冲刷进程[10]。因此，开展单桩及其周围砂土在长期循环荷载作用下的运动响应机制相关研究对风机安全运行具有重要意义。

水平循环荷载作用下单桩基础周围砂土沉降和流化研究是当前的研究热点问题。Brown等[11]指出桩周砂土沉陷现象主要源于振动对砂土产生了致密化作用，具体表现为：在循环荷载作用下，桩土界面间歇性地产生了空隙，进入桩-土空隙的砂土由于受到桩的反复挤压，被挤入其他颗粒的空隙之中，导致土体孔隙比减小，宏观上形成桩周土体的局部沉陷。Cuéllar等[9]发现水平循环荷载作用下的桩顶位移幅值逐渐减小，间接证明了桩周砂土在振动作用下的密实过程。Guan等[10]通过水槽试验对水平循环荷载作用下桩基周围砂土的沉降过程和密实度变化进行测量，发现沉陷坑深度随时间的增长趋势近似于指数函数。相对于桩周砂土的局部沉陷现象，水平循环荷载作用下桩周砂土颗粒产生的“流态化”运动更加难以观察并且机理更为复杂。王富强等[12]较早关注了桩周土体的运动，发现土体水平向和竖向变形均集中在一定范围内，但没有对土体变形进行系统深入的研究。Cuéllar等[13]进行了水平循环荷载作用下单桩和砂土相互作用的物理模型试验，通过在砂床表面设置彩色示踪砂的方法，猜测在床面以下靠近桩基的区域出现了颗粒的对流运动现象。为直观的记录桩周土颗粒的对流运动全过程，Li等[14]搭建了二维试验模型，研究了桩顶荷载幅值和加载频率对土体变形的影响，但其并未对对流的机制进行详细阐述。赵家林[15]和Zorzi等[16]开展了水平循环荷载下桩土相互作用二维模型试验，并借助PIV(particle image velocimetry)粒子图像测速技术对砂土颗粒运动的流动轨迹场进行了简单的量化，但由于其试验设计较为简单且测量分辨率较低，试验结果对桩周砂土沉降及对流运动时空演变特性并未给出较为细致的展示。

本文基于室内概化二维模型试验，深入研究水平循环荷载作用下桩土相互作用机理，对不同桩顶振动频率和振幅条件下桩周砂土运动过程进行模拟，量化桩基振动过程中桩身在土层中的变形、桩周砂土沉降以及砂土颗粒对流的演变特性，分析不同循环荷载频率及振幅下桩周砂土的运动响应机制。

1 室内模型试验

为清晰观察水平循环荷载作用下桩土相互作用过程，本研究搭建了一套室内概化二维模型试验系统，采用二维的桩基(长方体板)代替三维圆桩；将实际海况中的周期性风荷载、流荷载、叶片转动产生的循环动力荷载简化为统一作用在模型桩顶部的水平循环荷载，通过改变桩顶水平循环荷载位移幅值及频率模拟不同工况组次。本试验的装置主要包括试验砂箱、二维模型桩、循环荷载加载装置、图像采集设备和辅助照明设备。

1.1 试验砂箱和模型桩

试验砂箱是无顶面和前立面的四面长方体容器，其内部尺寸为55 cm×4 cm×45 cm(长×宽×高)。在砂箱底部中央有一对相对放置的角铁，角铁上各添加两个对称的螺纹，用以固定模型桩。砂箱的一侧焊接了金属架，用以固定电机和传动装置。试验采用的模型桩尺寸为1 cm×4 cm×70 cm(厚×宽×高)，材质为铝合金，密度为2.75 g/cm3，弹性模量为68.9 GPa，入土深度为30 cm。试验时，模型桩竖直放置在砂箱中央两块角铁之间，用两侧的螺钉固定底端，以保证振动时其运动的二维性。砂箱正面夹持一块钢化玻璃，在模型桩靠近钢化玻璃的一侧有橡胶薄膜覆盖，以防止试验过程中有砂粒进入模型桩和钢化玻璃之间，导致玻璃磨损影响观测。试验装置布置如图1所示。

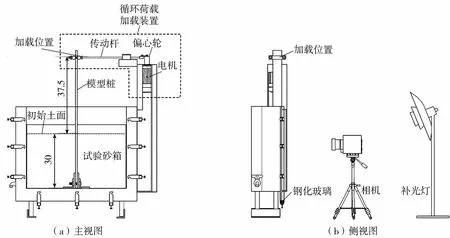
图1 试验装置布置(单位：cm)Fig.1 Sketch of the experimental set up(units:cm)

1.2 循环荷载加载装置

试验的循环荷载加载装置由大力矩电机、调速器、一组偏心轮、复合传动杆及固定槽组成，能够在距土面37.5 cm位置处持续施加正弦形水平往复位移。电机的功率为90 W，配合调速器，转速可以在0～300 r/min之间任意调节，以控制加载频率。试验的偏心轮采用数控机床加工，与电机连接的一端在中心打孔，另一端打孔位置偏离圆心，复合传动杆中连接有压力传感器，穿过固定槽以保证传动杆的水平和压力传感器所受力为水平力，复合传动杆可以调节自身长度，通过由2根细圆柱组成的夹持装置与二维模型桩连接，以保证模型桩初始位置为中立位。经过率定，电机输出的循环荷载频率误差为±0.2 Hz，配合偏心轮可以输出的位移幅值为0.42 mm、1.42 mm、2.06 mm、2.33 mm。

1.3 试验用砂

本试验采用质量-体积法将不同颜色的砂分层填入砂箱，即每层(2 cm)采用固定质量的土填入，再用工具整平压实，以保证砂箱内砂土密度均匀。为便于展现土体变形过程，自下而上分别铺填有混合砂、黑砂、绿砂、红黄混合砂、蓝色示踪砂。试验铺填方式如图2所示。同时根据GB/T 50123—2019《土工试验方法标准》进行颗粒分析试验、比重试验、相对密度试验等，得到试验用砂的各项指标如下：相对密度为2.69，中值粒径D50=0.48 mm，不均匀系数为1.06，最大干密度为1.723 g/cm3，最小干密度为1.379 g/cm3，最大孔隙率为0.951，最小孔隙率为0.561，密实度为0.308。

图2 试验填砂方式 Fig.2 Sand filling method

1.4 图像采集设备

图像采集设备由单反相机和高速摄像机组成，用于不同阶段的拍摄。单反相机为SONYA57，采用的分辨率为3 568×2 368像素；高速摄像机为FASTCAM Mini WX50，摄像的最高帧率为67 500 fps，试验中采取的分辨率为2 048×2 048像素，帧率为500 fps。

1.5 数据处理方法

试验数据主要为数字图像，针对不同的研究问题，采用不同的处理方法。本文主要使用了在图像上点取相应特征点的像素坐标计算出特征长度的像素数量，并根据单位长度的像素数量将其转化为长度的方法，以及PIV和PTV方法。

1.5.1 PIV方法

PIV粒子图像测速法是一种基于图像处理技术和互相关算法的试验测速方法[17]，相对于其他测量流体流速的方法，PIV技术具有非接触式测量和较高的测量精度等优点。近年来PIV技术被广泛应用于岩土工程领域，涉及土体变形和颗粒运动[18]，观察土体和岩石的内部空隙结构[19]等。传统PIV算法通常是对单时间步长Δt的2张照片进行互相关运算而得到速度场，在此过程中，因为图像序列数据均是离散化的，因此在检测窗口中的互相关值只能对应整数倍的像素变化，即当存在只有半个像素的变化时，计算得到的位移存在一定误差。这种位移上的偏误差通常是随着像素间隔周期性变化的，被称作是峰值锁定效应[20]。针对传统PIV方法中单时间步长求解算法的缺陷，Hsieh等[20]和Guan等[21]提出了一种具有较高时间分辨率的多时间步长求解算法，用以克服前文提到的误差。本试验在振动达到72 h时，使用单反相机以5 s/张的速度对桩周附近砂土拍摄2 000张以上照片用于记录桩周砂土对流过程，由于本文所研究的桩周砂土运动速度梯度变化较大，为避免出现上述峰值锁定效应，用多时间步长求解算法对砂土对流流场进行计算，计算最小空间分辨率为8像素(0.5 mm)。

1.5.2 PTV方法

PTV粒子追踪测速法是通过追踪单个粒子的运动轨迹计算其速度。粒子追踪测速可通过2种方式实现：(a)分析顺序采集的、曝光时间较短的多帧图像数据，匹配同一物理粒子计算其位移(速度)；(b)计算较长曝光时间下的粒子光学轨迹长度[22]。近年来PTV技术除了在流体力学领域被应用于测量流场、泥沙沉速[23]、明渠流黏性底层[24]等以外，在岩土和结构方向也被逐渐应用于分析质点运动的位移、速度分布、压力分布等[25]。本研究使用高速摄像机对平衡状态下的砂土运动流场进行观测，获得时序列图像后使用PTV技术对每一帧桩身移动图像的相位进行定位，并使用PIV测量技术对各时刻进行砂土运动瞬时流场计算，再对不同周期相同相位的瞬时流速场进行平均，获相位平均流场。

1.6 试验分组情况

试验条件见表1。根据电机能力和偏心轮尺寸，试验设置的加载频率为1～5 Hz，加载位移幅值在0.42～2.33 mm，加载时间统一控制为72 h，保证加载频次在106以上。

表1 试验条件Table 1 Experimental conditions

2 结 果 分 析

2.1 单桩周围土体形态随时间变化过程

图3以工况8(x=2.06 mm，f=3 Hz)为例展示了振动72 h内桩基周围土体变形过程。在振动开始后(t=1/6 h)，模型桩两侧土面迅速出现沉陷，在贴近桩体处出现明显的沉陷坑。通过土表面示踪蓝砂可以看出，表面砂土沿桩壁下落后在桩的振动作用下向两侧迁移，形成一个小型的半心形区域。这一阶段说明初始土颗粒间仍较为松散，在振动作用下桩基础周围一定范围内土颗粒重新排列，土颗粒间空隙减小，土体密实度增大。这与Cuéllar等[9]描述的振动桩基周围土体沉降密实过程类似。

图3 振动桩基周围土体形态随时间发展Fig.3 Temporal development of soil pattern around a vibrating monopile

随后，上层的红黄混合砂也逐渐向下迁移，t=9 h时，从桩基周围的混合砂区域可以发现，土表面落下的蓝砂已经和红黄砂充分混合，混合砂区域在深度方向上发展更为强烈，在宽度方向上发展较为缓慢；对比t=1/6 h时可以发现，该阶段沉陷坑的深度几乎停止发展，仅在宽度上略有增长。

从t=24 h至t=72 h，沉陷坑深度和宽度已经几乎停止发展，沉陷坑边坡与初始土平面交界处出现明显的折角，说明桩周土体密实度已趋于恒定；桩基础周围混合砂区域宽度逐渐增加，而深度几乎停止增长；在混合砂区域内可以明显观测到黑砂颗粒，说明桩基础周围越来越多的土体参与了掺混运动。这一阶段与Cuéllar等[9]推测的砂土对流过程类似，土体密实度不再增加，砂土对流运动由桩土相互作用产生的摩擦剪切应力驱动并持续存在。

2.2 桩顶位移幅值和振动频率对桩周土体变形的影响

在试验各种工况下单桩周围土体变形的发展规律大致相同，但其平衡尺度、变化速率等受加载频率和加载位移幅值的影响会出现不同的结果。为了量化振动单桩周围土体变形、沉降和对流区域的形态变化，参考Li等[14]的定义方法，图4给出了具有代表性的4个几何尺寸，定义如下：(a)沉陷区深度(h)。该深度是指原土面与沉陷区坡底的竖向距离。(b)沉陷区宽度(b)。该宽度是指模型桩侧壁到沉陷区一侧坡顶的水平距离。(c)对流区深度(H)。该深度是指参与对流运动的土颗粒所能达到的最低点与沉陷区坡底的竖向距离。(d)对流区宽度(B)。该宽度是指参与发生对流运动的范围内土颗粒与模型桩侧边的最大水平距离。

图4 桩周砂土运动特征区域划分与定义Fig.4 Definition and division of characteristic areas of soil deformation around monopile foundations

在量化土体各特征尺度时，采用在图像上点取相应特征点的像素坐标计算出特征长度的像素数量，并根据单位长度的像素数量将其转化为长度的方法，误差约为±0.5 mm。为了验证试验的可重复性，对工况3进行了重复性试验分析(工况3-a)，发现2组工况中对流区轮廓接近，对流区宽度相对误差为5.2%，说明试验重复性良好。

2.2.1 桩顶位移幅值对土体变形的影响

图5给出了4组试验土体变形特征尺度随时间变化的关系，通过比较工况1～4分析位移幅值对其影响。

图5 不同位移幅值作用下各特征尺度随时间发展特性Fig.5 Temporal developments of characteristic scales under the effect of different displacement amplitudes

由图5(a)(b)可见，各工况条件下沉陷区尺度经过前期的快速发展后(t=5 h)，会进入极其缓慢增长甚至不增长的阶段，且在振动频率相同的情况下，桩顶位移幅值越大，在最终时刻(t=72 h)沉陷区尺度也越大。图6(a)(b)展示了桩顶位移幅值与t=72 h时沉陷区深度、宽度的关系，由图6结果可见，桩顶位移幅值与t=72 h时沉陷区尺度基本呈线性关系。从图5(b)还可以得出，工况1～4沉陷区宽度最后48 h增长率分别为2.4%、6.8%、7.1%和8.2%，这说明振动频率一定时，桩顶位移幅值越大，沉陷区尺度越难以到达平衡。这是由于桩顶位移幅值越小，桩土相互作用的强度也越小，而振动时桩周土体的密实度增加会限制桩土接触面处的桩身位移，对小幅振动位移影响更为明显，沉陷区尺度越容易达到平衡。

图6 各特征尺度在最终时刻与桩顶位移幅值的关系Fig.6 Relationship between displacement amplitudes of pile-top and final values of each characteristic scale

由图5(c)(d)可见，在振动频率相同的情况下，桩顶位移幅值越大，对流区尺度的初期增长速率和最终时刻(t=72 h)结果也越大。结合Cuéllar等[13]对桩周砂土对流区的分析可知，砂土对流运动由桩土相互作用产生的摩擦剪切应力驱动并持续存在，本研究中桩顶振动幅值越大，桩壁和土体接触面的位移变形也就越大，作用深度也会更深，直接导致对流驱动摩擦剪切应力的增加，从而增大了对流区的尺度和对流速度。关于对流速度的结果对比会在2.5节中进行讨论。由图6(c)(d)可见，桩顶位移幅值与对流区宽度、深度同样呈线性相关。图5(d)中，工况1～4对流区宽度最后48 h增长率分别为2.8%、26.3%、28.3%和36.3%，同样可见振动频率一定时，桩顶位移幅值越大，对流区尺度越难以到达平衡，且对流区达到平衡所需时间比沉降区更久。

2.2.2 振动频率对土体变形的影响

图7给出了5组试验土体变形特征尺度随时间变化的关系，通过控制相同桩顶位移幅值(2.06 mm)对比不同加载频率下土体各特征尺度随时间的变化。

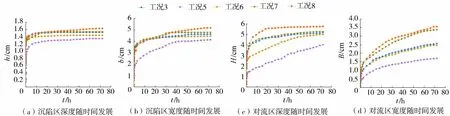
图7 不同加载频率下各特征尺度随时间发展特性Fig.7 Temporal development of characteristic scales under the effect of different loading frequencies

与图5类似，图7中各工况沉陷区和对流区特征尺度随时间发展都遵循先快速发展后趋于平衡的两段式发展规律。加载频率越大，各特征尺度前期增长速率和最终时刻的结果也越大。相比较振动幅值的影响，由加载频率增加引起的沉降和对流尺度增长速率偏小。由图8可以看出，桩顶位移幅值一定时，加载频率与沉陷区和对流区尺度的最终值也基本呈线性相关。这一点与赵家林[15]的试验结果不同，其研究发现沉陷区平衡深度随加载频率变化是非线性的，随着加载频率的增加，平衡尺度增长速率会变大。这一区别的主要原因是赵家林的试验工况在改变振动频率时没有对桩顶振动位移幅值进行控制，振动频率越大则越接近模型桩固有频率，导致模型桩位移增大。而图7中的5组试验中固定了桩顶位移，改变振动频率时没有出现桩顶位移变化，所以最终沉陷区尺度与加载频率呈线性关系。

图8 各特征尺度在最终时刻尺度与加载频率的关系Fig.8 Relationship between loading frequency and final values of each characteristic scale

对比图5和图7还可以看出，准平衡时刻沉降坑深度与对流区深度比值范围为h/H=0.24～0.34，沉降坑宽度与对流区宽度比值范围b/B=1.47～2.34。这说明桩基振动在深度上对砂土对流影响更大，宽度上对砂土沉降影响更大。

2.3 不同深度的桩身水平位移幅值随时间变化

关于桩基振动引发砂土对流运动产生的原因，Cuéllar等[9]和赵家林[15]认为当桩体振动时，桩基础周围土体会由于重力和砂土之间摩擦剪切应力驱动作用沿着桩土界面周期性开合的“缝隙”掉落而向下运动，且这种桩土之间的开合“缝隙”尺度大于砂土颗粒的粒径时对流才会比较明显。为了验证这一推论，本试验选取工况9(f=5 Hz ,x=2.33 mm)，对其72 h桩土相互作用全过程进行观测，采用PTV技术，量化土面下不同埋深处桩身的水平位移演变过程。

图9展示了桩基振动过程中，不同埋深处桩身水平位移幅值的演变特性。从结果可以看出，随着桩周砂土沉降和对流运动的进行，桩身各点位移逐渐减小，最后趋于平衡；桩身距离初始土表面越远，达到平衡所需要的时间越短。桩身水平位移幅值在振动前期(t=0～5 h)迅速减小，前20 h之内几乎达到平衡，对照图5、图7，可以发现该发展趋势与沉陷区深度与沉陷坑宽度发展变化趋势相似。其原因为土体在振动初期较为松散，振动开始后，桩周附近土体局部密实度迅速增大，导致模型桩基础的整体刚度变大，桩身位移幅值减小；在振动后期，桩周砂土密实度趋于平衡，土体基础刚度趋于不变，桩身位移幅值也近似趋于平衡。

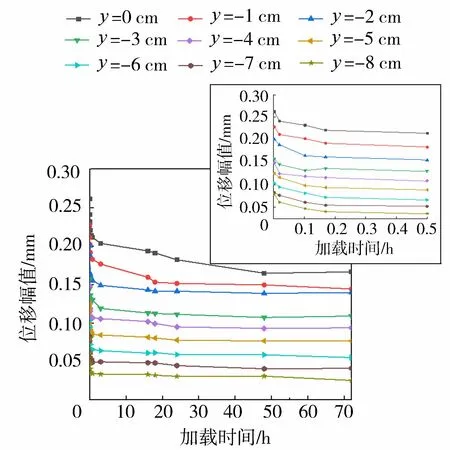
图9 工况9不同深度桩身水平位移幅值随时间变化Fig.9 Temporal development of lateral displacement amplitudes of the monopile at different embedded depth for Test 9

由图9可以发现，初始土面处(y=0 cm)的桩身初始和最终时刻位移幅值分别为0.26 mm和0.17 mm，均小于本试验用砂的中值粒径0.48 mm，因此可以推断在桩基振动过程中桩土界面的“缝隙”不足以使砂土颗粒掉入，可见前人对土颗粒产生对流运动的原因理解并不准确，对流运动的产生不需要桩土界面桩身变位大于砂粒粒径。通过图9的试验结果可以推测，在砂土对流阶段桩周砂土沿桩身向下所承受的挤压力呈减小趋势，这种挤压力的减小使土层之间的摩擦剪应力产生梯度差，持续驱动砂土颗粒的对流运动。

2.4 准平衡状态下桩周沙土颗粒瞬时流场特性

图10展示了工况7在t=72 h时，6个不同振动相位状态下桩周砂土运动的瞬时流场(相位平均)，其中t为振动时间，T0为振动周期。由于桩顶振动规律近似正弦运动，当t/T0=0/8和t/T0=4/8时，桩体处于位移幅值处，此时颗粒运动瞬时速度为0，流场图为空白，本文不做展示。图11展示了工况7在t=72 h时，桩体在y=0 cm处的水平位移和水平瞬时速度随时间演变过程。由图11可以发现，本试验加载装置输出稳定，桩体水平振动位移基本符合正弦规律，桩体瞬时速度演变趋势与位移对应良好。

图10 工况7不同振动相位状态下砂土运动的瞬时(相位平均)流场Fig.10 Instantaneous (phase-averaged) velocity fields of soil movements at different vibrating phases in Test 7

图11 工况7桩体振动位移与瞬时速度Fig.11 Vibration displacement and instantaneous velocity of pile in Test 7

由图10可以发现，砂土对流平衡状态下，桩周土颗粒运动的瞬时速度在10-1cm/s量级，与图11中桩体振动速率的速度量级一致。对流区颗粒运动瞬时速度方向与桩体运动方向一致，在t/T0=0/8至t/T0=4/8时土颗粒随桩向右运动，在t/T0=4/8至t/T0=8/8时土颗粒随桩向左运动。颗粒瞬时流速大小随桩身振动相位变化而变化，在桩身位移最大处速度最小，在桩身处于中立位置处速度最大。各相位时刻，桩周砂土运动流速量值趋势具有类似的特性：水平方向上，桩侧越靠近桩的位置流速越大，且速度大小逐渐向两侧递减；竖直方向上，自沉陷坑坡底往下0.8～1.5h范围内流速最大，超出这个范围后流速向下减小。图11中虚线代表平衡状态下对流区范围，可以发现可见砂土颗粒的实际运动范围大于砂土对流区范围。

2.5 准平衡状态下沙土颗粒对流运动时均流场

图12展示了各工况在砂土颗粒对流运动准平衡状态(t=72 h)下的时均流场，因为时均流场基本左右对称，图中仅展示左半边的流场。由结果可以看出，各工况在准平衡时刻的流场形态基本相似：桩基附近出现近似心形的对流区，上层土面的土颗粒沿沉陷坡向桩迁移，随后沿桩壁向下迁移，然后向远离桩的方向迁移，最后重新向上迁移回到土表面，形成对流区。图12(a)(b)(c)展示了相同振动频率(3 Hz)，不同桩顶位移幅值(1.42 mm、2.06 mm、2.33 mm)的3组试验振动72 h时的平均流场。从结果可以看出，随着桩顶振动幅值的增大，砂土颗粒对流范围增大，流速也明显增大；图12(d)(e)(f)展示了桩顶位移幅值相同(2.06 mm)、不同振动频率(2 Hz、4 Hz、5 Hz)的3组试验振动72 h时的平均流场，从结果可以看出随着振动频率的增大，砂土颗粒对流范围和流速同样明显增大，最大流速出现在桩壁附近。从宏观上来看，砂土在长期循环荷载作用下的对流运动十分缓慢，平衡状态下的平均流场速度量级为10-4cm/s。对比图10可以注意到，桩基周围土颗粒运动瞬时速度量级和平衡状态下桩基础周围土颗粒运动的平均速度量级相差千倍，由此可以更好地理解桩基及其周围砂土在长期循环荷载作用下的运动响应过程：桩基础振动时，桩基附近一定范围内(大于对流区)的土颗粒会随着桩基的振动做往复运动，这种往复运动速度相对较快，桩基每振动一个循环内“往”和“复”过程的砂土颗粒流速会发生不完全抵消，产生一个相对较小的差值，构成微小的位移；在大量循环作用之后，这些微小位移不断累加，逐渐形成了颗粒的对流趋势。

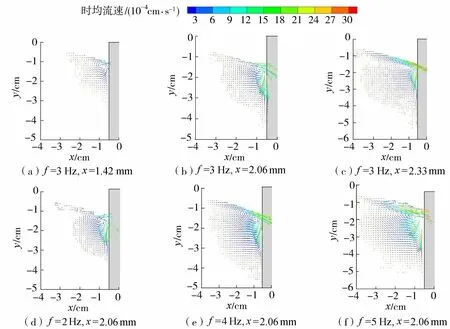
图12 各工况平衡状态下砂土颗粒对流运动时均流场Fig.12 Time-averaged velocity fields of soil particle convective motions at equilibrium state for different tests

3 结 论

a. 土体特征尺度随时间均经历前期快速增长阶段和后期趋于平衡两个阶段；桩顶加载频率和位移幅值与土体变形各特征尺度均基本呈线性关系，加载频率和桩顶位移幅值越大，土体变形特征尺度也越大。

b. 单桩在长期水平循环荷载作用下，桩身各点水平位移幅值在振动开始后的几小时内迅速减小而后平衡，桩身距离初始土表面越远(埋深越深)，其水平位移幅值达到平衡所需要的时间越短；当初始土面处的桩身位移幅值远小于桩周砂土颗粒的中值粒径时，桩周砂土对流运动仍然可以由桩土相互作用产生的摩擦剪切应力驱动并持续存在。

c. 准平衡状态下，桩周砂土运动瞬时流态与桩体振动相位密切相关，桩壁附近瞬时流速量级与桩体运动速度量级相同；砂土对流运动可以看成是长期水平循环荷载作用下瞬时流场的叠加效应，其速度比桩体运动速度低3个量级。