基于遗传算法的SVM-AR改进模型与应用

王红瑞，魏豪杉，胡立堂，赵自阳，娄和震

(1.北京师范大学水科学研究院，北京 100875； 2.中国科学院地理科学与资源研究所，北京 100101；3.中国科学院大学资源与环境学院，北京 100190)

水文过程的复杂性和随机性，导致其存在强烈的非线性，传统的回归、时间序列等方法难以很好地预测其变化，而支持向量机、神经网络等机器学习方法可以更好地解决这类问题[1-5]。与神经网络等机器学习算法相比，支持向量机及其相关方法在水文预报方面具有独特的优势[6-11]。

近年来，支持向量机(support vector machine, SVM)被广泛应用于水文时间序列的分析中且被不断地改进。部分学者将支持向量机与智能优化算法结合，通过改进智能算法的过程提升支持向量机参数的率定精度，从而提升支持向量机的预测精度，如李天宏等[1]改进粒子群算法，结合支持向量机算法提升径流预报效果，张岩等[12]利用构建的PCA-PSO-SVR算法对丹江口水库年径流进行预报。部分学者通过使用其他模型或分析方法与支持向量机耦合得到混合模型，提升预测精度，如，王红瑞等[8]基于小波变换构建的支持向量机模型的预测精度比传统的支持向量机和神经网络模型更高；Bafitlhile等[10]通过进化策略(ES)优化方法对支持向量机与神经网络的参数进行优化和比较，发现支持向量机在流域水流模拟中要优于神经网络方法；Baydarolu等[13]构造了基于小波分析、奇异谱分析和混沌方法的支持向量机耦合模型预测河流流量；Meng等[11]改进EMD-SVM得到的M-EMDSVM比传统SVM方法能更准确地预测强非平稳径流；梁浩等[4]、周婷等[14]基于小波分析，提升支持向量机预测精度；贺玉琪等[15]耦合支持向量机和贝叶斯岭回归的BRR-SVR优化模型，并将其应用于月降水量预测；朱双等[16]利用基于灰色关联分析的模糊支持向量机方法进行径流预报。还有一部分学者通过改进支持向量机的核函数，构造混合核函数，以提升支持向量机对径流预报的预测精度，如唐奇等[17]将多项式核与径向基核线性组合构造混合核函数提升预测精度；刘昕玥等[18]利用改进的自适应遗传算法确定二核的混合核函数参数，进行流域的流量预报。但在确定混合核函数各个核函数的比重参数时，文献[17-18]并未给出较合理的混合核函数比重参数的确定方法。在实际问题中，各个核函数的比重参数是无法预先确定的，即使预先给定这些参数也无法保证所构造的混合核函数的预测效果会优于单一核函数，也就是说，文献[17-18]主要说明了混合核函数的可用性，但没有给出混合核函数的用法，而本文给出了一种混合核函数的具体使用方式。

针对文献[17-18]存在的问题，本文随机产生足够多的混合核函数比重参数样本，通过这些参数得到若干个流量预报结果，取中值确定最终的预报结果。本文采用的支持向量机算法的核函数包括三核混合核函数、二核混合核函数与单一核函数，采用遗传算法确定核函数参数。但无论采用何种智能算法，得到的核函数参数值都存在不确定性，针对这一问题，本文基于已有数据构造函数对核函数参数以及核函数类型进行选择，以减少这种不确定性。

1 基于SVM的时间序列模型构建

1.1 时间序列分解

(1)

{St}为有周期性的序列，需要进行处理的是{Tt}以及{It}。对{Tt}和{It}进行平稳性分析，若序列为非平稳序列，则通过差分等方式把序列平稳化。

1.2 SVM-AR模型构建及平稳性分析

自回归滑动平均模型ARMA(p,q)为

Xt=φ0+φ1Xt-1+…+φpXt-p+εt-θ1εt-1-θ2εt-2-…-θqεt-q(φp≠0,θq≠0)

(2)

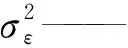
利用ARMA(p,q)模型建立基于支持向量机的时间序列模型：

Xt=fsvm_ar(Xt-1,Xt-2,…,Xt-p)+Iqt

(3)

其中Iqt=εt-θ1εt-1-θ2εt-2-…-θqεt-q

式中：fsvm_ar(·)——支持向量机预测函数。

自回归模型AR(p)为ARMA(p,q)中q不存在的特殊情况：

Xt=φ0+φ1Xt-1+…+φpXt-p+εt

(4)

1.3 模型定阶

为确定ARMA(p,q)模型的阶数p、q，本文采取以样本自相关系数与偏自相关系数判别为主，AIC(Akaika’s information theoretic criterion)、BIC(Bayesian information criterion)或称SBC(Schwartz’s Bayesian criterion)定阶为辅的模型定阶方法。

样本自相关系数为

(5)

样本偏自相关系数为

(6)

当样本容量n充分大时，样本的自相关系数和偏自相关系数均近似服从正态分布，即

(7)

由正态分布性质可得

(8)

式中：Pr(·)——正态分布的分布函数。

截尾阶数，即该阶数后自相关系数或偏自相关系数趋于零，否则为拖尾。

故可以利用2倍标准差的范围进行判断，从而模型定阶结果见表1。由表1可知，上述定阶方法仍具有一定的不确定性，若出现数种均满足模型定阶条件，或模型阶数较为模糊的情况，可以采用AIC或者SBC(BIC)定阶准则进行最终的模型定阶。AIC准则由日本统计学家Akaike[19]于1973年提出，SBC(BIC)准则是为弥补AIC准则在样本容量趋于无穷大时，所选择模型不收敛于真实模型而提出的基于Bayes理论的判别标准。AIC准则考虑的是所建模型拟合精度与未知参数个数的综合最优配置，是拟合精度与参数个数的加权函数：

表1 模型定阶结果Table 1 Model ordering results

SAIC=-2lnMvalue+2Nparameter

(9)

SBC准则对AIC稍加改动，定义如下：

SSBC=-2lnMvalue+lnNparameter

(10)

式中：Mvalue——模型的极大似然函数值；Nparameter——模型中未知参数个数；SAIC——AIC准则计算结果；SSBC——SBC准则计算结果。

在合理范围内，2个准则的取值均是越小越好，但AIC与SBC在模型定阶时可能会出现不一致的情况，本文优先选择SBC准则。

2 支持向量机核函数构造与参数确定

支持向量机是统计学习中常见的应用于数据分类、预测的方法，核函数是支持向量机的核心，由Aizerman、Braveramann与Rozoener于1964年提出并在机器学习领域引入的理念[20]。核函数方法首先通过特征空间映射，把原输入空间的数据映射到合适的特征空间, 然后在该特征空间中分析、提取数据特征，进行相关运算。该方法的优势在于，以内积的形式实现非线性变换，避免了维数过大而造成的“维数灾难”。支持向量机通过引入核函数，直接计算高维特征空间中的内积，实现将输入空间升维的非线性变换，降低了计算的复杂性。核函数有多种类型，核函数类型的选择会直接影响支持向量机预测结果的好坏。

支持向量机的主要思想如下：给定训练样本D={(x1,y1),(x2,y2),…,(xm,ym)}，其中，xi∈n是输入向量，yi∈是输出指标(i=1,2,…,m)。希望寻求一个n上的实值函数f(x)，使得对任意x，f(x)与y能尽可能接近。首先将原始空间中的数据映射到一个高维空间中，然后在高维空间中进行线性拟合，设映射后的回归函数为f(x)=ωTφ(x)+b，其中φ(·)为n到高维特征空间中的非线性映射，ω为超平面的权值向量，b为偏置。从而由最优化理论可以把该回归问题转化为

(11)

式中：CN——正则化常数；lε——ε-不敏感损失函数。

(12)

(13)

引入拉格朗日乘子，可以得到上最优化问题的对偶问题：

(14)

(15)

式(14)中K(xi,xj)=φ(xi)Tφ(xj)为核函数。可以发现K(·,·)为对称函数，若K(·,·)是定义在空间上的对称函数，那么K是核函数当且仅当对于任意数据{x1,x2,…xm},xi∈n，核矩阵Κ总是半正定的[21]:

(16)

所以核函数的线性组合或直积也是核函数，表2给出了本文采用的3种常见核函数：径向基核函数、多项式核函数、Sigmoid核函数的表达式，参数名称和参数范围等，以及通过线性组合构造的混合核函数的表达式和混合核比重参数的名称符号。并通过传统的遗传算法，确定表2单一核函数相关参数。

表2 核函数表达式、参数及范围Table 2 Expression, parameters and range of kernel function

流域月径流量预测的流程如图1所示，首先对流域的月径流量进行分解，随后对分解得到的流域长期趋势序列、随机波动序列进行平稳性检验与处理、模型定阶，再通过SVM算法进行预测，最后将数据整合，得到最终的预测结果。

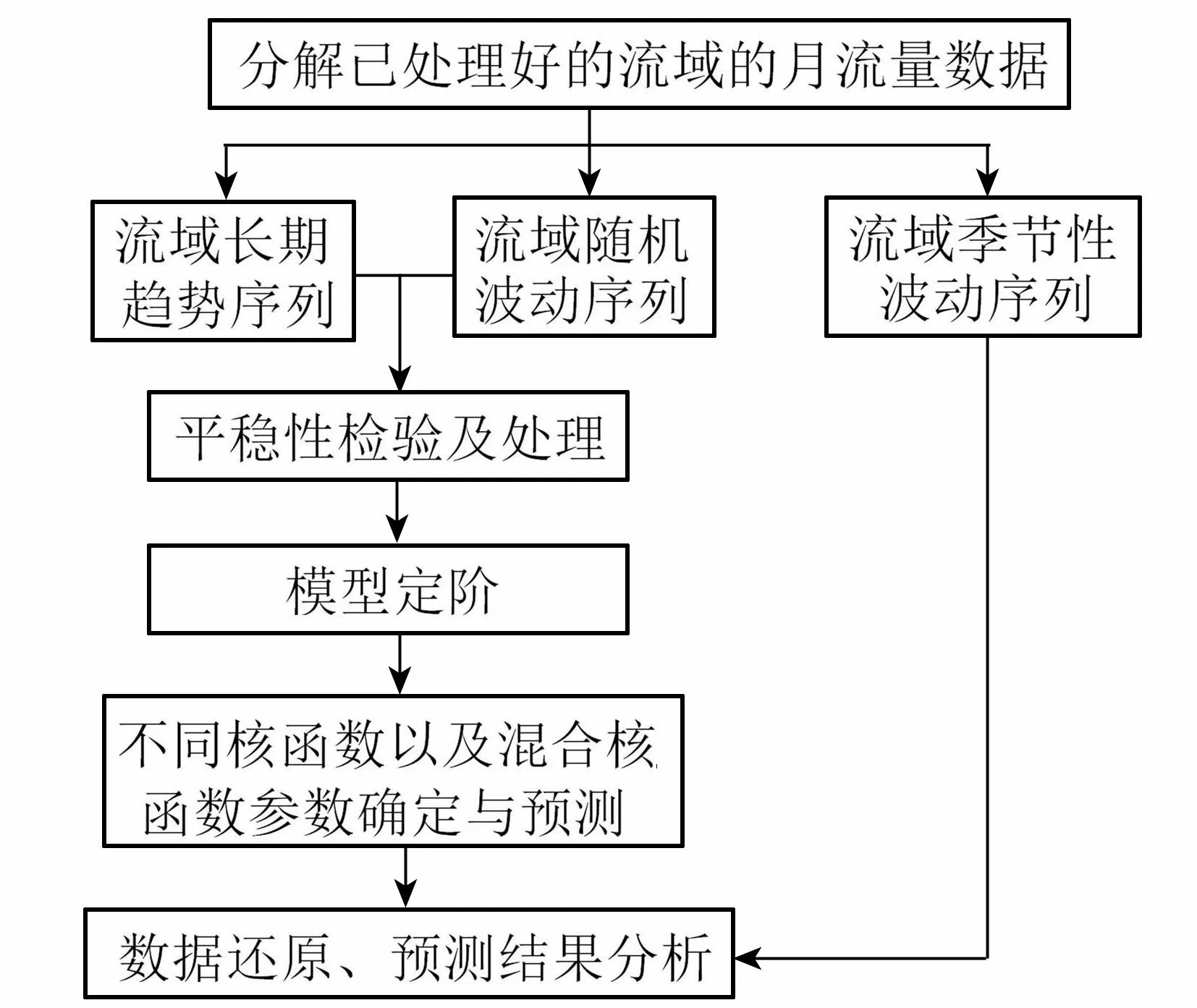
图1 SVM-AR流程Fig.1 SVM-AR flowchart

3 实 例 分 析

3.1 月流量数据时间序列分析

3.1.1 流量数据分解以及平稳性分析

将渭河流域咸阳站1960年1月到2001年12月的逐月流量按近似4∶1(实际为50∶13)划分为训练集与检验集。首先，对逐月流量的训练集进行确定性分析，通过乘法模型对该序列进行分解，得到长期趋势序列、季节波动序列、随机波动序列(图2)，随后分别对长期趋势序列以及随机波动序列进行平稳性分析。经平稳性检验，训练集中的月流量长期趋势序列不是平稳序列，故对其进行1阶差分，差分后的序列经检验为平稳的时间序列，随机波动序列已经为平稳序列，不再进行其他操作，检验结果可见表3。

图2 渭河流域咸阳站月流量数据分解Fig.2 Monthly data decomposition for Xianyang Station of Weihe River Basin

表3 咸阳站月流量时间序列平稳性检验结果Table 3 Stationarity test result of monthly runoff time series for Xianyang Station

3.1.2 模型定阶

分别绘制渭河流域差分后的月长期趋势波动(简称月趋势)序列和随机波动序列的自相关图与偏自相关图，如图3所示，图中蓝色阴影为自相关图或偏自相关图的95%置信区间。由图3可以初步确定经过1阶差分后流域长期趋势序列的阶数大致为的p=4、5、6，q=4、5、6，随机波动序列的阶数大致为p=1、2、3，q=2、3、4。由图4确定具体的阶数：1阶差分后的流域长期趋势序列阶数为p=5，随机波动序列阶数为p=2。

图3 渭河流域咸阳站各时间序列的自相关和偏自相关图Fig.3 Autocorrelation graph and partial correlation graph of each time series for Xianyang Station of Weihe River Basin

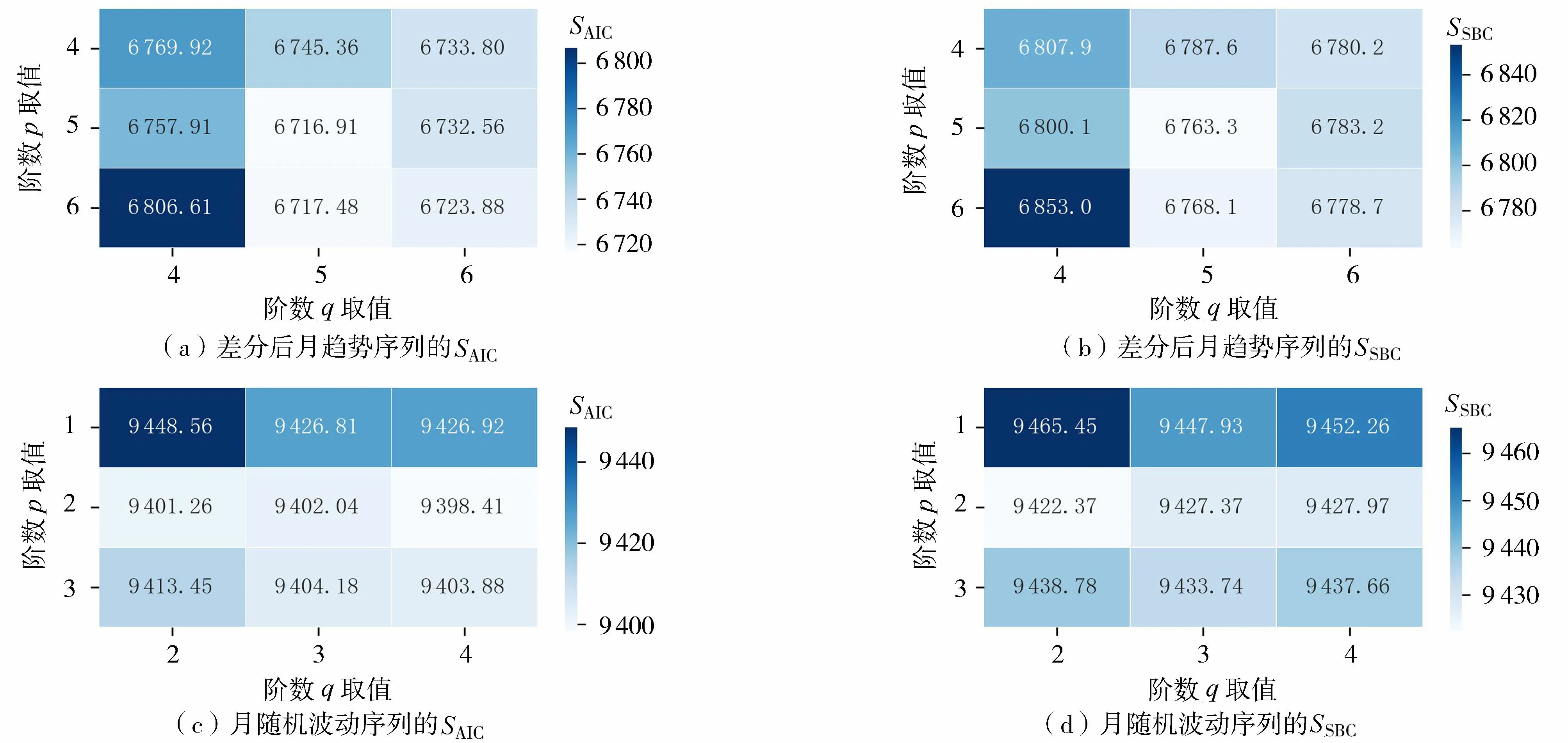
图4 各时间序列的SAIC、SSBC热度Fig.4 SAIC and SSBC heat maps of each time series

3.2 支持向量机算法使用流程

采用遗传算法在测试集上进行参数确定，使目标函数最小化，目标函数为：测试集“5折交叉验证”的均方误差最大值。每一个单一核函数的参数都用遗传算法率定一次参数，由于遗传算法具有随机性，所以每一次遗传算法率定的参数都有差异。随后构造混合核函数，由于作用在检验集之前，无法预知单一核函数或者混合核函数的预测效果，所以本文构造的混合核函数是建立在已知单一核函数的基础上的，混合核函数的核函数参数是前面已经确定的单一核函数的核函数参数，惩罚参数取参与构成混合核函数的单一核函数惩罚参数的最小值。本文不通过遗传算法对混合核函数所有参数进行重新率定，原因是参数太多，带来的不确定大大增加，且运算量很大，经检验，预测效果反而不如单一核函数。

通过遗传算法确定支持向量机核函数参数后，还需要确定混合核函数的混合核比重参数，即各个核函数的比例。由于实际问题中观测流量值无法事前得到，所以各个核函数所占的比重事先无法确定，故依据统计学相关理论，随机产生数量足够大的样本进行预测。对于三核混合核函数，随机产生500组混合核比重参数，得到500条预测流量曲线，取它们的中值作为最终的预测流量曲线。对二核混合核函数，随机产生450组由2个单一核函数构成的混合核函数比重参数(每种组合50组，9种组合共450组，9种组合分别是：长期趋势数据集的3种二核混合函数与随机波动数据集的3种二核混合函数的交叉组合)，得到450条预测流量曲线，取它们的中值作为二核混合核函数最终的预测流量曲线。单一核函数取9组预测流量曲线的中值作为最终的预测流量曲线。

由于遗传算法具有一定的随机性，在没有观测流量的情况下，无法预知核函数参数的合理取值。现有数据只有遗传算法确定核函数参数后产生的若干条流量曲线(即3类核函数产生的500+450+9条流量曲线)，所以分别通过三核混合核函数500条流量曲线两两之间的均方误差集合(记为EMSE3)，二核混合核函数450条流量曲线两两之间的均方误差集合(记为EMSE2)与单一核函数9条流量曲线两两之间的均方误差集合(记为EMSE1)之间的关系对核函数参数进行选择。运行遗传算法30次，得到集合EMSE1、EMSE2、EMSE3的方差，见表4。

表4 检验集30次遗传算法的运行结果Table 4 Running results of 30 genetic algorithms on the test set

由表4可知，多数情况下VMSEpo2比VMSEpo1和VMSEpo3大，或者介于两者之间；VMSEpo3数次达到130以下，这是其他2种情况达不到的；VMSEpo1保持在130～180之间，未出现超过200的情况，比其他2种更稳定，所以优先考虑均方误差能达到最小值的三核混合核函数和稳定性最好的单一核函数。构造如下形式的函数MF、MM：

(17)

MM=VMSEpo3-VMSEpo1

(18)

运行遗传算法30次后得到的MF与MM间有强线性关系，相关系数为0.63，拟合曲线为

(19)

拟合曲线参数经T检验得到的p-值为6.06×10-5≪0.05，说明拟合效果良好。这说明MF越小，MM越小，故而在先验条件下，期望MF数值尽量小，MF足够小时，MM会小于零，即VMSEpo3

核函数参数选取与流量预测流程：(a)遗传算法确定若干组核函数参数；(b)确定每组的三核混合核函数、二核混合核函数和单一核函数的均方误差集合，并据此计算MF，找到MF最小的一组，记为组1；(c)通过组1参数产生若干条三核混合核函数(此处是500条)的预测流量曲线，取中值得到最终的预测流量曲线。

3.3 结果与分析

通过遗传算法另产生10组参数进行验证，得到10组MF,按照MF从小到大排列得到图5，每张子图箱线图上方为每类核函数的最终预测流量曲线与实际观测流量曲线之间的均方误差。可以看到MF最低时，虽然三核混合核函数得到的最终预测流量曲线与实际观测流量曲线的均方误差不是10次中的最小值，但也是达到了132这一较低值，图5中MF较低的组1～3三核混合核函数的预测结果均保持较低值：132、138、129。尽管图5(a)中结果不是最好的(最好的结果为图5(g))，但这在无实际观测流量的前提下，可以保证最终的预测结果精度处在较高水平(即均方误差处在较低水平)，大大降低了核函数参数确定过程中的不确定性。依照3.2中的流程，采用图5(a)中的支持向量机核函数参数(即使MF最小的核函数参数)进行后续工作。

图5 检验过程中集合EMSE1、EMSE2、EMSE3的箱线图Fig.5 Box plot of EMSE1、EMSE2、EMSE3 in inspection process

首先考察该参数下，3类核函数的最终预测流量曲线差异。三类核函数的最终预测流量曲线如图6所示。除均方误差外，再引入2个额外指标：相关系数与相对误差的绝对值(简称相对误差)，相对误差取绝对值是为方便比较。

图6 检验集上不同核函数预测结果趋势Fig.6 Trend chart of prediction results of different kernel functions on the test set

由图6可知，三核和二核混合核函数在此时基本处于同一水平，均高于单一核函数预测精度。在流量较低的年份，单一核函数的预测值较高，混合核函数相比单一核函数的预测结果更接近实测流量值；流量较高的年份，混合核函数能一定程度上降低流量峰值错峰带来的误差。三核混合核函数预测结果的均方误差能够将单一核函数预测结果的均方误差从150左右降低到130左右，使精度得以提升。根据3.2中流程，图6(a)中预测流量变化曲线为最终的预测结果。

由图7可知，在随机的混合核比重参数下，三核混合核和二核混合核的均方误差与相对误差都可能取到远比单一核函数差或者远比单一核函数好的情况，这说明混合核函数的混合核比重参数值无法事先确定，因为给定的混合核比重参数，可能会使预测效果变好，同样也可能会使预测效果变差，但此时混合核得到的均值和中值都好于单一核函数，与最终的预测结果基本相当。3类核函数的均值和方差的相关系数基本处于同一水平，都达到0.5以上，说明3类核函数的预测流量与实际观测流量均具有较强的相关性，预测效果均良好。

图7 不同类型核函数预测效果的均方误差、相对误差、相关系数箱形图Fig.7 Mean square error, relative error and correlation coefficient box plots of different types of kernel function prediction effects

4 结 语

本文给出确定核函数参数的方法：通过遗传算法(或其他优化算法)，给定若干组核函数参数，通过计算函数MF，取MF最小值时的核函数参数进行后续的预测工作。同样，为确定实际问题中混合核函数的混合核比重参数，通过随机产生足够多的混合核比重参数，得到足够多的预测流量曲线，并取这些预测流量曲线的中值作为最终的流量预测值。

多数情况下二核混合核函数的预测结果都介于三核混合核函数与单一核函数之间，尽管二核混合核函数也可能出现略好于三核混合核函数和单一核函数的情况，但这种“略好”并不明显，总是与三核混合核函数或者单一核函数较好的一方相当，所以本文主要考虑了三核混合核函数与单一核函数之间的关系，得到了核函数参数选取方法，最终的预测结果也推荐采用三核混合核函数的预测结果。

采用本文构造的方法，能够得到较好的预测结果。尽管这种预测结果可能不是最优的，但是它在流域未来流量未知的情况下，能够保证预测的精度处在所有可能预测结果中的较高水平，大大降低了核函数参数选取时带来的不确定性。

采用和构造的混合核函数是在单一核函数上产生的，能够一定程度上提升单一核函数的预测精度，但如果单一核函数出现“错峰”问题(即洪峰错位的情况)，混合核函数也会出现，如何能够解决“错峰”问题，是日后亟须解决的问题。另外，本文采用的是线性组合的方式构造混合和函数，还有其他的混合函数构造方法，如直积等，也有很大的研究与发展空间。