三种机器学习模型在太湖藻华面积预测中的应用

吴 娟，朱跃龙，金 松，杨 涛，冯 钧，吴志勇，薛 涛，姜悦美

(1.太湖流域管理局水文局(信息中心)，上海 200434； 2.河海大学水文水资源学院，江苏 南京 210098)

太湖(119° 52′ 32″E～120° 36′ 10″ E、30° 55′ 40″N～31°32′58″N)是我国第三大淡水湖，水面面积约2 338 km2，是典型的大型浅水湖泊。近几十年来，太湖蓝藻水华(以下简称“藻华”)呈现非线性、复杂性等特点[1]。藻华不完全是本地蓝藻短时快速生长暴发所致[2]，而是已经成为优势种群的蓝藻在合适条件下，受物理(温度[3]、光照[4]、水动力[5]等)、化学(氮、磷[6]等)[7]、生物(与其他藻类的竞争)[8]因素等共同影响，在较短的时间里改变水平与垂直位置形成“暴发”[9]，因此，藻华本质是藻类生物量在水体中逐渐增加、上浮、聚集、迁移的过程[10]。藻华扩张分为时间扩张、空间扩张和生物量扩张。时间扩张用藻华持续时间、发生时间等表征，空间扩张用基于遥感影像的藻华面积表征，生物量扩张用叶绿素a、浮游植物总生物量等表征[11]。由于生物量统计主要以特定湖区采样监测、计数鉴定方法为主，受制于采样站点的位置与频次，获取资料困难，因此，本文以研究藻华时间、空间扩张为主。

研究表明，气候变化、水体富营养化是太湖藻华增多的重要原因[12]。大面积偶发性太湖藻华受气象因子影响较大，而大面积频发性藻华主要受营养盐空间分布影响[13]。太湖处于较高的营养盐水平，超过藻华发生的阈值[14]，但季节性营养盐抑制过程[15]对藻华强度有一定的限制作用[16]，足以维持水华持续发生[17]。杭鑫等[18]认为气温、风、降水等气象因子对太湖藻华影响较大，适宜的气象因子为藻华暴发提供了有利条件。秦伯强等[19]研究表明：藻华面积形成过程较复杂，蓝藻细胞生长阶段，营养盐浓度、温度、光照等因素为藻华提供了物质基础；在蓝藻水华暴发阶段，藻华面积空间分布则受蓝藻细胞团浮力作用与水动力湍流作用的共同影响，风速决定藻华垂向分布，风向和风速共同决定其水平分布。

蓝藻生态动力学模型因过程复杂、参数众多[20]，导致应用在预测中存在一定的困难，而机器学习算法(如神经网络等)为太湖藻华预测提供了新的理论和方法[21]。机器学习是一门研究计算机模拟或实现人类活动的学科[22]，也是知识发现、数据挖掘的重要基础[23]。通过挖掘数据背后的深度价值和内在联系[24]，机器学习具有高度的非线性与灵活性[25]，应用于短期降水预报[26]、径流预测[27]、藻华预警[28]，有效提升了预报精度和效率。张艳会等[29]采用BP人工神经网络和模糊理论，建立了藻华发生的模糊风险评价方法；于家斌等[30]提出基于长短期记忆(LSTM)循环神经网络(RNN)藻华预测模型(LSTM模型预测精度较高,对样本具有较好的适应性)；罗晓春等[31]采用随机森林机器学习算法分析同期气象因子与藻华综合指数的关系，定量评估影响藻华的主要气象因子的贡献率。上述研究为太湖藻华的预测预警与风险管理提供了参考。

太湖湖面宽广，一般采用野外观测和数值模拟研究湖流导致藻华迁移和堆积。风向分布具有不均匀性，并随着风速减小差异有所扩大。在低风速条件下，无法形成稳定环流，蓝藻容易在太湖表面积聚，而此时各湖区之间风向差异较大，需要借助蓝藻生态动力学模型深入研究。本研究侧重采用全太湖、分湖区建模的思路，基于支持向量机(SVM)、长短记忆神经网络(LSTM)、极端梯度提升树(XGBoost)模型，快速预判各湖区藻华面积，旨在为太湖藻华预测预警、风险管理提供技术支撑。

1 数据与方法

1.1 数据来源

按照岸线、水质和水下地形等因素，太湖可分为竺山湖、梅梁湖、贡湖等[32]，见图1。近年来，中分辨率成像光谱仪(MODIS)数据因其光谱分辨率高、观测周期短等特点，广泛应用于太湖藻华动态监测[33]。考虑到太湖藻华每年4月开始零星暴发，12月以后基本无大范围藻华暴发，因此，选取4—11月的 EOS /MODIS 影像数据(排除了云层、天气质量等对影像质量影响较大的数据)共761景，时间间隔从1 d到15 d不等，藻华面积来源于中国科学院南京地理与湖泊研究所解译成果。本研究采用的藻华面积为绝对面积，指当像元内存在水华时，只计算像元内水华覆盖部分的面积。太湖内共布设33个监测点，覆盖了全部水域，监测项目包括pH、总磷、总氮、高锰酸盐指数、氨氮、叶绿素a、蓝藻密度，仅每月上旬监测1次，根本无法满足藻华面积建模要求，因此本研究只能采用环湖10个水质站、4个气象站时间分布较精细的数据进行建模。水质指标包括水温、pH、电导率、溶解氧、氨氮、总磷、总氮、浊度、高锰酸盐指数，气象指标包括气温、风速、风向、降水。本研究的资料序列均为2014—2018年。由于东部沿岸区与东太湖没有MODIS藻华资料，而贡湖、南部沿岸区均有水源地，因此，本研究采用全太湖、贡湖、南部沿岸区、中西北湖区(西部沿岸区+湖心区+竺山湖+梅梁湖)分别建模。南部沿岸区代表站包括幻溇、濮溇、汤溇，中西北湖区代表站包括长丰涧、大港、洪巷、官渎、社渎。

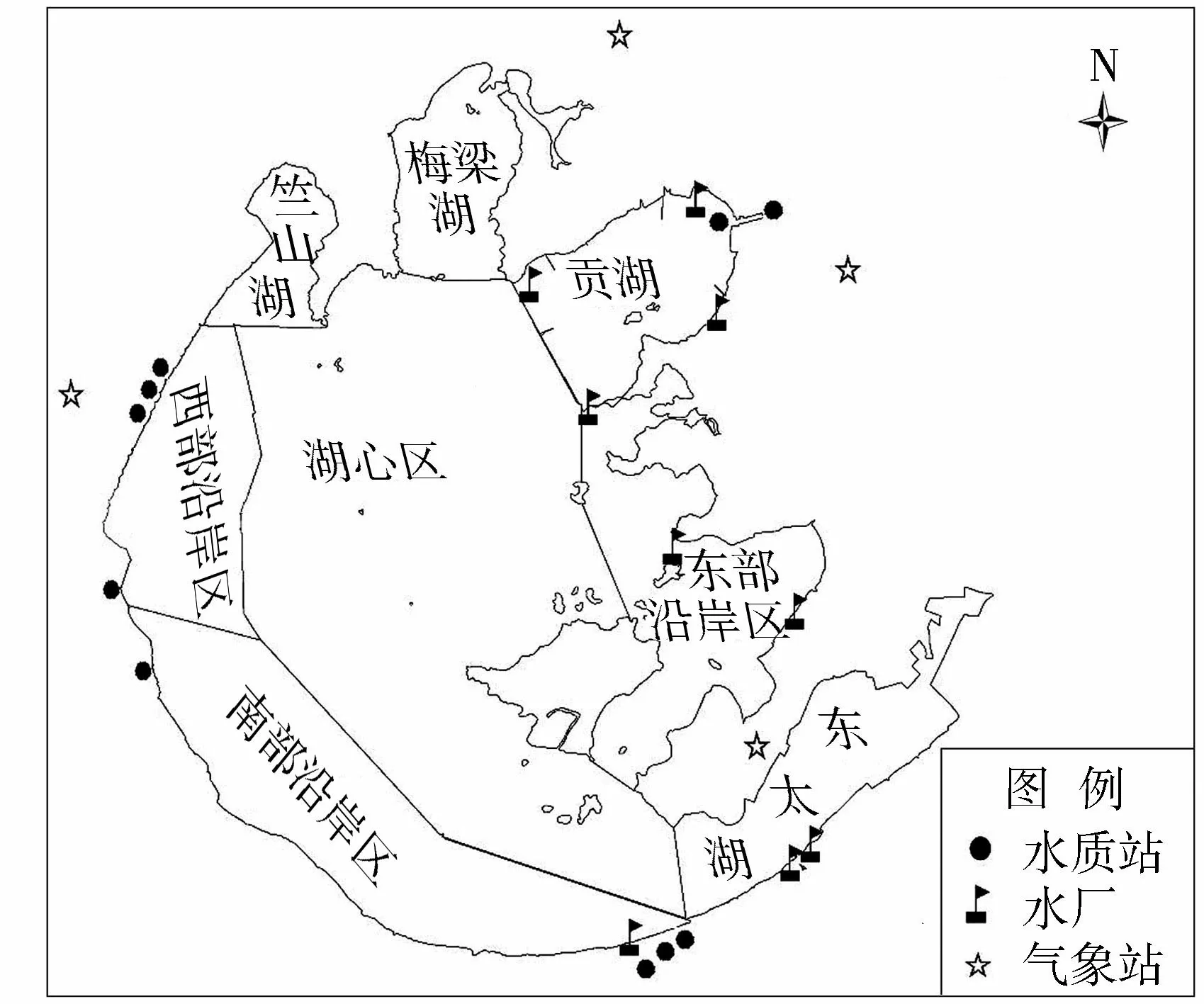
图1 太湖分区与观测站示意图Fig.1 Sub-regions in Taihu Lake and observation stations

1.2 研究方法

太湖藻华受物理、化学、生物因素等共同影响，机理十分复杂，呈非线性变化特征。本研究需要先采用Pearson 相关系数去除不相关或重复变量，提取对各湖区藻华面积影响较大的主要气象水文水质因子。从时间、空间尺度上考虑到不同湖区水质差异较大，MODIS成像时间为上午10：30左右，因此，从时间尺度上分成3个模型，模型1采用当天0：00—8：00之前的气象、水文、水质数据预测当天的藻华面积，模型2采用提前一天0：00—23：00的数据预测当天的藻华面积，模型3采用提前两天0：00—23：00的数据预测当天的藻华面积。由于SVM、LSTM、XGBoost模型既可解决分类问题，也可解决回归问题，并且处理非线性问题有一定的优越性，在水质评价与预测研究中有一定的应用情景，因此，本研究分别开展两类算法的应用研究，共建立24个模型。训练集、验证集为2014—2018年序列数据，其中随机抽取70%的样本(533组)用于训练，剩下30%的样本(228组)作为验证集。

1.2.1 数据预处理

由于输入变量可能不在同一个数量级上，数据之间的差异性可能对模型学习能力存在一定的不利影响，为了减少数值差异、保证模型参数稳定收敛，需要进行归一化处理，确保各变量处于相同的量级。

(1)

式中：X——输入变量；X′——变量X归一化后的值；Xmin、Xmax——X的最小值、最大值。

1.2.2SVM

SVM是通过核函数，将低维输入空间中线性不可分的点映射成高维特征空间中线性可分的点，通过划分超平面，使所有的点到分类超平面的距离最大化[34]。其中，高维空间中距离分类超平面最近的那些点所对应的低维空间点被称为支持向量[35]。核函数的作用是接受两个低维空间中的输入向量，计算出经过某种变换后二者在高维空间中的向量内积值，具体见文献[36]。

常用的核函数有线性、多项式、径向基、sigmoid核函数。经对比，本研究采用误差较小、分类准确率较高的径向基函数作为核函数[37]。SVM采用径向基核函数，相应参数为惩罚因子c和核参数g。为确定最佳的参数值，将c、g分别取以2为底的指数离散值，代入V折交叉验证法中，选取平均误差最小的c、g值；采用网格搜索法，减小取值范围和间隔，确定最佳参数，根据计算，最佳参数为c=0.76，g=0.38，V=5。

1.2.3LSTM

RNN属于深度学习方法[38]，用于处理非线性时间序列，但在实际建模中，存在梯度消失及梯度爆炸问题[39]。为此，Hochreiter等提出了LSTM，将RNN中隐含层中的神经元替换为记忆体，实现信息保留与长期记忆。通过记忆细胞进行状态信息存储，门结构负责细胞状态的更新与保持[40]。每个记忆体包含一到多个记忆细胞和3种“门”，包括“遗忘门”、“输入门”和“输出门”。 LSTM训练过程是寻找最优参数，使模型收敛、损失函数达到最小[41]。算法见文献[42]。LSTM 网络层中隐藏神经元数目是影响准确率的重要参数，为寻求模型的全局最优解，采用基于梯度下降、具有相当鲁棒性的ADAM自适应学习率优化算法；经计算，初始学习率取0.001，隐藏神经元数为256，可使全局最优。

1.2.4XGBoost

XGBoost模型为树结构，是对梯度提升决策树算法的改进，采用加法学习模型进行优化[43]。通过不断迭代生成新的树，加入子树使模型不断逼近样本分布，将多个分类准确率较低的树模型组合成一个准确率较高的模型[44]。通过在Xgboost损失函数中加入正则项，既控制模型的复杂度，也降低模型的方差，避免模型过拟合[45]。算法见文献[46]。XGBoost模型主要参数包括eta、subsample、max_depth。eta指学习速率，可以提高模型的鲁棒性；subsample指训练的实例样本占总体样本的比例；max_depth为树的最大深度，用来避免过拟合。经计算，最佳参数为eta=0.15，sub-sample=0.2，max_depth=8。

1.3 模型评价

常用评价指标包括：纳什效率系数(NSE)、相对偏差(PB)，公式如下：

(2)

(3)

NSE取值范围为负无穷至1，越接近1表示模拟效果越好、可信度越高；NSE接近0，表示模拟结果接近观测值的平均值水平，即总体结果可信，但过程模拟误差大。PB绝对值越小，模拟效果越好。

Pearson 相关系数(r)是描述两个随机变量线性相关的统计量，计算公式如下：

(4)

r取值范围为-1.0～1.0，越接近1.0，正相关越显著，越接近-1.0，负相关性越显著。构造统计量t检验相关性是否显著，计算公式如下：

(5)

统计量t遵从自由度ν=n-2的t分布。给定显著性水平α，查t分布表，若t>tα，认为相关系数是显著的。

2 结果与分析

2.1 相关性分析

为了确定所选气象、水文、水质因子对太湖藻华面积模拟的有效性，提高藻华面积模型的准确性，采用Pearson相关系数去除相关性不显著的变量。分别计算当天、提前1 d到提前30 d共计31种时间尺度条件下，全太湖、贡湖、南部沿岸区、中西北湖区藻华面积，以及气象、水文、水质数据之间的Pearson相关系数，发现当天、提前1 d、提前2 d时间尺度相关系数明显高于其他时段。Pearson相关系数较显著的因子如表1所示，全太湖藻华面积与水温、风速、降水等气象因子相关性较高，其中，与当天无锡2：00、8：00风速负相关性较显著，分别达到-0.17、-0.23。不同时间尺度下的贡湖藻华面积与水温、浊度、总氮、氨氮正相关性均较高，相关系数均可达0.15以上。南部沿岸区藻华面积与水温呈显著正相关性，相关系数均可达0.19以上，与当日东山站2：00、8：00风速呈显著负相关性。中西北湖区藻华面积与当日宜兴站2：00、8：00风速的负相关性较显著。

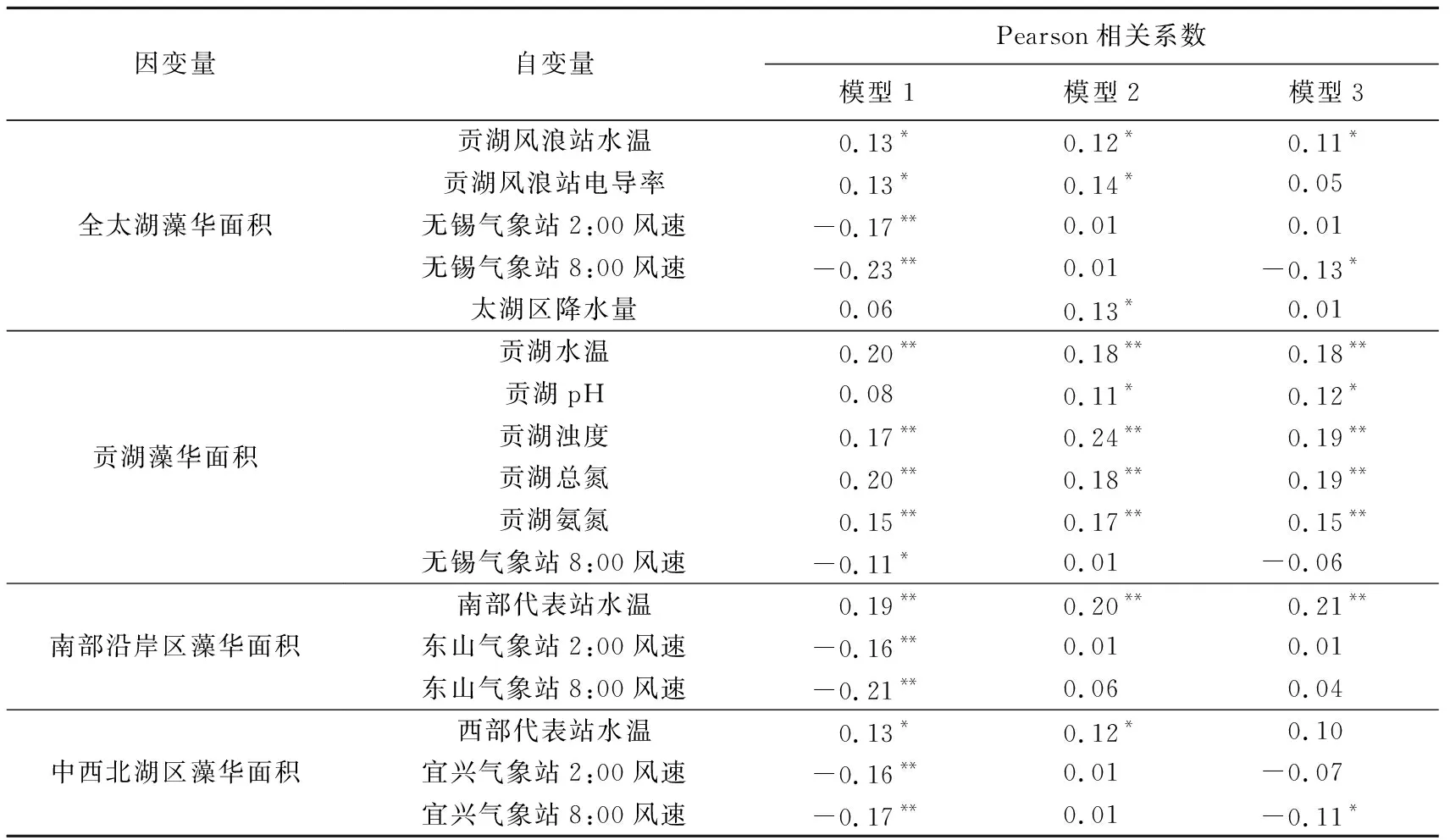
表1 藻华面积与气象、水文、水质因子之间的Pearson相关系数Table 1 Pearson relative coefficient between cyanobacterial bloom area and factors including meteorological, hydrological and water quality factors

2.2 模型分析结果

将训练集和验证集分别代入训练好的全太湖、贡湖、南部沿岸区、中西北湖区藻华面积模拟模型中，并对输出值进行反归一化处理。模拟值与观测值之间的NSE与PB见表2。对于不同时间尺度(当天、提前1 d、提前2 d)下的全太湖藻华面积回归模型训练集与验证集而言，XGBoost回归模型NSE最高、PB最低，其次是LSTM回归模型、SVM回归模型；验证期的XGBoost回归模型，当天的模型1与提前1 d的模型2，相对优于提前2 d的模型3。

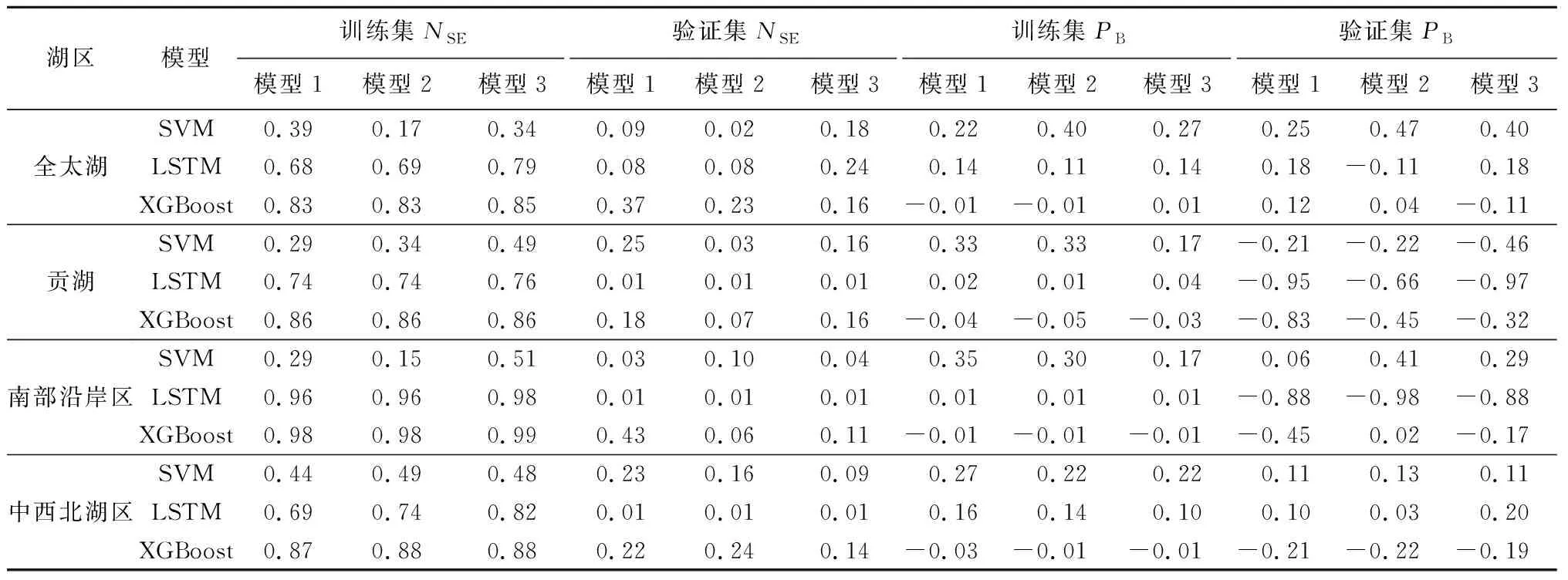
表2 3种机器学习回归模型评价结果Table 2 Evaluation results of three machine-learning regression methods

对于不同时间尺度下贡湖、南部沿岸区、中西北湖区的藻华面积回归模型NSE，XGBoost模型训练集与验证集NSE普遍较高，训练集LSTM模型的NSE高于SVM模型，验证集SVM模型的NSE高于LSTM模型；验证期的贡湖SVM模型：藻华面积模型1、南部沿岸区XGBoost藻华面积模型1、中西北湖区XGBoost藻华面积模型2的NSE高于相应湖区的其他时间尺度模型，与全太湖藻华面积回归模型表现也基本一致。

《太湖蓝藻水华评价方法(试行)》将蓝藻水华面积分为4类：<240 km2、[240，600)km2、[600，1 000]km2、>1 000 km2,相应面积水域发生水华分别称为零星湖区、局部湖区、区域、大范围水华暴发[47]。以全太湖藻华面积过程线拟合效果为例，分析SVM、LSTM、XGBoost回归模型模拟结果，见图2～4。模拟结果表明：不同时间尺度下SVM、LSTM回归模型训练集的模拟值偏低，XGBoost回归模型训练集模拟值与实测值基本接近；尽管SVM、XGBoost回归模型验证集模拟值较实测值偏小，但有效模拟了零星湖区、局部湖区水华的发展趋势；LSTM回归模型验证集的模拟值与实测值差异较大，不合理跳动较多，这也验证了神经网络模型存在过学习、泛化能力差的固有缺陷。

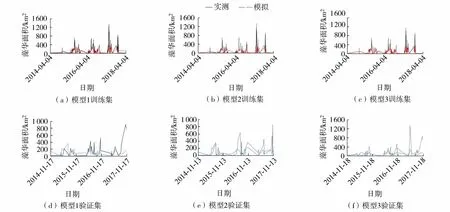
图2 基SVM于回归模型的全太湖藻华面积训练集与验证集模拟Fig.2 Training set and verification set simulations of cyanobacterial bloom area with SVM regression model in Taihu Lake

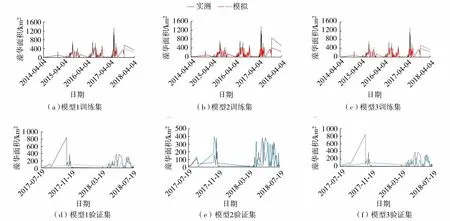
图3 基于LSTM回归模型的全太湖藻华面积训练集与验证集模拟Fig.3 Training set and verification set simulations of cyanobacterial bloom area with LSTM regression model in Taihu Lake

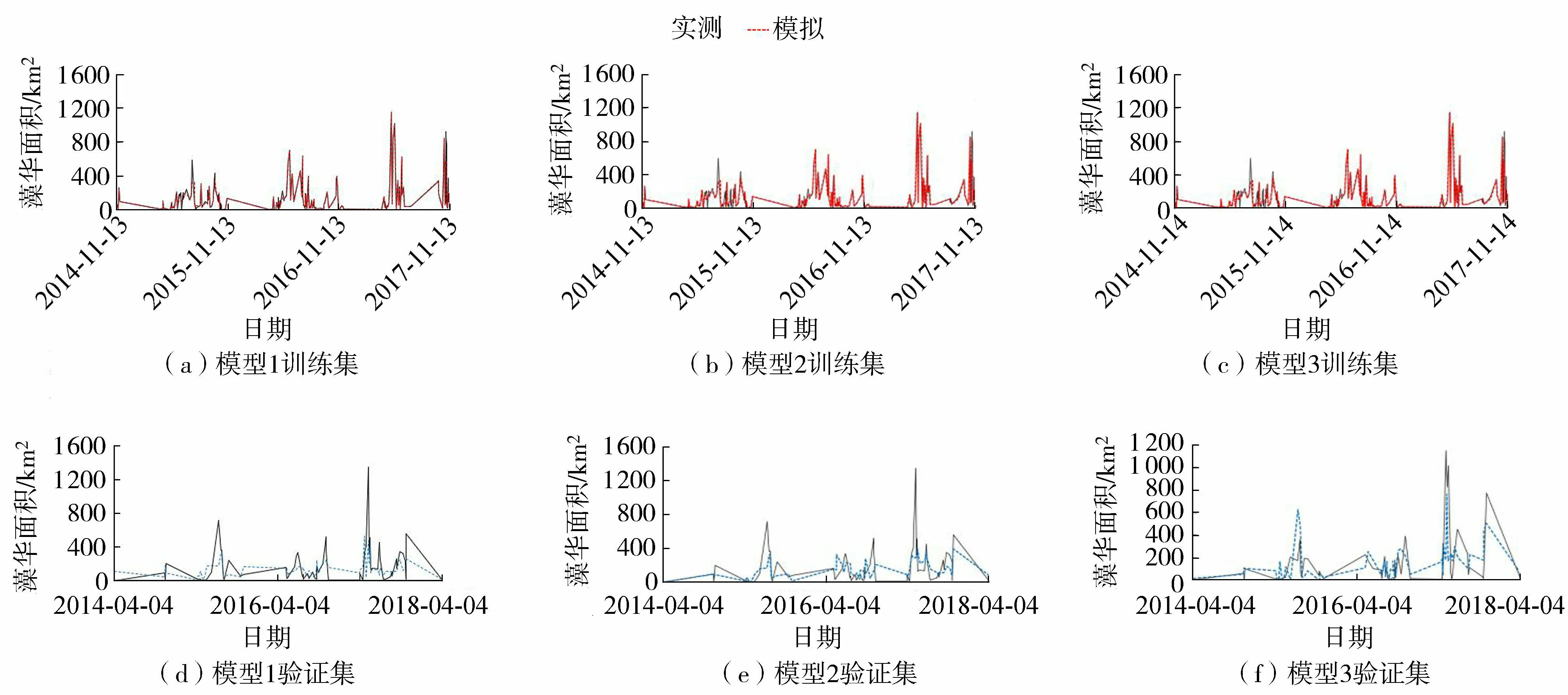
图4 基于XGBoost回归模型的全太湖藻华面积训练集与验证集模拟Fig.4 Training set and verification set simulations of cyanobacterial bloom area with XGBoost regression model in Taihu Lake

从上述分析可知，回归模型在验证期模拟效果不太好，考虑到藻华面积预测与防控业务中主要关注藻华面积与相应湖区面积比例的范围，对精确数值关注较少。为进一步改进藻华面积模型，采用分类算法输出离散的类别值。将藻华面积与相应湖区面积比例按照<10%、[10%，25%)、[25%，50%)、>50%分成4类，分析不同时间尺度下SVM、LSTM、XGBoost分类模型的正确率，见表3。表3结果表明：全太湖各模型的训练集正确率达到0.97以上，验证集SVM、XGBoost分类模型正确率达到0.80以上，LSTM分类模型正确率略低，为0.66～0.86，误差较大，见图5。贡湖各模型的训练集正确率达到0.89以上，验证集正确率达到0.82以上；南部沿岸区各模型的训练集正确率达到0.97以上，验证集正确率达到0.80以上；中西北湖区训练集正确率达到0.83以上，验证集XGBoost模型正确率达到0.80以上，好于LSTM分类模型、SVM分类模型。总体而言，贡湖藻华面积SVM、LSTM、XGBoost分类模型验证集正确率普遍优于其他湖区，可能与贡湖风浪站相对于其他环湖站点位置更加偏向于贡湖内部，气象、水文、水质数据代表性更强有关。

图5 不同时间尺度下SVM、LSTM、XGBoost分类模型的藻华面积验证集模拟Fig.5 Verification of cyanobacterial bloom areas with SVM, LSTM and XGBoost classification models in Taihu Lake

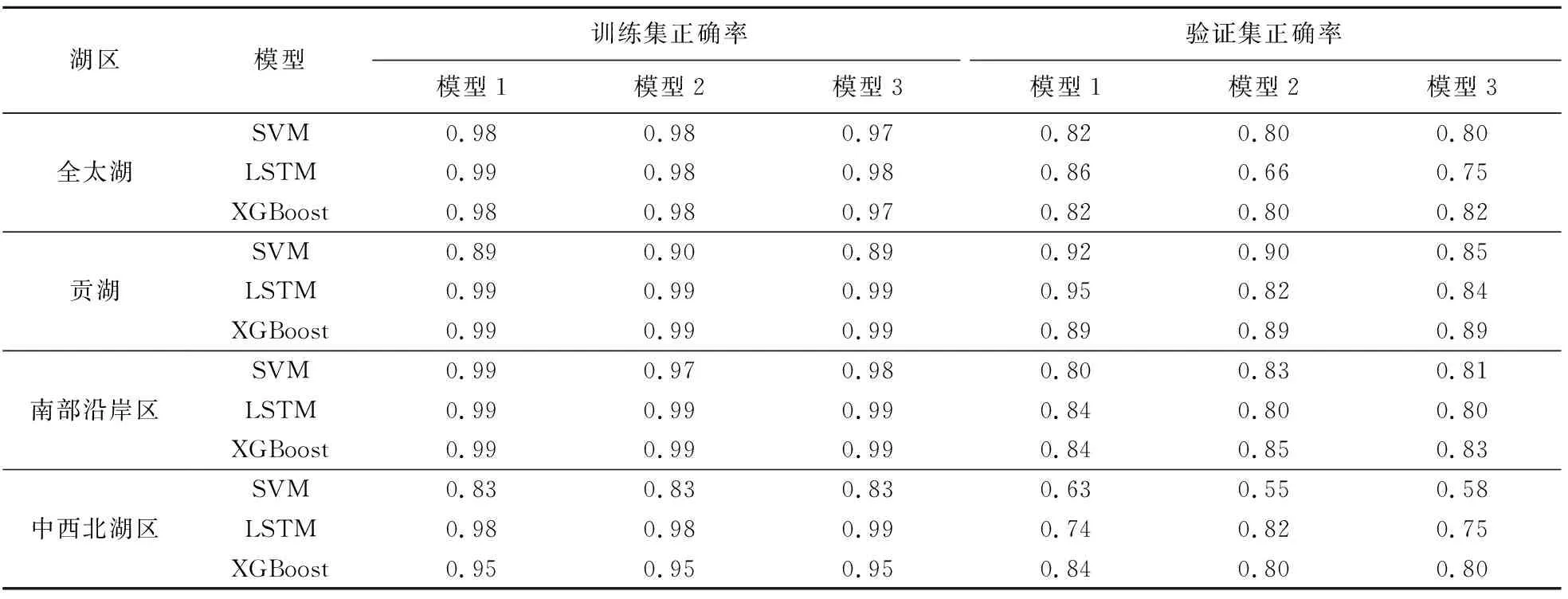
表3 3种机器学习分类模型评价结果Table 3 Evaluation results of three machine-learning classification methods

从上述研究可知，SVM、LSTM模型在藻华面积较低时，模拟与实测结果较接近；当藻华面积超过600 km2时，模拟与实测结果偏差较大。可能原因有3个：一是太湖藻华面积高值相对较少，且水华从暴发到消退较快，在运用机器学习方法训练模型时，如果目标值数量不均等、数值差异大，SVM、LSTM模型一般偏向于数量多、数值低的藻华面积的样本。二是LSTM较适合大数据的机器学习，在数据量足够多的情况下效果较优，而本研究的数据量可能远远达不到大数据的要求，LSTM无法很好地保证模型的泛化能力，存在陷入局部最优以及收敛时间长等问题[48]，导致模拟效果不佳。三是太湖风浪作用显著，适度的间歇性风浪扰动可以促进氮磷等营养盐释放，刺激蓝藻细胞生理特征改变，对太湖藻华迁移聚集影响较大，而模型只考虑了风场，流场数据的缺乏导致水动力输移考虑可能不够。总体而言，由于XGBoost模型在损失函数寻优过程中加入了正则项来控制过拟合现象，模拟藻华面积与实测相比，精度较高、稳健性较好。

3 结 论

a. XGBoost全太湖与分区的回归模型训练集与验证集模拟效果均较好，LSTM回归模型训练集较好、但验证集较差，SVM回归模型介于XGBoost与LSTM回归模型之间；SVM、XGBoost回归模型的验证集模拟值偏小，但有效模拟了藻华的发展趋势；选取当天、提前1 d的气象水文水质因子作为太湖及分区藻华面积模型的输入，模拟结果较好。

b. 在全太湖、中西北湖区藻华面积模拟中，XGBoost分类模型正确率较高；在贡湖、南部沿岸区藻华面积模拟中，SVM、LSTM、XGBoost分类模型正确率均较高。

c. SVM、LSTM模型在藻华面积较低时模拟与实测结果较接近，当藻华面积较高时模拟与实测偏差较大，可能与机器学习方法训练模型一般偏向于数量多、数值低的藻华面积的样本有关；XGBoost模型精度较高、稳健性较好，适合在太湖藻华面积预测中推广。