基于多因子最近邻抽样回归模型的径流相似性预报

谭乔凤，陈 然，朱 阳，胡立春，闻 昕

(1.河海大学水利水电学院，江苏 南京 210098； 2.国电大渡河流域水电开发有限公司，四川 成都 610041)

径流预报是防洪减灾、水资源保障、电力生产等流域管理和调度决策的关键依据，也是全球变化下水文水资源领域研究的前沿热点[1-2]。目前广泛运用的径流预报方法主要分为过程驱动和数据驱动两类[3]。前者从径流的物理成因出发，通过一系列含参数的数学物理方程描述产汇流过程，且每个参数都有明确的物理意义，但是当流域自然地理环境或产汇流条件复杂时，模型参数率定困难[4-5]；后者是以建立输入输出数据最优数学关系为目标的黑箱子方法[6-7]，无需考虑径流形成的物理机制，预报精度依赖于可靠且海量的样本数据[8]。

近年来，由于人工智能和大数据技术的快速发展，流域内现代化的水文测站网络的建立与完善，以及历史水文气象数据的积累，为突破径流预报瓶颈开辟了新思路和新途径。借助大数据技术，可对成千上万条历史数据实现全面、多层次的分析，隐藏于数字背后的水文规律可以“挖掘”出来。实际上，对于某一特定流域，在一定的地理环境条件下，制约降雨的主导天气系统和降雨类型会反复出现，在相似天气系统条件下所产生的降雨(或暴雨)过程及其径流(或洪水)过程也将是相似的。当具有较长时间、较多场次的历史降雨、径流过程时，采用数据挖掘技术，找出相似降雨-径流过程，“参考过去预测未来”，即根据历史相似降雨、径流提供的信息预测未来径流，这对延长径流预报预见期，提高流域水库群精细化管理及精益化调度水平具有重要意义。

1 径流相似性预报

1.1 多因子最近邻抽样回归模型

研究将基于实时降雨、历史降雨和径流的相似性特征，利用多因子最近邻抽样回归模型(NNBR)在历史降雨产流过程中搜索相似过程，预测后期径流过程。NNBR无需对研究对象的相依形式和概率分布作假定，能避免确定函数关系所带来的不确定性问题，是一类数据驱动的非参数模型[9]。其基本原理是：客观世界的发生发展存在一定联系，未来的运动轨迹与历史具有相似性，即未来发展模式可以从已知众多模式中去寻求。对于确定控制断面的径流预报，首先识别出与其相关性较高的前滞降雨、径流因子，建立降雨、径流特征指标矢量：

Xj=(X1,j,X2,j,…,Xp,j，Xp+1,j,Xp+2,j,…,Xp+q,j)

(1)

式中：Xj——预报因子；p——降雨特征指标个数；q——径流特征指标个数,共有m个特征指标，m=p+q。

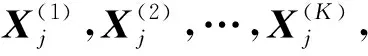
考虑到降雨和径流在数值量级上存在差异，引入降雨影响权重α，提出降雨、径流综合欧氏距离的计算公式：

(2)

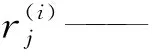
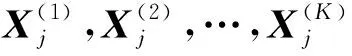
根据上述思想，用式(3)表示多因子NNBR的基本形式：

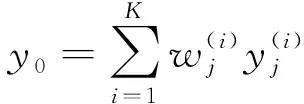
(3)

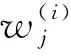
(4)

模型涉及的参数有：最近邻数、特征矢量维数、抽样权重、降雨影响权重。

a. 最近邻数K：模型根据已有的特征矢量，寻找历史中最近邻特征矢量的个数，也是模型的抽样个数。K的选取主要考虑两个因素：(a)降雨、径流的历史数据长度；(b)预报的径流量级在历史中出现的频率。首先根据历史数据长度预选一个最近邻数，当模型建立之后，测试不同K值下的预报效果，选取预报效果最好的值作为最终的K值。

b. 特征矢量维数：径流特征矢量维数由径流时间序列在不同滞时下的自相关性确定；降雨特征矢量维数需要结合降雨、径流物理成因，分析降雨与预报断面径流响应时间来确定，这个时间不仅与降雨量级有关，还与降雨中心的地理位置到预报断面的距离有关。

(5)

d. 降雨影响权重：研究结合遗传算法等现代启发式算法，以预报效果最优为目标，优化降雨影响权重α。其中，预报效果评价指标主要包括纳什系数(NS)、均方根误差(RMSE)、平均绝对误差(MAE)和平均相对误差(MARE)[10]。

1.2 滚动预报方式

为了延长预见期，实时接入滚动降雨预报信息，滚动预报未来径流过程，提出3种滚动预报方式。

a. 方式1：不考虑降雨预报和径流预报信息，直接根据已经发生的实测降雨和径流信息寻找降雨、径流相似过程，以预报t～t+f时段的径流过程为例。

(6)

b. 方式2：考虑降雨预报信息滚动更新降雨相似性，同时不断加入预报的径流作为输入滚动更新径流相似性以预报下一时段的径流。以预报t～t+f时段的径流过程为例：

(7)

c. 方式3：考虑降雨预报信息滚动更新降雨相似性，但是不将上一时段预报的径流作为输入，预测下一时段径流。

(8)

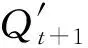
1.3 多模式自适应切换

针对流域在涨退水等不同阶段的产汇流特性，建立可根据实时水雨情自适应切换的降雨、径流输入模式，以进一步提高径流预报精度。例如，根据考虑前期降雨滞时长度的不同，分为短降雨滞时模式和长降雨滞时模式。短降雨滞时模式只考虑短期内的实测降雨，例如只考虑前1 d的降雨；长降雨滞时模式考虑更长时期内的实测降雨，例如考虑前3 d之内的降雨。短降雨滞时模式以退水期预报为主，长降雨滞时模式以涨水期预报为主，模型将根据前期径流、前期降雨、预报降雨等因素自适应切换预报模式。另外，历史库中不同量级径流出现频率不同，对于大量级洪水过程，历史上出现的相似降雨和径流过程较少，模型将对径流进行实时追踪，当径流数值到达某一个量级时，自动减小最近邻数以保证抽样样本具有相似性。

2 应 用 实 例

2.1 研究区域与数据

大渡河流域是国家规划的十三大水电基地之一，提高径流预报精度，延长预见期，对流域水库群精细化管理及精益化调度具有重要意义。本文以大渡河干流上游丹巴断面为研究对象。断面以上共有21个雨量遥测站点，3个流量站(绰斯甲、足木足、马尔康)，站点分布情况见图1。为降低模型的输入维度，将预报断面以上的流域降雨站点分为5个子区域，并建立各分区点雨量到面雨量的空间映射关系，在体现流域降雨空间分布格局的前提下降低降雨数据输入维度。区域1包含色达、壤塘、一林场3个雨量站；区域2包含班玛、灯塔2个雨量站；区域3包含俄热、太阳河2个雨量站；区域4包含日部、草登、足木足、马尔康、刷经寺5个雨量站；区域5包含丹东、边尔、布科、东谷、沙冲、牦牛、抚边河、小金、达维9个雨量站。研究收集了各站点2008—2019年的逐日历史实测降雨、径流资料，并以2008—2016年的数据构建历史降雨、径流样本，对2017—2019年的径流进行相似性预测，以评价模型未来1 d和未来7 d逐日的预测效果。

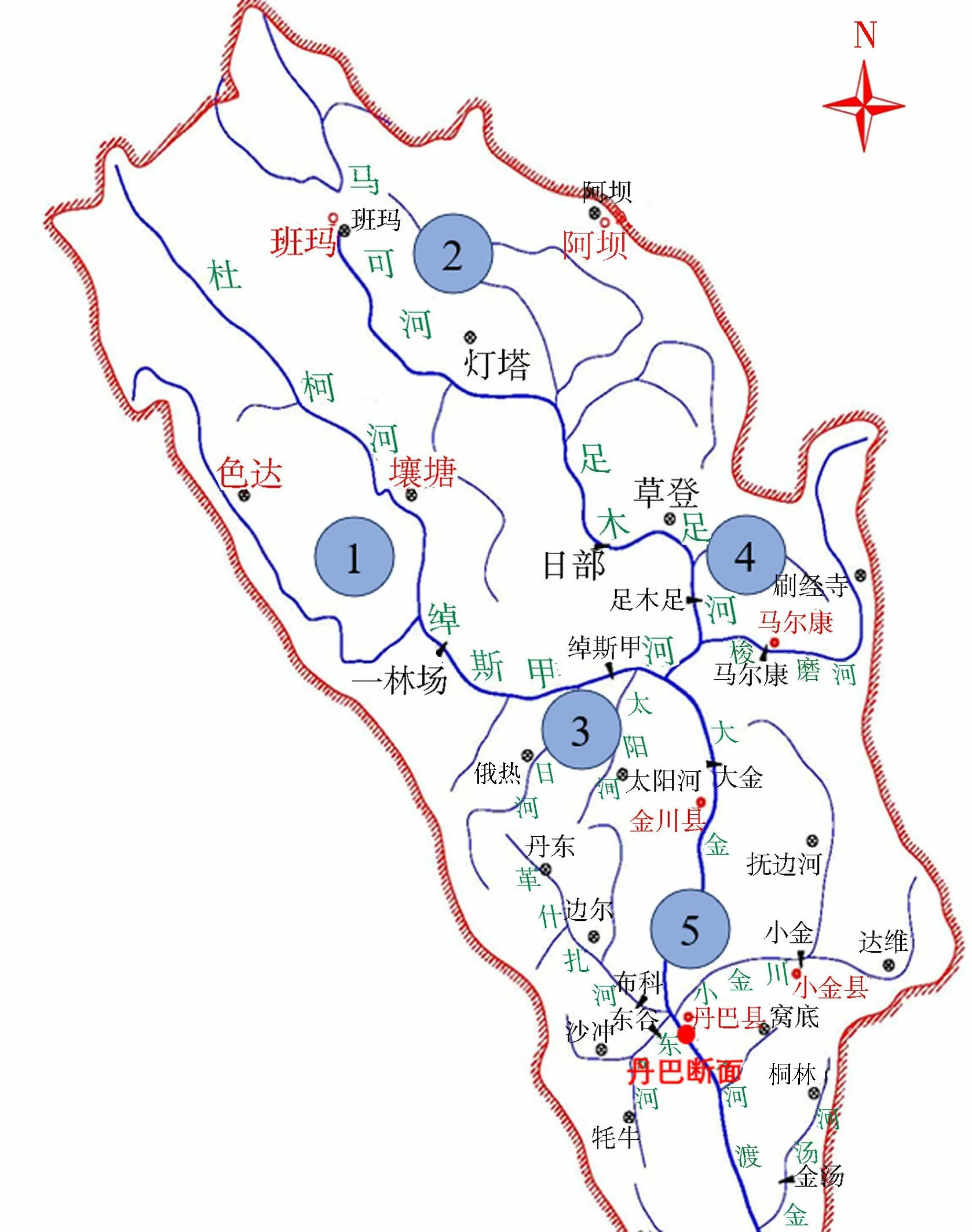
图1 大渡河流域丹巴以上水文站点分布Fig.1 Distribution of hydrological stations above Danba in Dadu River Basin

2.2 未来1 d预报

2.2.1 预报方案设置

预见期为1 d的预报因子分为3类：上游雨量(点或面雨量)、上游径流、丹巴本站径流。根据相关性分析，上游前1 d雨量与丹巴径流相关性最高，因此可以初步取降雨滞时为1 d。丹巴径流自相关系数在前5 d分别为：0.96、0.87、0.79、0.69、0.61。前4 d滞时下的相关性系数明显下降，因此丹巴本站前期径流滞时取3 d。另外，研究测试了预报结果为绝对值和相对值两种输出模式。绝对值模式根据相似性样本下一时段径流的绝对值预报实时径流；相对值模式根据相似性样本下一时段径流相对于前一时段径流的变化量预报实时径流。

根据不同的输入因子和输出模式，研究设置了多种预报方案，如表1所示。其中，方案1～4采用绝对值模式，方案1与方案2是为了对比点雨量和面雨量输入对预报效果的影响。方案3与方案2是为了对比上游支流站点径流对预报效果的影响。方案4的预报因子只考虑丹巴本站前期径流，可测试只考虑径流自身时间序列的预报效果。方案5～10采用相对值模式，6种不同滞时组合下预报方案形成对比。值得注意的是，方案5与方案2的预报因子输入完全相同，但是方案2采用绝对值模式，而方案5采用相对值模式，因此这两种方案可直接对比2种输出模式的预报效果。

表1 未来1 d的预报方案Table 1 Forecast schemes with foreseen period of 1 day

2.2.2 预报结果分析

方案1～10的预报精度评价结果见表2。从表2可知，采用面雨量输入的方案2各项指标均优于采用点雨量输入的方案1。采用相对值输出的方案5～10的预报效果整体优于采用绝对值输出的方案1～4，因此预报模型输入取面雨量、输出取相对值更适合本案例。方案2与方案3的精度对比可知，是否考虑前1 d上游3站的径流对丹巴预报效果影响不大。与方案3相比，方案4的预报精度明显降低，说明前期降雨对丹巴径流影响显著。方案5～10共6种预报方案的预报效果整体接近，在NS等于0.96的方案7～9中，方案7的RMSE虽然比方案8、方案9略高，但是MARE最低，因此确定方案7是预见期1 d的最优方案。

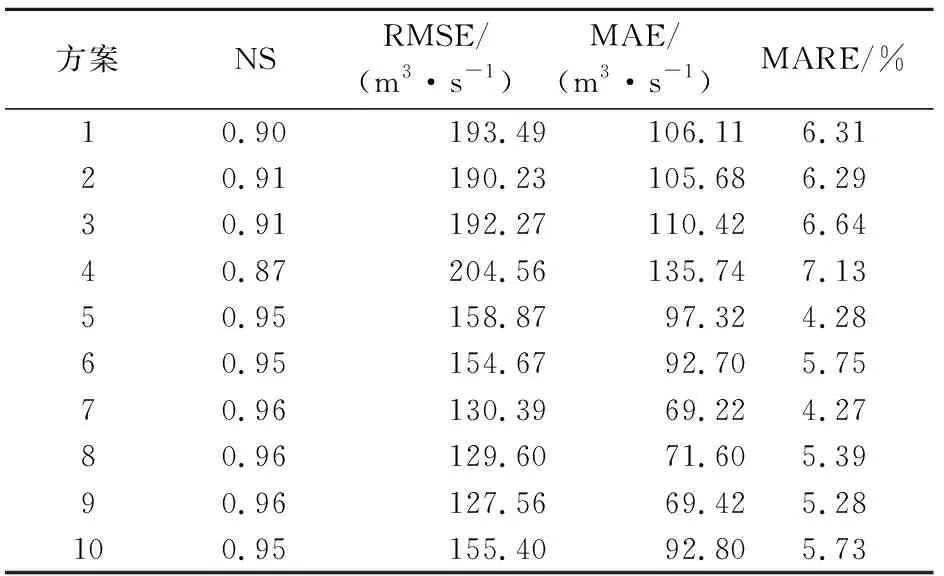
表2 预见期为1 d的预报精度评价Table 2 Forecast accuracy with foreseen period of 1 day

从2017—2019年3 a的预报结果来看，当预见期为1 d时，模型的整体预报精度较高，但是在个别洪峰处的预报效果较差。以2018汛期(5—10月)为例(图2)，在年最大洪峰处的预报值明显低于实际值，可能的原因有两个：一是NNBR的预报结果是历史相似样本的加权平均值，容易出现极大值预报偏小和极小值预报偏大的情况；二是历史相似的大量级洪水场次较少，导致模型抽样得到的样本相似性较弱。

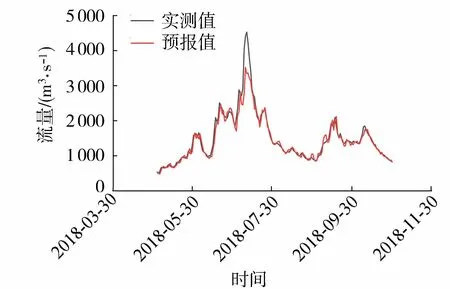
图2 预见期为1 d的预报结果Fig.2 Forecast results with 1-day forecast period

2.3 未来1周预报

2.3.1 预报方案设置

为了延长径流预报预见期，实时接入7 d降雨预报信息，预报流域未来1周的径流过程。由于缺失历史降雨预报资料，用实测降雨代替降雨预报信息。在预见期为1 d的预报方案基础上，提出3个滚动预报方案。3种方案的预报因子均是上游5个区域前1 d面降雨和丹巴本站前3 d、前2 d、前1 d径流，并且均采用相对值输出模式。3种方案分别对应章节1.2所介绍的3种滚动预报方式，具体方案如表3所示。

表3 预见期为7 d的滚动预报方案Table 3 Forecast schemes with foreseen period of 7 days

2.3.2 预报结果分析

滚动预报方案1～3的预报精度见表4。滚动方案2在7 d内预报效果最好，滚动方案1与滚动方案3的预报效果很接近。且随着预见期的增加，预报精度显著下降。图3显示了滚动方案2对2019年汛期典型洪水的预报过程图，黑色线为实测径流过程，每一个日期图例表示以该日期为预报起点的未来7 d的径流预报过程，预报结果逐日滚动更新。典型径流过程的预报结果与实测值较为接近，整体预报精度较高。

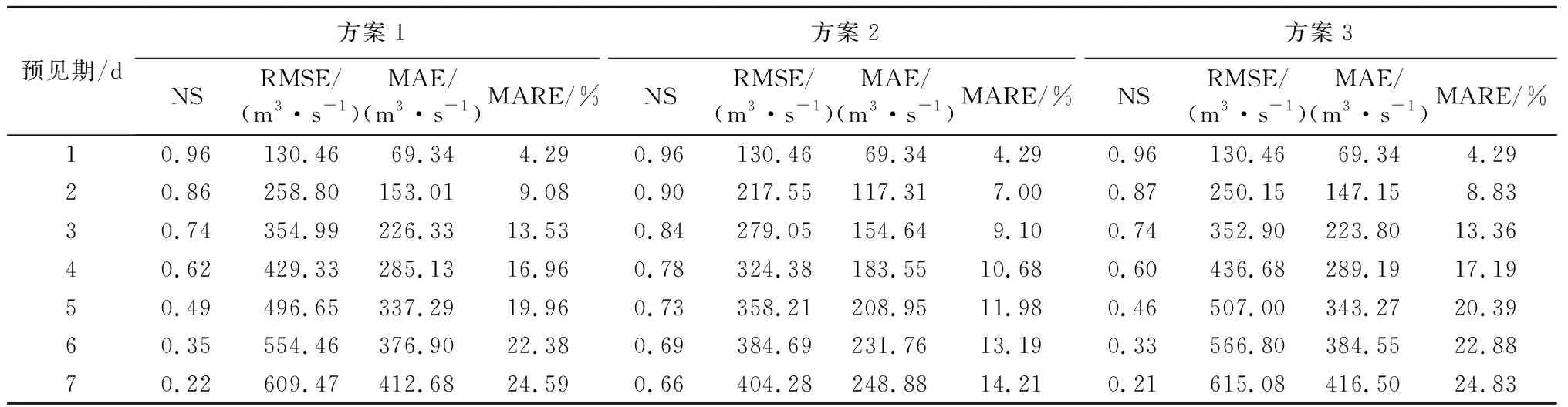
表4 预见期为7 d的预报精度评价Table 4 Forecast accuracy with foreseen period of 7 days

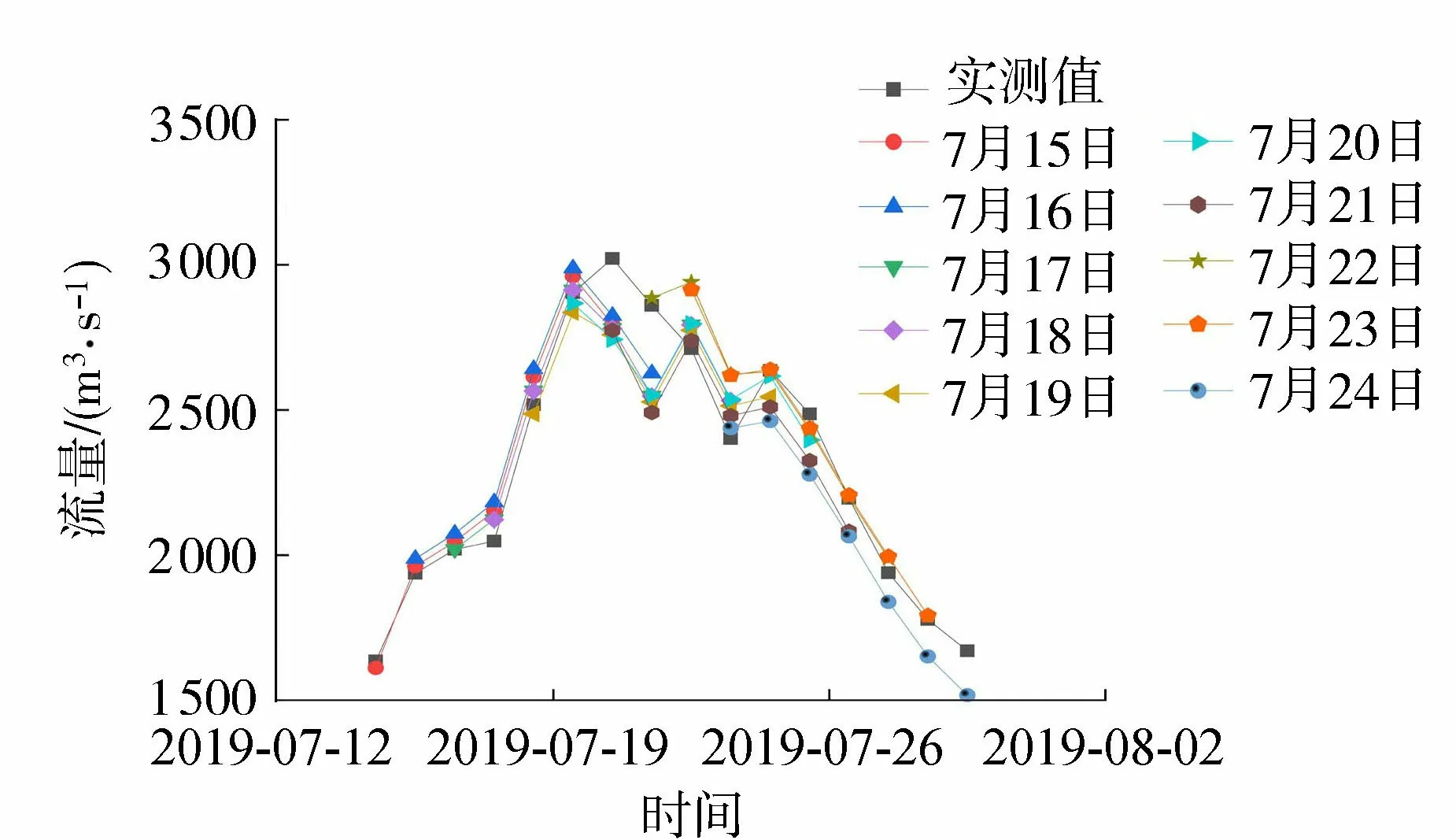
图3 典型洪水过程的滚动预报结果Fig.3 Rolling forecast results of typical flood

2.4 多模式自适应预报

在进行未来1周径流预测时发现当前1 d的降雨Pt-1延长至前3 d降雨Pt-3,Pt-2,Pt-1时，能够更好地预测大渡河丹巴断面的汛期涨水过程。通过分析Pt-1和Pt-3,Pt-2,Pt-1两种输入的滚动预测效果，研究确定了模型自适应判断条件，当满足判断条件时，模型将从1 d模式切换至3 d模式；否则，默认采用1 d模式进行滚动预报。同时，研究发现，当前期径流量级超过3 500 m3/s时，应适当减少最近邻数，推荐取4。

采用多模式自适应切换对2017—2019年的滚动预报效果见表5。总体精度相比于原滚动方案2有显著提升。预见期为3 d的NS大于0.9，MARE小于10%；预见期为7 d的NS大于0.8，差MARE小于15%。与原滚动方案2相比，在径流发展的不同阶段自适应预报效果均有提升，其中涨水阶段的预报效果提升最为明显(图4)。自适应预报带来的精度提升主要源于最近邻样本相似性增强和累计误差的减小。通过判断当前降雨、径流状态，选择不同的预报模式寻找相似性样本，可以有效提高预报精度，减小累计误差。

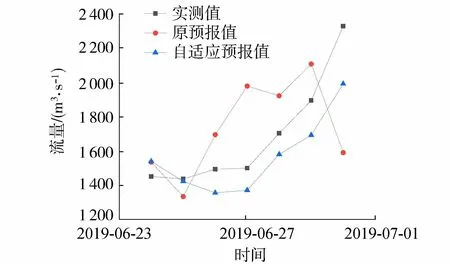
图4 典型径流过程的自适应预报结果Fig.4 Adaptive forecast results of typical runoff

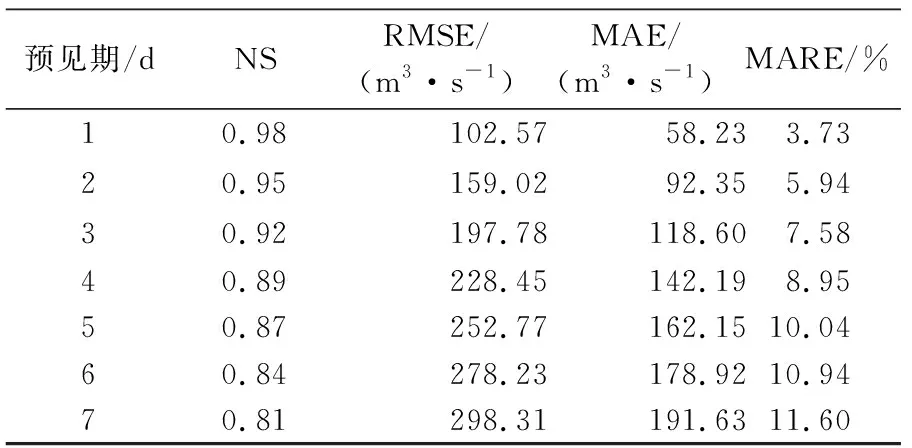
表5 自适应模式的预报精度评价Table 5 Forecast accuracy of adaptive mode

3 结 语

基于多因子最近邻抽样回归模型开展径流相似性预报，预报效果整体较好。同时，针对流域在涨退水等不同阶段的产汇流特性，建立可根据实时水雨情自适应切换的降雨、径流输入模式，进一步提高了径流预报精度。在大渡河丹巴断面的应用效果表明预报效果达到预期，3 d预见期的NS大于0.9，MARE小于10%；7 d预见期的NS大于0.8，MARE小于15%。未来可以对洪峰处的径流过程做进一步深入研究，优化不同应用环境下的模型参数，优选特定径流过程的相似性样本，全面提升径流预报精度。