波流作用下破波带内污染物输移扩散试验

郁 重,任春平,2

(1.太原理工大学水利科学与工程学院，山西 太原 030024；2.天津大学水利工程安全与仿真国家重点实验室，天津 300072)

波浪传播到近岸区后由于水深减小，发生浅水变形，引起波高增大，当某点的波高大于该点的最大破碎波高时，该点波浪发生破碎，一般将波浪从开始破碎到静水线的范围称为破波带[1]。近年来随着沿海经济发展，由于破波带毗邻海岸，导致该区域内沿海企业排污等海洋环境问题愈加严重，同时破波带也是许多生物种群的活动区域[2]。因此，对破波带内污染物输移扩散特性的研究尤为重要。

破波带内波浪破碎的同时除了水体紊动还会产生平行于海岸的单向水流——沿岸流[3]，因而沿岸流也是破波带内污染物输移扩散的主要研究方面，近半个世纪以来对于破波带内污染物扩散已有诸多研究成果。许多学者利用示踪剂(rhodamine或其他染料)来研究破波带内污染物输移规律并测量海岸扩散系数[4-11]。

Harris等[4]、Inman等[5]、Clarke等[6]通过定点测量示踪剂浓度及Fick溶液扩散律拟合等方法得到的破波带内垂直岸线及沿岸方向的污染物扩散系数范围在10-3～104m2/s范围内。Satoshi等[10]利用现场系泊视频系统观测破波带内示踪剂的时空变化来分析污染物的输移扩散特性。Clark等[11-12]通过现场试验研究了污染物在破波带内垂直岸线方向上受涡流及剪切波影响的对流特性。Kumar等[13]利用物理模型研究了破波带内斯托克斯漂移和瞬时裂流对水体表面污染物输移的影响。

部分学者通过建立数学模型对破波带内污染物输移扩散特性进行探究。Spydell[14]基于Boussinesq模型定量分析了破波带内正常入射波和斜向入射波的扩散系数。Hsu等[15]建立了基于浅水和缓坡地形的二维沿岸流模型，分析了近岸地形和湍流效应对破波带内流速场的影响。Spydell等[16]通过现场试验建立了假设初始参数的拉格朗日随机模型来估计垂直岸线方向及沿岸方向的扩散系数。孙涛等[17]用物理模型试验和数学模型计算相结合的方法，研究了均匀缓坡岸滩上，规则波及不规则波作用下形成的沿岸流及其对岸边排放污染物输移扩散的影响。邹志利等[18]进行了在规则波作用下测量破波带内水平混合系数的物理模型试验，通过在沿岸流场中投放墨水点源测量其扩散过程，并利用水深平均二维扩散方程近似解析解得到了计算混合系数的方法。

上述现场试验由于不可控因素较多，并且大部分扩散过程为点源扩散，进行的试验还不能代表破波带内的情况，因而有必要通过试验对破波带内污染物输移扩散特性做进一步的研究。本文通过物理模型试验及图像分析对破波带内不同波况作用下的污染物输移情况及垂直岸线方向的扩散系数进行分析，着重讨论波浪破碎产生的沿岸流及旋涡导致的污染物输移扩散运动的变化特点，总结变化规律，并估计污染物扩散系数。

1 试 验 简 介

试验在大连理工大学海岸和近海工程国家重点实验室的多功能综合水池内进行，水池长55.0 m、宽34.0 m、深1.0 m。海岸模型与造波板成30°角放置，以增加海岸线的长度。在水池上下外壁设置了波导墙(内壁处设有消浪网)，水流可在外部形成循环(图1，箭头方向为水流方向)，通过模拟可得到真实的沿岸流场。在垂直岸线方向设置2列共32个电阻式流速仪来测量沿岸流速度，流速仪端部与水底的距离为水深的1/3以测量沿岸流沿水深的平均值。

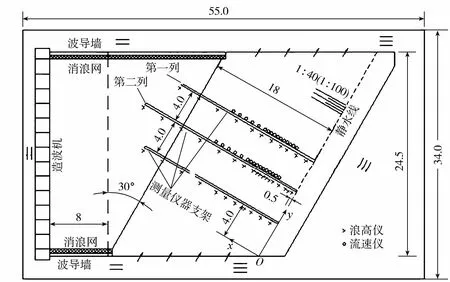
图1 试验布置(单位：m)Fig.1 Experimental setup (units: m)

试验采用1∶100坡度的平直斜坡海岸模型(图2)，入射波浪为多组规则波斜向入射(30°角)，针对规则波波高及周期参数不同，试验分为5组工况进行，波况参数见表1。

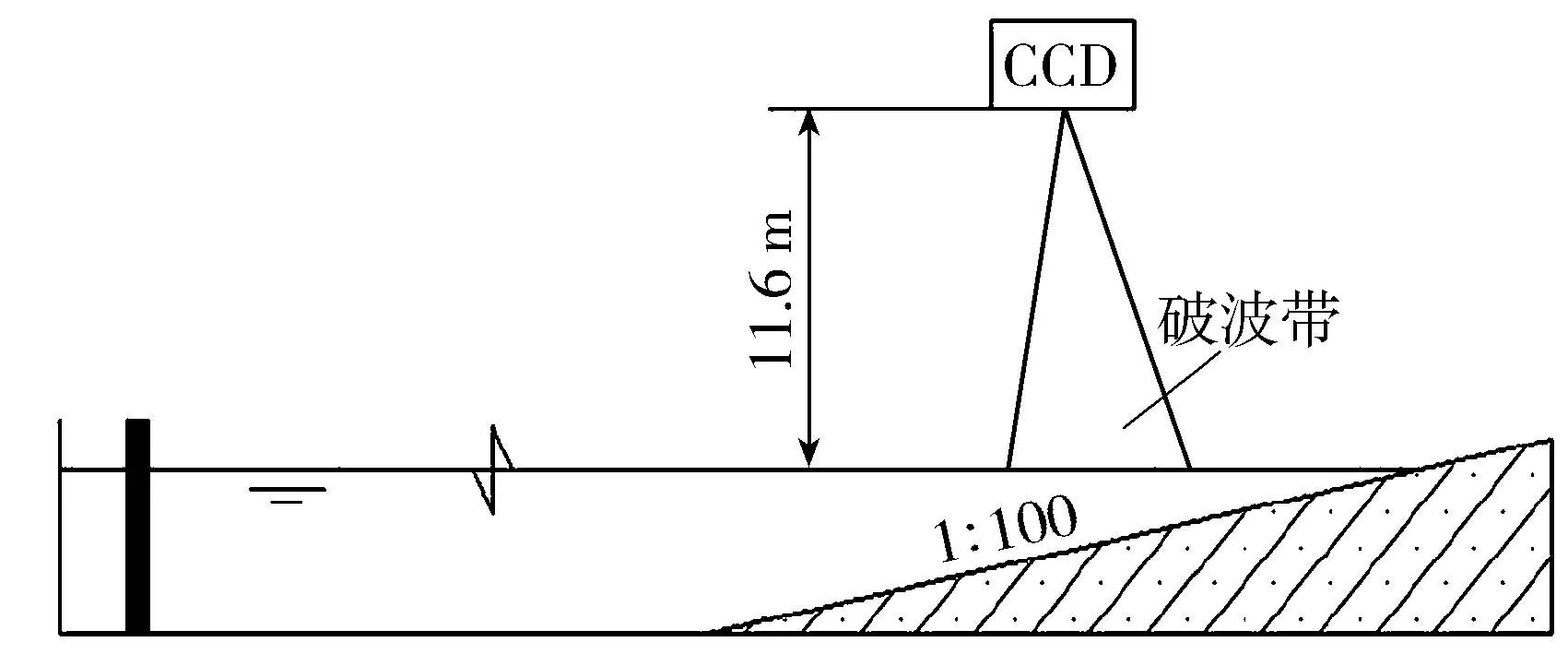
图2 污染团采集系统示意Fig.2 Acquisition system of pollution mass

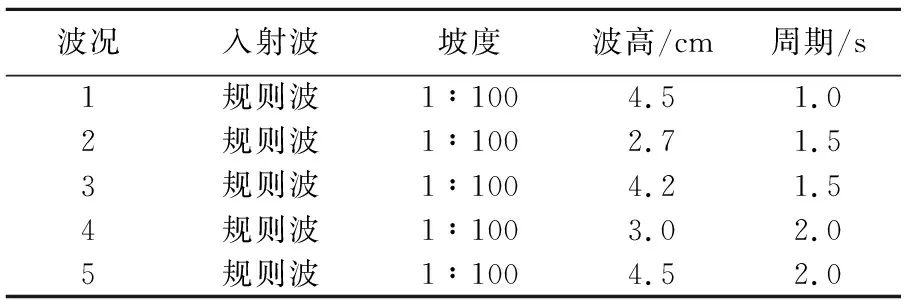
表1 波况参数Table 1 Wave parameters

试验通过在水体中投放墨水的方法来模拟近岸污染物的运动，选取波浪破碎点为污染物排放点，规则波入射时排放点坐标为(3.0 m，4.5 m)，墨水的排放形式采用连续源排放。试验图像利用摄像装置CCD采集，再通过图像采集卡DT3155进行转换，形成计算机可以存取的图像文件。图3给出了试验中波况2拍摄得到的部分墨水运动轨迹，从图3中可以看出，墨水随时间的输移变化可以被清晰记录。

图3 波况2采集的t=20 s、25 s、30 s、35 s、40 s、45 s时污染团结果Fig.3 Measured results of pollution mass for case 2 at t=20 s, 25 s, 30 s, 35 s, 40 s and 45 s

2 图像处理方法

在造波机制造的规则波稳定后连续投入墨水，分别获取不同波况下每秒的墨水团扩散图像，同时取波况1～5墨水开始投入时的图像为各个波况的背景图。受到试验场地的限制，在排放点污染物浓度会存在一定的累积效应，因此在开始处理图像时，需要在采集到的每秒图像中减去各波况污染物排放时的背景图像。以下取波况2中墨水投入后第45 s时的墨水团图像来介绍分析方法。图4给出了图像处理流程。

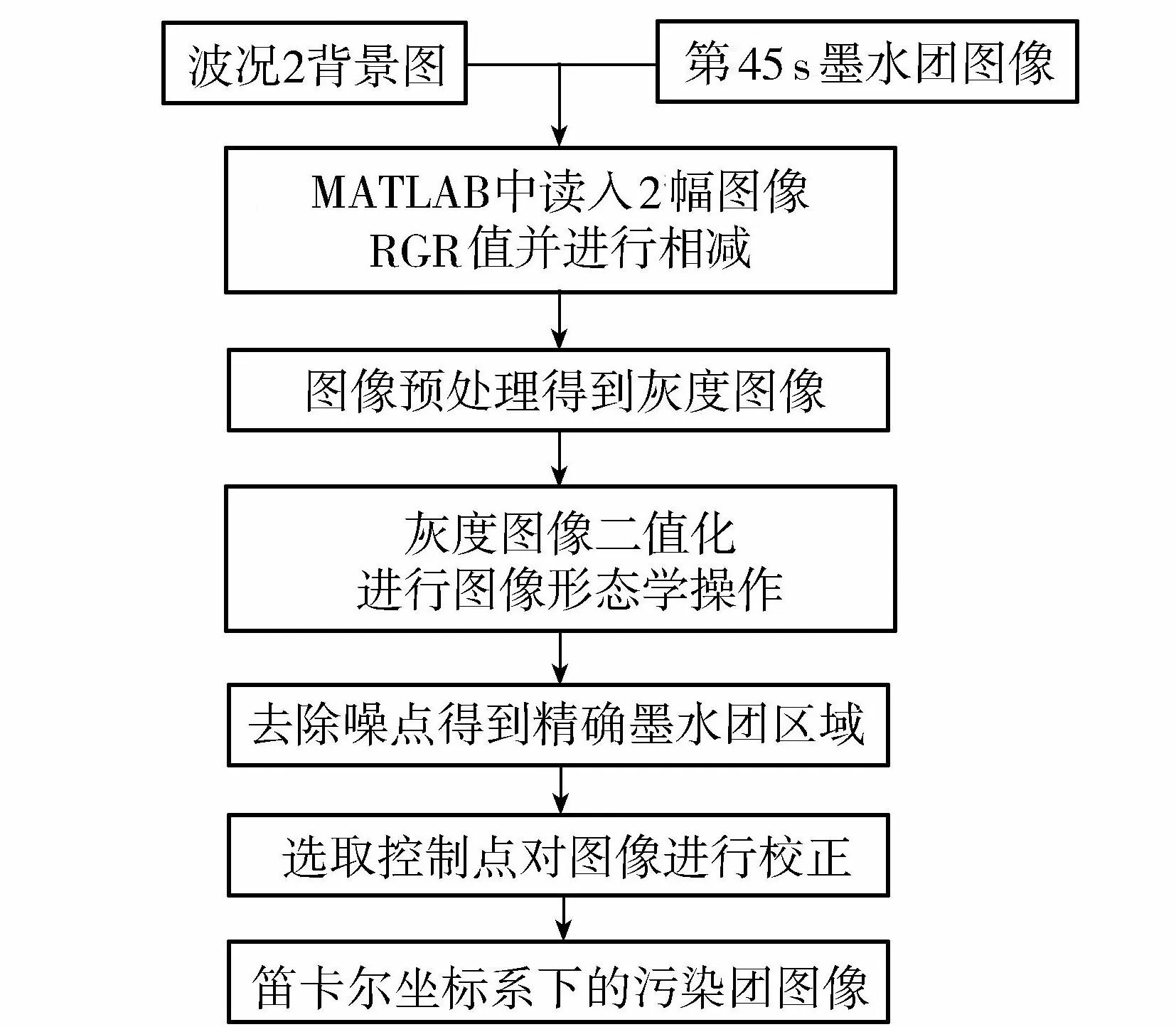
图4 图像处理流程Fig.4 Flow chart of image-processing steps

通过CCD摄像机获取的图像像素都为752×576，对应试验场地的物理坐标为7 m×5 m，图像的像素坐标与物理坐标一一对应。由于墨水团区域需在笛卡尔坐标系中进行分析计算，但试验中采集图像的CCD摄像头视点与水体表面存在仰角，需要对上述得到的墨水团区域进行畸变校正。在波况2获得的图像中选取30组物理坐标及与其对应的30组像素坐标作为控制点(图5)，采取从控制点到生成空间变换结构的仿射变换形式作为校正方法对图像进行处理，校正后对该图像进行二维空间变换得到图6，即为笛卡尔坐标系下的污染团图像校正结果。

图5 校正采用的物理和像素坐标Fig.5 Physical and image coordinates

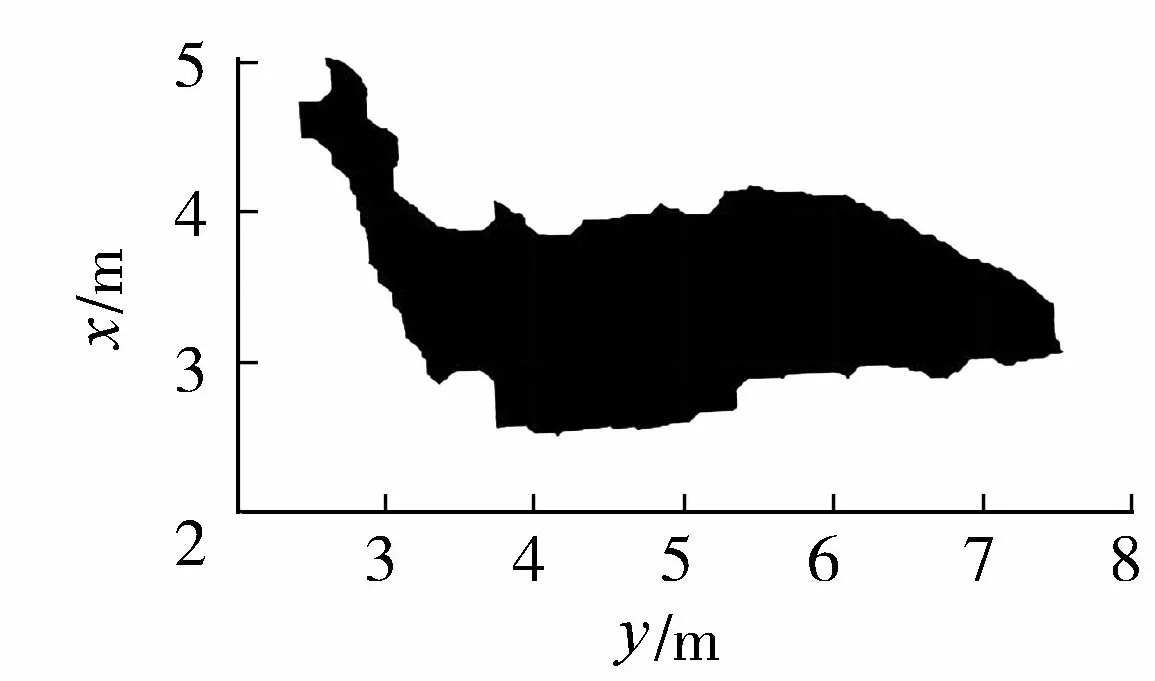
图6 图像校正后结果(t=45 s)Fig.6 Transformed result of image at t=45 s

3 污染团输移扩散特性

3.1 获取污染团形心点及离散程度

校正后的污染团图中有黑、白、灰3种颜色，其对应的像素值分别为0、255、200。定义像素阈值函数g(u,v,t):

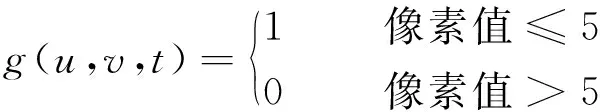
(1)

式中：u、v——像素坐标；t——墨水投入后经过的时间。利用该函数确定污染团范围。

用参数Xc(t)、Yc(t)表示某一时刻污染团形心点坐标，用σx(t)、σy(t)表示污染团x、y方向离散程度，具体见图7。某一时刻污染团形心点坐标Xc(t)，Yc(t)的计算公式如下：

图7 污染团分布特征参数示意图Fig.7 Distribution characteristic and parameters of pollution mass

(2)

(3)

式中：N——校正后图像内污染团区域像素点个数；x、y——校正后图像内污染团区域像素点的物理坐标。

污染团在x、y方向的离散程度σx(t)和σy(t)用以下公式计算得到：

(4)

(5)

3.2 污染团输移速度分析

由于不同波况下污染物输移的速度及方向不同，且图像采集范围是固定的，故不同波况在该范围内的有效采集时间及图像数量不同。波况1～5对应的有效采集时间分别为38 s、60 s、40 s、36 s及38 s。利用上述图像处理方法对采集到的图像进行处理可得到5种波况每秒图像的污染团形心点及离散程度，图8给出了波况1～5污染团形心点随时间在沿岸和垂直岸线方向的位移变化，并对位移与时间的变化进行了线形拟合，进而确定5种波况中污染团在2个方向上的输移速度。

图8 波况1～5污染团形心点在沿岸和垂直岸线方向输移结果Fig.8 Transport results of pollution mass centroid in the alongshore direction and the cross-shore direction for Case 1 to Case 5

图9给出5种波况下污染团分别在垂直岸线方向和沿岸方向的输移速度对比。可以看出在垂直岸线方向上5种波况污染团输移速度并不一致，其影响因素可能有以下几种：(a)波浪在向岸边传播过程中波峰线与海岸线并不平行，接近岸边时深度变浅导致波浪破碎，波浪破碎的同时能量分解引发垂直岸线方向波流紊动从而影响了该方向的输移速度；(b)由于波浪的非线性使水质点的运动轨迹不封闭而引起的质量输移流，质量输移流表现为水流紊动，由于惯性其方向近似垂直于岸线，并对破波带内物质在垂直岸线方向的输运起主要作用；(c)在波浪破碎时可能会导致流体产生有旋运动从而影响波浪表面污染团的输移速度。在沿岸方向上5种波况污染团的输移速度基本一致，主要原因是该方向水体表面污染物输移的主要影响因素是沿岸流，而波的作用相对可以忽略不计。

图9 波况1～5垂直岸线方向和沿岸方向输移速度对比Fig.9 Comparison of transport velocities in the alongshore and cross-shore directions for Case 1 to Case 5

表2给出了5种波况下污染团垂直岸线方向和沿岸方向的输移速度的关系与沿岸方向输移速度和时均沿岸流速最大值的关系。比较波况2与3、波况4与5，可以看出在周期一致的情况下，时均沿岸流速最大值随着波高的增大而增大；比较波况1与3、波况2与4，在波高接近的情况下，但时均沿岸流速最大值随周期的增大而减小，由此说明在规则波入射情况下时均沿岸流速最大值随波高增大而增大，随周期增大而减小。不同波况下时均沿岸流速差异明显，但污染团在沿岸方向的输移速度却基本一致，其原因一方面可能是由于沿岸流速沿水深并不是均匀分布的，在规则波入射情况下，波浪沿垂直波峰线方向传播到破波带时破碎程度不高，水体紊动并不剧烈，各水层间混合不明显，试验中将流速仪置于距床底水深1/3处来测量某点沿岸流速[19]，进行时均后将其作为该点不同水深处的流速平均值，而污染物则主要受到水体表面流速影响发生输移扩散，其大小与时均沿岸流速并不一致，导致污染团沿岸方向的输移速度与时均沿岸流速存在差异；另一方面试验中规则波为斜向入射，波浪破碎的同时在垂直岸线及沿岸方向的分解引发的波流紊动也会影响2个方向上污染团的输移速度。

表2 污染团输移速度与时均沿岸流速的关系Table 2 Relationship between the transport velocity of pollution mass and time-averaged longshore current velocity

破波带内水动力特性异常复杂，在分析沿岸方向污染物输移扩散特性时需将离散及扩散作用的影响区别讨论。由表2中可以看出，各波况垂直岸线方向的输移速度约为沿岸方向输移速度的10%～50%，这是由于污染物在破波带内沿岸方向上不仅有扩散，还存在离散，而且在沿岸方向对流对污染物输移的影响要远大于垂直岸线方向波的影响。沿岸方向的输移速度约为时均沿岸速度最大值的27.9%～40%，并且变化幅度不大，说明在沿岸方向对流作用是波浪表面污染物输移的主要动力因素。

通过上述分析可以发现规则波情况下沿岸方向的污染物输移速度基本在时均沿岸速度最大值的33%左右，该估计值可以在实际应用中作为参考，如果能够建立时均沿岸流与沿岸方向物质输移速度的关系，对于近岸污染物预报、保护、排污设施选址等都有积极的意义。

3.3 垂直岸线方向扩散系数的确定

对于由波浪引起的扩散，由于沿岸流速沿水深不是均匀分布的，存在离散现象，即沿岸扩散系数中包括离散系数，故分析难度比较大。但本文研究的是浅水问题(这时水平速度沿水深近似均匀分布)，垂直岸线方向离散作用较小，所以可以忽略波浪破碎引起的离散。

沿岸流垂直岸线方向扩散系数的确定一直是一个难题。本文通过假设垂直岸线方向的墨水扩散为一个高斯扩散过程，参考Satoshi等[10]分析得到的扩散系数估计值定义(式(6))，将污染物在一定浓度下通过高斯分布拟合得到的σxa(t)与本文得到的污染团离散程度数据比较，结果如图10所示。

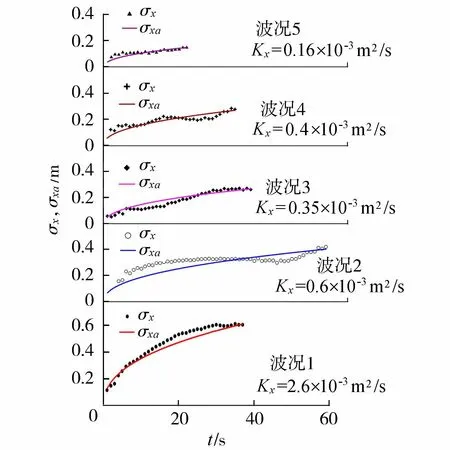
图10 波况1～5垂直岸线方向扩散系数的估计(C/C0=0.05)Fig.10 Estimation of diffusion coefficients in the cross-shore direction for Case 1 to Case 5 (C/C0 =0.05)

(6)

式中：σxa(t)——垂直岸线方向利用高斯分布拟合得到的离散程度；Kx——垂直岸线方向的扩散系数估计值；C0——污染物初始浓度；C——某一时刻污染物浓度。

污染团边界浓度C在输移过程中与初始值浓度C0的比值不断降低，图10给定的浓度比C/C0=0.05,该浓度对应的Kx变化最符合试验结果[20]。通过高斯扩散分布拟合5种波况的标准偏差得到σxa(t)，从而计算得到波况1～5垂直岸线方向的扩散系数估计值分别为2.6×10-3m2/s、0.6×10-3m2/s、0.35×10-3m2/s、0.4×10-3m2/s及0.16×10-3m2/s。由波况2与波况4、波况3与波况5可以看出，在波高接近情况下，周期由1.5 s变为2 s，对应的扩散系数则都相应减小，该结果同Bowen等[21]提出Kx∝HbYb/T(其中，Hb为该点水深，Yb为破波带宽度)中的扩散系数与波周期成反比相一致。

Satoshi等[10]在日本Hasaki海岸沿岸流场中进行污染物扩散试验，得到浓度分别为0.1%、0.5%、1.0%时，对应的垂直岸线方向的扩散系数Kx依次为0.01 m2/s、0.017 m2/s、0.025 m2/s。本文得到的扩散系数要比现场试验结果小1～2个量级，出现这种差异是有一定必然性的。这是因为，一方面二者空间尺度与水体掺混强度存在较大差异；另一方面野外非规则波与室内规则波的动力差异及近岸流场的易变性也明显不同，如现场试验中污染物扩散要受不平整地形的约束及海岸风应力的影响等，且现场近岸区域入射波都是多向不规则波(本文为单向规则波入射)。本文考虑将模型试验数据按照弗劳德相似准则换算成原型后进行量值比较分析。试验模型采用波高为3～5 cm，而实际工程中入射波波高为3～5 m，比例关系约为1∶100，考虑到试验模型的比尺效应，将扩散系数按比尺放大后各波况的结果为0.26 m2/s、0.06 m2/s、0.035 m2/s、0.04 m2/s及0.016 m2/s，与Satoshi等[10]现场试验的结果基本在同一量级范围内，故将本文试验结果进行比尺放大后可对实际工程中近岸污染物的监测及预报进行相应的研究指导。

4 结 论

a. 破波带内波流同时存在，由于沿岸流的作用，破波带内污染物主要在沿岸方向扩散。沿岸方向对流作用是水体表面污染物扩散的主要动力因素，规则波斜向入射情况下，沿岸方向的污染物输移速度约为时均沿岸速度最大值的33%。

b. 通过对污染团形心点坐标及离散程度的时空变化进行拟合，得到破波带内垂直岸线方向输移速度在0.008～0.03 m/s范围内，相对应的垂直岸线方向的扩散系数在0.16×10-3～2.6×10-3m2/s范围内。

c. 本文研究得到的结果比现场试验结果小1～2个量级，考虑物理模型的比尺效应，将试验模型波况要素数据换算成原型后进行量值比较，得到的结果与在日本Hasaki海岸的沿岸流场中的污染物扩散试验结果基本在同一量级范围内，故可将本文试验结果作为实际工程中近岸污染物监测、预报及控制等方面的研究参考。