基于动态网络流理论的扇区通行能力优化模型*

王莉莉，桂宝钧

（中国民航大学空中交通管理学院，天津 300300）

0 引言

空域对于民航运行是不可或缺的一部分，扇区作为空域的重要组成部分，其通行能力的高低直接决定了民航运行的效率。当扇区内部分关键航段和航路交叉点的流量达到一定数量时，一旦扇区内出现危险天气、军方活动、管制员工作失误等突发情况，将对扇区内航空器的运行产生巨大影响。因此，对扇区内航段的容量进行分析，构建一个合理的模型和算法，快速将流量分配到各航段上，对于提高空域资源的利用率、均衡管制员工作负荷、保障飞行安全具有重要的研究意义。

普遍状况下，扇区的通行能力可以理解为在空域限制、危险天气、管制员负荷、设施设备等因素影响下，单位时间内通过的最大航空器数量。在不同因素影响下，扇区通行能力会有一定的变化。扇区通行能力与扇区容量两者的概念有所区别：扇区容量是指单位时间内扇区所能提供服务的最大航空器架次，扇区通行能力一般小于扇区容量，当扇区的交通流量达到一定数量时，则航空器之间可能会出现拥挤，从而导致安全隐患。叶志坚等［1］提出了高空空域扇区调整和航路调整系统联合优化调整逻辑模型，发现航路网改造和重构空域扇区联合优化可大幅降低航班延误；王莉莉等［2］构建了航路与交叉点的阻抗函数，通过改进的Dial 算法对以航行时间最小为目标的模型求解，优化了终端区通行能力；Huang S 等［3］提出了交叉点飞机流量的紧凑配置，讨论了各种突发事件对于航路和扇区容量的影响，有效解决了飞机间的冲突；余静等［4］考虑了空域活动、航路长度及恶劣天气等因素的影响，改进了经典航路容量模型；田勇等［5］在结合扇区结构、民航规章、管制员工作负荷，以及机载气象雷达等信息的基础上，建立扇区动态容量评估模型并对其容量进行评估；胡勇［6］考虑管制员负荷与航线网运行等因素，提出了扇区通行能力仿真评估方法，并分析了交通流对通行能力的影响；D.Sun［7］等建立了多品种流的空中交通网络模型，解决了小时内的空中交通流量的分配；王晓晨等［8］基于输入航路对航段容量的影响，提出了随机因素多航段航路的容量方法；张兆宁等［9］考虑了军事活动影响，并对航路容量模型进行了改进得出航路容量评估模型；Milan Janic［10］基于管制员负荷建立了一种可确定最终容量的模型，预测了扇区未来时段内的交通流量；王世锦等［11］研究了不同构型节点的通行能力，并提出了提高节点通行能力的方法；贾铧霏等［12］从飞行受限区角度出发，建立了扇区动态容量影响模型并进行研究。

综上所述，对于管制扇区内航路的空中交通流分配的研究，以及为管制员提供可参考的分配流量模型还较少。针对上述问题，建立了一个多起讫点的扇区内航路交通流分配模型，设计关于扇区内航路的阻抗函数，在考虑航路容量、扇区内交通流随时间动态变化的特点、管制员负荷、危险天气和军方活动等因素的基础上，改进了最小费用最大流模型，通过实例验证，能够在受扰状况下合理且有效分配流量，提高扇区的通行能力。

1 管制扇区模型

1.1 扇区航路路径选择

为衡量航空器在扇区航路网络内飞行的连通性，同时体现流量分配的具体径路，引入一个决策变量δrs，若t 时刻交通流frs经过航路i-j 则取1，反之取0。设集合A 表示空中交通流在扇区内经过的航路，则可表示为：

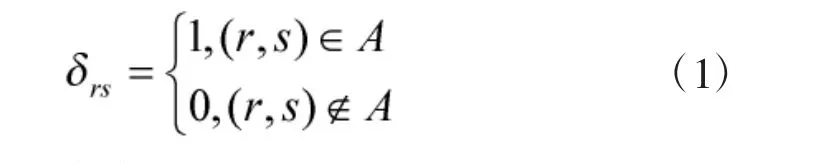
1.2 扇区内航路容量分析

根据现有研究成果，如下为航路理论容量模型：

其中，C 为航路最大容量，N 为服务的航空器总架次，T 为服务总时间［13］。

设v 为航空器在扇区内的航路上飞行平均速度，D 为标准管制间隔，ΔD 为管制员负荷、危险天气和军方活动等影响因素所增加的管制间隔裕度，则航空器经过航路所需时间T 为：

结合上式和航路容量定义式，单条航路的最大容量如下：

通过上式看出，航路最大容量模型兼顾了航路容量、管制设备精度和管制安全间隔等影响，但未考虑航路长度对容量的影响。

图1 航路AB 示意图

原有模型在计算航路AB（如图1 所示）容量时，未考虑在t 时刻航路上原有的航空器数量，仅认为是T 时段内进入航路AB 的飞机流。由此，将CT定义为以t 时刻开始的T 时段内从A 点进入航路AB 的飞机架次，称为航路起始点A 的过点容量；将CL定义为航路AB 的固定容量，航空器间均满足最低安全间隔要求。由此可得CT的求解公式：

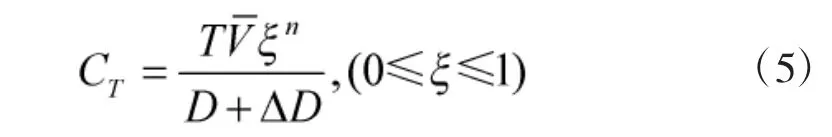
衡量到扇区内航段的端点一般为航路交叉点，故本文认为航段起点的容量与其连接航段数量有关，定义了扇区内航路交叉点复杂性的概念，用ξn表示：其中，n 为航路起点或扇区内航路交叉点所连接的航路条数，ξ 为介于0 和1 之间的常数，由实验数据测得，本文取ξ=0.95。

根据CL的定义可得：

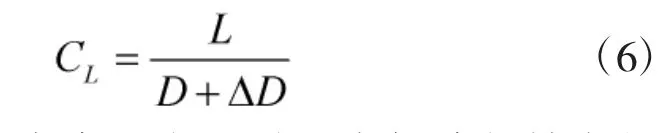
故航路的最大容量由T 时段内航路起始点的过点容量和航路固定容量两部分之和构成，公式如下：

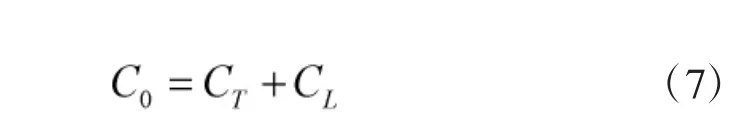
结合上式，得到航路最大容量模型：

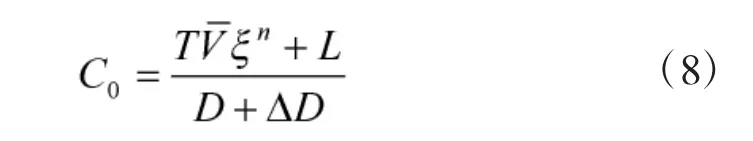
在计算扇区内航路动态通行能力时，采用如下思想：在航路最大容量模型的基础上，分析并确定管制员负荷、危险天气和军方活动的不同影响系数，取最小系数和航路最大容量相乘得到扇区内航路AB 的最大通行能力：

1.3 航段阻抗tm

对于非拥挤的扇区来讲，通常将航空器的航行时间费用视为常数，但对于各种因素影响下的拥挤扇区，此时时间费用随扇区内交通流量增大而增大。而其中被认为与流量分配最密切的因素是航行时间、通过流量、航段容量和阻塞系数。故定义阻抗函数为：

其中，tm代表航段m 上的阻抗，t0代表零流阻抗，即航空器在航段m 上自由飞行的时间，qm为航段m上的流量，Cm为航段m 在单位时间内的最大交通容量，即单位时间内最大航空器数量，α、β 为阻滞系数，由交通流分配程序测得，本文取α=0.15、β=1。

1.4 目标函数

扇区交通流量管理的目标是使扇区内的航空器总航行费用最小［14］，故可将目标函数设置为：

目标为求扇区内各航线费用之和最小，也即通过扇区网络的航空器的总航行时间最小。

1.5 约束条件

1.5.1 流量守恒约束

扇区应满足流量守恒约束。即在各时段t 各航段的流量xrs（t）之和等于扇区内航段总流量qrs（t）：

2 算法设计

传统的Ford-Fulkson 配流算法一次性将流量进行分配，而前文所提的航段阻抗是随流量变化的函数，因此，可将待分配流量分次加载到扇区内的航段上，这样将首份流量分配到扇区内航段网络后，航段阻抗也随之变化，时间费用自然也是最小的。故本文考虑了上述因素后，设计了一种考虑阻抗随流量变化的阶段性求解算法，模型如下：

步骤1 初始化。令各航段流量为零，以小时为单位进行交通流分配，得到各航段流量xrs（t）；令迭代次数N=1；

步骤2 更新各航段阻抗；

3 实例验证

3.1 实验设计

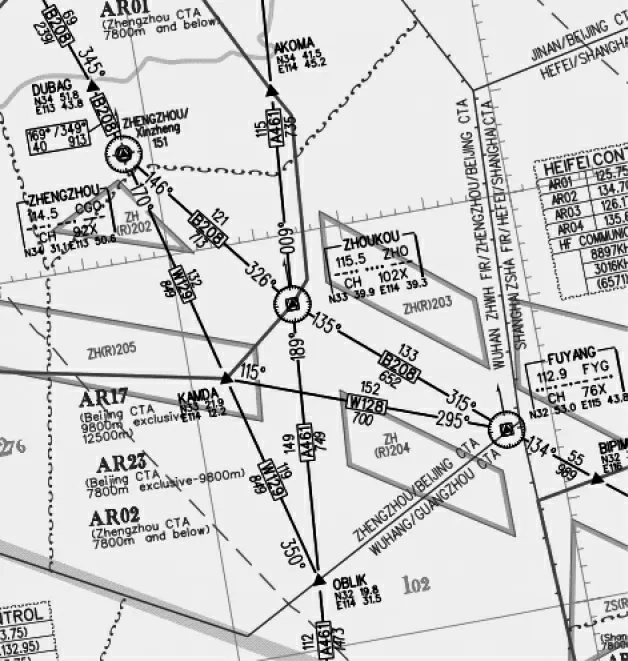
图2 北京17 号区域管制扇区

本文选取了周口所在北京17 号区域管制扇区，如图2 所示（AIP），部分航路段由于NAIP 涉密未显示完全，本文遵循实际的航路段情况。该扇区是一个多起讫点的构型，故添加虚拟节点使其化为单起讫点问题，并设连接虚拟节点的虚拟航段的容量为M（任意无穷大数），图3 虚线所连接的圆S 为虚拟进入扇区节点，t 为虚拟出扇区节点。

3.2 容差分析

网络节点的容差ΦA是指以A 为始点的航段容量总和与所有以A 为终点的航段容量总和之差，从网络结构上标志在该节点发生阻塞的可能性，当ΦA≤0 时说明该点从结构上发生阻塞。对扇区内各航路交叉点的容差进行计算，发现只有6 号周口节点的容差ΦZHO≤0，则该点在结构上可能发生阻塞。故视周口节点为扇区内最为关键的节点，考虑其与扇区进出点直接相连的关键航段进行流量分配，图3 中加粗实线为关键航段。

图3 北京17 号扇区抽象图表示

3.3 航段信息

依据航路运行实际情况和相关规定，航空器之间的标准管制间隔D 取30 km，管制间隔裕度ΔD取5 km，航空器平均速度v 取800 km/h。不同因素对航路最大容量的影响系数不尽相同：设天气状况的影响系数αTi=0.95、军方活动的影响系数βTj=0.9、人为因素的影响系数γTk=0.8。航段信息如下页表1所示。

3.4 仿真结果

对实验设计的算例进行仿真分析，工具为MATLAB 2017a。根据本文所设计的阶段性求解的近似算法，对将通过扇区的空中交通流量进行分配，待分配的航空器架次分别为24 架、35 架、44架、60 架，模拟在1 h 内的不同流量情况，当待分配的流量大于等于44 架/h，每条航段的流量和扇区内流量不再增加，以此得出各航段和扇区的最大流量，此时总流量为44 架/h，结果如表2 所示，此时扇区内主要航段容量-流量比如图4 所示。

由仿真结果可知，本文所建立的模型可以在受阻情况下有效优化扇区内交通流量的分配，使各航段的流量得以合理分配，接近扇区内各主要航段的最大通行能力。

4 结论

本文建立了航路的最大通行能力模型，随后基于动态网络流理论，对区域管制扇区的通行能力进行了模型建立、优化和改进。以北京17 扇区为例，仿真了在管制员负荷、危险天气和军方活动等因素影响下的流量分配过程。

表1 航段信息

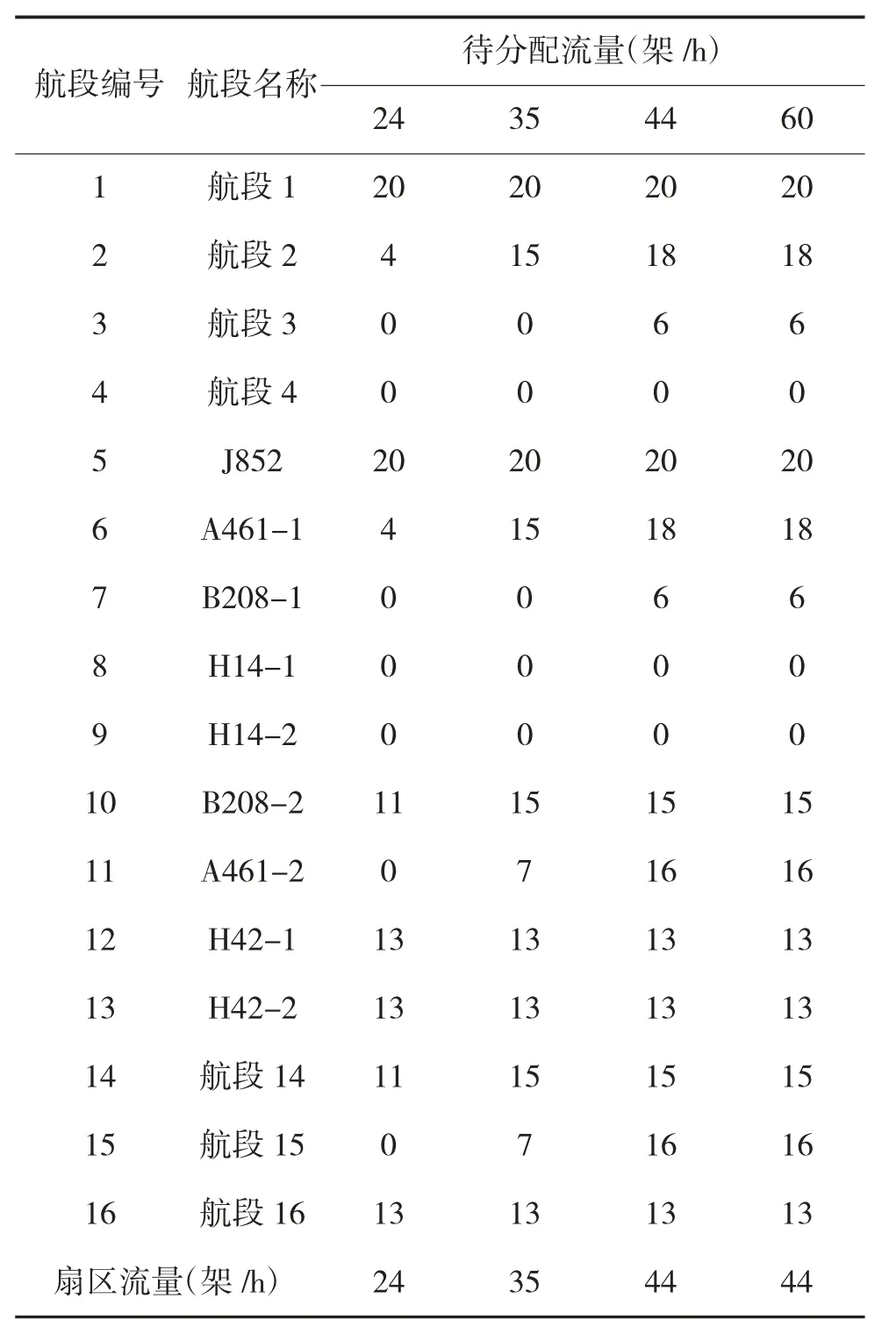
表2 阶段性求解的近似算法结果

图4 扇区内主要航段容量-流量比图

建模方面，基于现有的航路理论容量模型研究成果，考虑了航路长度对航路容量的影响，并找出影响容量的因素，以此建立扇区内航路的最大通行能力模型。衡量扇区内交通流量随时间动态变化，提出了航段阻抗函数，建立了考虑网络流量的航段容量和动态变化的最优化模型。

求解方面，提出了一种阶段性求解的近似算法，能快速地把空中交通流分配到扇区内的航段上。

仿真结果表明，本文所设计的模型和算法能够将待通过扇区的流量快速地分配到各航段。本文的模型可进一步改造为考虑高度层变化的进近扇区流量分配模型，从而为管制员在更多情景下的流量分配提供决策依据。