基于扩张观测器火箭炮伺服系统鲁棒控制*

吴跃飞，殷晓晴，崔林威

（南京邮电大学自动化学院，南京 210023）

0 引言

多管防空火箭炮伺服系统负载非线性摩擦对系统的动态及静态性能影响很大，而系统中存在的不平衡力矩大范围变化及方位框架和俯仰框架之间不可避免的耦合干扰作用等，使得系统存在严重的非线性［1］。针对火箭炮伺服系统在不确定干扰下的控制问题，通常采用的方法是采用基于干扰观测器（Disturbance Observer-Based，DOB）的方法。这种方法能够有效地抑制各种干扰，并能减弱非线性对系统的影响［3］。而在实际的应用中，速度和压力信号难以测量，信号中的噪声往往比较大，导致测量信号不能直接用于实际系统中［2］，并且由于反馈定律的微分运算，最终控制输入是不连续的，这可能导致跟踪性能下降。为了避免抖动问题，在机器人控制中应用了一种新的误差符号鲁棒积分（RISE）输出控制方法，以补偿有界不确定性和干扰［3］。RISE 方法的关键特征是可以通过使用误差反馈项符号的连续鲁棒积分来适应有界干扰。该控制方法利用RISE 反馈项来适应不匹配建模不确定性，并且合成自适应律以处理匹配的参数不确定性，已成功应用于机械手［4-5］和液压执行器［6］。

基于以上分析，本文将基于扩张观测器的积分鲁棒控制方法（RAISE）应用于火箭炮转塔伺服系统，同时考虑系统实际运行时高频噪声和转塔耦合干扰问题，采用扩张状态观测器，实时补偿系统干扰。同时，积分鲁棒控制方法（RISE）也可以有效地解决建模不确定性的问题，而且可以获得连续的控制输入和渐近跟踪的性能［5-7］。

1 问题描述及数学模型

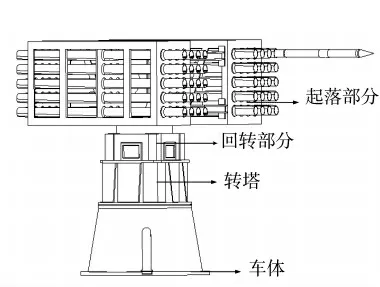
图1 火箭炮转塔伺服系统示意图

由图1 可知，俯仰子系统的起落部分相对于回转部分的俯仰运动，定义θl为炮塔相对车体的实际高低转角。本文研究对象为其俯仰子系统，执行机构为交流永磁同步电机（PMSM），通过减速器带动负载发射箱转动，则系统的数学模型表示为［6］：

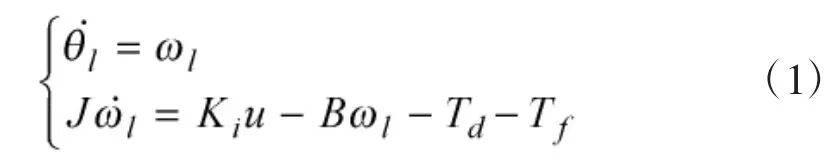
式中，J 为发射架负载转动惯量与电机折算至负载端等效转动惯量之和；Ki为电机转矩系数；B 为等效阻尼系数；Td为耦合干扰力矩。Tf是负载摩擦扭矩，可以把负载受到的摩擦力矩表示为：

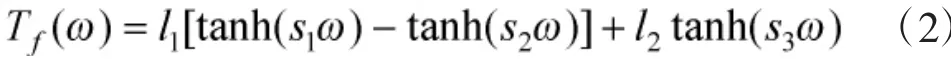
此静态模型关于速度的曲线特性如图2 所示。取参数l1=150，l2=30，s1=200，s2=160，s3=200。

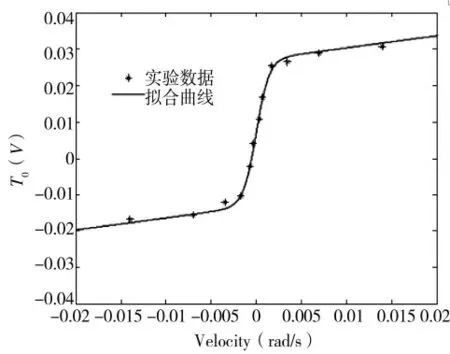
图2 摩擦静态模型关于速度的拟合曲线

令x1=θl，x2=ωl，定义状态变量x =［x1，x2］T，由式（1）、式（2）所述，则动力学方程转化为

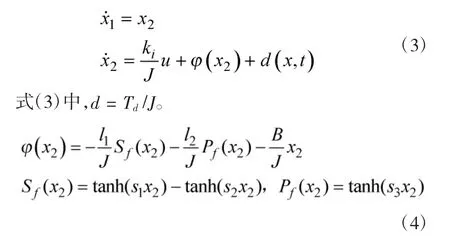
2 控制器设计

2.1 扩张状态观测器的设计

2.2 反步控制器的设计

3 稳定性证明

4 仿真结果及分析

火箭炮伺服系统主要参数如下［2］：满载惯量折算为J=0.002 627 kg·m2，B=0.000 143 N·m·s，Ki=1.11 N·m/A，N=1∶231，不平衡力矩和摩擦力矩折算为4.86 N·m。

系统跟踪信号x1d（t）=0.2sinπt·［1-exp（-0.01t3）］rad。选取以下3 种控制器进行仿真验证：

1）误差符号积分鲁棒控制器（RAISE）：取控制器参数k1=250，k2=20，kr=2，β=2，自适应增益Г=diag{100，50，50，50}。

2）误差符号积分控制器（RISE）：即所设计的RISE 控制器中不含扩张观测器部分。为保证对比公平性，其控制器参数与RISE 控制器中对应的参数相同。

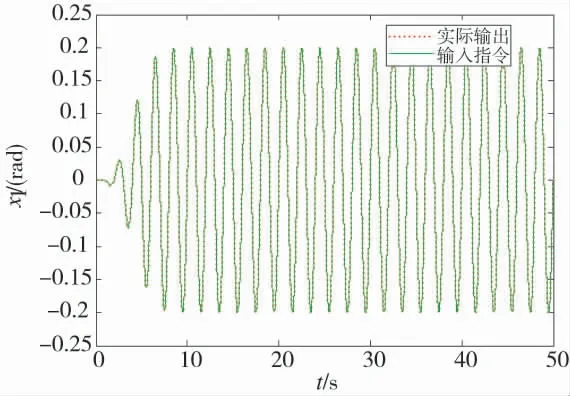
图3 RAISE 控制下系统实际输出曲线

RAISE 控制下系统的跟踪性能曲线、两种控制器作用下的跟踪误差曲线分别如图3、图4 所示。由图4 可知，所设计的RAISE 控制器的跟踪性能都要优于相对比的RISE 控制器和RISE 控制器。

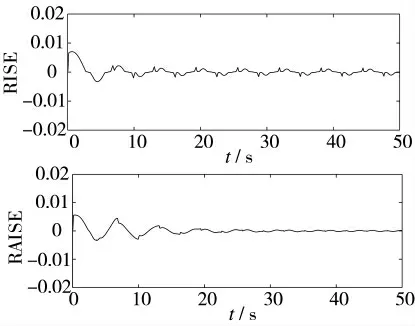
图4 系统的跟踪误差曲线

仿真条件1：0 s 时刻给定阶跃信号θref=15°，1 s时刻在电机轴上每间隔0.2 s 加载幅值为15 N·m，持续时间为0.01 s 的脉冲力矩来模拟火箭炮发射时的冲击载荷。系统阶跃响应、控制输入如图5、图6所示：

图5 带扰动的阶跃响应曲线

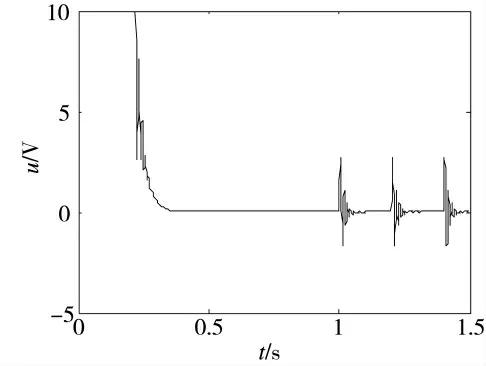
图6 控制输入

仿真条件2：给定正弦信号θref=15°sin（0.5πt），从第0 s 开始至10 s 过程中，均匀增加至4 倍转动惯量直至结束，系统的跟踪误差曲线以及控制输入如图7、图8 所示：

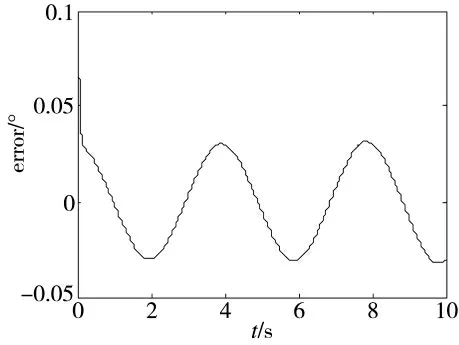
图7 跟踪误差曲线

图5 和图6 表明，采用该控制策略时系统鲁棒性较强，对模拟的燃气流冲击力矩的扰动不敏感，且控制输入量相对平滑。图7 和图8 表明，火箭炮系统在进行轨迹跟踪时动态精度较高，控制输入量平滑［8-9］，同时系统对于转动惯量变化不敏感。

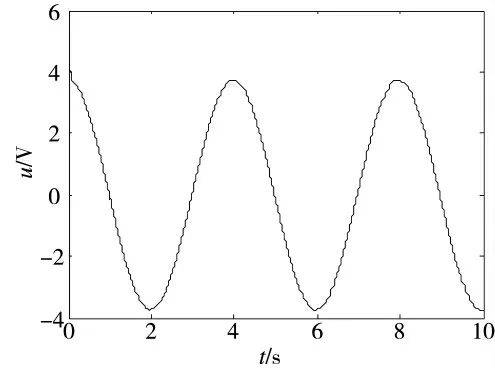
图8 控制输入

5 结论

本文针对具有不可测状态和未知外界干扰力的火箭炮转塔控制系统问题，将包含未知外负载力的干扰项视为未知输入，构造未知输入观测器，然后基于扩张观测器设计鲁棒输出反馈控制器，通过所提出的鲁棒积分控制器，获得了良好的比较仿真结果，以验证所提出的控制策略的有效性，实现了在存在参数不确定性和各种干扰的情况下的渐近跟踪性能。