基于CE-CAPSO 武器目标分配优化算法

王力超，乔勇军，李永胜

（1.海军航空大学，山东 烟台 264001；2.解放军31004 部队，北京 100089）

0 引言

武器目标分配（WTA）是指在一定约束条件下（如武器种类和数量受限），按照武器毁伤概率、弹药成本、目标威胁程度、作战任务要求等条件将武器与目标匹配、分配，以达成作战目标最佳效果的过程，是典型的非线性组合优化问题［1］。其中模型求解的关键是计算的精度和速度。

当前，求解WTA 问题主要采用启发式算法，如遗传算法、蚁群算法、模拟退火算法等。粒子群（PSO）算法由于其参数简单，易于实现且收敛速度快的优点，得到了广泛的应用。PSO 源于对鸟群捕食行为的模拟，是一种随机搜索的迭代进化算法。但PSO 算法存在容易陷入局部最优，从而导致“早熟”的问题，为此，研究人员通过分析算法的原理，提出了很多改进方法。文献［2］提出了一种云自适应粒子群算法（CAPSO），文献［3］提出了一种基于鲶鱼效应的粒子群算法（CEPSO），这些优化均取得了满意的结果，在一定范围内改善了算法的性能。

为了加快粒子寻优和避免陷入局部最优，在基本粒子群算法的基础上，受文献［3-4］的启发，提出一种求解WTA 问题的改进云粒子群算法——CE-CAPSO 算法，仿真实验结果表明，本算法具有更好的全局寻优能力，收敛速度也有明显提高。

1 WTA 问题模型

其中，第1 个不等式表示第i 种武器平台打击所有目标使用武器弹药不超过自身拥有的数量mi；第2个约束条件表示消耗的武器弹药是非负的。

由于作战资源有限或目标威胁度不高，实际战场环境下，不一定攻击或拦截所有目标，通常指挥员会根据实际情况权衡各种因素，确定一部分目标必须打击，而其他目标“可打可不打”，因此，在这里假设前t 个目标必须要受到打击，所以约束条件变为：

2 基于PSO 武器目标分配算法

2.1 基本粒子群算法

在PSO 算法中，粒子在d 维空间中的位置（x）和飞行速度（v）都表示为一个矢量，每次迭代都有一个标准评价粒子的位置的好坏，称之为适应值函数（fitness function），此外粒子们知道自己到目前为止最好的位置（pbest）和整个粒子群中历史上最好的位置（gbest），前者称之为个体认知经验，后者为社会认知经验，粒子通过个体认知经验和社会认知经验经过一定次数迭代寻找d 维空间中最好的位置［6］，其速度与位置更新公式如下：

2.2 粒子编码方式

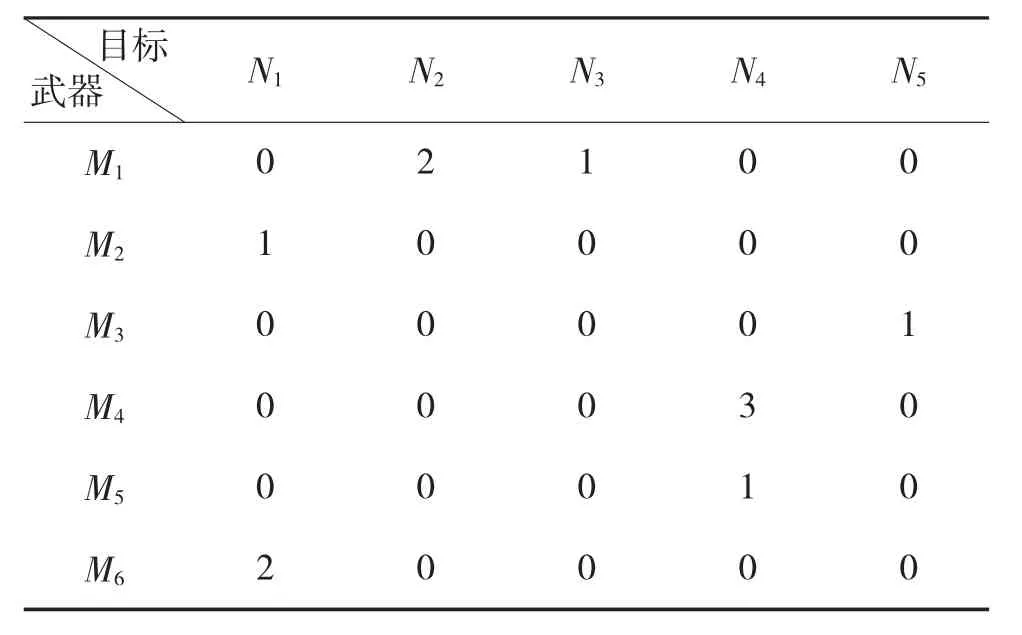
表1 例子编码方式示意

表格中数字表示该单元格行武器打击该单元格列目标所消耗弹药数量，如M4武器平台打击N4消耗3 枚弹；0 为不打击。矩阵编码的方式，减少了计算循环次数，降低了计算步骤复杂度。

2.3 约束条件处理

WTA 是多约束问题，直接计算效率不高，因此，在这里利用罚函数方法，把约束条件合并到适应值函数中，引入惩罚因子W，惩罚因子通常为一个较大的数；另外，为了计算方便，改写目标函数为倒数形式，求最小值，改写后的适应值函数如下：

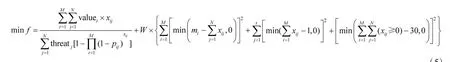
式中，第2 项大括号中3 项分别表示对武器弹药消耗的约束、对打击到前t 个目标上武器弹药的约束和对武器弹药非负的约束，（xij≥0）表示逻辑运算，xij大于等于0 为真，取值1，否则为假，取值0。

3 改进的粒子群算法

虽然粒子群算法简单易于实现，但有早熟收敛、易于陷入局部最优和后期粒子多样性差的问题，解的精度和迭代速度达不到要求的标准，因此，在基本粒子群算法的基础上，引进云自适应模型与鲶鱼效应模型，来改进粒子群算法的不足。

3.1 云自适应粒子群算法

粒子群算法中惯性权重决定粒子飞行速度，传统对于w 参数改进有线性递减、自适应权重法，在迭代初期w 值较大，利于粒子全局寻优，后期w 较小，利于粒子较快收敛，这在一定程度上提升了算法性能，但却造成了后期粒子易于陷入局部最优而找不到全局最优解的尴尬。李德毅院士提出了云理论，使用随机正态分布的云模型既具有稳定倾向性又有一定随机性、模糊性，而且对于很多不确定模糊问题，用正态隶属描述最合适，可以达到很好的效果，云模型用期望Ex、熵En、超熵He 和正态随机数En'描述［8］，给定期望、熵、超熵以及云滴数，就可以通过“云发生器”计算得到云滴定量值和相对该模糊问题的确定度。云自适应粒子群算法（Cloud Adaptive Particle Swarm Optimization Algorithm，CAPSO）［4］根据粒子适应度将粒子分为3 个种群，并把不同惯性权重用于不同种群粒子迭代中。基本内容是：根据适应值函数求出粒子群平均适应值favg，将适应值优于favg的粒子求平均得到favgnice，将适应值次于favg的粒子求平均得到favgbad，惯性权重w 的取值规则如下：

1）优于favgnice，此时粒子的位置已非常接近全局最优解，因此，w 取0.4 加快粒子收敛速度；

2）次于favgnice但优于favgbad，这是质量一般的粒子，采用云自适应模型非线性调整惯性权重：

3）次于favgbad，此时粒子较差，w 取0.9 加快粒子飞行速度以寻找全局最优解。

加入云模型提高了粒子寻优能力和收敛速度，但是算法运行后期粒子还会有陷入局部最优的风险，因此，引入鲶鱼效用模型，加入扰动，使得在算法运行后期陷入局优的粒子重新获得活力。

3.2 鲶鱼效应——云自适应粒子群算法

鲶鱼效应（Catfish Effect）是指在沙丁鱼群中放入几条鲶鱼，生性安逸的沙丁鱼看到好动的鲶鱼紧张起来而四处游动，从而保持沙丁鱼活跃。在粒子群迭代过程中，粒子后期易于陷入局部最优解而导致算法准确度不高，因此，借鉴鲶鱼效应，标记不同粒子为鲶鱼粒子和沙丁鱼粒子，使得适应值较差的粒子加速运动寻优，增加粒子群的多样性［3］。方法如下：

1）每次迭代判断粒子当前位置与历史最好位置，如果相同，则标记此粒子为鲶鱼粒子，否则为沙丁鱼粒子cei=0，鲶鱼粒子表示粒子陷入了局部最优，标记为沙丁鱼的粒子要远离鲶鱼粒子；

2）定义沙丁鱼粒子逃逸速度［9］为：

3.3 改进CE-CAPSO 粒子群算法

粒子速度更新由惯性项、个体经验项和社会经验项构成，CAPSO 将粒子群按适应值不同分为3 个种群：较好种群、一般种群和较差种群，分别采用不同惯性权重来计算。借鉴文献［12］思想，改进粒子速度更新公式：对于较好种群，其适应值已经接近全局最优解，因此，速度更新采用社会经验模型，加快全局收敛；对于较差种群，采用个体经验模型；而对于一般种群不作改动，因此，修改后粒子速度更新公式如下：

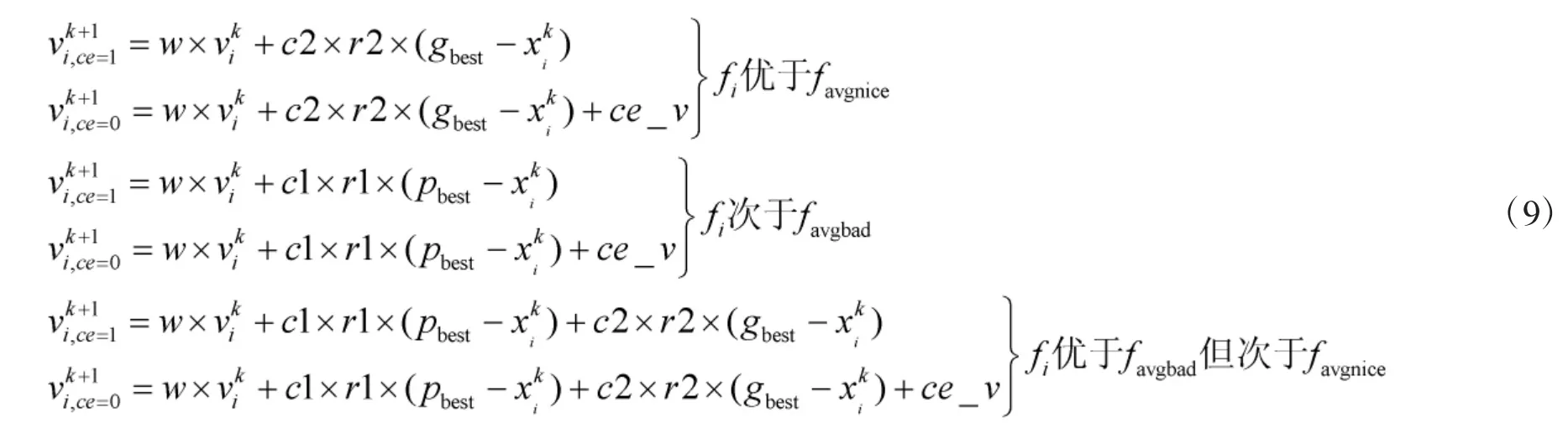
4 仿真实例

4.1 参数设置

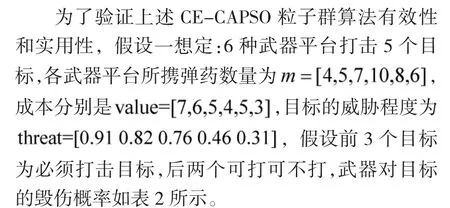
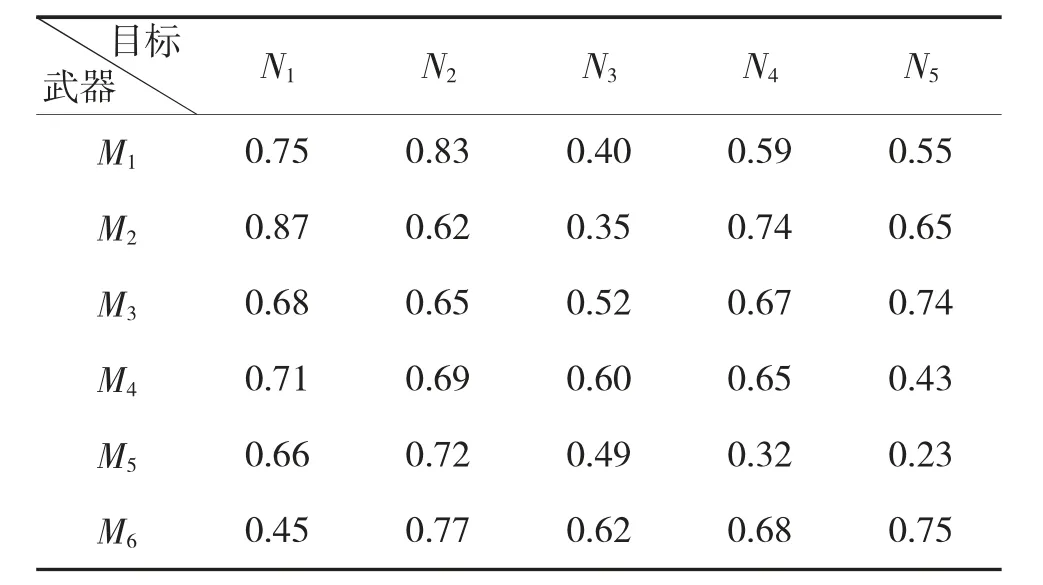
表2 武器毁伤概率

分别通过基本粒子群算法（PSO）、云自适应粒子群算法（CAPSO）、鲶鱼效应-云自适应粒子群算法（CE-CAPSO）、改进CE-CAPSO 算法，与基于轮盘赌选择的自适应交叉变异遗传算法（GA）的仿真分析对比。PSO 惯性权重w 设为0.5，三者学习因子都为2，在CE-CAPSO 中，根据正态函数规则，En 越大，云滴覆盖宽度越大，结合算法速度和精度，将α=2.9，He 决定云滴的随机性，取β=10［4］，n 决定沙丁鱼粒子逃逸速度，根据经验，取n=2。GA 算法设置两种，GA1 最小交叉概率0.3，最大交叉概率0.6，最小变异概率0.02，最大变异概率0.05；GA2 最小交叉概率0.3，最大交叉概率0.8，最小变异概率0.03，最大变异概率0.06，轮盘赌最大选择概率0.2，第j个个体的选择概率是：

GA 个体与PSO 粒子编码方式略有不同，即把后者的矩阵改写为一维数组形式，方便个体遗传时交叉和变异操作，其形式如图1 所示。

图1 遗传个体编码示意

遗传操作的自适应交叉概率Pc和变异概率Pm计算公式如下：

4.2 结果分析

利用Matlab R2017b 编写程序，设置粒子种群数量popsize=50，迭代次数gen=80，运行计算结果如下页图2～图7 所示。

图2 PSO 计算结果

图3 CAPSO 计算结果

图4 CE-CAPSO 计算结果

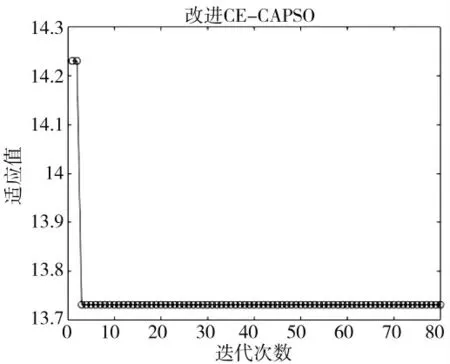
图5 改进CE-CAPSO 计算结果

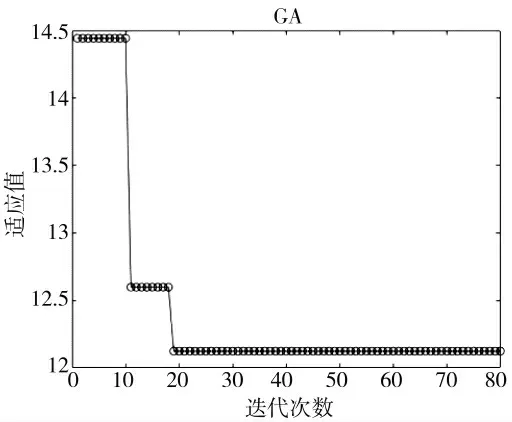
图6 GA1 计算结果

图7 GA2 计算结果

从图中对比可以发现，相比于PSO、CAPSO、GA算法，文中提出的CE-CAPSO 算法与改进的CE-CAPSO 迭代速度最快，GA2 次之，然后是GA1 和CAPSO，PSO 最差。在上述参数设置下，CE-CAPSO与改进的CE-CAPSO 基本上在10 代左右就收敛到最优解，而CAPSO、PSO 和GA 算法迭代次数均大于10 代；另外4 种算法的适应值依图片排序分别为13.729 3、13.893 8、14.830 4、14.816 1、12.121 3、17.101 6， 呈GA2>CE-CAPSO> 改 进CE-CAPSO>CAPSO>PSO>GA1 状态，但是适应值的大小并不能完全说明GA2、CE-CAPSO 的寻优能力差，而PSO、GA1 的寻优能力最好，因为WTA 问题属于离散问题，适应值最佳并不代表算法求得武器目标分配方案最好，还可能不符合约束条件或者现实情况，而且给定的参数也可能造成解不唯一；此外PSO、GA 本质上都是随机搜索算法，且文中处理约束条件的方法是罚函数法，沙丁鱼粒子逃逸速度也是固定值，没有考虑其与鲶鱼粒子的相对距离，而GA 算法受参数影响较大，参数的不同会造成解相差也较大，计算结果有一定随机性且仍不可避免有较小的概率陷入局部最优。

运行多次分析这几个算法得到的结果，发现它们的计算结果并不每次符合所有约束条件；而对于GA 算法，不同的参数设置计算结果也有较大不同，5 种算法之间寻优能力各不相同。现将程序分别运行100 次，统计符合约束计算结果如下页表3 所示。

从表中可以看出，改进遗传算法准确性最佳，其次是改进CE-CAPSO、CE-CAPSO、CAPSO 算法，PSO 算法准确性最差；粒子群一类算法平均迭代次数与准确性呈相同趋势，其中引入云模型后，算法迭代次数显著减少，而遗传算法由于其本身容易早熟特性，收敛迭代次数较小；5 种算法中，粒子群一类算法迭代标准差相差不大，CAPSO 最稳定，而GA 算法的收敛迭代次数受参数设置较大；相比标准粒子群算法，改进的粒子群适应值较为稳定，最稳定的是CE-CAPSO 算法；但是适应值最佳的是CAPSO 算法，其次是PSO、CE-CAPSO 算法，而改进CE-CAPSO 算法适应值略差，而遗传算法过早收敛，容易陷入局部最优，解的质量不高；对比这几种算法的平均运行时间，都在同一个数量级且相差不大。

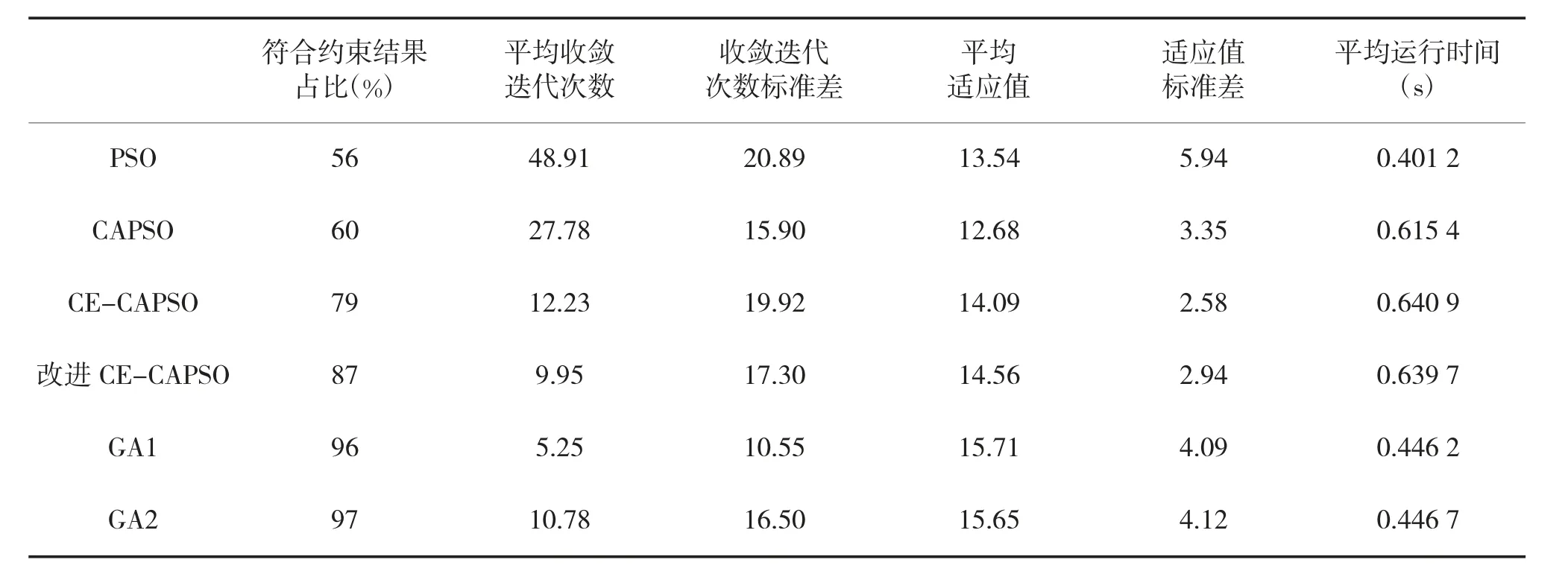
表3 4 种算法统计对比

5 结论

通过对基本粒子群算法改进，引入了云模型与鲶鱼效应，建立相应算法模型，计算并分析得到如下结论：基本粒子群算法迭代速度慢且求解正确性不高，基于CAPSO 算法加快了粒子全局寻优、收敛速度和正确性；在此基础上又引入鲶鱼效应，避免粒子迭代陷入局部最优，增加粒子群多样性。针对武器目标分配问题求解使用基于CE-CAPSO 算法大大提升了计算效率，同时提高了计算准确性。相比于GA 算法，粒子群实现简单，对计算机性能要求不高，可以有效求解WTA 问题模型，满足实际运用。综上，改进的CE-CAPSO 算法，在解的正确率、收敛速度和全局寻优方面都有一定提高，有较好的适用价值。

但是WTA 模型求解很大程度上依赖参数设置，而作战实际情况多样，符合要求的往往有多个合法解，难以保证每次计算结果一致，只能在计算的效率和准确性上提升算法性能，此外，本文没有对学习因子、改进进行考虑，而二者决定粒子学习自身经验与种群经验的程度，因此，可以进一步地研究，对学习因子的改进进行有益的探索。