破片和冲击波复合作用下装甲板毁伤效应预测

李 峰，石 全，张 芳，胡 备，王 谦

（1.陆军工程大学石家庄校区，石家庄 050003；2.解放军32178 部队科技创新研究中心，北京 100012）

0 引言

预制破片式战斗部对装甲板毁伤效应研究中，其毁伤效应不仅是破片和冲击波对装甲板毁伤的简单叠加，而是有更加复杂的毁伤机理。吕勇［1］等人分析了不同时序下破片和冲击波复合作用对天线等效靶板的毁伤，表明破片和冲击波复合作用对天线靶板的毁伤不是两者简单叠加的结论［2］。陈长海［3-4］等人对破片和冲击波的耦合区间进行了研究，建立了破片和冲击波的耦合作用区间理论模型。蒋建伟和侯俊亮［5-6］等人研究了预制孔靶板在爆炸冲击波作用下的动态响应，分析不同孔径、孔数对冲击波毁伤效应的影响，建立了可以用于计算不同孔靶板的中心点挠度公式。目前复合毁伤效应研究已经取得许多成果［7-8］，但对破片和冲击波复合作用对装甲板的毁伤效应相似性的研究较少，刘锋［9］等人研究了破片对靶板的等效设计试验，通过量纲分析和数值模拟的方法，得到了破片对靶板的毁伤直径预测公式，利用该公式能够进行不同厚度、密度、剪切模量的靶板等效，不足之处是缺少复合作用下对毁伤直径的研究。

本文对破片和冲击波复合作用下装甲靶板的毁伤直径进行研究，通过量纲分析，建立破片和冲击波复合作用下靶板毁伤直径无量纲方程，采用数值模拟方法，建立破片和冲击波复合作用下的毁伤直径预测方程，利用该公式可以进行毁伤直径的预测。

1 量纲分析

1.1 破片和冲击波复合作用对装甲板毁伤效应的影响因素分析

破片和冲击波复合作用对装甲毁伤效应主要受破片、炸药、空气和装甲的影响，因此，装甲毁伤直径主要受到以下几个方面的影响：

1）破片相关参数：破片的直径d，破片的入射速度V，破片的入射角度α，破片的弹性模量Ep，破片的剪切模量Gp，破片的屈服强度σyp，破片的极限强度σsp，破片的密度ρp。

2）炸药相关参数：装药量Q，单位质量装药所释放化学能e，装药密度ρe，爆炸气体绝热指数γe，爆轰速度D。

3）空气相关参数：初始状态压力p0，空气密度ρa，空气绝热指数γa。忽略空气温度、传热性和空气粘性等次要因素。

4）装甲相关参数：靶板的厚度h1，靶板的弹性模量Et，靶板的剪切模量Gt，靶板的屈服强度Syt，靶板的极限强度Sst，靶板密度ρt，忽略靶板尺寸的影响。

5）距炸药几何中心距离H。

1.2 破片和冲击波复合作用对装甲板毁伤效应的量纲分析

采用MLT 系统，以质量M、长度L、时间T 作为基本量纲，各个物理量量纲如表1 所示。

因此，由相似第2 定理可知，装甲靶板的毁伤直径D1与以上因素的关系为：

取H，Q，D 为基本物理量，则式（1）转化为∏方程为：

表1 装甲板毁伤效应相关参数及其量纲

破片和冲击波复合作用对装甲毁伤过程中，在同一环境下使用相同材料的破片和同一种类的炸药对装甲进行毁伤时，毁伤直径影响因素中有16个因素与原型相一致，即：

2 有限元模型建立及材料参数选取

2.1 装甲板毁伤直径物理模型

破片在对装甲板毁伤过程中会在入射方向上对装甲表面产生一定距离的毁伤，这里称它为毁伤直径，在入射方向上破片和冲击波对装甲板毁伤直径如图1 所示。

图1 装甲板毁伤直径

2.2 有限元模型建立

本文主要研究破片先作用冲击波后作用的结果，因此，在破片作用完后再激活冲击波和炸药，故设置在0.1 ms 时激活空气域和炸药。考虑到模型的对称性，以y 轴为对称轴，建立1/2 模型，单位制为mm-mg-μs-k，炸药在距离装甲靶板50 mm 处起爆，起爆采用点起爆方式，设置在距离靶板50 mm 位置，冲击波和靶板之间作用采用流固耦合算法［10］，有限元模型如图2 所示。

2.3 材料参数选取

破片状态方程采用Shock，强度模型采用Johnson Cook，侵蚀模型采用Geometric Strain。装甲靶板材料选用4 340 钢，采用Shock 状态方程、Johnson Cook 强度方程、Johnson Cook 失效模型和Failure 侵蚀模型进行描述。炸药选用TNT［8］材料，采用JWL状态方程进行描述。空气域为理想气体状态方程［11］，γ 取 值 为1.4，密 度 为1.225 mg/cm3，e 取 值 为2.068×105。各个材料的参数引用文献［9］。

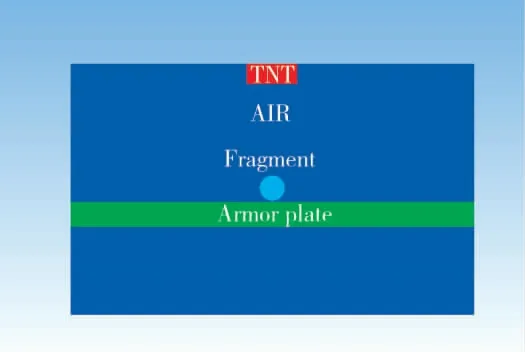
图2 有限元模型

3 装甲毁伤直径相似规律数值模拟

3.1 破片和冲击波复合作用对装甲板毁伤过程分析

通过破片和冲击波复合作用对装甲靶板毁伤的数值模拟，得到不同时刻破片和冲击波复合作用对装甲板毁伤云图和装甲板节点径向位移变化曲线。由图3 可知，整个毁伤分为两个部分，第一部分是破片对装甲板进行毁伤，第二部分是冲击波对装甲板进行毁伤。破片对装甲板进行毁伤时，在侵彻初期，主要是装甲板的毁伤形成过程。随着破片的侵彻深入，装甲板的毁伤逐渐增大，当破片完全侵彻进靶板时，装甲板毁伤几乎不变，随着侵彻的继续深入，破片穿透装甲板［11］。当TNT 起爆后，在起爆点周围产生了局部超压区域，冲击波向装甲板传播，在125 μs 时，冲击波到达装甲板，开始对装甲板进行毁伤，在毁伤区域产生了局部应力集中，使得装甲板毁伤区域进一步扩大，加剧了对装甲板的毁伤［12］。由图4 可以看出破片和冲击波复合作用时装甲板节点径向位移大于破片和冲击波单独作用时位移之和，与文献［1］的结论一致。

图3 不同时刻装甲毁伤云图

图4 装甲板节点径向位移曲线

3.2 装甲毁伤直径公式建立

进行不同破片直径、入射速度、入射角度、装甲板厚度条件下装甲板毁伤直径数值模拟。炸药尺寸为20 mm×16 mm×16 mm，中心距装甲板高度为50 mm。破片直径d 分别取值8 mm、9 mm、10 mm、11 mm、12 mm、13 mm，基准值为10 mm。破片入射速度V 分别取值为1 000 m/s、1 100 m/s、1 200 m/s、1 300 m/s、1 400 m/s、1 500 m/s，基准值为1 300 m/s。破片入射角度α 分别取值为0°、7.5°、15°、22.5°、30°，则对应90°-α 为90°、82.5°、75°、67.5°、60°，基准值为90°。装甲板厚度h1分别取值7 mm、8 mm、9 mm、10 mm、11 mm、12 mm，基准值为10 mm。不同量纲参数值条件下毁伤直径量纲值如表2～表5所示。

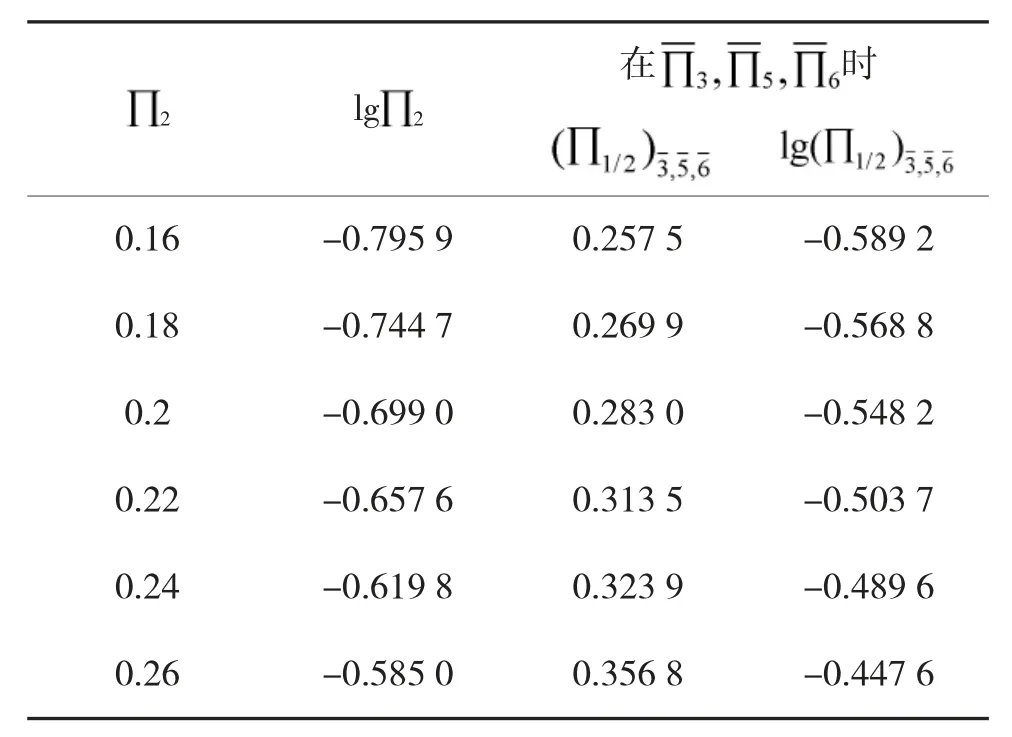
表2 破片直径变化时毁伤直径量纲值

表3 装甲板厚度变化时毁伤直径量纲值

表4 入射速度变化时毁伤直径量纲值

表5 入射角度变化时毁伤直径量纲值

表6 各量纲下的m 和b 值

式中，D1为毁伤直径（mm），α 为破片的入射角度，V为破片的入射速度（m/s），D 为爆轰速度（m/s），d 为破片的直径（mm），h1为装甲板厚度（mm），H 为炸药几何中心距装甲板表面距离（mm）。

根据破片的入射速度、入射角度、直径、炸药的爆轰速度、装甲板的厚度，以及炸药中心距装甲板表面距离，可以进行复合作用下装甲板毁伤直径的预测［13］。

进一步开展不同入射速度、入射角度的破片和冲击波复合作用，对装甲板毁伤的数值模拟计算。表7 为各工况下的毁伤直径预测值与仿真计算值。可以看出，在参数取值范围内进行试验，预测值与仿真计算值误差在5 %以内，通过量纲分析建立的毁伤直径预测方程是较精确的，因此，利用建立的毁伤直径方程，可以较好地预测装甲板在破片和冲击波复合作用下的毁伤直径，以评估装甲板受损情况［14-15］。

表7 各工况下的毁伤直径预测值与仿真值对比

4 结论

通过破片和冲击波复合作用对装甲板的毁伤效应相似性进行研究，采用量纲分析方法建立了毁伤直径与影响因素之间的无量纲方程；利用有限元软件AUTODYN 对破片和冲击波复合作用，对装甲板毁伤进行了数值模拟，得到了各个影响因素下的装甲板的毁伤直径，建立考虑破片入射速度、破片入射角度、破片直径、装甲板厚度的装甲板毁伤直径预测方程，并通过仿真对预测方程进行验证，将预测方程计算结果与仿真试验结果进行对比，误差在5 %以内，可以较好地预测装甲板的毁伤直径。