基于AHP- 熵值法的摩托化机动演训效果评估*
王 刚,周华任,刘炳男,王赫彬
(1.陆军工程大学基础部,南京 211101;2.陆军工程大学火炮工程系,石家庄 050003;(3.陆军工程大学指挥控制学院,南京 211101)
0 引言
全军坚持把军事训练摆在战略位置,不断提高部队实战化水平。“实战演训、科学演训”成为当下部队提高战斗力的一个重要课题。针对摩托化机动演训问题,借助信息化技术,可以实时获取演训数据,基于数据分析的演训效果评估对提高部队演训水平和指挥决策能力具有重要意义[1],它可为机动部队指挥员、驾驶员提供反馈,是贯彻落实“以评促备、以评促训、以评促建”的有效手段,具有极大的军事实用价值和广泛的军事应用前景。
当前,定量评估在装备保障训练中的运用已较为成熟[2-3],但在实战演训中的研究与应用却较少。早期,国内专家通常借助宏观认识、经验积累来评判演训效果;随着信息化技术发展,不少学者提出要精准量化,完善标准体系。齐霁简要介绍了《千分制检验评估实施细则》[4],指出引入数理分析和统计学原理等理念,能较好解决传统评估不精准的问题,同时也提到《千分制》的顶层设计,虽较为完备,但多级下层的实战导向特征不明显,仍需在指标体系和评估方法上不断完善;此外,不少文献论述了演训定量评估的重要性,并讨论了建立指标体系时应注意的关键点,但大都缺乏系统性和应用性论证。本文提出以目标导向实施演训效果评估,流程图如图1 所示。针对摩托化机动演训问题,首先以实战导向确定关键能力要素,进而建立评估指标体系以及确定各指标权重,同时,依据各能力要素设计需要的可量化指标数据获取途径,可选择直接采集或间接转换,最后将数据代入评估模型进行综合评估,以实现演训效果反馈的目的。
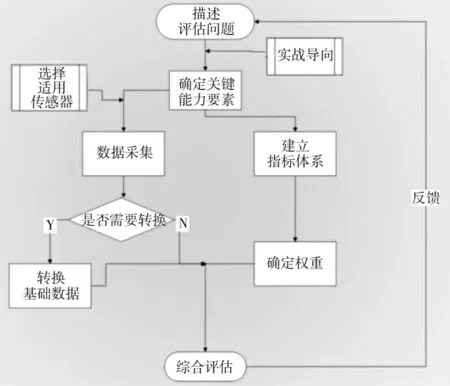
图1 演训效果评估流程图
1 指标体系的建立
1.1 指标体系建立的原则
演训应当以实战导向为目标,同时在数据的收集和处理上,需充分考虑现有传感器技术的普适度以及方法处理效率,因此,建立指标体系时应遵循以下原则:1)完备性原则,指标体系需要充分反应实战要求下的各项能力;2)层次性原则,应当清晰界定各项能力的评价指标构成,做到科学划分;3)可比性原则,各项指标的计算应当规范,使用同一标准;4)可操作原则,应考虑各项指标的数据获取难度,尽可能做到充分利用;5)可视化优先,各项指标数据应能有效展示,提升指挥决策效率。
1.2 指标体系的建立
遵循演训评估指标体系建立的原则,充分反映摩托化机动实战导向,对投送部队的指挥控制能力、保障能力及协同能力3 项主要能力要素进行综合评估。其中,指挥控制能力包括对投送部队任务执行效率、规范性和安全性3 方面能力进行考量,保障能力则可以从对象维度分为道路保通、人员保障和装备保障3 项要素,协同能力从时间维度上,主要分为行动前和行动中投送部队与相关单位的协调能力,最后,综合考虑评估过程的实操性和数据获取的效率,建立包含3 个准则层、8 个1 级指标、15 个2 级指标的评估指标体系,如表1 所示。

表1 摩托化机动演训评估指标体系
1.3 指标体系的说明
下面对表1 中2 级指标层各要素进行说明。平均速度D1 反映分队的行进执行力,可用总里程除以累计行驶时间求得,为正向指标;启动效率D2 反映分队的出动执行力,可用车队整体出发时间(头车出发到尾车出发)除以分队车辆数求得,为反向指标;制动效率D3 反映分队的制动执行力,可用分队整体制动时间(头车停止到尾车停止)除以分队车辆数求得,同样为反向指标。车间距D4 及休息时长及频率D5 主要与演训规范标准作比较[6],车间距可用头车与尾车的距离除以车辆数求得,与规范标准越接近,表示越佳,反之越差。高速行进方位角变化率D6 反映高速行进过程中的队形方位角变化幅度,可用头车和尾车的方位角度差的变化除以时间变化求得,该指标控制在合理区间内,说明驾驶越安全,反之越危险,为反向指标;电磁干扰静默态势D7 反映机动过程中的反电子侦察能力[7],在实践中,可不定期对摩托化机动分队进行实战化电子侦察,用平均信号强弱度量该能力[8],指标越大,则说明该项安全防护能力越差,反之越强,为反向指标。保障层与协调层指标较易理解,此处不再赘述。
2 基于AHP-熵值法的评估模型建立
利用上述演训评估指标体系,本文采用AHP 法对演训效果进行综合评估,同时,在确定各项指标权重上,除参考AHP 法原有的专家打分外,引入熵值法对各项指标再次进行客观定权,最后由专家赋权和客观赋权综合计算最终权值。
2.1 专家赋权——AHP 法
AHP 法是一种解决复杂层次结构评估问题的有效方法,它用一定的标度对专家的主观判断进行量化[9],逐层检验比较结果的合理性,最后依据各指标最终权值代入数据进行综合评估。针对演训问题,首先采用AHP 法确定指标的主观权重,即专家赋权,该权重确定方法的主要思路如下:
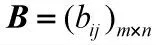

表2 1-9 标度的含义


表3 1-9 阶矩阵的平均随机一致性指标
3)层次总排序及一致性检验。利用同一层次中所有层次单排序的结果,计算层次总排序wi。而后计算总排序一致性指标CI,并比对总排序随机一致性指标RI,方法与单层一致性检验类似。检验通过,即确定出专家赋权的各指标权重。
2.2 客观赋权——熵值法
熵是信息论中测定不确定性的量[10],针对演训问题,若各投送部队在某些能力指标上差异越大,则应予以更加重要的关切,相反,若差异越小,则对整体评估影响越小,这种基于数据出发客观确定指标权重的方法,可在专家打分的基础上进行综合和修正,提高容错率。熵值法的计算过程为:
1)将xij做正向标准化处理(即标准化数值越大,表示越佳),此处采用理想点法。
对于正向指标,


2.3 综合权值的确定
AHP 法侧重于专家的主观偏好,熵值法侧重于挖掘数据本身的客观信息,两种方法各有利弊[11]。为保证摩托化机动演训评估的专业性,同时希望评估结果更加客观,本文采用AHP-熵值法线性加权确定评价指标的综合权重为:

式中,β 为偏好系数,w1为专家赋权,w2为客观赋权;且0 ≤β≤1。这里认为专家对于各项能力要素的专业判断较为准确,因此,选取系数β 为0.6。
3 算例分析
某部队领取上级命令,采取摩托化行军的方式开展机动演训,要求5 个分队从同一城市出发,在规定时间内到达目标地点。分队车辆安排情况:第1分队54 辆机动车,第2 分队58 辆机动车,第3 分队51 辆机动车,第4 分队55 辆机动车,第5 分队62 辆机动车。在各分队头车和尾车安装数据记录仪,从部队机动开始后每10 s 记录数据,包括经度、纬度、高程、速度、里程和方位角共6 项基础数据,演训结束后,将数据导出。某分队采集的部分基础数据如表4 所示,现对5 个分队的演训效果进行评估。
3.1 数据可视化
为增强对摩托化机动全过程的直观把控,在进行评估前,运用Python3.4 对5 个分队6 d 的机动线路进行可视化呈现,部分视图如图2~下页图3 所示。
由图分析得到,5 个分队的出发位置、到达位置和机动线路均大致相同,但在时序上存在明显差异,可理解为该次演训任务由上级统筹协调,各分队依次执行实施,故此算例不必考虑各分队的保障能力和协调能力,主要对各分队的指挥控制能力进行评估,此外,算例中未进行实战化电子侦察操作,故该项指标也不予考虑。
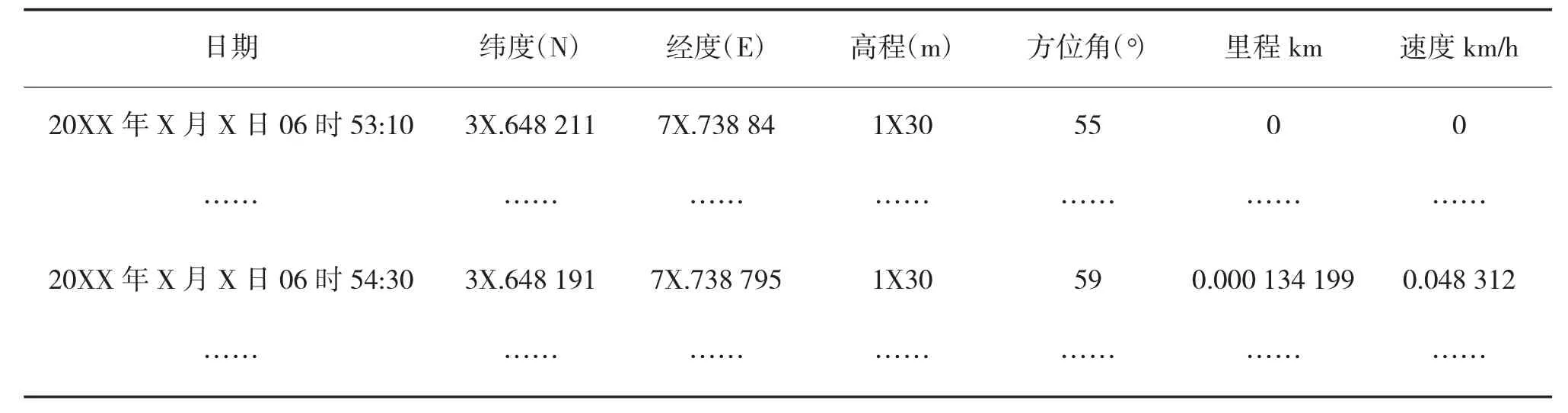
表4 算例部分基础数据

图2 第1 分队6 d 的机动路线(经度、纬度、高程)

图3 第1 d 与最后1 d 5 个分队的机动情况(时间、纬度、高程)
3.2 演训效果评估
根据演训评估指标体系,此处就分队指挥控制能力建立评估模型如图4 所示。
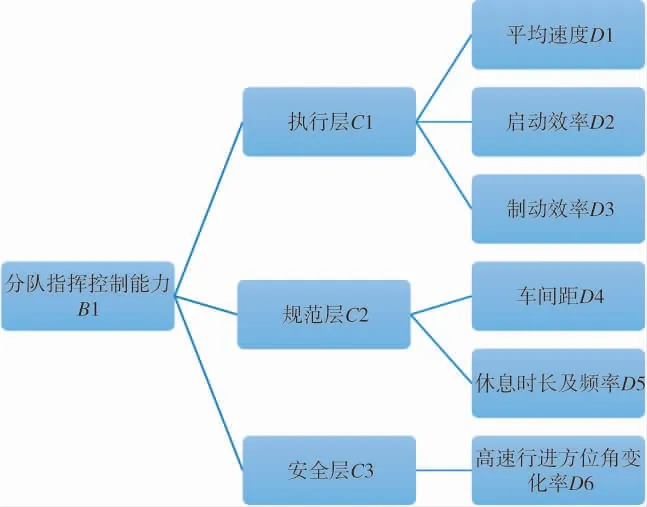
图4 分队演训指挥控制能力评估模型
1)数据转换及标准化
首先对传感器采集的基础数据进行转换。分析头车、尾车传感器的位置、时间变化,可以确定车队的整体出发时间、整体制动时间,以及行进中休息的时长与频率等潜在信息,进而根据基础数据及挖掘信息转换求得各指标数值,这里,在得到车间距D4 及休息时长及频率D5 后,需进一步与规范标准作差并取绝对值,最后再对各指标属性(正向或负向)进行区分,按照上文理想点法式(1)、式(2)对指标数值进行标准化,得到处理后数据如表5 所示。1表示最优,0 表示最次,标准化数值越大表示该项指标越佳。
2)运用AHP-熵值法确定指标综合权值
步骤1:首先根据专家经验对层次各要素相对重要性进行打分,包括B-C,C1-D,C2-D,其中,实战要求越高则越重要,得到相应判断矩阵B、C1、C2,并计算各要素权重。

运用Matlab2018 计算得到各层指标权重如下:
ωB= (0.637 0,0.258 3,0.104 7),CI=0.019 3,CR=0.033 2<0.1,通过一致性检验;
ωC1= (0.625 0,0.238 5,0.136 5),CI2=0.0091,CR2=0.015 8<0.1,通过一致性检验;
ωC2=(0.333 3,0.666 7)。
则层次总排序为:

表5 标准化数据

步骤4:求得5 分队最终评估得分p=(0.532 2,0.494 0,0.505 4,0.350 3,0.246 0),得到各分队机动演训指挥控制能力的排名为:1 分队>3 分队>2分队>4 分队>5 分队。
经分析,1 分队在执行层3 项指标上远胜过其他分队,因此,总分排第1 名,但是车间距及高速行进方位角变化排末位,这拉低了总分,导致与第2名差距不大,反映出1 分队的执行能力较强,但对于规范性与安全层等细节问题,后续需要注重改善;3 分队的休息次数及频率控制最优,制动效率第2 名,其余指标均处于中等,各项能力较为均衡,因此,总分略胜过2 分队,排第2 名;2 分队的安全层能力最佳,平均速度、车间距排第2 名,启动效率排末位,其余指标处于中下,总分排第3 名,后期可首要针对启动效率加以训练;4 分队执行层各指标较差,休息次数与频率控制排第2 名,其余指标处于中等,总分排第4 名,后期应以实战为导向,着重提升执行层能力;5 分队休息次数与频率控制最差,车间距最佳,但是其余指标均处于中下,因此,总分排名末位,后期需要在保证车间距规范基础上,提升其他各项能力。
3.3 方法对比
单独运用AHP 法主观赋权,最终得分p'=(0.589 1,0.508 9,0.507 2,0.314 6,0.223 5),各分队排名:1 分队>2 分队>3 分队>4 分队>5 分队;
单独运用熵值法客观赋权,最终得分p''=(0.446 8,0.471 7,0.502 6,0.403 9,0.279 7),各分队排名:3 分队>2 分队>1 分队>4 分队>5 分队;
对比发现,单独使用AHP 法,则执行层权重过大,导致1 分队得分虚高,不利于分析演训存在的问题;而单独使用熵值法则违背了能力重要性的专业判断。因此,利用AHP 法专家打分首先确定各指标重要性,而后运用熵值法对主观权重进行修正的方法在演训评估问题中具有可操作性,且准确度更高。
4 结论
针对演训评估问题,首先需要结合案例背景,以实战导向建立评估指标体系,同时,在大数据环境下,充分运用物联网技术,具有针对性地采集相关数据,进行评估分析,以起到良好的训练反馈作用,提升演训效果。基于AHP-熵值法的评估方法可操作性较强,且更加符合实际情况,有助于发现问题,为决策提供参考;但对于综合赋权β 值的选取有待进一步优化。后期,需收集更多的案例数据,试采用BP 算法对该问题进行深入研究[12],这也将是下一步工作的重点。

