适用于复杂动态环境的智能车运动规划方法

李 卓，姚立泽，王丽霞，刘福聚

（1.北京交通运输职业学院汽车工程系，北京102618；2.长春职业技术学院汽车学院，吉林 长春 130011；3.中国汽车技术研究中心有限公司业务发展部，北京100070）

1 引言

汽车持有量的增加带来了道路拥挤、环境污染、交通事故等诸多问题，智能车自动驾驶技术为这些问题的解决带来了契机[1]。运动规划是自动驾驶技术的重要研究方向，是实现自动驾驶的前提。

根据对工作环境的掌握程度，运动规划分为全局规划和局部规划；根据工作环境障内碍物运动情况，运动规划分为动态规划和静态规划。运动规划常用方法有可视图法、自由空间法、Dijkstra 算法、人工势场法、智能算法等，可视图法要求工作环境简单，当障碍物较多时搜索时间过长[2]；Dijkstra 算法对目标点启发信息使用较少，导致算法规划路径时间较长[3]；人工势场法能够较好躲避障碍物，但是存在目标点不可达和局部极值问题[4]；智能算法应用于运动规划是当前主要发展方向，应用智能算法规划的路径较优，存在的问题主要集中在算法自身缺陷上。

目前运动规划成果大都集中在静态环境中，动态环境下运动规划方法相对较少且不成熟，以人工势场法为基础，针对算法自身缺陷和动态环境适应性进行了改进，使智能车能够躲避动态障碍物、跟踪动态目标点，得到了适用于动态环境的动态人工势场法，经验证此方法能够使智能车在动态环境中安全行驶。

2 传统人工势场法

在人工势场中，目标点对智能车产生引力势场，障碍物对智能车产生斥力势场，工作环境中任意点的势场为引力势场和斥力势场的矢量和，势场力为势力场的负梯度值，智能车在势场力的牵引下，到达目标点。

2.1 引力势场与引力

记智能车位置为XR，目标点位置为XG，障碍物位置为XO，智能车受到的斥力场记为Urep（XR），引力场为Uatt（XR），综合势场为U（XR）。

目标点对智能车的引力势场大小与两者距离有关，距离越大则势场越强，引力势场Uatt（XR）构造方式如下[5]：

式中：Ka—引力势场增益系数；d（XR，XG）—智能车与目标点间的欧式距离。

则根据力与势场的换算关系可知，目标点对智能车的吸引力为：

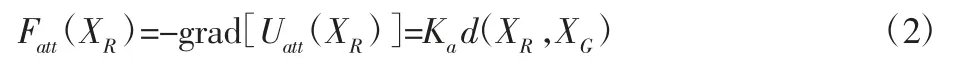
式中：grad（）—梯度计算。引力方向为智能车指向目标点。

2.2 斥力势场与斥力

当障碍物与智能车距离越近时，斥力势场越强，斥力也就越大，当两者距离越远时，斥力势场越弱，斥力也就越小，当两者距离超过一定范围时，斥力势场消失，则斥力势场构造为[6]：

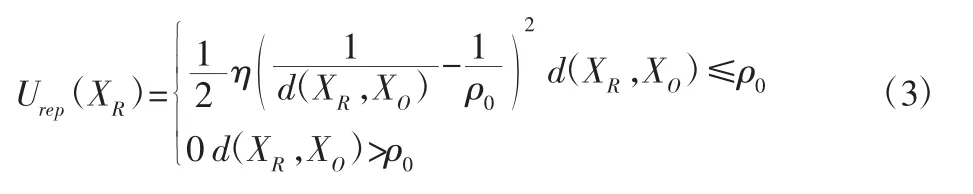
式中：η—斥力势场增益系数；ρ0—斥力势场作用范围临界值。根据斥力势场给出斥力为：

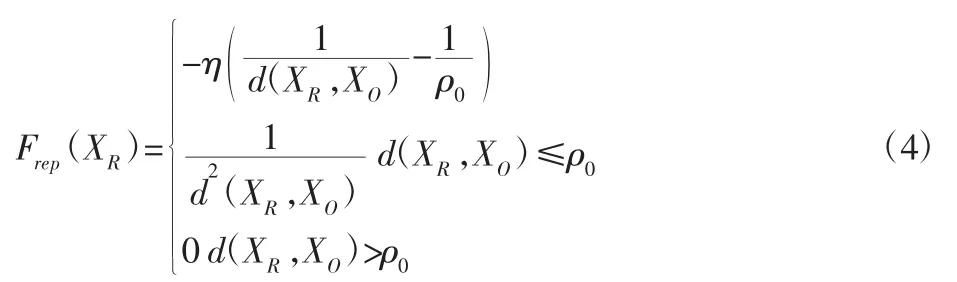
其中负号表示斥力方向与引力方向相反。

2.3 综合势场与合力

智能车在任意一点受到的综合势场作用为引力势场和斥力势场的矢量和，即：

智能车在任意一点受到的合力既可以通过综合势场求得，也可以通过引力与斥力的矢量和求得，合力方向使用平行四边形准则确定，如图1 所示。

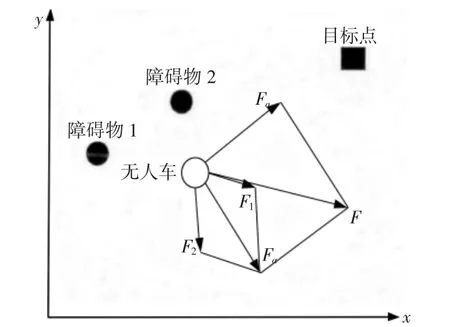
图1 多个力求合力的平行四边形规则Fig.1 Composition Method of Multiple Forces

3 算法自身缺陷的改进

3.1 局部极值陷阱及虚拟水流法改进

人工势场法的本质是，智能车在合力作用下，沿着势场减弱的方向运动到目标点。但是在特定环境中，由于障碍物数量及排列方式的不同，会使某些点位的合力为0，此时智能车陷入局部极值陷阱，从势场角度讲，此时智能车位于势场的局部极小值点[7-8]。

使用虚拟水流的思想解决这一问题，主要使用水流的两个特性：（1）当水流至凹处时，就开水注水，直至水流高度超过周围高度则进行流动；（2）水往低处流。使用类比法，智能车起始位置为人工水源，将工作环境中智能车受到的综合势场比作地势，局部极值陷阱即为凹处，当水流至凹处时，向此处注水就相当于增加此处的势场，当凹处势场足够大时，继续向势场减小的方向前进，直至到达势场最小位置（也即目标点）。

根据以上分析，虚拟水流法对人工势场法的改进分三个步骤实现：

（1）判断智能车是否陷入局部极值陷阱。

智能车陷入局部极值时，表现为在某处振荡或转圈。为了给出局部极值陷阱的判定方法，首先给出邻域位置集的概念。记为智能车在单位时间内能够到达的位置，则所有的集合称为智能车当前位置XR的邻域位置集，记为那么当：

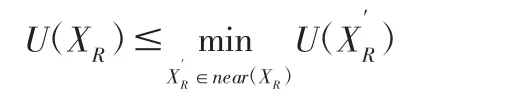
成立且此处不是目标点时，说明智能车陷入了局部极值陷阱；若上式不成立，说明智能车未陷入局部极值陷阱。

（2）模拟注水过程，增大局部极值处的势场。

智能车在局部极值陷阱处受到的总势场调整为：

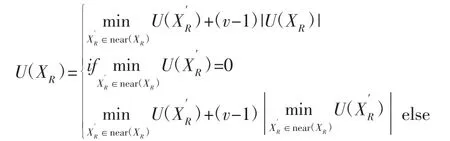
式中：要求v-1>0，代表“注水”过程。

（3）选择邻域位置集最小势能点作为前进方向。

经过第2 步注水过程，局部极值陷阱处的势能不再是局部极值，按照“水往低处流”的原则，智能车选择邻域位置集的最小势能点作为前进方向，这样就跳出了局部极值陷阱，而后按照人工势场法继续前进，直至到达目标点。

3.2 目标不可达及斥力势场改进

按照传统人工势场法中对引力和斥力的定义方法，当智能车靠近目标点时。目标点对智能车的引力作用会减小，若目标点附近存在障碍物，障碍物对智能车的斥力就会占主导地位，使智能车在目标点附近徘徊而无法到达目标点[9-10]。

为了解决这一问题，将智能车到目标点的距离引入到斥力势场中，使得智能车接近目标点时，目标点对智能车的引力占主导地位。具体改进方法为：

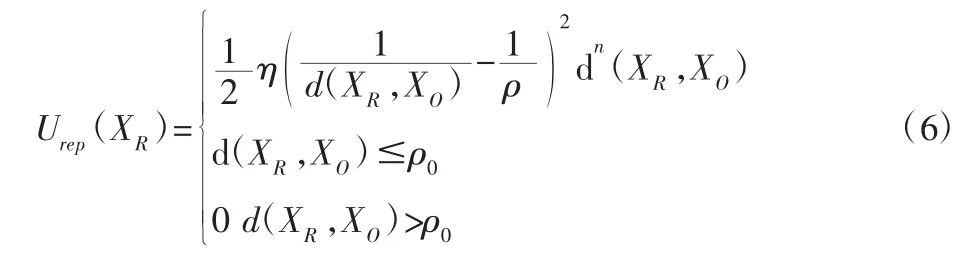
式中：要求n∈（0，1）。对斥力势场求负梯度，得斥力为：

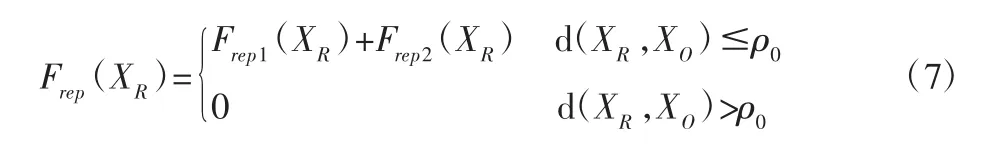
其中，将斥力Frep（XR）分为是因为两个力的形成原因和方向不同。其中由斥力势场对d（XR，XO）求偏导所得，为：

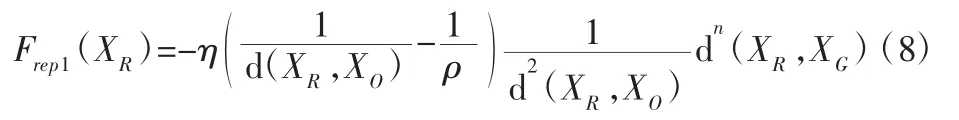
此力的方向由障碍物指向智能车。

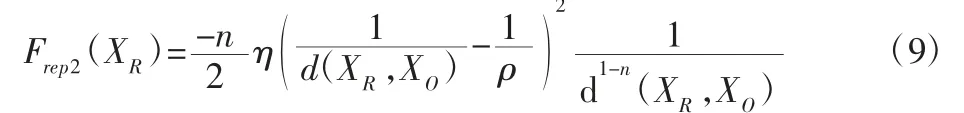
此力的方向为由智能车指向目标点。

分析Frep1（XR）和Frep2（XR）可知，当智能车靠近目标点时，d（XR，XO）逐渐减小并趋于0，则Frep1（XR）也趋于0，而Frep2（XR）趋于无穷大，从力的角度讲，当智能车靠近目标点时，障碍物斥力Frep1（XR）不起主导作用，而力的分量Frep2（XR）起主导作用，吸引着智能车逐渐向目标点靠近，直至到达目标点后，无穷大的吸力将智能车牢牢吸附在目标点。

3.3 改进方法的算法流程图

基于3.1 节和3.2 节对局部极值和目标不可达问题的改进，给出改进算法流程图，如图2 所示。

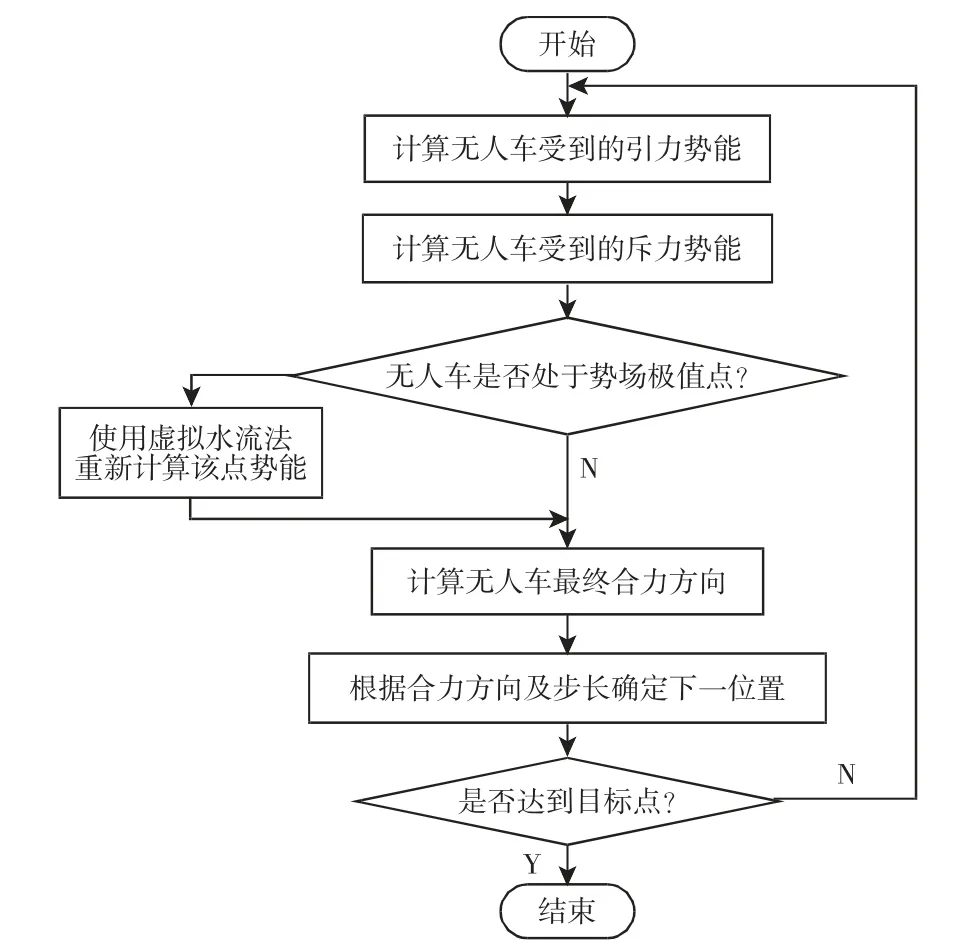
图2 改进人工势场法流程图Fig.2 Flow Chart of Improved Artificial Potential Field

4 适用于动态环境的动态势场法

上节对算法的改进克服了传统算法自身缺陷，但是改进算法中目标点引力和障碍物斥力只考虑了位置因素，引力和斥力的构造中没有考虑对目标点和障碍物速度、加速度的趋向或避让，因此上节的改进算法只适用于静态环境。智能车的运行环境大都是动态环境，因此在上节改进的基础上，在引力和斥力中引入速度、加速度因素，从而提出适用于动态环境的动态人工势场法。

4.1 引力势场与引力函数

在动态环境中，引力势场不仅要考虑智能车与目标点的相对位置因素，还要考虑相对速度因素，得改进式为：

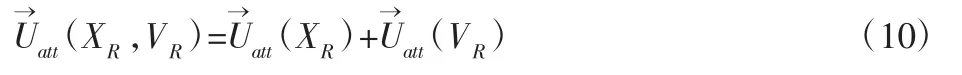
式中：Kv—引力势场速度增益参数；VR—智能车速度；VG—目标点速度。则引力的合力为：

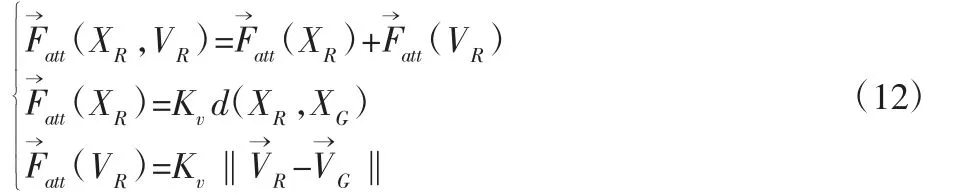
4.2 斥力势场与斥力函数

在动态环境中，障碍物对智能车的斥力作用，不仅要考虑位置因素，同时还要考虑速度因素和加速度因素。在式（3）对斥力势场改进的基础上，适用于动态环境的斥力势场为：

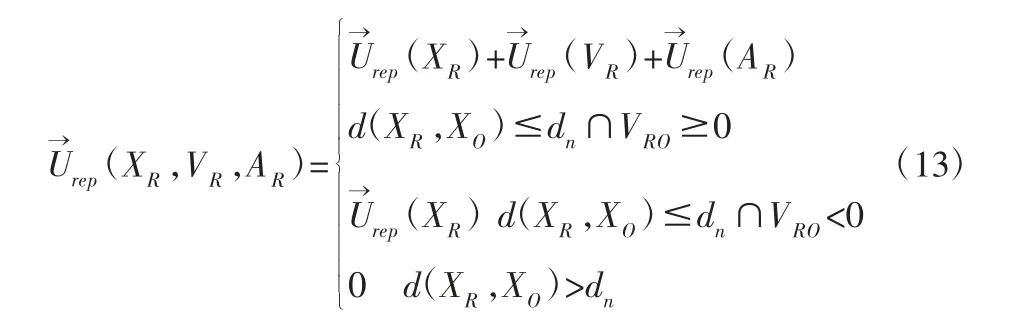
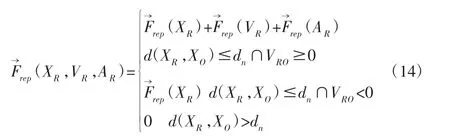
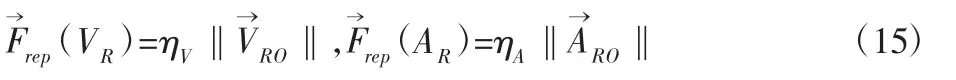
4.3 综合势场与合力

适用于动态环境的综合势场为动态引力势场和动态斥力市场的矢量和，即：

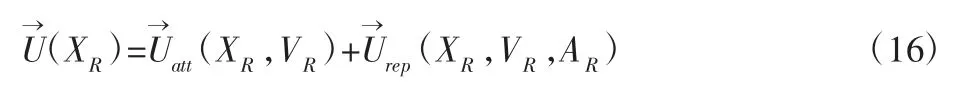
当智能车陷入局部极值陷阱时，依然使用虚拟水流法解决，注水过程及表达式与3.1 节中完全一致。

适用于动态环境的合力为引力和斥力的矢量和，为：

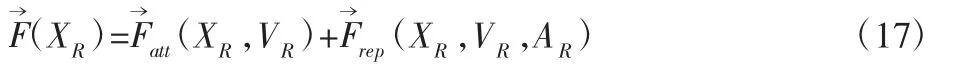
合力的方向即为智能车前进的方向。

4.4 基于动态人工势场法的运动规划流程图

第3 节针对算法自身缺陷进行了改进，本节在第3 节改进基础上，进行了动态环境适应性改进。结合两节的改进内容，给出基于动态人工势场法的运动规划流程图，如图3 所示。

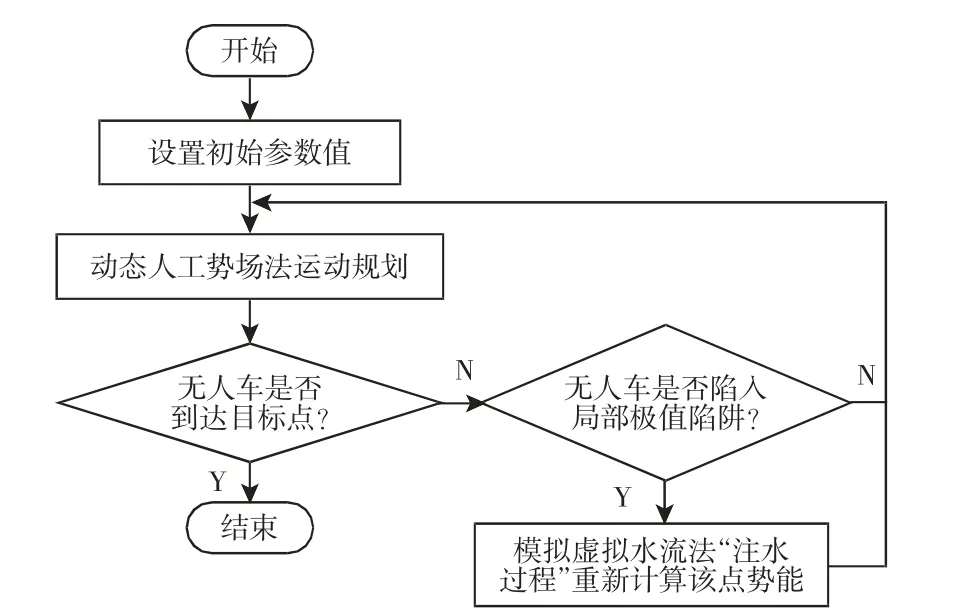
图3 基于动态人工势场法的运动规划Fig.3 Flow Chart of Motion Planning Based on Dynamic Artificial Potential Field

5 仿真验证

仿真验证分为三个部分，一是验证虚拟水流法能够使人工势场法逃出局部极值陷阱；二是验证斥力势场函数的改进可以解决目标不可达问题；三是验证动态人工势场法适用于动态环境，能够规划出无碰路径。

5.1 仿真一：局部极值陷阱问题验证

此部分构造出一个含有局部极值陷阱的工作环境，如图4（a）所示。智能车起始位置为（2，0），目标位置为（4，5），智能车步长设置为0.4，斥力影响范围阈值设置为dn=2，引力势场增益系数Ka=2.5，斥力势场增益系数η=5.4。为了构造局部极值陷阱，在工作环境中安放了33 个障碍物，每隔0.05 排列成拱形，如图4 所示。图中矩形表示智能车在不同时刻留下的轨迹，圆形为障碍物，“*”为目标点。

则使用传统人工势场法和虚拟水流法改进的人工势场法分别进行运动规划，结果如图4 所示。

分析图4 可知，图4（a）中，智能车最后一个位置为局部极值陷阱，到达此位置后智能车受力为0，无法继续前进。此时改进算法模拟虚拟水流法注水过程，使极值陷阱处势场增大，而后向势场最低处前进，以此来摆脱局部极值缺陷。

图4 局部极值缺陷问题验证Fig.4 Local Extremum Trap Problem Clarification

5.2 仿真二：目标不可达问题验证

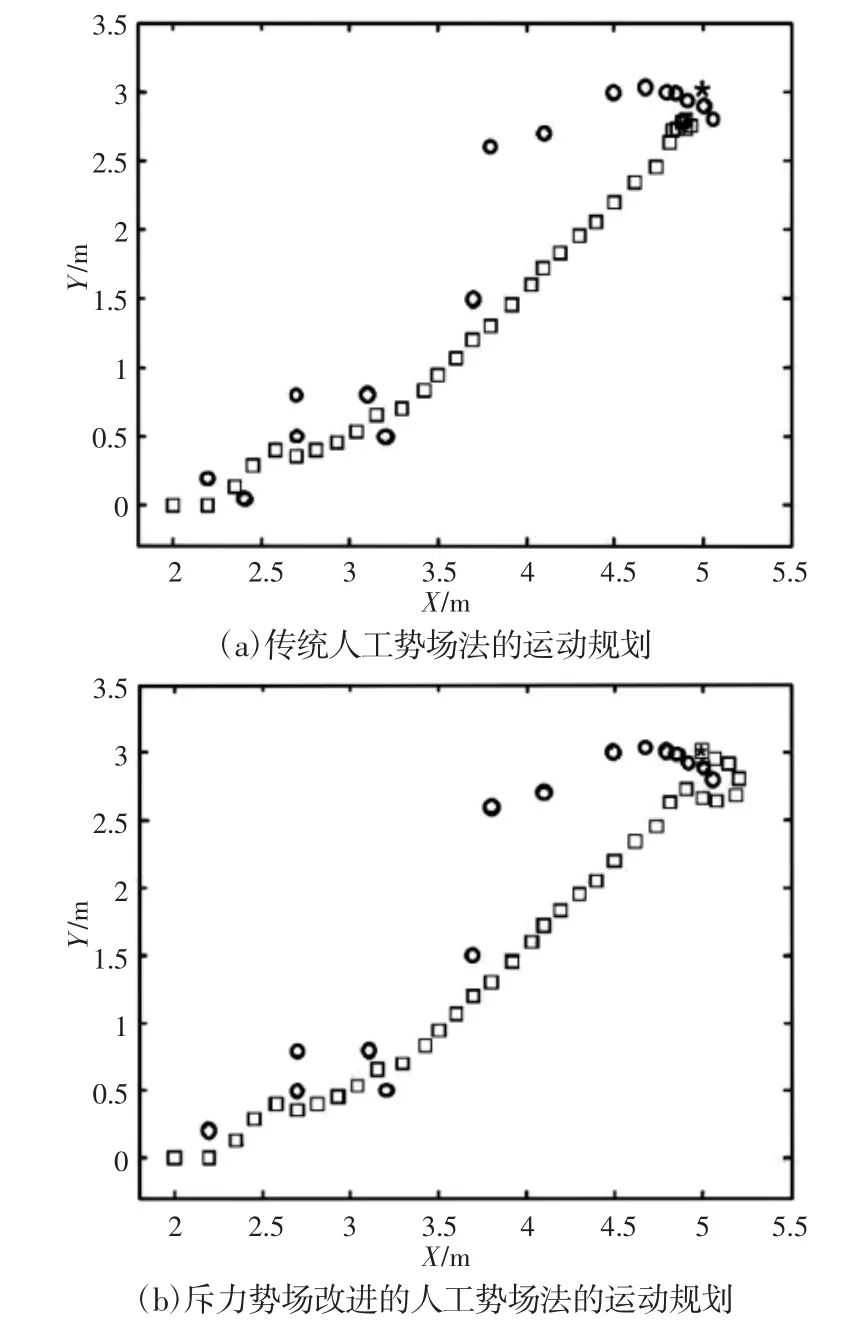
图5 目标不可达问题验证Fig.5 Goal Unreachable Problem Clarification

目标不可达问题是因为目标点附近存在障碍物，为了验证对目标不可达问题的改进，此部分超构造的工作环境，如图5 所示。图中：圆圈—障碍物；方形—智能车；星号—目标点，智能车起始点为（2，0），目标点为（5，3），智能车步长设置为0.1，斥力影响范围阈值设置为dn=2，引力势场增益系数Ka=2.5，斥力势场增益系数η=5.4。为了构造出目标不可达问题，在目标点附近安置了6个障碍物。分别使用传统人工势场法和改进人工势场法在此环境中进行运动规划，结果如图5 所示。

从图5（a）可以看出，由于目标点附近存在障碍物，当智能车接近目标点时，目标点的引力减小，而障碍物的斥力增加，最终合力方向使智能车远离目标点；智能车远离目标点后，引力作用增加，而斥力减小，合力方向使智能车向目标点靠近，如此反复形成了智能车在目标点附近徘徊的现象。

而斥力势场改进的人工势场法，当智能车接近目标点时，虽然目标点的引力作用减小了，但是斥力势场产生的力的分量Frep2（XR）逐渐占据主导地位，使得智能车逐渐靠近目标点，并最终到达目标点。

5.3 仿真三：动态环境下运动规划

构造一个复杂动态环境，如图6 所示。图中：方块—智能车；圆点—目标点；物体—障碍物，其中C1、C2为动态障碍物，C1运动方向为-150°，一步步长为0.1（与机器人步长单位相同），C2运动方向为0°，步长为0.05。智能车起始位置为（4，10），目标位置为（15，3），智能车步长设置为0.2，斥力影响范围阈值设置为dn=2，引力势场增益系数Ka=2.5，斥力势场增益系数η=5.4，水流速v=2。

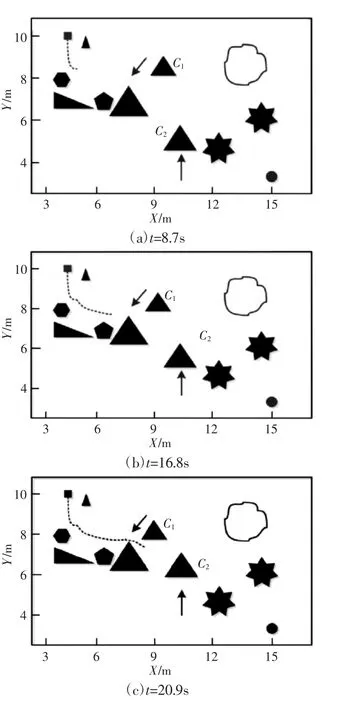
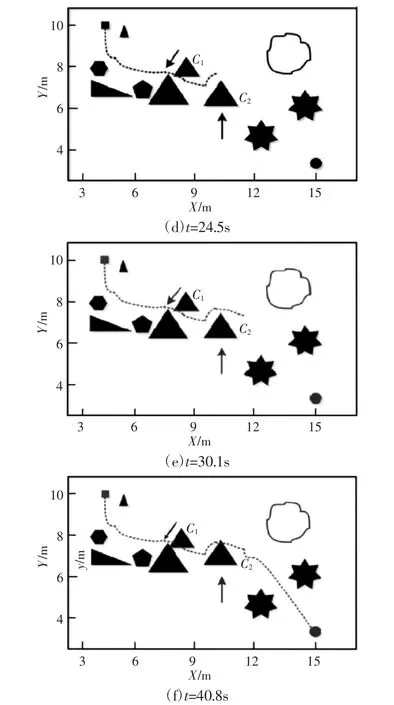
图6 复杂动态环境中智能车运动轨迹Fig.6 Intelligent Vehicle Motion Path under Complex Dynamic Environment

在此复杂动态环境中，智能车的运动过程，如图6 所示。图6给出了某几个关键时刻智能车的运动状态，图中黑色虚线表示智能车的行驶轨迹。智能车在运动过程中，边运动边检测障碍物，对于静态障碍物，使用式（6）给出的斥力势场函数，对于动态障碍物则使用式（13）给出的动态斥力势场函数；当检测到目标时，静态目标点使用式（1）给出的引力势场，动态障碍物使用式（11）给出的动态引力势场函数。智能车在运动过程中，边进行规划边检测是否陷入局部极值陷阱，陷入局部极值陷阱时，使用虚拟水流法进行注水从而逃出陷阱位置。最终智能车运动轨迹，如图6 所示。在t=8.7s，智能车在目标点引力和障碍物斥力作用下，到达所示位置；t=16.8s 时，智能车在避开静态障碍物的同时，检测到动态障碍物C1，使用动态斥力势场函数用于躲避动态障碍物；t=20.9时，智能车成功避开动态障碍物C1，继续前进；t=24.5s 时，智能车检测到动态障碍物C2，使用动态斥力势场函数进行避障，由于C2不断靠近障碍物，所以C2对智能车的斥力包括位置因素、速度因素、加速度因素；t=30.1s 时，智能车成功避开动态障碍物C2，同时检测到目标点，目标点为静止状态，使用传统引力势场函数；t=40.8s 时，智能车成功到达目标点。

6 结论

从两个方面对传统人工势场法进行了改进：（1）针对算法自身存在的缺陷，使用虚拟水流法和改进斥力势场的方法，解决了局部极值和目标不可达问题；（2）对算法进行了动态环境适应性改进，使算法能够躲避动态障碍物、跟踪动态目标点。经验证，基于动态人工势场的运动规划方法能够在复杂动态环境中规划出安全路径，保证智能车安全行驶。下一步的研究方向为路径的精确跟踪，此部分内容在这里未做研究。