基于响应面法的薄壁梁耐撞性多目标优化

吴胜军，叶欣钰

（湖北汽车工业学院汽车动力传动与电子控制湖北省重点实验室，湖北 十堰 442002）

1 引言

由于金属薄壁梁成本低，而且有着良好吸能特性，被广泛应用到航空航天、船舶、车辆等交通工具的碰撞吸能装置中[1-2]。薄壁梁作为客车车身骨架基本组成构件，在发生碰撞时能吸收大量的能量，因此对金属薄壁梁耐撞性的研究有着重大的意义。国内外很多学者运用RADIOSS，LS-DYNA，PAM-CRASH 等有限元分析软件，研究薄壁梁的碰撞作用力和性能，包含薄壁梁厚度、截面形状以及材料对其性能的影响[3-5]。文献[6-7]研究了带有不同填充材料如泡沫铝、蜂窝铝的薄壁梁的吸能特性。文献[8]研究了多材料轻量化薄壁结构，研究表明该结构可以很好的应用到汽车车体结构当中，起到很好的节能环保作用。文献[9]研究了锥角、厚度和吸能槽对锥形薄壁梁碰撞性能的影响，研究结果表明吸能槽数量越多，锥角角度中等和厚度越小的薄壁梁可以获得更大的碰撞力效率，而吸能槽数量越少，厚度越大，锥角角度越小，则能获得更大的比吸能。文献[10]分析了不同截面薄壁梁单一结构和多胞结构的吸能能力，结果表明多胞结构的薄壁梁吸收的能量大于单一结构的薄壁梁，其中六边形和八边形的多胞结构比鼻梁的比吸能最大。这里主要是从优化薄壁梁的基本参数，替换更好的吸能材料，增加诱导结构这三个面综合提升薄壁梁的耐撞性。碰撞是一个高度非线性问题，如材料非线性、几何非线性以及接触非线性，运用一般的规划方法很难求出最优解。而响应面法是一种实验条件寻优的方法，能很好的解决这类问题。

在研究碰撞性能中，使用全因子试验法设计试验点，基于Hyperworks 与Ls-dyna 联合仿真求解。根据得到的结果，基于设计变量，运用最小二乘法拟合得到比吸能、碰撞力峰值力与变形量的多目标响应面模型，利用Matlab 优化函数求解。最后基于优化后的结果，替换铝合金材料，增加诱导槽结构，进行仿真，将前后的结构进行对比分析。

2 有限元模型的建立及参数确定

2.1 有限元模型描述

考虑到碰撞问题的高度非线性与复杂性，使用Ls-dyna 软件分析不同截面参数的薄壁梁碰撞响应。薄壁梁有限元模型，如图1 所示。由于在实际应用中，薄壁构件后面通常连接着质量相对较大的物体，因此在仿真分析时薄壁梁末端附加200kg 质量。薄壁梁以30km/h 的速度撞击刚性墙。薄壁梁采用BT 单元，厚度方向上进行5 点积分。

图1 薄壁梁有限元模型Fig.1 Finite Element Model of Thin-walled Beam

2.2 材料选择

薄壁梁材料为Q235 结构钢，本构模型选用汽车中广泛使用的MAT24 号材料，密度ρ=7900kg/m2，弹性模量E=210GPa，泊松比ν=0.3，屈服应力为235MPa。

2.3 摩擦参数的确定

有限元计算式要考虑边界摩擦与内部摩擦的影响，薄壁梁与刚性墙之间的摩擦即为边界摩擦，摩擦因数定义为1；薄壁梁自身的摩擦为内部摩擦，一般结构钢的内部摩擦因数为0.2。

2.4 网格大小的确定

方形薄壁梁的折弯半径大致可以用r=0.72c1/3t2/3进行计算[11]，式中：c—截面宽；t—薄壁梁厚度，要精确的描述变形，网格尺寸要<0.5πr。因此，网格尺寸确定为3mm。

3 优化设计

3.1 优化问题描述

在碰撞过程中，碰撞加速度与生存空间是评价安全性的两个主要指标。而薄壁梁作为许多交通工具的主要碰撞吸能装置，应当充分考虑这两个因素。因此，将薄壁梁的比吸能SEA、最大碰撞峰值力Fm和变形量L 作为优化目标。而且，截面边长a 与薄壁梁的厚度t 作为薄壁梁的两个主要参数，在一定范围内取值作为优化的设计变量。这里a 的取值范围为（40～60）mm，t 的取值范围为（2～4）mm。对于这里的多目标优化问题可定义为：

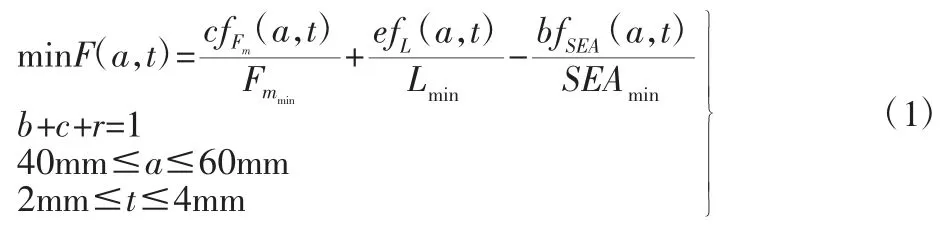
式中：b、c 和e—权重系数；fSEA—比吸能函数；fFm—最大碰撞峰值力函数；fL—变形量函数。

3.2 响应面法

在现在工业中，响应面法广泛地应用到结构的改进与优化中。响应面法[12]是试验设计与数理统计相结合的方法。首先确定试验设计点，分别对这些试验点进行仿真分析，产生于试验点相对应的输出响应，利用最小二乘法，将这些响应拟合成响应面，然后在响应面上进行最大梯度寻优。使用响应面法用来确定使目标函数最小的薄壁梁截面参数。加权后的目标函数作为薄壁梁的响应，可以近似用以下函数形式进行拟合：

式中：n—基本函数φi（a，t）的个数；

βi—回归系数。

式（2）中的回归系数用最小二乘法求得。最小二乘法可用下式表达：

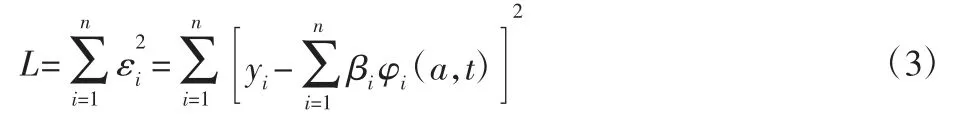
式中：εi—响应值与拟合值之间的误差。

因此，回归系数向量b=（β1，β2，…，βi）可由来确定。

所以：

式中：Φ—试验点的矩阵，包含m 个试验点。

通过式（2）与式（3），响应面模型能够完全确定下来。而响应面模型的精确性可根据判定系数R2，调整的判定系数与平均相对误差来评价。由经典响应面理论可得越接近于1，平均相对误差越小，则响应面模型的拟合程度越高。

3.3 仿真分析

基于优化问题的定义，在a 与t 的设计范围内，采用六级全因子设计进行取样，使得6×6 设计点均匀分布在设计范围内。每个试验点建立相应的有限元模型，仿真分析得到变形量与碰撞峰值力。仿真结果，如图2 所示。仿真结果数据，如表1 所示。

图2 碰撞变形图Fig.2 Collision Deformation Diagram of Thin-walled Beam

3.4 优化分析

基于仿真数据，根据最小二乘法拟合出SEA、Fm 以及L 的函数，表达式如下：

拟合函数fSEA、fFm和fL的R2与平均相对误差值，如表2所示。由表2 可知，R2和都趋近于1，而平均相对误差接近于0，所以响应面模型构造合理，下一步优化切实可行。

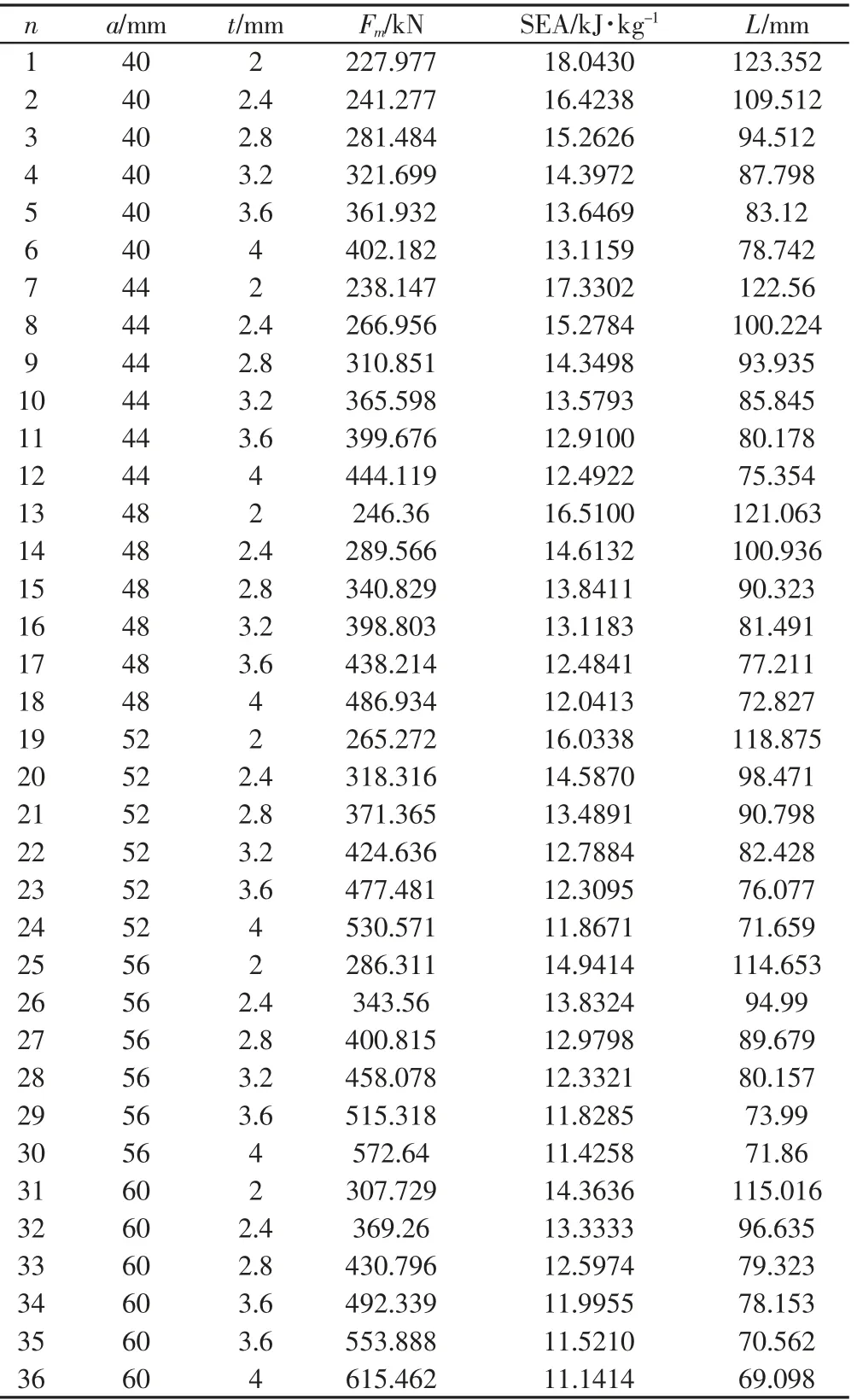
表1 薄壁梁仿真数据Tab.1 Simulation Data of Thin-walled Beam

表2 和平均相对误差值Tab.2 and Average Relative Error Value

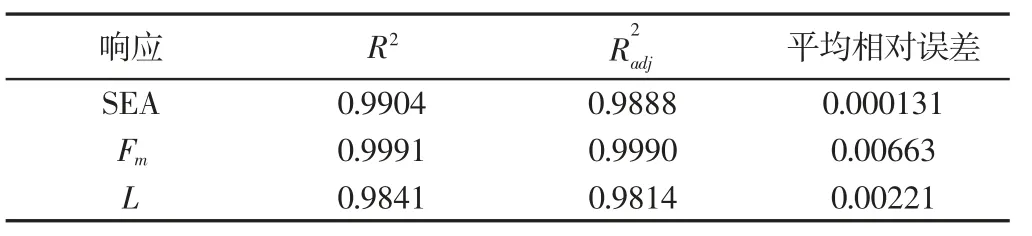
表2 和平均相对误差值Tab.2 and Average Relative Error Value

响应 R2 R2 adj 平均相对误差SEA 0.9904 0.9888 0.000131 Fm 0.9991 0.9990 0.00663 L 0.9841 0.9814 0.00221

采用Matlab 中的优化函数求解式（5）～式（7）函数，得出碰撞过程中薄壁梁的最小比吸能值、最小峰值力以及最小变形量。在根据（1）式中定义的优化问题函数，得到基于比吸能、峰值力与变形量的多目标优化的二阶响应面模型，表达式如（8）式：

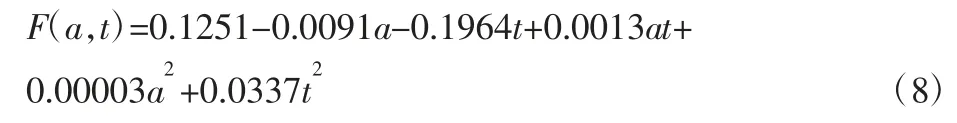
基于Matlab 函数优化，得到最优解为a=40mm，t=2.142mm。用有限元模拟该条件下的碰撞变形，优化模型与设计模型的比吸能、碰撞变形量和碰撞力的比较结果，如表3 所示。从表3 看出。优化后的比吸能虽然减少了4.15%，但最大碰撞峰值减少了5.54%，变形量减少了8.34%，说明优化后的薄壁梁性能有所提高。最优条件下响应面模型的设计值与仿真设计值对比，相对误差都很小，再一次说明了响应面优化方法的有效性，如表4 所示。

表3 优化模型与设计模型比较Tab.3 Comparison Between Optimization Model and Design Model

表4 响应面模型与仿真模型比较Tab.4 Comparison Between Response Surface Model and Simulation Model

4 改进方案分析

材料对薄壁梁的碰撞性能有着很大的影响。针对优化后的模型，用铝合金材料替代结构钢，研究其碰撞性能。铝合金材料参数为：密度ρ=2713kg/m2，弹性模量E=68.948GPa，泊松比ν=0.3，屈服应力为290MPa，应力应变曲线，如图3 所示。

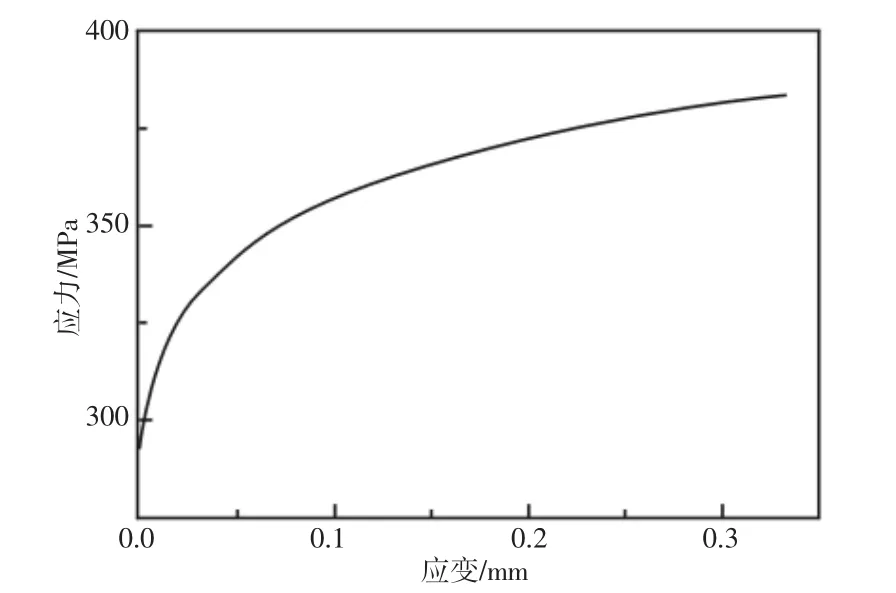
图3 铝合金应力应变曲线Fig.3 Stress-Strain Curve of Aluminum Alloy

建立有限元模型，进行仿真分析，碰撞变形如图4 所示

图4 铝合金材料薄壁梁碰撞变形图Fig.4 Collision Deformation Diagramof Aluminum Alloy Thin-Walled Beam

根据仿真分析的结果，对比吸能、峰值力与变形量进行评价分析，材料替换前后结果的对比，如表5 所示。从中可以看出，铝合金材料的薄壁梁的变形量增加了17.29%，但峰值力减小了36.15%，比吸能增加了109.04%。因此在对生存空间要求不大的情况下，可以选择铝合金材料的薄壁梁结构，降低碰撞力造成的损伤。

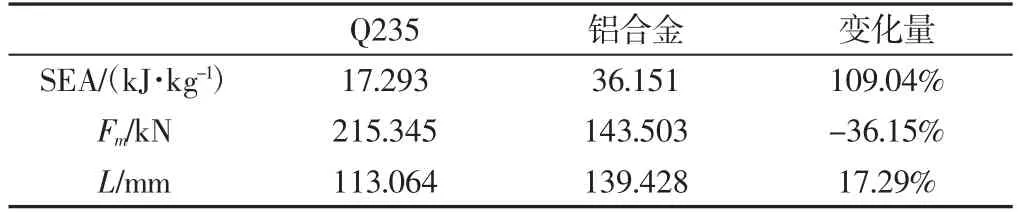
表5 不同材料的对比Tab.5 Comparison of Different Materials

文献[13-14]指出，诱导槽的设置对薄壁梁的碰撞性能影响很大，下面对比研究增加诱导槽与未增加诱导槽的方形薄壁梁的耐撞性能。诱导槽的设置，如图5 所示。截面形状为三角形，槽宽5mm，深3mm，诱导槽左侧距前端10mm，中线间的距离为10mm。碰撞变形，如图6 所示。

图5 诱导槽结构设置Fig.5 Structure Setting of Inducing Grooves

图6 诱导槽结构薄壁梁碰撞变形图Fig.6 Collision Deformation Diagramof Thin-Walled Beam with Inducing Grooves

根据仿真分析的结果，评价结构改进前后的碰撞性能。结构改进前后变形量与峰值力的对比，如表6 所示。从中可以看出，改进后的薄壁梁比吸能增加了2.81%，变形量增加了40.99%，峰值力降低了2.03%。因此增加诱导槽结构对薄壁梁的变形量影响较大，但对于峰值力和比吸能来说影响不大。

表6 不同结构的对比Tab.6 Comparison of Different Structure

5 结论

通过对金属薄壁梁的研究，建立以薄壁梁截面轮廓的几何参数作为设计变量，以薄壁梁在碰撞过程中比吸能最大化、变形量最小化、最大峰值力最小化为目标的多目标优化模型。采用Hyperworks 与ls-dyna 进行联合仿真分析，基于响应面法，利用仿真分析的数据建立函数模型，在Matlab 里面进行优化。优化后的模型比吸减少了4.15%，但最大碰撞峰值减少了5.54%，变形量减少了8.34%。说明优化后的模型性能有了一定的提升。通过响应面值与有限元值的对比分析，也表明了响应面法优化这类问题的有效性。

对于优化后的模型采用材料替代与增加诱导槽结构这两种方法进行改进。替换铝合金材料后的方形薄壁梁比吸能有了显著的提高，同时峰值力也有多降低，但变形量也增加了很多。因此这种薄壁梁适用于对生存空间要求不大的情况，而增加诱导槽结构对综合考虑比吸能、变形量与峰值力的薄壁梁来说效果不好。