短纤维增强复合材料的力学性能仿真研究

张坤伦，潘 锋，2，韩 勇，黄红武

（1.厦门理工学院机械与汽车工程学院，福建 厦门 361024；2.上海迅仿工程技术有限公司，上海201821）

1 引言

随着材料技术的发展，短纤维增强复合材料取得了广泛地应用，如汽车内饰、中控台等[1-3]。短纤维增强材料在注塑成型过程中，由于纤维轴向受注塑方向、纤维长度和模具形状等影响并非完全随机分布，注塑件内部的力学性能呈现明显的各向异性。同时基体树脂中添加的纤维使原材料力学性能，如刚度和强度有所提升。目前短纤维增强复合材料研究主要通过宏观和微观方面研究材料纤维分布及材料的各向异性。文献[4]用哈夫变换等图像处理方法和数值分析相结合获得复合材料的纤维长度及分布信息，从而分析复合材料的微观结构；文献[5]使用扫描电子显微镜观察断面纤维分部情况，清楚地观察到纤维呈束状分布；文献[6]采用LS-DYNA 的22 号正交各项异性材料本构模型，将纤维方向0°、45°、90°力学参数输入，进行玻纤增强仪表板的结构和碰撞分析；文献[7]基于纤维方向0°、30°、45°、60°和90°的样件拉伸试验，研究短玻璃纤维增强PA66 材料的拉伸模量和拉伸强度，并通过对比各相同性模型计算的结果，证明短纤维材料的各向异性参数的计算具有特殊性。短纤维复合材料PP+GF30 具有明显的各向异性、粘弹性和动态应变率效应。仅通过宏观和微观考虑各向异性对其力学性能描述存在不足。

以短纤维复合材料PP+GF30 为例，基于各向异性、粘弹性、动态应变率和断裂失效研究短纤维增强复合材料力学性能。开展不同纤维方向和不同应变率的拉伸试验和断裂失效试验，依据参考文献[6-7]选择研究的纤维方向与注塑方向呈0°、45°、90°，建立其正交各向异性本构模型。采用Hill 1948 屈服准则和韧性断裂失效准则分别拟合出材料的屈服轨迹和平面应力状态下的失效极限曲线。开发表征PP+GF30 力学性能的材料仿真卡片，进行试验与仿真的力与位移曲线对比，研究表征PP+GF30材料力学性能的模拟方法。

2 材料本构模型介绍

2.1 Hill 1948 屈服准则

目前有多种屈服准则描述各向异性材料的屈服轨迹，选择Hill 1948 准则研究PP+GF30 材料的屈服轨迹。平面应力状态下，σx和σy为材料x 轴和y 轴应力，Hill 1948 屈服准则公式：

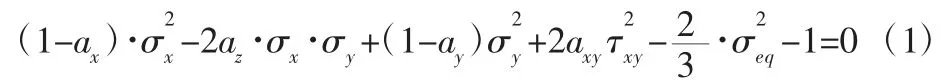
式中：az=1-ax-ay，σeq—单轴拉伸等效应力；τxy—xy 平面的切应力。各向异性参数ax、ay和axy通常由Lankford 系数r0、r45和r90计算求得：

2.2 韧性断裂失效准则

基于CrachFEM 失效理论的正向断裂失效准则[8]，开展PP+GF30 的失效行为的力学性能表征。

在平面应力状态下，通过应力三轴度η 表征单元的应力状态具有唯一性，其表达式为：

式中：p—静水压力；σM—Von Mises 等效应力。

在三维应力状态下，应力三轴度不再是唯一描述单元应力状态的参数，因此在应力三轴度基础上引入主应力比v=σ1/σM，σ1为最大主应力。CrachFEM 失效准则提出了一个全新可以唯一表征三维应力状态的无量纲参数β[9]：

式中：kSF—应力三轴度权重系数，基于三维应力状态参数β 的韧性失效准则为：

3 PP+GF30 材料力学性能表征

3.1 材料弹塑性的力学表征

PP+GF30 存在各向异性。为了综合获得其力学性能应进行不同纤维方向和不同应变率的拉伸试验。拉伸样件切割应远离注塑口，这样纤维排布具有较高的一致性，材料拉伸试验的力与位移曲线，如图1 所示。通过图1（a）可知，不同纤维方向0°、45°和90°所得到力与位移曲线不同，其弹性模量与屈服强度也不同，材料具有明显的各向异性。从图1（b）可知，PP+GF30 具体明显的动态应变率效应，不同应变率会影响材料失效行为。弹性模型是材料的弹性模量。结合图1（a）单轴拉伸试验，拟合PP+GF30 材料应变率0.1/s 时不同纤维方向的弹性模量，如图2 所示。弹性模量在纤维（0～90）°的范围内先减小后增加，纤维0°时弹性模量最大。

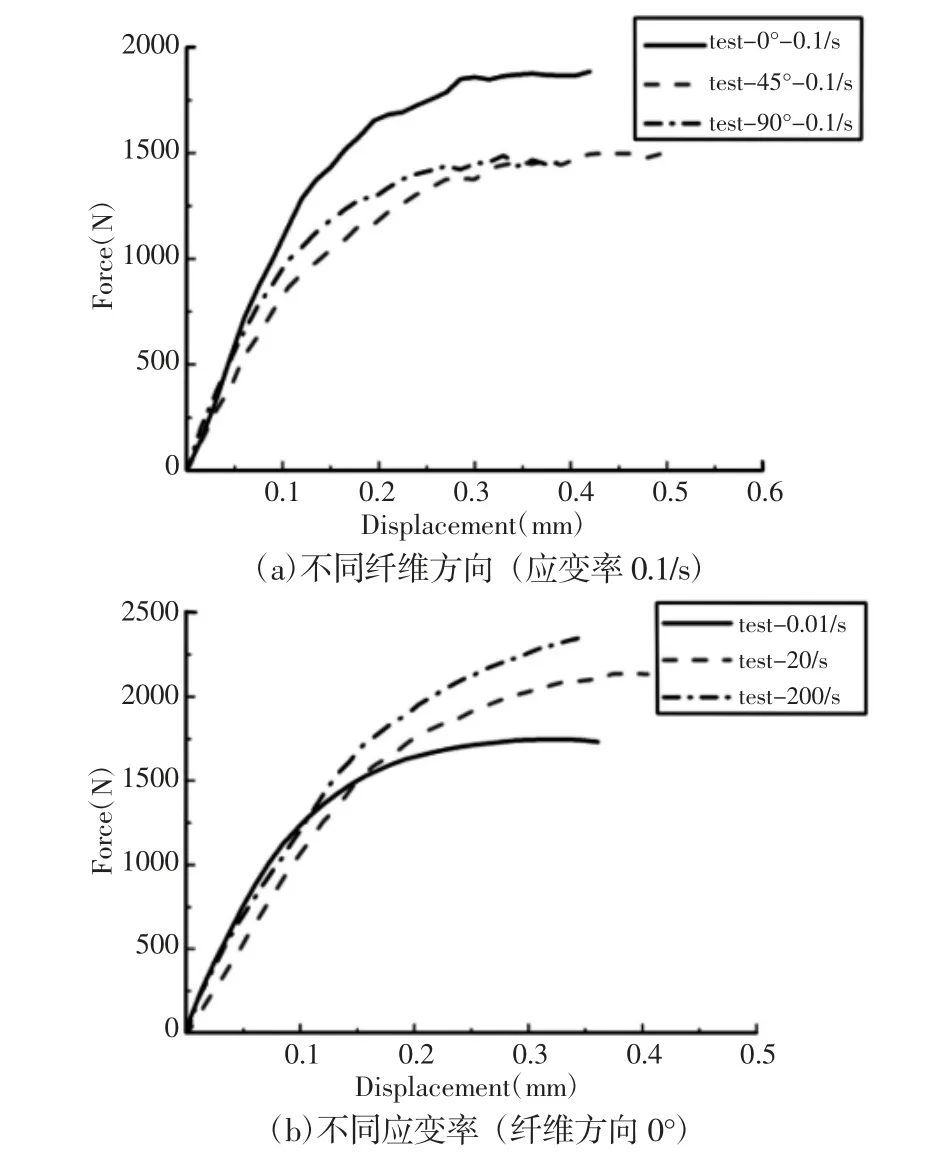
图1 拉伸的力-位移曲线Fig.1 Tensile Force-Displacement Curves

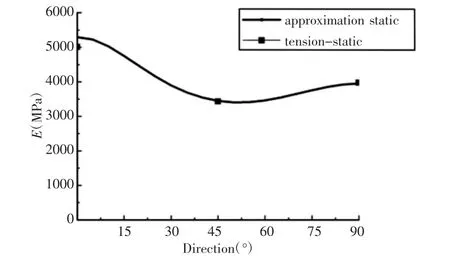
图2 不同纤维方向的弹性模量（应变率0.1/s）Fig.2 Elastic Modulus In Different Fiber Directions（Strain Rate 0.1/s）

塑性模型包括塑性硬化曲线和屈服轨迹。PP+GF30 材料单轴拉伸试验下断裂延伸率为3.9%，需要对塑性段曲线进行拟合外推。PP+GF30 在不同应变率下的硬化曲线，如图3 所示。结合单轴拉伸试验和断裂失效试验，采用Hill 1948 屈服准则拟合材料的屈服轨迹。PP+GF30 材料压缩强度大于拉伸强度，具有拉压不对称性。因此对拟合的屈服轨迹进行修正，以体现压缩强度大于拉伸强度，如图4 所示。

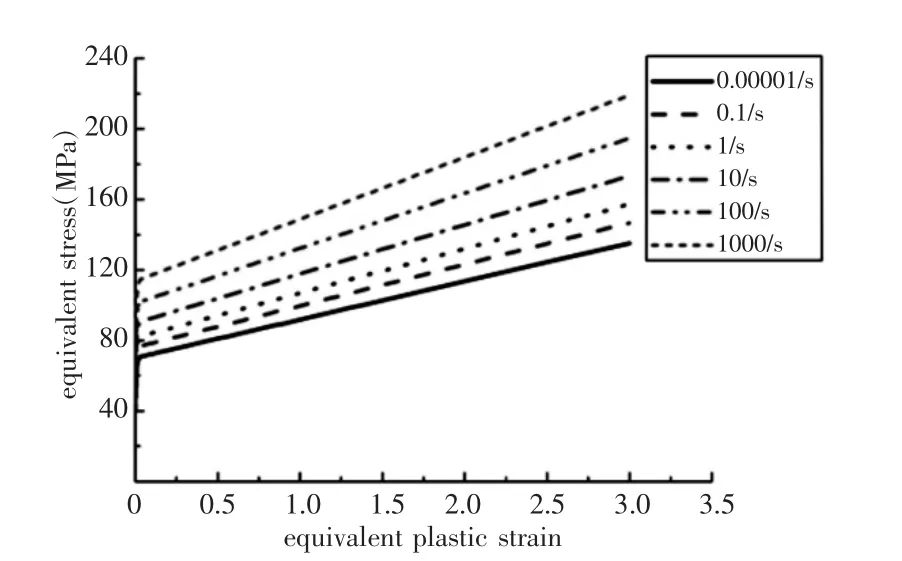
图3 不同应变率硬化曲线（纤维0°）Fig.3 Different Strain Rate Hardening Curves（Fiber Direction 0°）

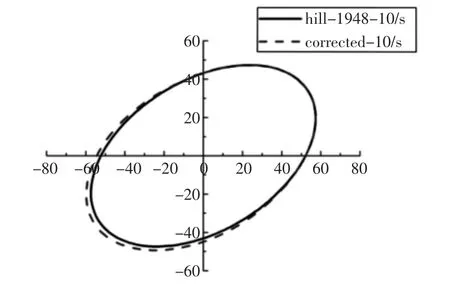
图4 屈服轨迹（应变率10/s）Fig.4 Yield Locus（Strain Rate 10/s）

3.2 材料断裂失效性能的力学表征

PP+GF30 材料断裂失效模型是韧性失效极限曲线。基于典型试验获得材料断裂失效应变，推荐试验矩阵为纤维方向0°、45°、90°三点弯试验[6-7，10]、直角开槽样件拉伸试验和穿孔试验，试验后样件，如图5 所示。

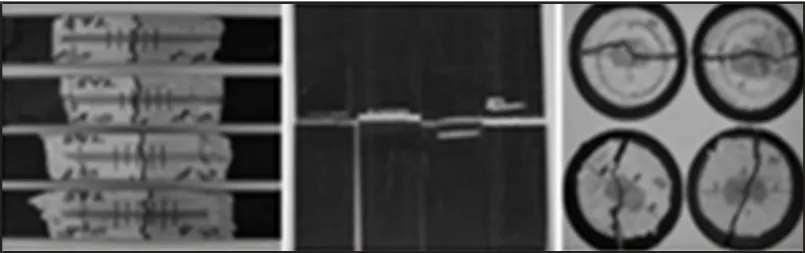
图5 PP+GF30 系统化材料力学试验Fig.5 Systematic Material Mechanics Test Of PP+GF30

通过测量试验前后样件断口区域的厚度和格栅单元尺寸分别求得该应力状态的失效应变值和第二主应变与第一主应变的比值。基于正向断裂失效准则拟合出PP+GF30 材料平面应力状态下的失效极限曲线，如图6 所示。

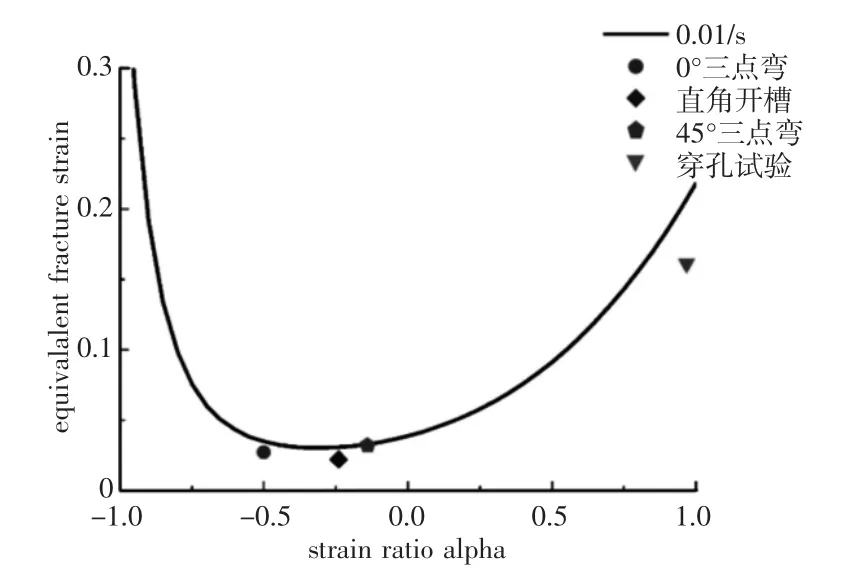
图6 平面应力状态下的失效极限曲线Fig.6 Failure Limit Curve Under Plane Stress State

3.3 材料试验的仿真标定

建立单轴拉伸样件有限元模型，如图7 所示。中间部位网格细化尺寸为1.2mm，为了减少模型计算时间，两端网格尺寸为3mm，设置为刚体[11-12]。分别对PP+GF30 材料不同纤维方向，如图8 所示。不同应变率的单轴拉伸试验进行了力与位移仿真标定，如图9 所示。试验断裂失效应变值和仿真断裂失效应变的对比，材料试验的最大断裂失效应变为5.1%，在计算相对误差时数值显得较小，得到的最大相对误差为11.76%，而试验与仿真应变值相差0.006，两者相差很小，如表1 所示。分析拉伸仿真与试验曲线的吻合度，纤维0°、45°和90°的仿真与试验曲线的相关度分别为99.6%、99.8%和99.6%，应变率为0.01/s、20/s 和200/s 的仿真与试验曲线的相关度分别为99.6%、99.8%和99.6%。Hill 1948 屈服准则和正向断裂失效准则很好地表征PP+GF30 材料的力学性能。

图7 拉伸试验样件Fig.7 Tensile Simulation Model

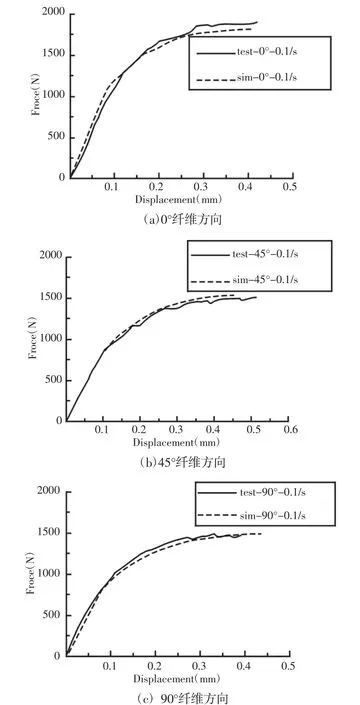
图8 不同纤维方向试验仿真（应变率0.1/s）Fig.8 Simulations of Different Fiber Direction Tests

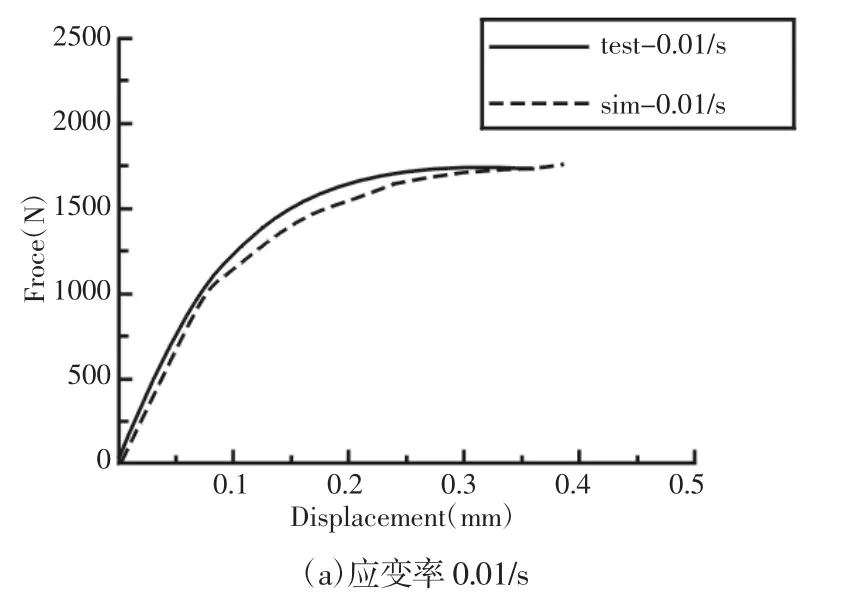
图9 不同应变率试验仿真（纤维00）Fig.9 Simulations of Different Strain Rate Tests

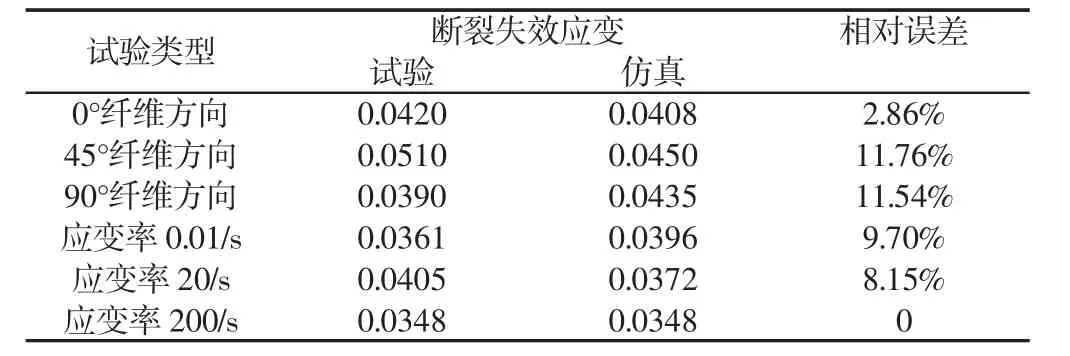
表1 试验与仿真断裂失效应变对比Tab.1 Test And Simulation Fracture Failure Strains Comparison

选择三点弯曲断裂失效试验进一步验证材料卡片的精度，纤维方向为0°和45°。三点弯曲断裂失效仿真模型，样件网格尺寸为1mm。压头、支架及样件两端设置为刚体，如图10 所示。

图10 三点弯仿真模型Fig.10 Three Point Bending Model

仿真与试验曲线对比，如图11 所示。样件在弯曲过程中外侧受拉内侧受压，由外侧向内侧逐步失效，仿真中虽然设置多个积分点，当积分点失效达到一定程度时单元删除，失效模拟存在不足。沿厚度方向建立多层实体单元模拟三点弯曲，会增加模型的计算量，在实际工程中不可取。仿真中断裂失效应变前的纤维0°和45°仿真与试验相关度为99.4%和95.7%，因此PP+GF30 材料卡片是有效的。

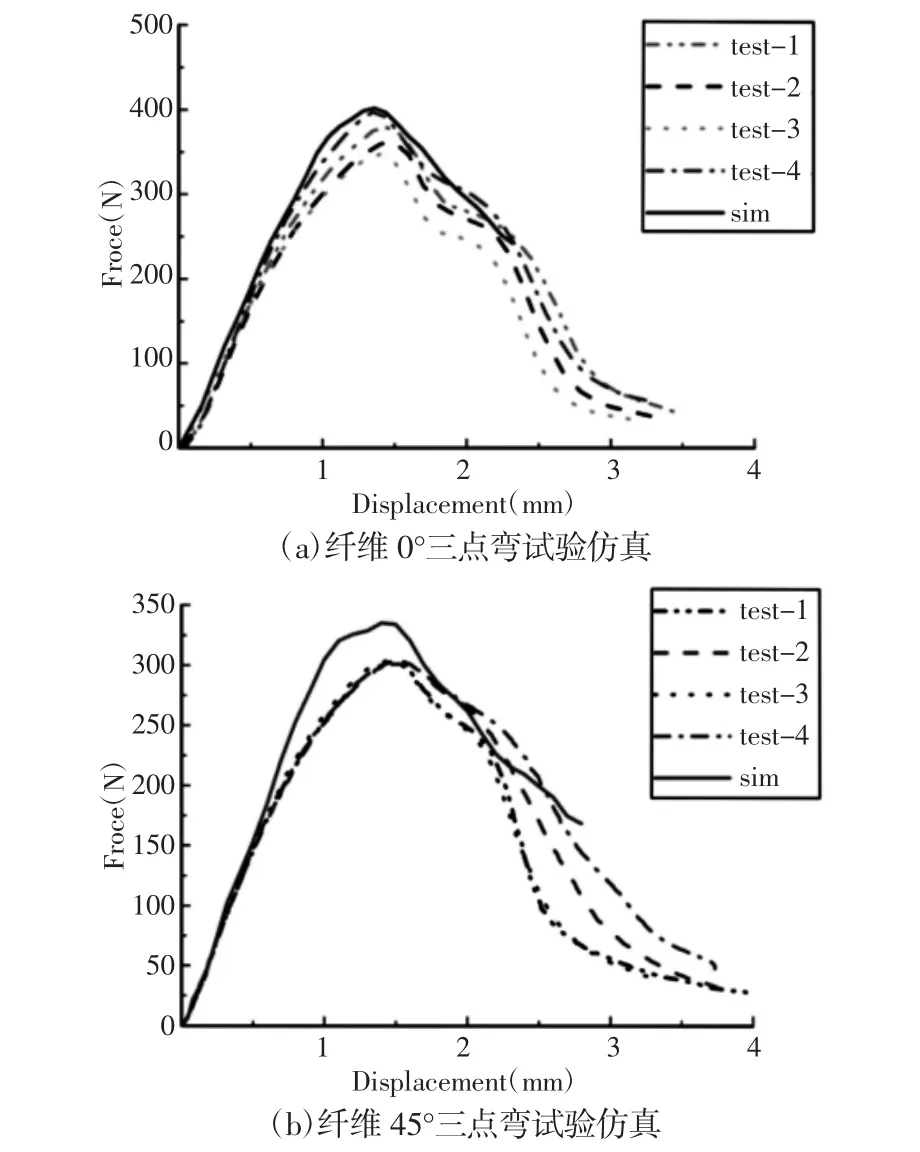
图11 三点弯曲试验仿真Fig.11 Simulations of Three Point Bending Tests

4 总结

为研究短纤维复合材料力学性能有效的模拟方式，开展PP+GF30 有关各向异性、粘弹性、动态应变率和断裂失效的力学试验。采用Hill 1948 准则和韧性断裂失效准则，开发表征PP+GF30 力学性能的材料卡片，进行部分试验的仿真对标。（1）研究不同纤维方向和不同应变率的拉伸试验可知：相同应变率，不同纤维方向的弹性模量不同；相同纤维方向，不同应变率的弹性模量不同。（2）试验与仿真对标结果显示：拉伸试验的断裂失效应变最大相对误差为11.76%，力与位移的相关度最小为99.6%；三点弯曲试验力与位移曲线的相关度最小为95.7%，试验与仿真具有良好的一致性（3）此研究为短纤维增强复合材料的力学性能仿真研究提供了有效的模拟方法。