柔性系统CMAC 神经网络和鲁棒H∞复合控制

付兴建，于士贤

（北京信息科技大学自动化学院，北京100192）

1 引言

1975 年，Albus 提出一种模拟人类小脑结构和功能的小脑模型关节控制器（CMAC-CerebellarModelArticulationController）[1]。人类小脑负责人体运动的协调控制，它可以看作是一种函数，其功能是可以存储和检索产生协调动作的成千上万个肌肉控制信息。小脑模型设计目的就是实现机器人关节的协调控制，其本质是一种基于表格查询技术、局部连接的类感知器的联想记忆网络。现在对小脑模型神经控制的研究主要有两个方面。一是CMAC 神经网络自身性能研究，主要途径是通过与其他算法相结合以改善CMAC 结构、参数和学习能力[2-4]；另一类是针对CMAC 的特点，将其与先进控制策略融合，进行混合控制研究[5-7]。目前，CMAC 在飞行器控制等许多方面得到了广泛应用[8-10]。

柔性机构提出于上世纪80 年代，目前在精密工程、仿生机器人等领域得到了广泛应用。同时由于柔性系统的自身特性，对其控制方式提出了更多的要求，对柔性系统的控制问题进行研究具有一定的理论和实际意义[12-14]。

针对高阶柔性直线系统的跟踪控制，设计了一种将GBFCMAC 神经网络与鲁棒H∞控制相复合的控制策略。首先，将跟踪控制问题转化为标准鲁棒控制，再利用Matlab 中LMI 工具箱求解控制器，然后将鲁棒H∞控制器与CMAC 神经网络复合，构成CMAC 神经网络鲁棒H∞控制。实验结果表明所设计的控制器不仅具有较快响应速度，较短的收敛时间和较好的跟踪精度，而且对于输入端扰动表现出较强的抗干扰能力。

2 高阶柔性直线系统

考虑某高阶柔性控制系统机械结构[15]，如图1 所示。

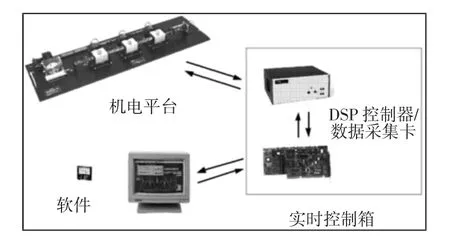
图1 高阶柔性结构系统平台Fig.1 High-order Flexible Structure System Platform

高阶柔性直线系统机电平台的运动部分结构，如图2 所示。

此高阶柔性直线系统状态方程：

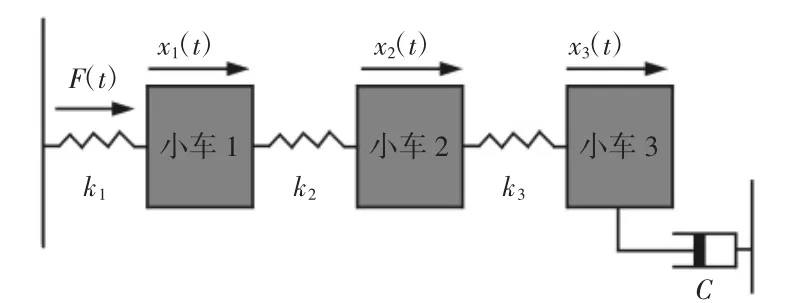
图2 运动部分结构图Fig.2 Motion Structure

加入输入端噪声w 后，状态方程可写为：

设备的参数如下：m1=2.77kg；m2=2.59kg；m3=2.59kg；k1=200N/m；k2=390N/m；k3=390N/m；c=10.2N/（m/s）。

3 鲁棒H∞控制及主要结论

标准H∞控制框图，如图3 所示。图中：w—外部输入信号，包括干扰等；z—输出信号，包括跟踪误差和扰动响应等；y—测量输出；u—控制信号；Δ（s）—不确定项；P（s）—对象；K（s）—控制器。

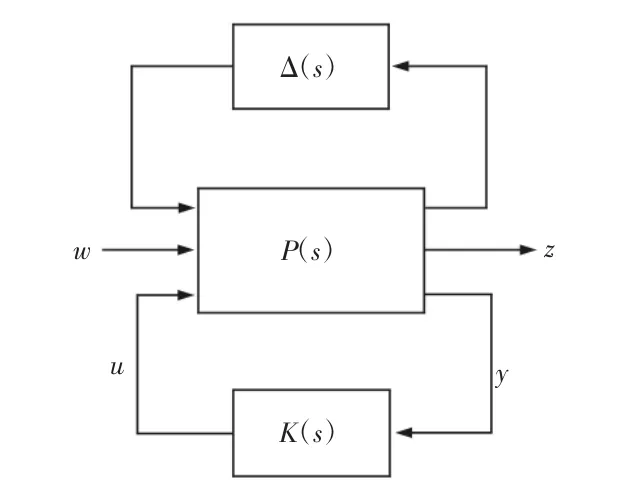
图3 标准H∞问题结构图Fig.3 Standard H∞Control Problem

鲁棒控制的目的就是要在不确定性Δ（s）存在下，针对广义对象P（s），设计控制器K（s），使得信号z 对外部输入w 的响应尽量小。假设广义对象可以化为的形式，如式（3）所示。

标准的H∞的状态方程为：

w 到z 的闭环传递函数矩阵为：

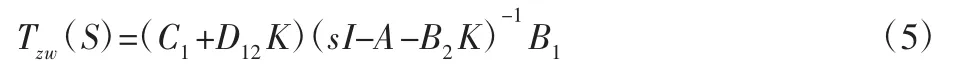
H∞次优控制问题，即求一个控制器u=Kx，使闭环系统内稳定且使‖Tzw（S）‖∞<γ γ≥γ0。

定理对于式（4）所示的线性系统，对于任意γ>0 如果存在对称正定矩阵X 和Y，使得式（6）成立，则控制器u=Kx=YX-1x 使系统渐近稳定且‖Tzw（S）‖∞<γ。

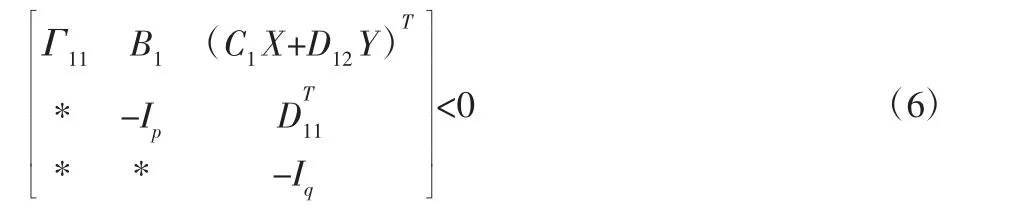
其中，Γ11=AX+B2Y+（AX+B2Y）T，*—对称转置。证明：略，可参考文献[14]。

4 CMAC 神经网络

由于CMAC 神经网络具有局部连接、收敛速度快和逼近精度高等优点，在控制领域（尤其是机器人控制系统中）得到广泛应用，CMAC 神经网络的算法也得到了多种方式的改进[12]。其中，Chiang 和Lin 将Albus 提出的CMAC 的常数型基函数推广到了一般类型的基函数，并引入了可微型基函数，使CMAC 具备了记忆微分信息的能力，如引入高斯基函数的GBF-CMAC（Gaussian Base function CMAC）即为其中一种。GBF-CMAC 神经网络映射原理，如图4 所示。

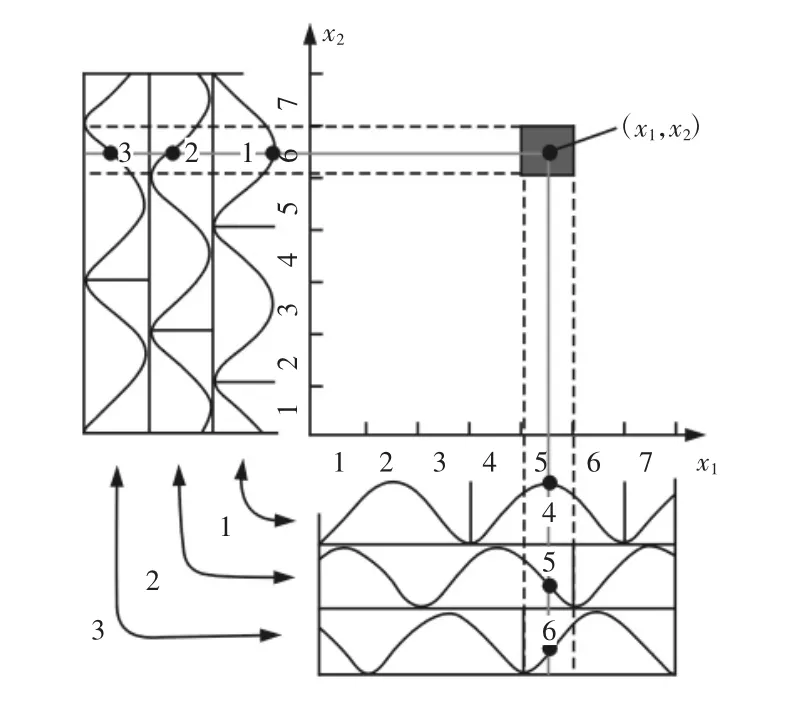
图4 GBF-CMAC 映射原理Fig.4 GBF-CMAC Mapping Principle

GBF-CMAC 在传统CMAC 映射中，增加一个基函数。基函数矩阵是对角矩阵，其对角线元素中有Ne个非零值，位置为pj，j=1，2，…，Ne计算，如式（7）所示。

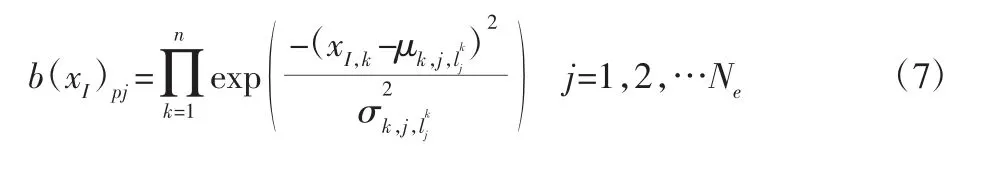
式中：xI，k—输入向量的第k 维—输入向量第k 维对应的第j 层第个分块的高斯函数的中心和宽度。

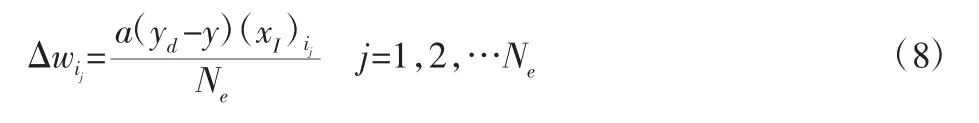
式中：ij∈｛1，2，…Nh|a（xs）相应位置为1｝，α∈（0，1）—学习率，其余权值不更新。

5 基于CMAC 神经网络的鲁棒H∞控制

针对高阶柔性直线系统，基于GBF-CMAC 神经网络的鲁棒H∞跟踪控制器结构，如图5 所示。控制器，如式（9）所示。

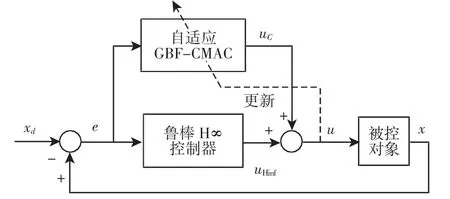
图5 复合跟踪控制系统结构图Fig.5 Compound Tracking Control System Structure

根据图5 和式（9）分析所设计的跟踪控制系统可知，初始阶段总控制输出主要为鲁棒控制器的输出uH∞（t），此时神经网络控制器处于学习阶段；随着神经网络的不断学习，总控制输出将主要由神经网络控制器提供，此时鲁棒控制器的主要作用是保证系统的稳定性。控制参数取时间T=5s，步长ΔT=0.003s。高阶柔性系统状态期望值为阶跃信号。输入端加入高斯白噪声作为干扰信号，由Simulink 的Band-Limited White Noise 模块产生。

CMAC 部分利用符号函数式将6 维输入变成3 维输入，结构参数和学习参数设置为Ne=5、Nb=3，22 和42、α=0.005 和U=3。

基于CMAC 神经网络，将文中定理得到的控制器与最优二次型控制器LQR 进行比较，令性能指标为dt，取Q=CTC，R=1，C=［0 0.02 0 0 1 0］T。利用Matlab 的LQR 函数工具，计算得到状态反馈控制向量为：

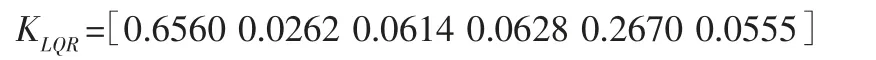
求解式（6）得鲁棒H∞控制器为：

在没有噪声和加入白噪声情况下，考查柔性运动结构中小车3 的位置跟踪效果，其误差曲线，如图6 所示。图6（a）是没有加入噪声干扰情况，可以看出所设计的复合跟踪控制器与传统最优二次型控制器相比，具有更快的响应速度和更短的收敛时间。加入白噪声干扰时，比如白噪声功率谱密度（Power spectrum density，PSD）值分别为0.1 和1 时，从图6（b）和图6（c）可以看出，传统的最优二次型控制器有振荡现象，且噪声越大震荡越剧烈，而设计的CMAC 神经网络和鲁棒控制相结合的复合控制在一定强度干扰下，控制效果几乎不受影响，表现出较强的抗干扰能力。

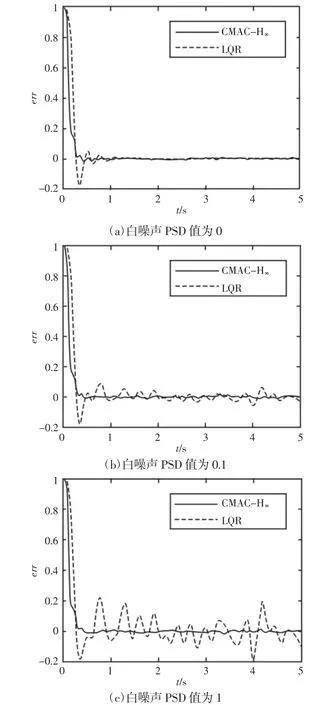
图6 跟踪误差曲线Fig.6 Tracking Error Curves

6 结语

针对具有高阶柔性机械结构系统，设计了将GBF-CMAC 神经网络与鲁棒H∞控制相融合的控制策略。通过将跟踪控制问题转化为标准的鲁棒控制问题，可利用Matlab 中的LMI 工具箱求解控制器参数。实验结果表明所设计的控制器不仅具有较快的响应速度，较短的收敛时间和较好的跟踪精度，而且对于输入端扰动表现出较强的抗干扰能力。