引领学生“深度学习”的教学之道
□陈华忠
《义务教育数学课程标准(2011年版)》指出:“作为促进学生全面发展教育的重要组成部分,数学教育既要使学生掌握现代生活和学习中所需要的数学知识与技能,更要发挥数学在培养人的思维能力和创新能力方面的不可替代的作用。”为此,教学应遵循数学学科特点、遵循学生成长规律,引导学生大胆猜测、深入思考,引领学生深度学习。
一、以问题为驱动,打开深度思考之门
数学家哈尔莫斯说过:“问题是数学的心脏。”教学中,教师要以问题为导向,引导学生独立思考、自主探究、合作交流,打开学生深度思考之门。例如,在教学“平行四边形的面积”一课时,教师以“帮助工人计算草坪面积”为情境,提出:“这块平行四边形草坪的面积如何计算?”让学生猜一猜,鼓励学生思考不同的方法,并进行自主验证,以“为什么平行四边形面积等于底乘高”引导学生深入思考,促进学生自主探究。平行四边形面积计算的教学,不仅要让学生知道平行四边形的面积如何计算,而且要让学生知道为什么平行四边形的面积等于底乘高。通过问题引领,学生对平行四边形面积的计算公式的推导过程有了深刻的理解与思考,从而促进学生进行深度学习。
又如,在教学“三角形的分类”一课时,本课的主要问题是“分类的标准是什么”“为什么这样分类”。教师引领学生通过操作、比较、观察、感悟,发现三角形只要具有“共同的特征”就可以归为一类。这样就很清楚地解释了为什么“一直二锐”与“一钝二锐”不能合为一类,正是因为它们“共同的特征”不一样,所以分成三类。
二、以互动为途径,开展深度交流之话
交流互动的课堂最具魅力,教师在教学中应摒弃“师问生答”的传统方式,更多地使用“生生互动”的方式,让学生在交流互动中,相互启发、相互碰撞,弄清问题的本质。
例如,在教学“9的乘法口诀”时,教师引导学生观察算式并思考:“从上往下看,这些算式有什么变化?”“再从下往上看,这些算式又有什么变化?”“你发现了什么?”等。学生自由表达自己的想法,而教师可以根据学生的表达,发现学生思维的不足,及时地给予点拨引导,促进学生思维的发展。又如,教学“商不变的性质”时,学生经过观察得出“被除数和除数同时扩大或同时缩小相同倍数,商不变”这一性质。此时,教师出示6÷3=(6×0)÷(2×0)=3让学生判断正误。学生就能够发现2×0=0,但是0不可以作为除数。可见,刚才得出的性质不够准确、不够完整,应该在条件中补充“扩大或缩小的倍数不能为0”。面对学生的发言,教师应该耐心等待,适时引导、辨析,直至学生深刻理解商不变的性质。
三、以活动为载体,做实深度体验之功
数学的活动经验需要在“做”的过程和“思考”的过程中积淀。只有让学生亲身体验数学知识形成与发展的过程,才有真正的深度体验。
例如,教学“涂色正方体表面积”时,教师首先展示了一个由27个小正方体拼成的涂色大正方体,然后让学生打乱这个大正方体,看谁能花最短的时间还原。学生发现拼不出来后,教师问:“难在哪里?”学生说不知道哪个小正方体具体在什么位置。接着教师点拨引导,学生进行探究,发现了涂色正方体的特点,学生思维受到了启发。教师又让学生拼一拼由64个、81个小正方体拼成的涂色大正方体,这一次有好几组学生很快就拼出来了。教师打破以往观察涂色正方体、寻找涂色规律的教学方式,把涂色的大正方体打乱,让学生还原,培养了学生的空间观念,提升了学生的数学素养。
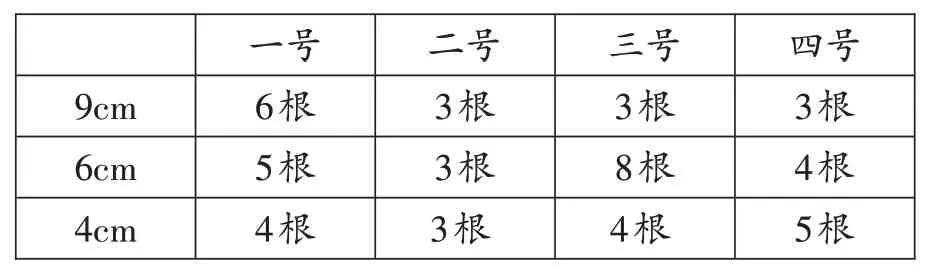
又如,教学“长方体的认识”时,教师组织学生小组内动手操作,并讨论交流:第几号材料可以搭出长方体框架?
?
小组成员相互探讨,不断尝试,在实验、分析、思考中发现:(1)如果是三组不同长度的小棒,每一组至少要有4根;(2)如果是两组不同长度的小棒,有一组至少要有8根小棒,一组至少要有4根。学生深度参与,积极体验,真正验证了“自我发现的东西能积极地同化,从而产生深刻的理解”这一理念,深化了对长方体棱特征的认知,提升了学生的思维能力。
四、以方法为手段,体验深度探究之旅
深度学习不是一个接受知识的过程,而是发现、探究与创造的过程。如何引导学生自己去发现、去探究,体验知识的形成过程,尝到成功的愉悦呢?笔者认为,很重要的一点是多提供给学生自主探究的时间与空间,做到凡是学生自己能独立思考的,教师绝不提示,凡是学生自己能探究的,教师绝不替代。例如,在教学“圆的认识”时,在“探索直径和半径的特点”这一环节,教师放手让学生进行自主探究。
1.小组探究。以小组为单位,利用圆片,采用画一画、量一量、折一折等方法进行探索和研究:(1)半径有多少条?直径呢?(2)半径有什么特征?直径呢?(3)半径与直径之间的关系是怎样的?
2.交流汇报。学生通过折、画、量等实践活动,发现圆半径与直径的特征、半径与直径的关系,从而体验知识的探究过程,感受成功的喜悦。

