化静为动，发展空间观念——以“图形与几何”领域的教学为例

□曹冠军

皮亚杰的研究表明：静态表象只能产生物理经验，动态表象是学习数理——逻辑经验生成的源泉。让静止的图形动起来，化抽象为直观，有利于学生直观洞察、分析推理、发现本质，对图形形成深刻表象，进而深化转化思想，构建知识体系，培养学生化静为动的思维方式。

一、动态展示形成过程，形成深刻表象

教师通过动态展示，运用平移、旋转、轴对称等几何变换方法，可以直观地呈现图形变化、形成的过程，引导学生沟通和感受图形之间的关系，形成深刻表象，促进对图形的本质理解，完善知识结构，发展空间观念。

如“柱体的体积”教学中，要计算立体图形（如右图）的体积，学生可能会运用不同的方法：

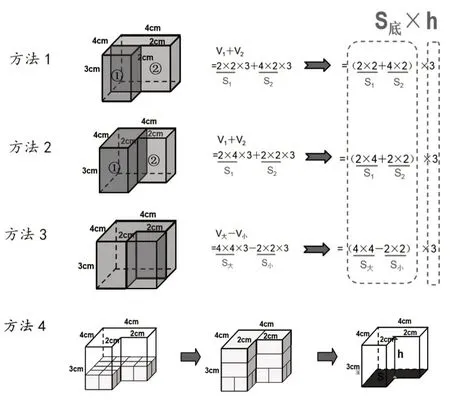
方法1—方法3，运用的是“割补法”，方法4则是通过单位立方体的层层“累加”得出结果。通过沟通不同方法间的联系，学生体会到如果每一层的体积单位相同，那么不规则的立体图形也可以是一层一层体积单位的累加，用底面积×高的方法计算，立体图形在叠加中动了起来，学生更加深刻地理解，在求不规则柱体体积时可运用不同的转化方法，让数学学习温故而知新。

之后教师还可以通过这样的题目进一步引导学生对不规则立体图形进行正反辨析，以完善和深化学生对柱体概念本质的理解，形成深刻的表象。

下列哪些图形的体积可以用“V=Sh”来计算。

通过找到底面的体积单位，引导学生观察是否可以一层一层地累加上去，在平移过程中图形的形状、大小不变。尤其是图形⑥和图形⑦的展示，进一步丰富了柱体概念，拓宽了学生的视野。

二、动态剖析变化瞬间，深化转化思想

教师在教学中应给学生提供丰富的“动态素材”，让学生通过动手实践，直接感知图形的特点，体验图形的变化过程，引导学生通过操作与想象相结合的方式去观察与思考问题，从而积累丰富的活动经验，深化转化思想，进而对图形有更深刻的认识和感受，发展空间观念。

如在“三角形等积变形”的教学中，教师呈现学习任务：以BC为底，画出与△ABC面积相等的三角形（如右图）。请独立完成，并清楚地表示出三角形的高。

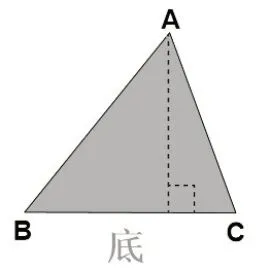
交流反馈：

师：比较这三种方法，哪种更简洁？生：添上两条平行线的方法3。

师：为什么添上平行线更加简洁？生：不需要量高，高都一样长。

生：这些高就是两条平行线之间的距离。

师小结：刚才量高的方法，如果量得准确一点，得到的这些三角形的顶点都会在上面这条平行线上，并且这些三角形的高就是两条平行线之间的距离。

师：BC底不动，现在把三角形的顶点A向左移动，它会是一个什么三角形？（锐角三角形，直角三角形，钝角三角形）

师：把顶点A向右移动。像这样的三角形可以画多少个？

师：在三角形的顶点移动的过程中，你发现了什么？

师小结：我们把这些三角形叫作等底等高的三角形，等底等高的三角形面积相等。在两条平行线之间，如果三角形的底相同，我们只要移动底对应的顶点，就可以画出无数个等底等高面积相等的三角形。

在教学中，激活、利用与提升学生已有的经验非常重要。教师引导学生展开自主探究，并通过有层次的展示交流，帮助学生发现这些三角形的顶点都在上面一条平行线上，三角形的高就是两条平行线之间的距离，从而引出平行线中底不动、顶点移动的过程。化静为动，学生在比较中感知、内化等底等高的三角形模型的表象，为三角形的等积变形做铺垫。

这一素材还可以再次被利用，让学生的思维得到延续。

呈现要求：画出与这两个三角形面积之和相等的一个大三角形。

交流反馈：

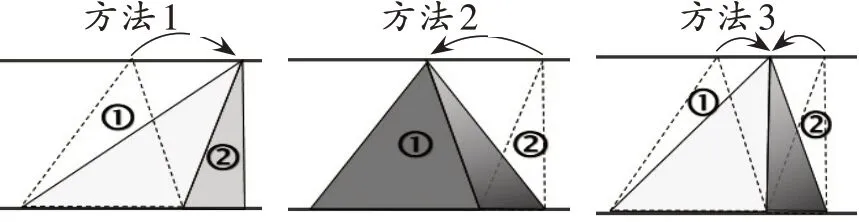
生：方法1中，①号图形的顶点移动到和②号的顶点重合，①号图形与移动后的图形同底等高面积相等，所以①和②的面积之和就是图中阴影部分三角形的面积。

师：在这个转化过程中，谁动了，谁没动？

生：①号动了，②号没动。

……

师：刚才这两种方法有什么共同点？

生：只动了一个三角形。

师：但是在转化过程中，这条底始终不动。

生：方法3中，①号②号的顶点都移动到中间某一点，移动后左边三角形和①号图形同底等高，右边三角形与②号图形同底等高。因此阴影中三角形的面积就是原来①号和②号的面积之和。

师：现在①号图形和②号图形都动了，但其中什么跟前面一样一直都没动？

生：底边没动。

师小结：三角形转化成与它等底等高面积相等的三角形，这样的转化叫作三角形的等积变形。这三种方法都有一个共同点：这条底边始终不动。两条平行线之间，三角形等积变形的过程中，它们的顶点在移动，最后顶点重合在一起，组成了一个大三角形。在此基础上学生还感受到，只要以两个图形的底的和为底，上顶点沿着上面这条平行线任意移动，得到的所有三角形的面积都是原来两个三角形面积的和。这里把前面环节中内化的模型表象外显出来，以此进一步深化表象，学生更深刻地理解三角形等积变形的本质，思维在图形运动的过程中更加灵活。

三、动态沟通转换关系，构建知识体系

动静结合的想象，少一些直观演示，多一些空间想象，引导学生在脑海中对图形进行提取、改造、重组，建立空间表象，动态沟通图形间的关系，有效建构知识体系，使学生形成完整的数学思维体系，发展空间观念。

如“圆锥的拓展练习”教学中，教师提出以下问题：如果直角△ABC的顶点A沿着中间这条平行线向右移动1.8cm（或向左移动1.2cm），它变成了一个什么三角形，绕BC旋转后的体积是多少？

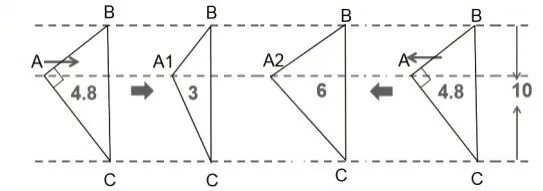
师：三种不同类型的三角形绕BC旋转一周，在求所形成的图形体积的过程中，有什么相同之处？

生：都可以把顶点到旋转轴的距离作为圆锥的底面半径，旋转的那条边作为高，转化成一个大圆锥来求体积。

师：如果三角形的顶点沿着平行线的垂线向下移动到A1，并绕BC旋转一周的体积是多少？

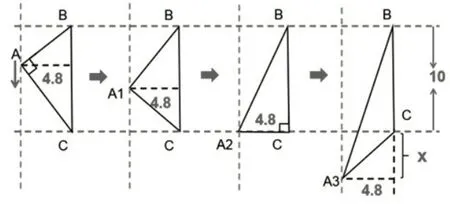
生：都可以转化成底面半径是4.8，高是10的圆锥，体积不变。

师：如果继续往下移动到A3，体积还会不变吗？

生：这个图形的体积是大圆锥的体积减去小圆锥的体积：7.68π×（10+x）-7.68πx=76.8π。体积还是不变。

师：三角形顶点A移动的过程中，你发现了什么？

生：体积始终不变。体积与BC的长度和BC边上的高有关。

生：我们都可以把它们转化成以BC边上的高为底，BC为高的一个圆锥来求体积。

顶点A在横向、纵向移动的过程中，通过观察、比较不同类型的三角形分别绕BC旋转一周后图形的体积，沟通方法间的共性，经历具体到抽象的概括过程，引导学生对方法进行总结和归一：把顶点到旋转轴的距离作为圆锥的底面半径，旋转的那条边作为圆锥的高，最后求圆锥的体积。

之后还可以继续呈现任务：如图，两组平行线互相垂直，△ABC的两条边正好在两组平行线上，如果△ABC的顶点C向下移动，并绕L2旋转一周，所形成的图形的体积是多少？

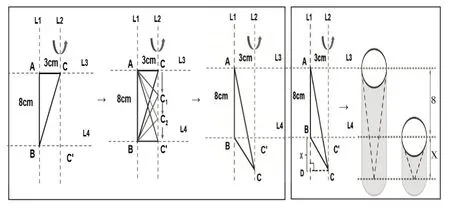
生：我们可以这样想，这相当于圆柱里面削去了两个等底的小圆锥，也就是相当于削去了一个与圆柱等底等高的圆锥，剩下的部分就是圆柱体积的

师：如果顶点C继续往下移动呢？图形的体积还会不变吗？如果顶点C向下移动x厘米，图形旋转后的体积是多少？生：图形的体积是大圆柱体积的减去小圆柱体积的6π×（8+x-x）=48π。体积始终不变。

顶点C移动到C'的过程中，引导学生逆向思考，深刻认识图形的体积始终是圆柱体积的，继续深入探究，如果C继续下移，通过计算发现C在L2上移动的过程中，体积始终不变，有效地沟通了三角形沿边、沿顶点旋转后图形间的关系，构建知识体系。

综上所述，化静为动，让学生学会“动态地想”，能“动态地想”，不断创设让静止的图形动起来的机会，为学生创设想象的空间，可以有效提升学生的思维品质，发展空间观念。