高中数学立体几何教学措施分析

林志强

摘  要：在新课程教育改革背景下，高中数学立体几何教学中，教师应采用多种教学方法，让学生通过在多种教学方法中，理解和掌握高中立体几何学习的重点，从而提高学生的学习效率。本文围绕高中数学立体几何教学实施的措施展开讨论，为高中数学立体几何教学提供参考依据。

关键词：高中数学;立体几何;教学探索

引言：

高中数学中，立体几何是重要的组成部分，但是立体几何知识难点较多，教师采用传统的教学方法，不利于学生理解和掌握立体几何知识。教师应以培养学生空间想象能力为目标，结合教学内容，综合考虑学生的学习能力以及逻辑思维，为学生设置合适的学习内容，通过应用典型结论、转化思想以及立体模型等，使学生消除学习中遇到的难点，有助于学生获得良好的学习效果。

1.培养学生空间想象能力

教师在讲解立体几何知识时，应给予培养学生空间想象能力足够的重视。教师使用多种立体几何模型，让学生认真观察模型在空间中的特点，使学生在脑海中形成立体几何图形，有助于学生在解答立体几何问题时，会在脑海中快速勾勒出立体几何图形，在图形中设置必要的解题条件，合理利用条件解决立体几何问题。教师在培养学生立体几何空间想象能力时，应遵循由简至繁的原则，使用立方体、长方体等基础立体几何模型，让学生掌握立体几何的长、宽、高、面对角线以及棱对角线等知识点，有助于增强学生对立体几何图形在空间中的理解能力。

例如，在讲解数学《立体图形的直观图》知识时，本节知识的教学目标，要求学生学生会画出常见的几何体，直棱柱、圆柱、圆锥以及球的直观图。能够分析一些组合体的结构特征，掌握一些简单组合体的画法;培养学生直观想象和几何作图能力。学生在学习期间，观察立体图形的直观图，可以有效培养学生空间想象能力，使学生掌握正方形的判定方法。

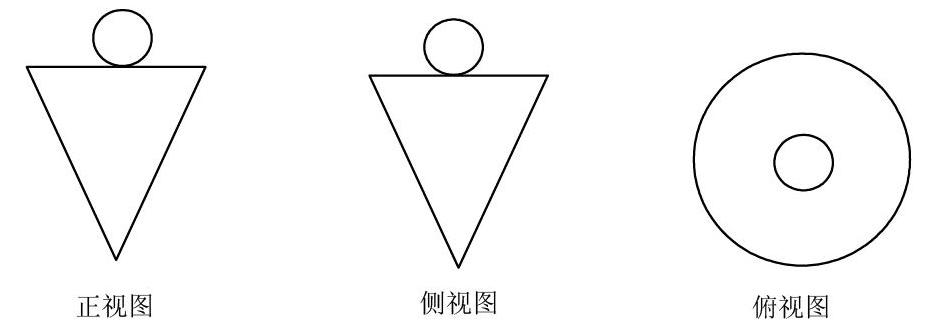
例如习题如图所示，所给出的一个几何体的三视图，那么画出这个图形。学生通过空间现象力，可画出该几何图形。

2.立足课本，强化学生的基础能力

教师在讲解高中数学立体几何知识时，应立足课本内容，指导学生做好基础知识的学习，学生做好基础知识学习，有助于学生不断提高学习质量。根据新课程教育改革要求，高中教师在立体几何知识时，应为学生制定适合的学习内容，让学生在学习立体几何知识时，可以理解和掌握立体几何知识，并且通过练习，可以提升学生的应用能力，有助于学生获得良好的学习效果。

例如，在讲解数学《简单几何体的表面积与体积》知识时，本节教学目标要求学生掌握了解柱、锥、台的表面积计算公式，能运用柱锥台的表面积公式进行计算和解决有关实际问题。使其掌握基础知识，如理解计算公式的由来，运用公式解决问题。教师应立足课本内容，强化学生掌握简单几何体的表面积与体积的基础知识。

3.总结规律，规范训练

在高中立体几何知识教学过程中，教师应组织学生进行立体几何知识专项训练，通过专项训练总结规律，进一步规范学生的训练方法。学生在专项训练过程中，教师应充分引导作用，与学生进行有效的交流，通过交流帮助学生总结立体几何知识的规律，使学生在训练中规范操作方法，并提升学生应用规律的能力，从而帮助学生获得良好的训练效果。

4.典型结论的应用

高中立体几何教学中，教师应灵活应用典型结论，将已经应用较为广泛的结论，用于解决学生解题时遇到的问题。高中立体几何知识具有一定的复杂性特点，在许多题型中，学生应掌握典型结论的应用方法，以便帮助学生找到解题思路，然后学生应用正确的方法，可以顺利的解答问题。

例如，在讲解数学《空间点、直线、平面之间的位置关系》知识时，本节教学目标要求学生理解空间点、直线、平面之间的位置关系，并能空间点、直线、平面之间的位置关系问题。教师应向学生重点讲解空间点、直线、平面之间的位置关系。会判断空间中直线不直线间得位置关系、直线不平面、平面不平面间得位置关系。应用典型结论解决该问题。学生在应用三个公理解决问题时，会培养学生的分析问题、解决问题的能力，并且培养学生综合运用知识的能力，帮助学生养成良好的学习习惯。

例1：已经平面点击并拖拽以移动//平面点击并拖拽以移动，直线l点击并拖拽以移动点击并拖拽以移动，点P点击并拖拽以移动直线l，平面点击并拖拽以移动、点击并拖拽以移动间距为8，则点击并拖拽以移动内到点P距离为10，那么到l的距离为9的点轨迹为

A.一个圆

B.两条直线

C.四个点

D.两个点

此题较为简单，如果学生对点线距离、面面距离及线线距离关系掌握不佳，就可能出现错误，在教学中，教师通过强化学生典型结论应用意义，可以让学生做出正确选择。

5.转化思想的应用

轉化思想是高中立体几何教学中应用较为广泛的思想，在立体几何问题中，需要学生通过转换条件，在问题中设置多种解题条件，学生根据条件可以快速解答出立体几何问题。在转化思想应用时，学生还应掌握数形结合思想，或者分类讨论思想，学生配合使用不同的思想，可以快速找出解决问题的方法。

例如，在讲解数学《空间直线、平面的垂直》知识时，本节教学目标要求学生了解圆与点之间的位置关系，掌握应用数量关系，使学生加深对空间直线、平面垂直知识的整体认识，对解决空间中的垂直问题形成策略和方法，掌握解决问题的通性通法，培养学生自身的思考与总结能力。

结语：

综上所述，在高中数学立体几何教学过程中，教师应重视学生基础知识的训练，通过提升学生的基础知识应用能力，逐步运用其他教学方法，一方面有效培养学生的空间想象能力，另一方面使学生可以深刻理解和掌握立体几何知识，学生在应用立体几何知识时，可以提高解决立体几何问题的效率，促进学生立体几何素养快速发展，为今后学生学习立体几何知识奠定坚实的基础。

参考文献

[1]  金波.高中数学立体几何教学探究[J]中学生数理化（教与学）. 2018（02）：87.

[2]  许程媛. 高中数学课堂中立体几何的教学策略研究[J]新课程（中学）. 2017（11）：464.