低速冲击激励下嵌入黏弹性阻尼芯层的纤维金属混杂层合板动态响应预测模型1)
李则霖 李 晖,,2) 王东升 任朝晖 祖旭东 周 晋 官忠伟 王相平
∗(东北大学机械工程与自动化学院,沈阳110819)
†(东北大学航空动力装备振动及控制教育部重点实验室,沈阳110819)
∗∗(中国航发沈阳发动机研究所,沈阳 110015)
††(利物浦大学工程学院,英国利物浦L693GQ)
∗∗∗(南京理工大学机械工程学院,南京 210094)
†††(西安交通大学机械工程学院,西安 710054)
引言
纤维金属层合板(fiber metal laminated plates,FMLPs)是一种由金属和纤维增强复合材料组成的混杂复合材料板,具有轻质、高强、阻燃、耐冲击、抗疲劳等诸多优点[1-3],已逐步在航空、航天、轨道交通、兵器工业等领域得到应用[4-8].目前,FMLPs的抗低速冲击动力学性能研究一直备受关注.
在20 世纪90 年代,荷兰学者Vlot[9]就对FMLPs 的冲击特性进行了研究,并第一个建立了该类型层合结构的冲击解析模型.之后,Vlot 研究团队[10-12]对分析方法不断完善,深入研究了低速、高速冲击激励下的动态力、位移响应、损伤面积、裂纹长度等问题.Davies 等[13]建立了FMLPs的有限元模型,并预测了冲击激励下结构的动响应和动应变.Payeganeh 等[14]通过两自由度弹簧--质量系统,建立了FMLPs 在低速冲击激励下的解析模型,并分析了不同冲击速度对冲击接触力、响应等参数的影响.傅衣铭等[15-16]基于多种失效准则,综合运用正交配点法、Newmark 法和迭代法对复合材料板壳的冲击动态响应进行求解.Starikov[17]对不同材料组成的FMLPs 进行了一系列低速冲击试验,推导获得了层合板结构、性能与压痕冲击响应之间的关系.陈勇[18]基于Hashin 失效准则建立了冲击载荷下FMLPs 的二维和三维损伤模型,预测了结构的损伤行为及动态响应,并通过落锤实验进行了模型验证.Jones[19]采用刚性与塑性材料近似法,对FMLPs 的实际横截面进行了修正,得到了简单的计算公式来预估低速冲击后结构的最大永久横向位移.
黏弹性材料可有效地提升结构阻尼性能[20-21],若能够将该类型材料填充到纤维金属层合板中,则可极大地提升FMLPs 的抗冲击性、耐疲劳性及服役可靠性.然而,目前对嵌入黏弹性芯层(viscoelastic core,VC)的FMLPs 结构(简称为VC-FMLPs)冲击特性的研究报道很少,仅有零星文献对嵌入黏弹性芯层的三明治结构的低速冲击问题进行了初步的研究.例如Malekzadeh 等[22]提出了一种改进的动态高阶冲击理论,并求解获得了嵌入软芯层的三明治结构的低速冲击响应,但是该模型选用的冲击能量较低,所以没有考虑损伤对冲击响应的影响.Shariyat 和Hosseini[23]提出了一种双叠加幂指数全局--局部理论,在改进赫兹接触理论的同时,分析了带黏弹性芯层的三明治层合板的低速冲击特性.该模型虽然有损伤产生,但是建模时也没有考虑其影响.
针对上述研究不足,本文结合经典层合板理论,冯·卡门假设和能量守恒定律,首次从解析角度提出了带黏弹性芯层的纤维金属混杂层合板在低速冲击激励下的动态响应预测模型.通过对金属层采用Von Mises 失效准则,对纤维层采用Tsai-Hill 失效准则和对黏弹性层采用指数Drucker-Prager 失效准则,考虑不同材料层对冲击动态响应的影响,推导获得了每次失效事件发生后的结构位移、能量和冲击接触力的表达式,还提出了结构动态响应分析的具体流程图.最后,基于自行设计的落锤试验系统开展了一系列测试,验证了所提出的理论预测模型的有效性.本文所采用的分析方法和模型可为带黏弹性芯层的纤维金属层合板的冲击问题研究,提供一种新思路和新模型.
1 理论模型
1.1 模型概述
所建立的VC-FMLPs 结构的冲击动力学模型如图1 所示,其长、宽、厚分别为a,b,h.其中,金属层厚度为hm,黏弹性层厚度为hv,每个纤维层厚度均相同且为hf.首先,以结构受到球头型圆柱杆冲击激励时的中心位置为原点,以该类型层合板的中面为参考平面,并沿着厚度方向,建立o-xyz坐标系.图中的1 代表纤维纵向,2 代表纤维横向,3 代表垂直于1-2 平面的方向.且纤维方向与整体坐标系x轴的夹角为θ.假设纤维增强复合薄板平行纤维方向的弹性模量为E1,垂直纤维方向的弹性模量为E2,1-2 平面内的剪切弹性模量为G12,1 方向作用应力引起1,2 方向应变的泊松比为ν12,2 方向作用应力引起1,2 方向应变的泊松比为ν21.金属层和黏弹性层的弹性模量分别EM和EV,剪切模量分别为GM和GV,泊松比分别为νM和νV.另外,V为球头型圆柱杆在接触VC-FMLPs 结构瞬间的速度,ξ 和ζ 为冲击位置参数,其取值范围分别为.

图1 嵌入黏弹性芯层的纤维金属混杂复合薄板理论模型Fig.1 The theoretical model of VC-FMLPs
1.2 本构关系
在冲击过程中,由于随着VC-FMLPs 结构的逐步破坏,其参考平面不断变化.因此,VC-FMLPs 结构的参考平面z0可表示为[24]
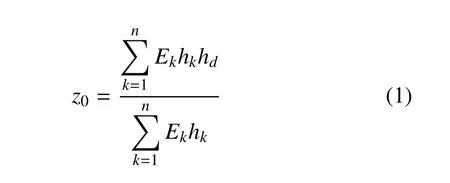
其中,Ek为第k层弹性模量,hk为第k层厚度,hd为第k层与球头型圆柱杆之间未被破坏层的总厚度.
由于冲击变形沿z轴方向的位移w远远大于沿x轴和y轴方向的位移u和v,因此忽略位移u和v.根据经典层合板理论,正应变εz和剪应变γyz,γxz都为0,即εz=γyz=γxz=0.结合冯·卡门假设,用中面位移w0表示VC-FMLPs 结构任意点的应变[25],可写为
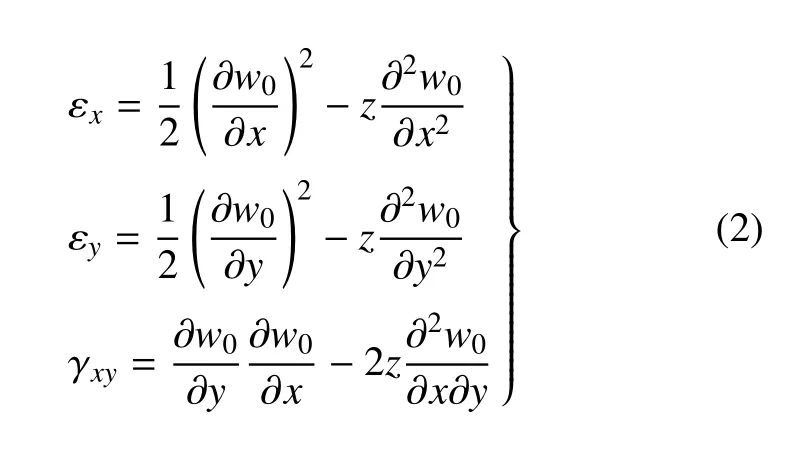
忽略应变率的影响[2,7-10],则材料在第k层主轴方向的应力--应变关系为

对于黏弹性层,式中的各个元素可表示为

对于金属层,式中的各个元素可表示为
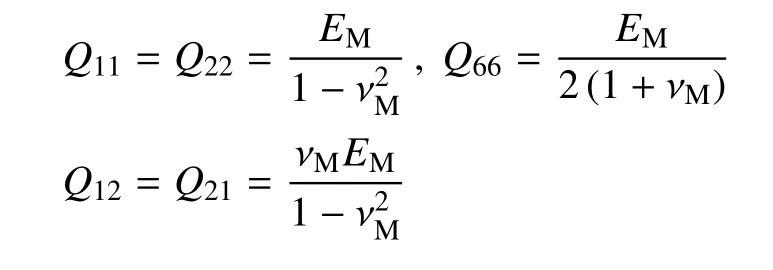
对于纤维层,式中的各个元素可表示为

当某一层失效后,失效层面内1 方向,2 方向以及3 方向上的应力,,会分配到剩余层.根据各层刚度的不同,第k层面内1 方向,2 方向以及3 方向分配得的应力,,为

其中,K1,K2和K12为VC-FMLPs 结构的等效刚度,其表达式为
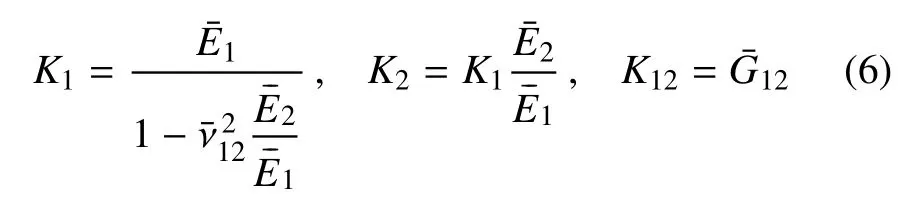
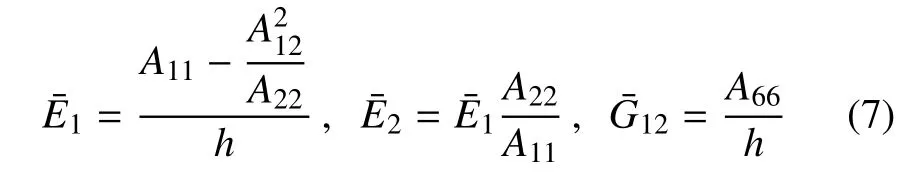
相应的等效泊松比是

式中,Aij,Bij,Dij分别为拉伸系数、拉伸弯曲耦合系数和弯曲系数,可写为
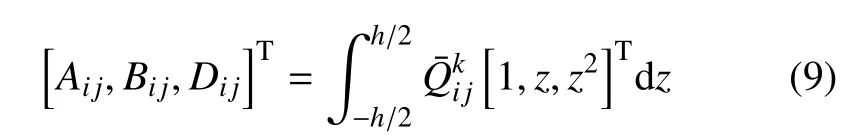
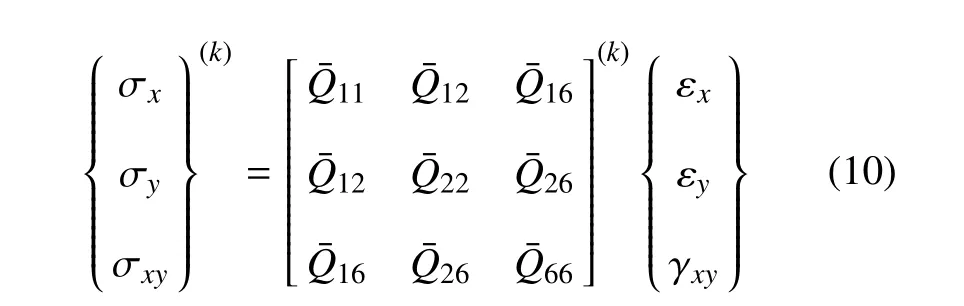
其中
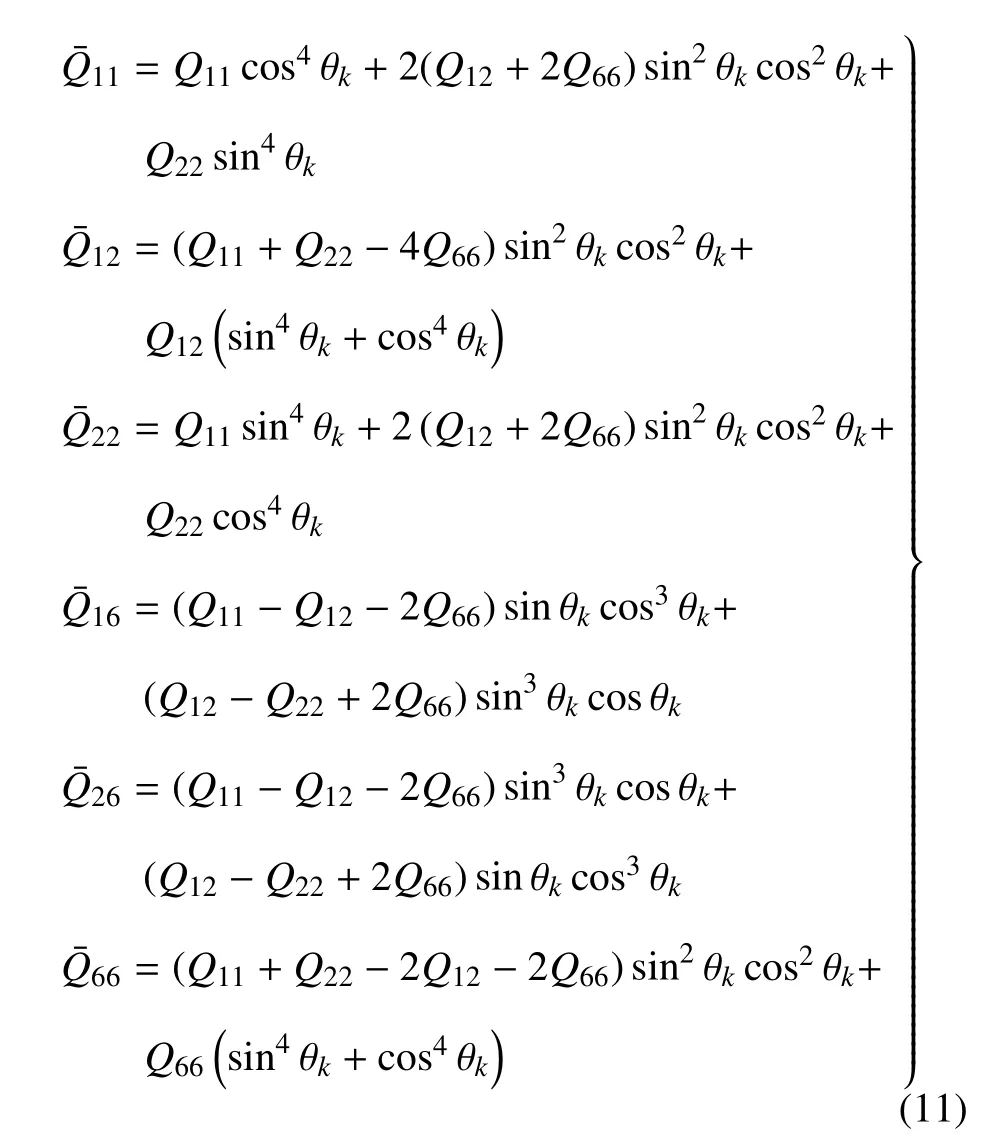
式中,θ 为第k层板的纤维方向与整体坐标系x轴的夹角.
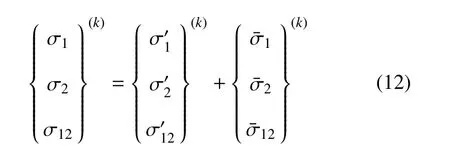
结合式(3)和式(5),就可以得到第k层面内1 方向,2 方向以及3 方向实际应力σ1,σ2,σ12为
1.3 失效准则
在文献[28-30]提出的低速冲击下层合板结构损伤失效准则的基础上,利用逐渐累积损伤分析方法,对于金属层,可应用Von Mises 等效应力失效准则[28]
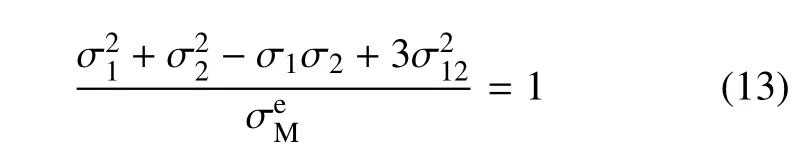
对于纤维层,应用Tsai-Hill 应力失效准则[29]
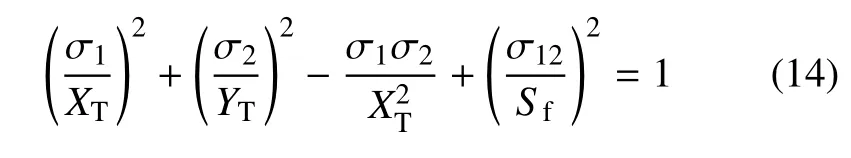
其中,XT为纤维纵向拉伸强度,YT为纤维横向拉伸强度,Sf为纤维的剪切强度.
对于黏弹性层,应用指数Drucker–Prager 应力失效准则[30]
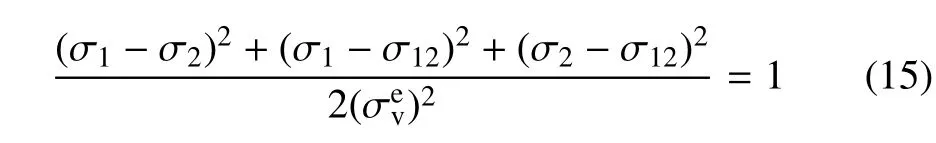

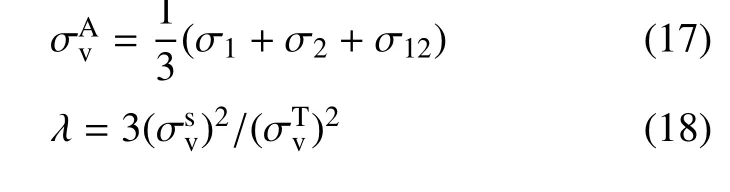
1.4 位移方程
在与球头型圆柱杆冲击接触过程中,VCFMLPs 结构将形成两个变形的区域,分别称其为接触区域与拉伸区域,如图2 所示.假设冲击过程中,损伤仅发生在接触区域内.在此区域内,需计算结构因塑性变形(及其损伤)消耗的能量以及因弹性变形产生的应变能;在拉伸区域内,只需计算因弹性变形产生的应变能.

图2 VC-FMLPs 结构变形区域Fig.2 The deformation region of FMLPs
对于接触区域,其主要由球头型圆柱杆形状决定,其范围可看作由冲击中心位置到接触半径,即.考虑到接触半径相对于该类型层合板的尺寸非常小,可将该接触区域近似看成一个平面.在这个范围内,中面位移w0(x,y)的表达式为

其中,wmax为冲击中心处的最大位移.
对于拉伸区域,其范围可看作由接触半径到结构约束边界组成,即Rxmax{ξ,a−ξ},Rymax{ζ,b−ζ}.对于图1 所示的四边固支边界下的VC-FMLPs 结构,w0(x,y)有如下关系式

为了解释不同材料层对VC-FMLPs 结构中面位移的贡献,改进文献[31]中的位移公式,引入金属体积分数vm,纤维层体积分数vf,黏弹性层体积分数vv,并使其满足式(20)中的边界条件
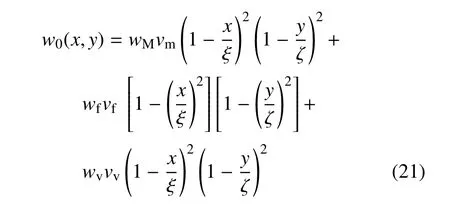
其中

在利用模型计算获得了中面位移后,将其代入式(2)、式(3)、式(5)和式(12)来获得变形最大位置处(在冲击中心位置处,近似取x=R,y=R处)应力,并进一步应用1.3 部分对应的失效准则来判别某层是否发生失效.如果式(13)或式(14)或式(15)对应的左侧表达式大于1,则认为该层发生了损伤(此时,可认为满足了失效准则要求,并可将对应的接触区域内刚度设置为零);如果没有发生失效,则将中面位移对应的wmax进行更新,并在获得新的中面位移基础上,重复利用式(13)或式(14)或式(15)进行判别,直到满足失效准则的要求为止.
2 冲击响应求解
2.1 冲击接触力的计算
由球头型圆柱杆冲击产生的总动能T为

VC-FMLPs 结构的应变能为
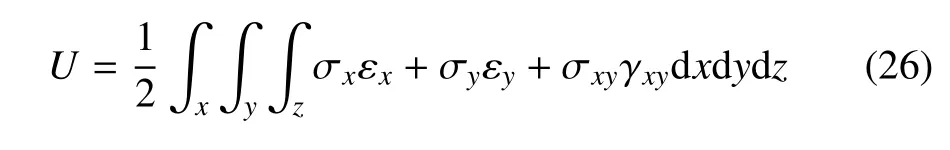
将式(2)、式(9)和式(10)代入式(26)中,可得到VC-FMLPs 结构由拉伸变形产生的应变能Um

VC-FMLPs 结构拉伸弯曲耦合应变能Uc为

VC-FMLPs 结构弯曲产生的应变能Ub为
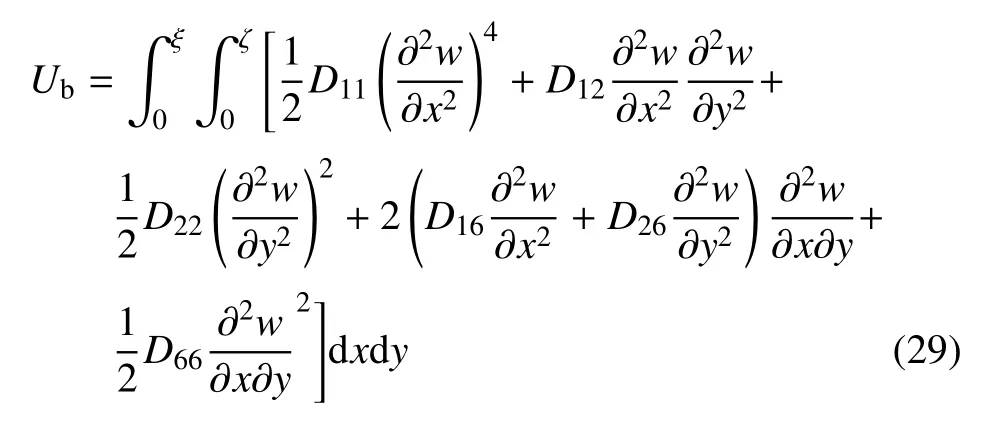
这里,需要说明的是,式(27),式(28)和式(29)只是对VC-FMLPs 结构在xoy面内的第一象限积分后的应变能结果,结构的总应变能需要对4 个象限要分别积分,并进行叠加才可获得.
冲击接触力F所做的功为

VC-FMLPs 结构总势能Us表达式为
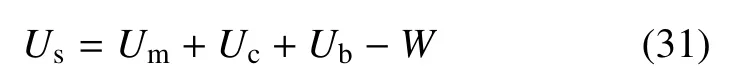
当∂Us/∂wmax=0 时,Us会获得最大值,此时,可计算获得冲击接触力F
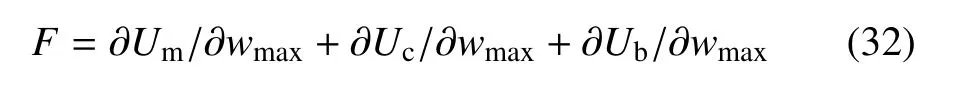
2.2 失效模式
首先,为了求解方便,引入冲击“失效事件”的概念[32],假设该事件是由冲击造成的VC-FMLPs 结构在接触区域的分层损伤和断裂效应引发的,则每个失效事件j吸收的总应变能Uj可表示为

参考文献[32],可获得x=Rj,y=0 处变形协调条件,并得到下列等式条件

其中,Rj为第j个失效事件时的接触半径,Rmax为球头型圆柱杆球头半径.这样,Rj就通过式(34)求解获得.
第j次失效事件中,因分层损伤消耗的能量为

其中,et为某层能量密度.对于纤维层、金属层以及黏弹性层,其能量密度,和分别为

进一步,由能量守恒定律可获得每次失效事件j发生后的冲击速度的表达式
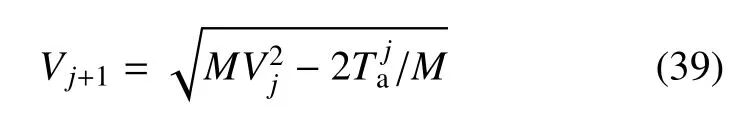
另外,根据参考文献[31],采用一个单自由度弹簧--质量--阻尼模型来描述VC-FMLPs 结构在球头型圆柱杆冲击下的整个过程.则第j次失效事件中的接触力Fj可由动力学方程表示
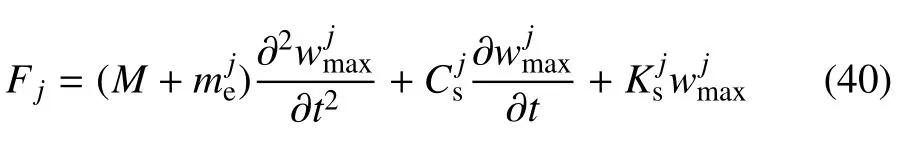
其中,M为球头型圆柱杆质量,和为第j次失效事件时VC-FMLPs 结构受冲击作用影响的的等效质量和冲击中心处最大位移,,为分别为结构整体剪切刚度和黏滞阻尼系数.
进一步可得第j次失效事件对应的动力学方程
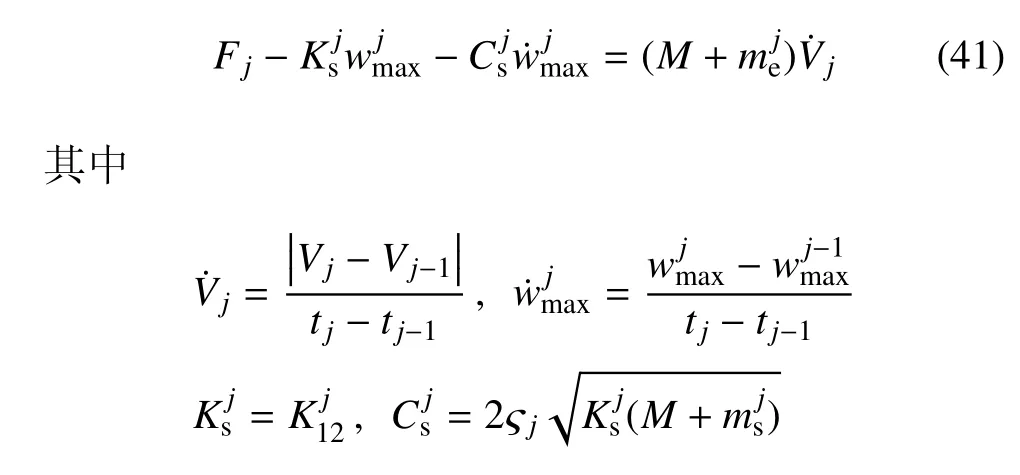
为失效事件j发生时结构整体剪切刚度,ςj第失效事件j发生时的等效阻尼比.Vj,Vj−1,,以及tj和tj−1分别代表了第j次失效事件和第j−1 次失效事件中的速度,冲击中心处最大位移和时间.
第j次失效事件对应的动能可表示为
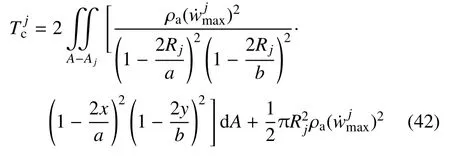
其中,ρa为VC-FMLPs 结构的面密度,A为其整体积分区域,Aj为接触区域.
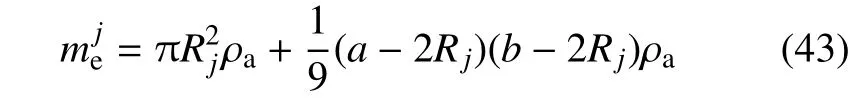
如此,可根据式(41),确定失效事件j发生的时间tj
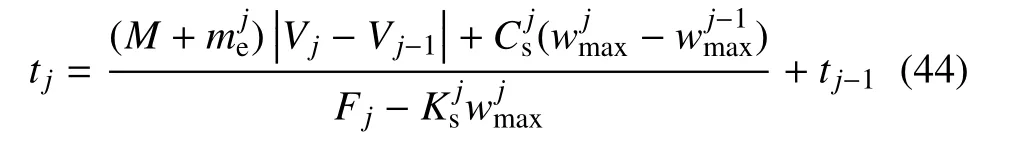
至此,就实现了VC-FMLPs 结构冲击动态响应的理论求解,其详细的分析流程如图3 所示.当失效事件j发生时,通过式(33)求解结构系统吸收的总应变能Uj,通过式(35)和式(36)求解接触区域,因分层损伤消耗的能量和塑性变形消耗的能量,进而求解冲击接触力Fj、位移和失效事件j发生的时间tj,直至球头型圆柱杆冲击能量消耗为零,输出计算结果.
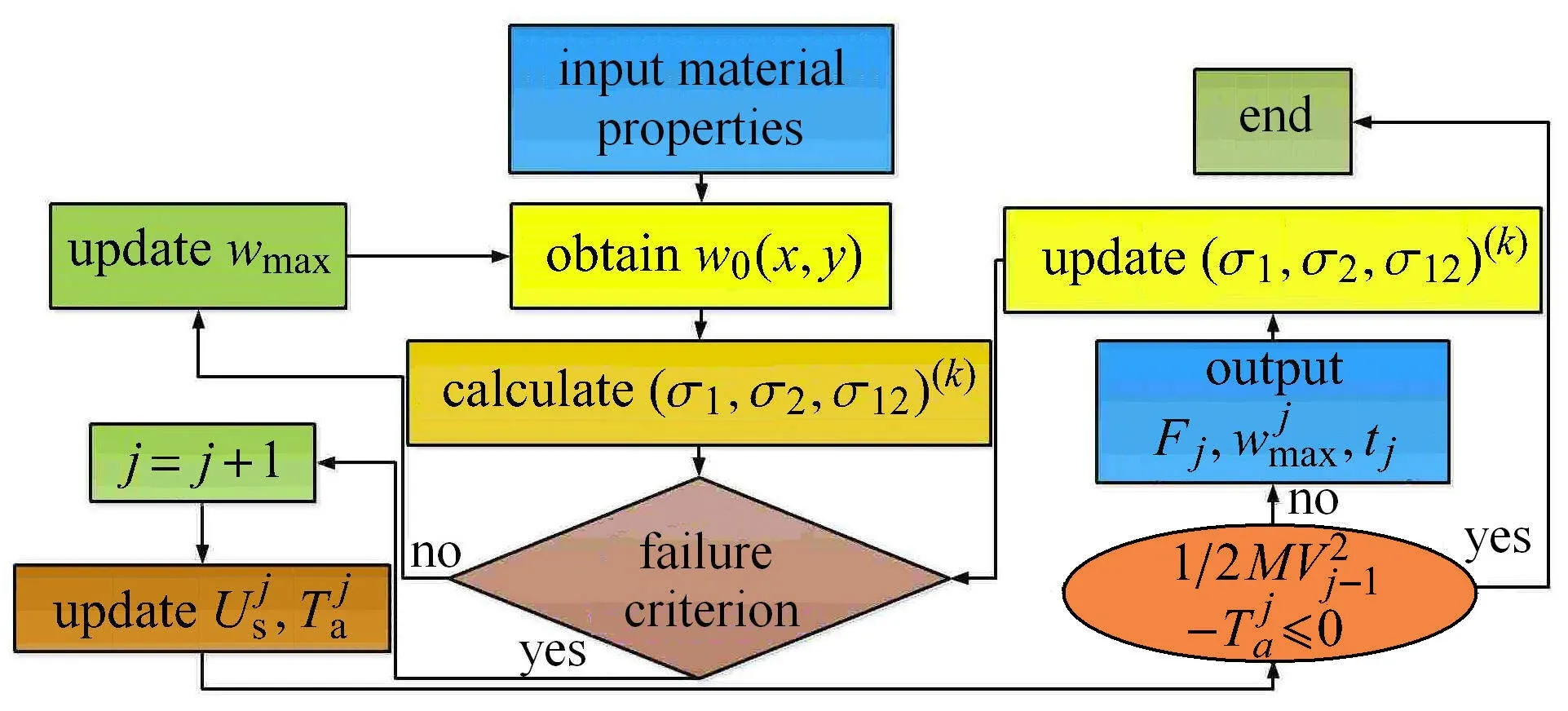
图3 低速冲击激励下VC-FMLPs 结构动态响应分析流程图Fig.3 Flow chart of dynamic response analysis of VC-FMLPs under low-velocity impact excitation
3 实验验证
图4 给出了自行设计的VC-FMLPs 结构落锤冲击试验系统,落锤质量为1 kg,刚性冲头的顶端被设计成半球形状(直径8.0 mm).在冲击测试过程中,通过磁力表座固定在冲头上的LSM 位移传感器和嵌入式动态力传感器(型号为联能CL-YD-305),并利用LMS 数据采集仪和笔记本工作站,可实时采集并记录结构在低速冲击下的冲击接触力和响应数据.试验系统经过“江苏联能电子技术有限公司”和“KISTLER”专业技术员的调试和校准,并在正式实验前进行多次预实验,保证了实验结果的可重复性.

图4 落锤低速冲击试验设备Fig.4 Drop weight impact tester
以嵌入Zn33 黏弹性芯层的TA2 钛合金混杂T300 碳纤维/树脂基层合板为对象,通过夹具夹紧其四边,夹持后长、宽、厚为170 mm×160 mm×2.6 mm,如图5 所示.其中金属外层厚度为0.3 mm,EM=108 GPa,νM=0.3,ρM=4150 kg/m3,=600 MPa;纤维层为对称正交铺设[0◦/90◦/0◦/90◦] 的TC300 碳纤维/E21 环氧树脂,共有9 层,E1=136 GPa,E2=7.92 GPa,G12=3.39 GPa,ν12=0.32,ρf=1780 kg/m3,XT=2210 MPa,YT=49 MPa,Sf=135 MPa;黏弹性层厚度为1 mm,EV=5 MPa,νV=0.3,ρV=4510 kg/m3,=7 MPa.

图5 VC-FMLPs 结构试验件及夹具Fig.5 Test piece and fixtures of VC-FMLPs
在落锤高度为0.6 m 和1 m 处(即冲击能量为5.9 J 和9.8 J 时),分别开展冲击实验,图6 给出了测试获得的VC-FMLPs 结构的冲击接触力、位移响应和冲击载荷--位移曲线.为了方便与实验数据进行对比,将利用第1 部分建立的理论模型计算获得的分析结果也一并绘制在图7 上,还以图中的峰值结果作为统计,给出了相应的计算相对误差.另外,以冲击能量达到9.8 J 为例,图7 给出了结构在冲击面和非冲击面产生的损伤照片.
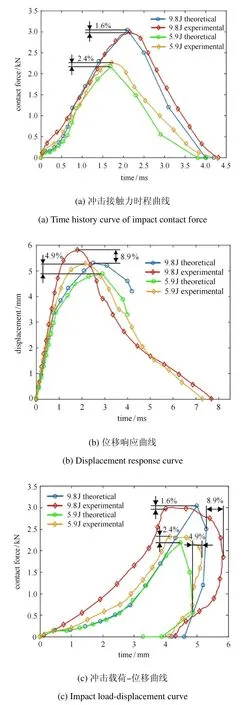
图6 理论和测试获得的低速冲击下VC-FMLPs 结构的冲击接触力时程曲线、位移响应曲线和冲击载荷--位移曲线Fig.6 Impact contact force time-history curve,displacement response curve and load-displacement curve of VC-FMLPs under low-velocity impact obtained by theory and test

图7 冲击能量为9.8 J 时VC-FMLPs 结构的冲击损伤Fig.7 Impact damage of VC-FMLPs under the impact energy of 9.8 J
通过对上述结果进行分析可知:利用该理论模型,计算获得的VC-FMLPs 结构冲击下的冲击接触力时程曲线、位移响应以及冲击载荷--位移曲线与实验结果的变化趋势吻合较好,且关注的曲线上峰值点的计算误差最大不超过9%(详见图6),进而验证了所建立的动态响应预测模型及其分析方法的正确性,可以利用该模型对VC-FMLPs 结构的冲击响应进行较为可靠的预测和分析.另外,需要说明的是,利用该模型完成上述计算的时间在3 min以内,相对于商用软件ANSYS 的LS-DYNA 模块,大大提高了计算效率(其通常花费3∼5 h).
但仍有必要对模型的局限性问题进行分析:(1)建模时忽略了已失效层在冲击过程中的持续损伤累积,这也是计算误差的来源之一;(2)认为每个失效事件发生时,将接触区域内刚度整体清零,在后续的研究中,应在考虑损伤区域的剩余刚度;(3)由于该模型没有考虑应变率等因素的影响,因而不适合预测高速冲击问题;(4)由于模型需要进行足够次数的迭代,才能进行高精度预测,如果是太低速的冲击,则会因迭代次数过少而影响计算精度.因此,参考相关文献的假设条件[2],推荐该模型适用的冲击速度范围为2∼10 m/s.
4 结论
本文建立了低速冲击激励下嵌入黏弹性阻尼芯层的纤维金属混杂层合板动态响应预测模型,并对其分析获得的冲击接触力、位移响应以及冲击载荷--位移曲线进行了测试验证.结果表明,理论计算与获得的上述冲击参数的变化趋势与实验吻合较好,且关注的曲线上峰值点的计算误差最大不超过9%,进而验证了理论模型和分析方法的正确性.另外,相对于ANSYS 的LS-DYNA 模块,该模型大大提高了计算效率,可为复杂层合板结构动态冲击问题的高效求解提供一种新思路和新手段.

