折叠翼飞行器的动力学建模与稳定控制1)
宋慧心 金磊
(北京航空航天大学宇航学院,北京 100191)
引言
变体飞行器是一种能够根据不同的飞行环境改变构型,实现最佳的气动性能,完成多种飞行任务的飞行器[1].作为变体飞行器的一种,折叠翼飞行器能够通过机翼的折叠改变自身构型[2],以不同的构型完成不同的飞行任务.机翼折叠时,翼面积、展长减小,后掠角增大,适合低空高速飞行,机翼展开时,翼面积和展长增大,升阻比增大,适合于高空长航时飞行,节省能耗[3].
作为一类新型飞行器,折叠翼在带来优势的同时也带来了一些问题.机翼的折叠所带来的额外自由度使得飞行器的动力学模型变得更加复杂,而由变形引起的气动力与气动力矩、压心、质心和转动惯量等参数的变化以及附加力和附加力矩的产生都会给飞行器的稳定性和操纵性带来很大的影响[4],严重的甚至会失稳,由此对飞行器的控制性能提出了更高的要求.
常用于建立折叠翼飞行器多刚体动力学模型的方法主要有3 种:Newton-Euler 方法、Lagrange 方程、Kane 方法.Yue 等[5]使用Newton-Euler 方法建立了折叠翼变形飞行器的六自由度非线性动力学模型,并对其进行解耦,研究了飞行器的纵向动力学响应.Grant 等[6]利用Newton-Euler 建立了变后掠飞行器的动力学模型,并研究了飞行器的时变惯性效应.郭建国等[7]利用Newton-Euler 方法建立了非对称伸缩翼变形飞行器的动力学模型,并进行了动态特性分析.Seigler 等[8]使用Kane 方法对建立了大型变形飞行器的六自由度非线性动力学模型.Obradovic 等[9]在考虑气动性能和惯性性能变化的情况系使用Kane方法建立了变形飞行器的六自由度非线性模型.Zhu等[10]使用Kane 方法建立了变跨度变掠飞行器的六自由度非线性动力学模型.张杰等[11]利用Kane 方法建立了变展长变后掠飞行器的六自由度动力学模型,并进行了动态特性分析.
针对变体飞行器的控制,国内外已有很多学者展开了研究.针对变体飞行器的控制方法,常用的方法是将变体非线性控制器的动力学模型利用小扰动原理进行线性化,得到变体飞行器的线性变参数(linear parameter varying,LPV)模型,然后设计控制器实现相应的控制目标[12].Wen 等[13]提出了一种基于LPV方法有限时间收敛滑模控制策略,用于变形飞机在参数不确定和外界干扰下的稳定性控制.Guo 等[14]通过对动力学模型的线性化,设计H∞跟踪控制器实现了鸥翼变形飞行器的跟踪控制.Lee 等[15]针对变跨度变掠飞行器设计了一种基于LPV 模型的增益调度反馈控制器.程昊宇等[16]在考虑存在有界干扰和控制器参数不确定性情况下,设计了基于LPV 模型的非脆弱有限时间鲁棒控制器实现了变体飞行器的稳定控制.陶晓荣等[17]基于LPV 模型设计了鲁棒最优控制方法,实现了机翼机翼扭转变形跟踪控制.夏川等[18]基于LPV 模型设计了有限时间H∞跟踪控制.刘玮等[19]设计了基于LPV 模型的鲁棒变增益控制器实现折叠翼飞行器的稳定控制.
LPV 模型只适用于小扰动情况,当飞行器做大角度机动时,若仍采用此方法将严重影响控制精度甚至无法实现稳定控制.自抗扰控制(active disturbance rejection control,ADRC)是由韩京清[20]提出的一类非线性控制方法.ADRC[21]主要由跟踪微分器(tracking differentiator,TD)、扩张状态观测器(extended state observer,ESO)、非线性反馈控制律(nonlinear states error feedback,NLSEF) 三部分组成[21].ADRC 的核心是ESO,ESO 能够实时地对系统的内外干扰进行估计,不依赖于系统的精确数学模型,通过设计控制器能够将对内外干扰进行补偿,从而得到等效的线性系统,使用线性系统的控制方法就能够实现对整个系统的控制[22].自抗扰控制技术的稳定性证明是一个难点,2000 年黄一和韩京清[23]以二阶系统为例,完成了扩张观测器的稳定性证明.韩京清、张荣[24]以二阶系统为例,分析了扩张观测器的误差,并且给出了提高扩张观测器精度的参数所应该满足的条件.赵志良[25]发现了韩京清和王伟[26]对自抗扰控制器中的跟踪微分器证明的不合理之处,以二阶系统为例,证明了跟踪微分器、扩张状态观测器、基于扩张状态观测器的反馈控制稳定性.
本文针对折叠翼飞行器,利用凯恩方法建立了六自由度多体非线性动力学模型,通过气动计算拟合了气动参数与折叠角的函数关系并分析了机翼折叠过程中的动态特性.针对飞行器纵向非线性模型,提出了一种基于自抗扰理论的稳定控制方法.此方法不需要对动力学模型进行小扰动线性化,而是通过设计扩张状态观测器(ESO)将系统中存在的非线性项、耦合项以及参数时变项等内外总扰动进行实时估计和补偿,从而得到等效的线性模型,通过设计线性控制器即可实现飞行器变形过程中的高精度稳定控制.
1 折叠翼飞行器的动力学建模
本文以轻型飞机Navion L-17[27]作为研究对象,基于kane 方法建立折叠翼飞行器的动力学模型.如图1 所示,假设左右机翼质量相同,几何形状完全对称,将机翼分为内翼和外翼,折叠时,内翼相对机体折叠,外翼相对机体始终保持水平.机翼对称折叠,左右内翼折叠角大小为δ,如图2 所示.

图1 机翼折叠过程示意图Fig.1 Schematic of morphing process
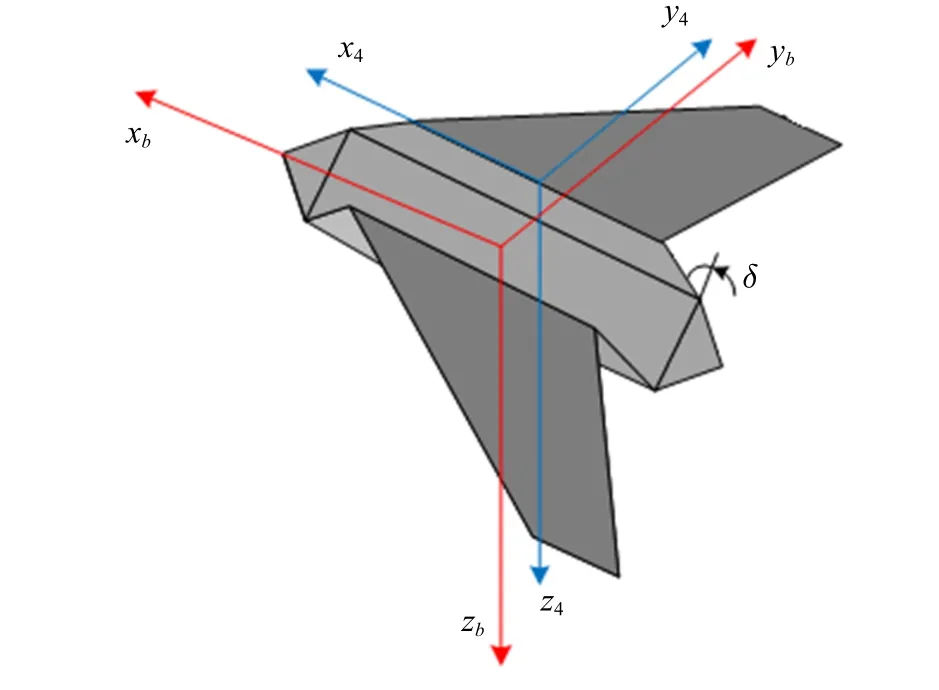
图2 飞行器坐标示意图Fig.2 Schematic of morphing aircraft coordinate
将机体看作主刚体,折叠翼看作从刚体,整个系统可看由5 个独立刚体组成的多刚体系统[28],质量为mi(i=b,1,2,3,4),其中,b 表示机体,1 表示左折叠翼内翼,2 表示左折叠翼外翼,3 表示右折叠翼内翼,4表示右折叠翼外翼,总质量为m.
为描述各刚体的运动,定义以下坐标系:
(1)地面坐标系fg−Ogxgygzg:原点Og为起飞点,xg轴是航迹面与水平面的交线,指向飞行目的地为正,zg轴垂直于地平面,向下指向地心,yg轴与xg轴和zg轴构成右手坐标系.
(2) 机体坐标系fb−Obxbybzb:坐标原点取在机体质心,xb轴位于飞机对称面内与飞机的轴线平行并指向机头方向,yb轴垂直于机体对称面并指向右侧机翼,zb轴在飞机对称面内,与xb轴垂直指向机身下方.
(3)折叠翼固连坐标系fi−Oixiyizi:原点位于折叠翼旋转轴几何中心处,xi轴与折叠翼的旋转轴重合,且与机体轴的xb轴同向,yi轴垂直于xi轴并且位于折叠翼面内,随翼面转动,zi轴与xi轴和yi轴构成右手坐标系.
(4) 气流坐标系fa−Oxayaza:坐标原点取在飞机质心,xa轴与飞机速度矢量的方向重合,za轴位于飞机对称面内并与xa轴垂直指向机体下方,ya轴与xa轴和za轴构成右手坐标系.
刚体上取质量参考点dmi,根据各刚体的约束关系,求取各刚体速度矢量vi和加速度矢量ai.选取广义速率分别为机体的速度vb和角速度ωb,求取各刚体速度矢量相对于广义速率的偏速度分别为和.
根据Kane 方法分别求取广义惯性力和广义主动力,由此得到机体系下的系统平动方程和转动方程分别为

式中,vb表示机体的速度在机体系下的分量列阵,在气流系下表示为=[V0 0]T,上标a表示气流系,V表示飞行速率;ωb表示机体系相对于地面系的角速度在机体系下的分量列阵,记为ωb=[p q r]T;F表示系统所受到的合外力在机体系下的分量列阵,包括气动力、推力和重力;FS表示机翼折叠带来的附加力在机体系下的分量列阵;I表示飞行器相对于Ob的转动惯量在fb下的投影;MA表示飞行器所受到的气动力矩在机体系下的分量列阵;MS表示机体折叠带来的附加力矩在机体系下的分量列阵.
附加力与附加力矩在机体系下的表示为

式中,R,rb1,rb3,r12和r34分别表示Og到Ob的位置矢量在fg下的分量列阵、Ob到O1和O3的位置矢量在fb下的分量列阵、O1到O2的位置矢量在f1下的分量列阵、O3到O4的位置矢量在f3下的分量列阵;变量上“.” 表示在投影坐标系下求对时间求一阶导,变量上“..”表示在投影连坐标系下求对时间求二阶导,上标“×”表示变量的叉乘;Aij表示fj到fi的转换矩阵;Ωi和ωi分别表示fi相对于fg的角速度在fi下的分量列阵、fi相对于fb的角速度在fi下的分量列阵;Si,Ii和IΩi表示第i个机翼对Oi的静矩、转动惯量矩阵和拟惯量矩阵在fi下的投影,表示为

式中,ri表示fi原点到dmi的位置矢量在fi下的分量列阵.
Sbi,Ibi和分别表示第i个机翼相对于Ob原点的静矩分量列阵、转动惯量矩阵和耦合转动惯量矩阵在fb下的投影,表示为

式中,rbi表示Ob到Oi的位置矢量在在fb下的分量列阵;Abi表示fi到fb的转换矩阵,且有Aib=.
由于机翼折叠只改变飞行器的动力学方程,并不改变飞行器的运动学方程和导航方程,根据文献[29]可得到飞行器的运动方程和导航方程,此处不再赘述.
2 折叠翼飞行器的纵向运动方程
为了简化计算方程,根据水平无侧滑条件即滚转角ϕ、侧滑角β 满足ϕ=β=0 与p=r=0 将动力学方程进行解耦得到飞行器的纵向动力学方程,以研究机翼折叠过程中纵向飞行参数的变化.解耦得到的飞行器纵向运动方程如下式所示

式中,α 和θ 分别表示攻角和俯仰角;h表示飞行高度;T表示发动机推力,T=kTδT,kT表示推力系数,δT表示油门开度;g表示重力加速度;Iyy表示I中绕yb轴的主轴转动惯量;Fs1表示附加力在速度方向的分量、Fs2表示附加力在速度的垂直方向的分量;MSy表示附加力矩MS在机体系yb轴下的分量;L,D和MAy分别表示升力、阻力和俯仰力矩,其表达式为

式中,ρ 表示空气密度;Sw表示机翼的参考面积;cA表示平均气动弦长;CL,CD和Cm分别表示升力系数、阻力系数和俯仰力矩系数,与攻角α、舵偏角δe之间的线性函数关系可近似表示为[30]
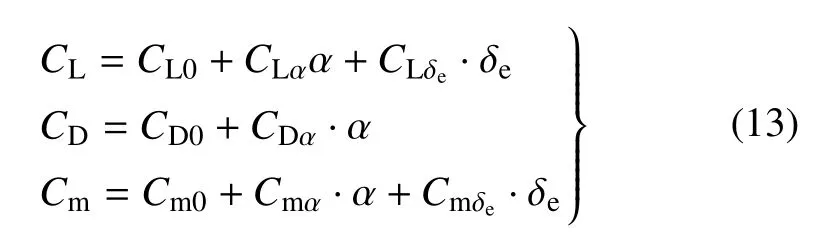
式中,CL0,CD0和Cm0分别表示基本升力系数、零升阻力系数、零升俯仰力矩系数;CLα和Cmα分别表示升力系数和俯仰力矩系数对迎角的导数;CLδe和Cmδe分别表示升力系数和俯仰力矩系数对舵偏角的导数.
3 折叠翼飞行器的气动建模与纵向动态特性分析
折叠翼飞行器在变形过程中,其受到的气动力和力矩会随着折叠角变化而发生大幅变化[31],为了在后续控制器设计与数值仿真中准确模拟气动,需要首先计算得到不同折叠角对应的气动数据并拟合出关于折叠角的函数.DATCOM 软件能够利用飞行器的外形快速得到大量气动参数,计算便捷,适用于飞行器的理论验证阶段.使用DATCOM 软件,通过改变机身外的半翼展SSPNE、理论半翼展SSPN、内翼后掠角SAVSI 和内翼上反角DHDADI 来实现机翼的折叠[3],计算参数计算见表1(表中1 ft=30.48 cm).
将表1 中的数据输入到DATCOM 软件中,可以得到相关的气动参数.利用MATLAB 插值拟合可得到各气动参数与折叠角之间的函数关系
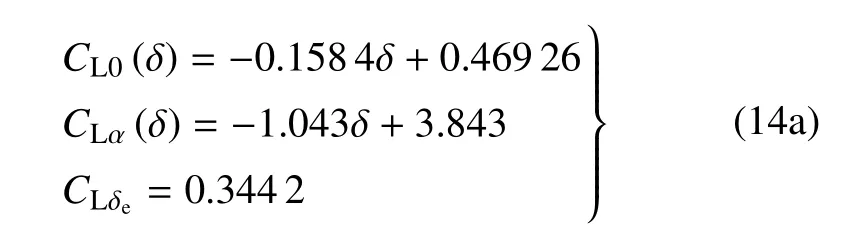

式中,δ 表示折叠角.将式(14) 代入式(13),再将式(13)代入式(12)即可得到不同折叠角下升力、阻力和俯仰力矩.

表1 机翼折叠过程示意图Table 1 Morphing wing shape parameter
为了研究机翼折叠过程中飞行参数的变化,对飞行器的纵向运动响应进行仿真[32].仿真初始条件为:高度4000 m,速度0.4 Ma,分别使机翼以2(◦)/s,5(◦)/s,10(◦)/s 的折叠角速度折叠60◦,研究纵向动力学状态变量在变形过程中的变化.根据数值仿真,可以得到飞行参数变化图如图3 ∼图8 所示.

图3 折叠角随时间的变化图Fig.3 Schematic of folding angle

图4 速度增量变化图Fig.4 Schematic of speed increment

图5 攻角增量变化图Fig.5 Schematic of angle of attack increment
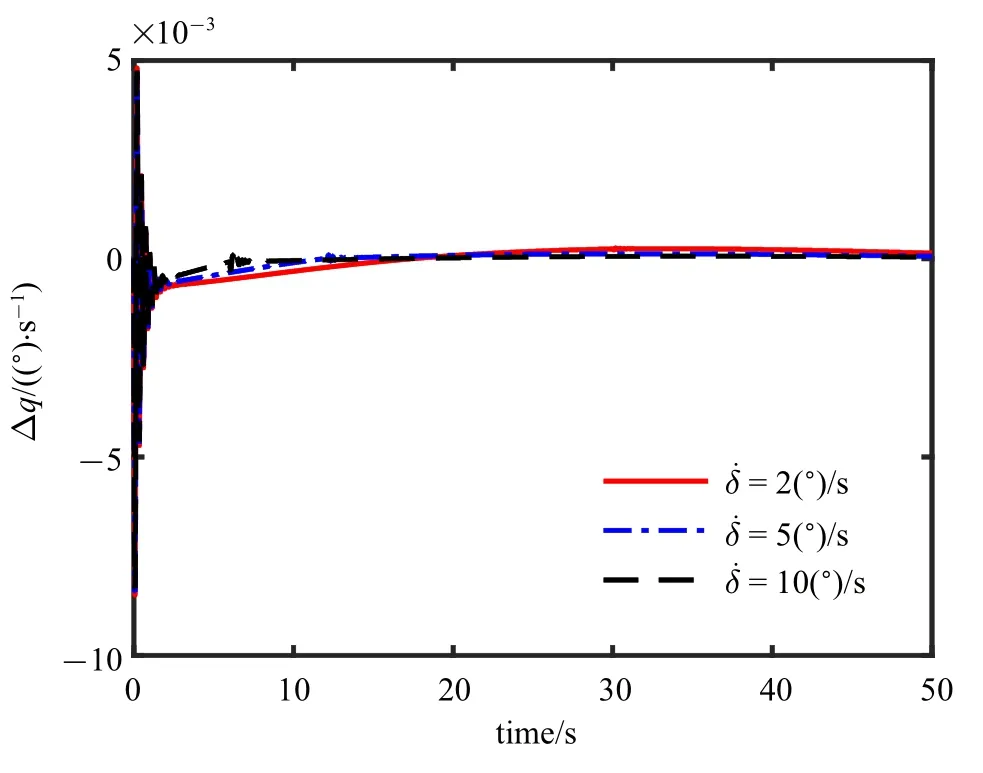
图6 俯仰角速度增量变化图Fig.6 Schematic of pitch angular velocity increment
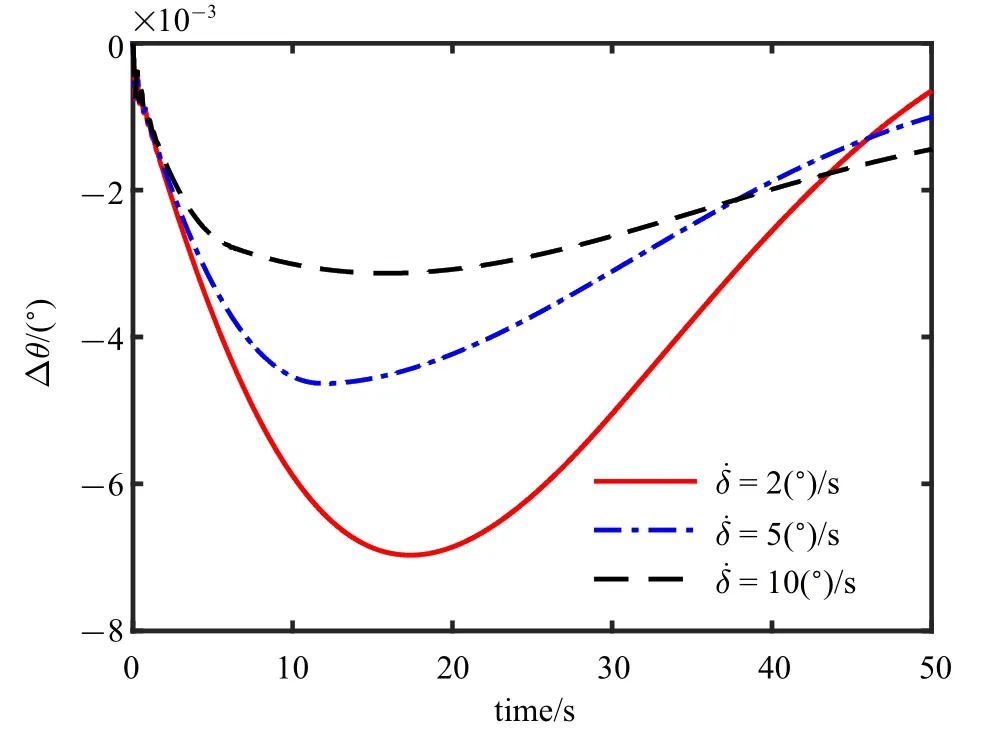
图7 俯仰角增量变化图Fig.7 Schematic of pitch angular increment
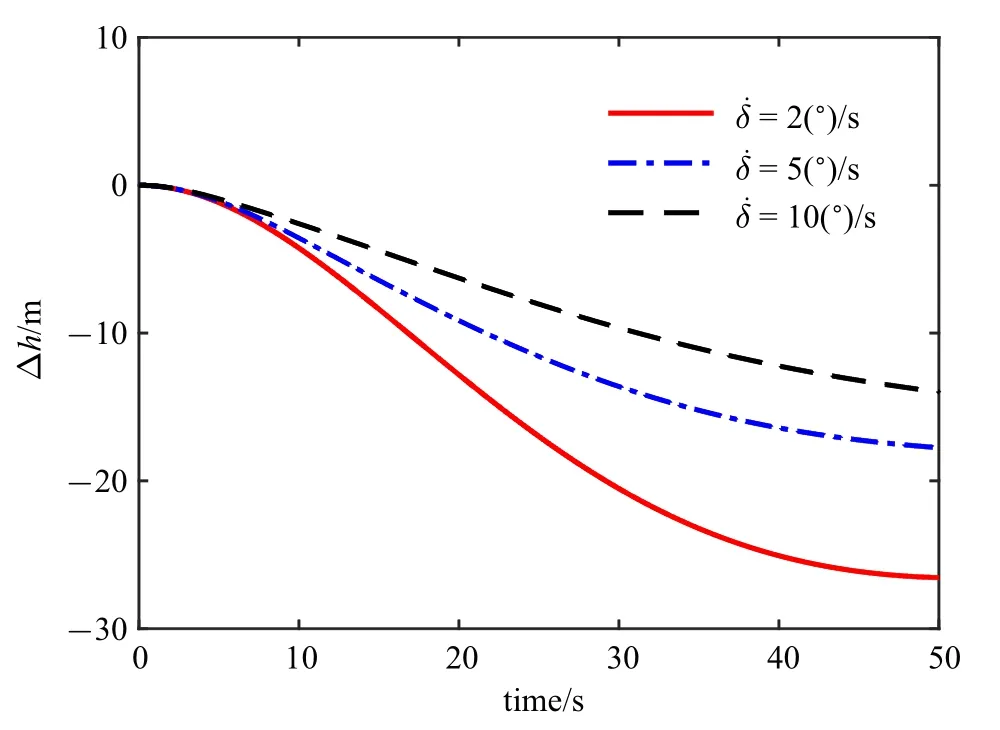
图8 高度增量变化图Fig.8 Schematic of height increment
从图3 ∼图8 中可以看出,机翼刚开始折叠时,俯仰角速度增量变为负值,俯仰角减小,这是因为在刚开始折叠时,飞机的升力面后移,导致气动中心后移,从而产生了低头力矩.随着折叠角的增大,飞机的速度增大,高度减小,这是因为折叠角增大时,机翼的面积和展长变小,从而导致升力减小,其在竖直方向的分量不足以平衡重力,从而导致了高度的减小,同时推力大于阻力,从而导致速度的增大.变形结束后,气动中心停止后移,此时的升力在竖直面内的分量仍然小于重力,高度继续下降,阻力仍然小于推力,速度继续增大.而俯仰角和攻角开始回升,使得升力逐渐增大,直到与重力平衡,到达新的平衡状态.由于机翼折叠后,机翼的面积和展长减小,会使得升力减小,故新的平衡状态下的推力会减小.
当折叠速度不同而折叠角度相同时,折叠角速度越大,飞行参数的变化越小,这是因为折叠角速度越大,力和力矩的变化越快,参数恢复得也越快,而不同的折叠角速度导致的最终平衡态差别并不大,所以在变形过程中,为了使飞机更快地回到平衡态,可以选择稍大的折叠角速度.
4 基于自抗扰理论的稳定控制器设计
根据纵向动态特性可知,机翼折叠过程中,飞机的速度、攻角、俯仰角和高度均无法保持稳定,故需要设计稳定控制器进行变形过程中的稳定控制.自抗扰控制是韩京清提出的一种非线性控制方法[20],其原理是将系统外部扰动、参数摄动、未建模动态、系统内部各状态耦合影响等所有不确定因素都归结为系统总扰动并通过ESO 进行实时估计,进而实现对扰动的补偿[33].
本文基于自抗扰控制理论,将折叠翼飞行器纵向动力学中的非线性项、时变项和耦合项作为系统总扰动,分别针对速度通道和高度通道,设计基于ESO的反馈控制律对飞行器进行稳定控制,控制结构图如图9 所示.
4.1 速度通道
根据式(11)∼式(14)将速度通道写成以下形式

式中,fV为非线性项,bV为控制系数,其表达式为

bV为时变量,而要实现自抗扰控制,只需要知道bV的估计值即可,取变形前的初始值作为其估计值,即

式中,α0为初始平衡时的攻角.则式(15)等效为

式中,fV1=fV+(bV−bV0)δT为新的总扰动形式,UV=bV0δT为等效控制量.
设计二阶ESO 为

式中,zv1是ESO 对实际速度的估计,zv2是对速度通道总扰动fv1的估计.非线性函数fal(ev1,av1,δv1) 的表达式为

式中,αv1和δv1为可调参数,0 < αv1< 1,δv1> 0.只要参数βv1和βv2选择合适,满足收敛和稳定条件,当其稳定时,ESO 状态将满足以下收敛关系

图9 自抗扰控制流程图Fig.9 Schematic of active disturbance control

由此可知,若利用估计量zv2对速度通道(18)实施动态反馈控制补偿

则式(18)可化为一阶线性系统

针对补偿后的一阶线性系统设计PD 控制器为

式中,Vc为指令速度.最终得到油门开度指令控制量为

为了从理论上验证算法的合理性,基于自稳定域理论来证明ESO 与控制器的稳定性.令x1=V,x2=fV1,w=,其中,w有界,|w| 令e1=zv1−x1,e2=zv2−x2,ev1=e1,fc=fal(e1,av1,δv1),可知则状态误差方程为 定义函数 对于上述定义的函数V1,根据文献[34]可得到如下定理 引理1区域为系统(26)的自稳定域. 定理1对于闭环系统(26),假定w有界,即|w| 证明:当|h2(e1,e2)| >g1(e1,e2) 时,对式(28) 求导,可以得到 当|h2(e1,e2)|g1(e1,e2),即 定理1 得证,ESO 收敛. 由式(24)可知,对ev求导,可以得到 由此可以得到 定义Lyapunov 函数 则有 定义函数V=V1+V2,当满足条件(32)和(33)时,<0,控制器稳定. 将高度通道分为内外环,其中,俯仰角回路为内环,控制量为舵偏角δe,高度回路为外环.首先,设计PID 控制器进行指令高度的稳定控制,并得到指令俯仰角.然后基于自抗扰理论设计俯仰回路控制器,通过控制舵偏角,保证实际舵偏角跟踪指令俯仰角. 外环高度回路中,根据式(11) 中的高度方程直接设计PID 跟踪控制器为 式中,hc为指令速度,控制量θc将作为内回路的指令值. 内环俯仰回路中,根据式(11)∼式(14)将俯仰回路写为如下形式 式中,fθ为非线性项,bθ为控制系数,表达式为 为实现自抗扰控制,取bθ初始值作为其估计值,故有 式中,V0表示初始速度.式(41)可等效为 式中,fθ1=fθ+(bθ−bθ0)uθ为新总扰动形式,Uθ=bθ0δe为等效控制量. 设计俯仰回路的三阶ESO 为 式中,zθ1是ESO 对俯仰角θ 的估计,zθ2是ESO 对俯仰角速度q的估计,zθ3是对俯仰回路总扰动fθ1的估计.只要参数βθ1,βθ2,βθ3选择合适,满足收敛和稳定条件,当其稳定时,ESO 状态将满足以下收敛关系 利用估计量zθ3对俯仰回路(44) 实施动态反馈控制补偿 则式(44)可化为二阶线性系统 针对补偿后的二阶系统(48)设计PD 反馈控制器 最终得到舵偏角的控制指令为 稳定性证明与速度通道的证明类似,此处不再赘述. 基于非线性动力学模型和控制器模型,在MATLAB 中进行仿真分析.飞行器的基本参数:质量m=1247 kg,俯仰转动惯量Iyy=4067.3 kg·m2,机翼参考面积Sw=17.09 m2,平均几何弦长cA=1.74 m.初始状态为:速度V0=0.4 Ma,高度h0=4000 m,俯仰角θ0=4◦,攻角α0=4◦,俯仰角速度q0=0(◦)/s.ESO 的初始值为:zv10=0.4 Ma,zv20=0,zθ10=4◦,zθ20=0,zθ30=0.通过调试得到控制器参数,速度通道:βv1=250,βv2=2500,αv1=0.5,δv1=0.009,kPv=100,kdv=1000; 俯仰角通道:βθ1=350,βθ2=4000,βθ3=70 000,αθ1=0.5,αθ2=0.25,δθ1=0.005,δθ2=0.005,kPθ=300,kdθ=2400; 高度通道:kph=0.2,kih=0.15,kdh=0.021. 为了研究机翼折叠过程中保持初始平衡速度和高度时状态量的变化情况,给定折叠前后指令速度Vc=0.4 Ma,指令高度hc=4000 m,在50 s 的时候给定6(◦)/s 的折叠角速度,使机翼折叠60◦,得到如下仿真结果如图10 ∼图15 所示. 图10 速度变化图Fig.10 Schematic of speed change 图11 控制器作用下的高度变化图Fig.11 Schematic of height change 图12 控制器作用下的油门开度变化图Fig.12 Schematic of throttle opening change 图13 控制器作用下的舵偏角变化图Fig.13 Schematic of rudder angle change 图14 速度通道的非线性项Fig.14 Schematic of nonlinear term of the speed channel 图15 俯仰通道的非线性项跟踪Fig.15 Schematic of nonlinear term of the pitch channel 从图10 ∼图15 中可以看出,仿真初始阶段,各飞行参数会有一个较大的抖动,这是因为在初始阶段,ESO 估计的速度通道的非线性项和俯仰通道的非线性项与实际的非线性项有较大的偏差,经过反馈补偿后,相当于给系统带来了一个扰动,导致飞行参数出现了较大的抖动.从图14 和图15 中可以看出,ESO 的非线性项估计值只在仿真初始阶段与实际非线性值有一定的偏差,而后很快地跟踪上实际非线性项.在50 s 的时候,机翼开始折叠,由机翼折叠所带来的干扰项都通过ESO 进行估计补偿,故机翼折叠后,速度和高度能够保持原来的值不变.机翼折叠过程中,速度会有一个小幅度的增大,高度会有一个小幅度的减小,这是因为机翼刚开始折叠时,机翼面积减小,升力减小,无法平衡重力,故高度下降,阻力减小,推力变化较慢,故速度增大.折叠完成后,油门开度减小,舵偏角增大,这是机翼的折叠导致机翼面积和展长减小,升力和阻力减小,重新平衡时,推力减小,故油门开度减小,重力不变,为了让升力变大,故舵偏角增大. (1)基于Kane 方法建立了折叠翼飞行器的动力学模型,推导出了折叠产生的附加力和附加力矩的具体形式,便于后续动态特性分析和控制器设计. (2)对不同折叠角速度下的飞行器纵向动态响应的仿真结果表明:机翼的折叠会导致飞行速度、俯仰角和高度发生变化,折叠角速度越大,飞行器状态变化越快,变化量越小. (3) 直接针对非线性纵向动力学模型设计基于ESO 的变形稳定控制器,避免了非线性动力学模型的线性化带来的误差,简化了控制器的设计. (4)数值仿真结果表明,在所设计控制器的作用下,机翼折叠前后都能够很好地达到稳定状态,ESO能够很好地对系统总扰动进行估计.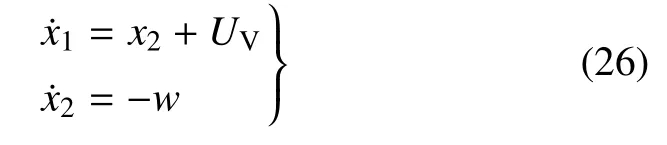




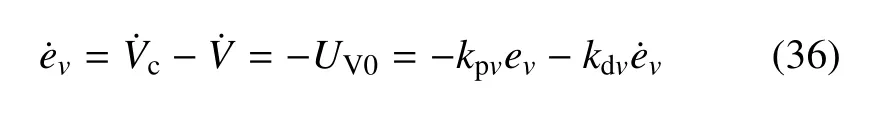
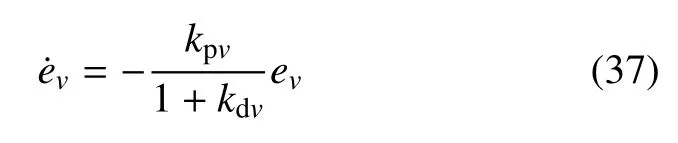

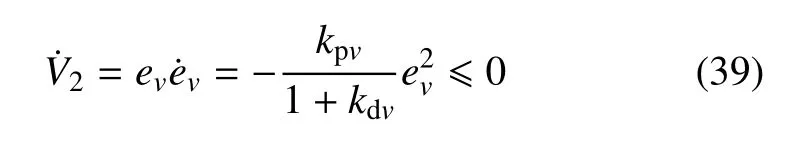
4.2 高度通道









5 仿真结果与分析






6 结论

